 13 июня 1944 года, через неделю после вторжения союзников в Нормандию, громкий жужжащий звук прогремел в небе избитого боями Лондона. Источником звука было недавно разработанное немецкое орудие войны: воздушная бомба V-1. Будучи предшественником крылатых ракет, V-1 была самоходной бомбой, управляемой с помощью гироскопов, питалась она от простого пульсирующего воздушно-реактивного двигателя, который поглощал воздух и воспламенял топливо 50 раз в секунду. Такая высокая частота пульсации давала бомбе характерный звук, зарабатывая ей прозвище «жужжащая бомба» (в оригинале – «buzz bomb» – прим. перев.).
13 июня 1944 года, через неделю после вторжения союзников в Нормандию, громкий жужжащий звук прогремел в небе избитого боями Лондона. Источником звука было недавно разработанное немецкое орудие войны: воздушная бомба V-1. Будучи предшественником крылатых ракет, V-1 была самоходной бомбой, управляемой с помощью гироскопов, питалась она от простого пульсирующего воздушно-реактивного двигателя, который поглощал воздух и воспламенял топливо 50 раз в секунду. Такая высокая частота пульсации давала бомбе характерный звук, зарабатывая ей прозвище «жужжащая бомба» (в оригинале – «buzz bomb» – прим. перев.).С июня по октябрь 1944 года немцы запустили 9521 жужжащих бомб с берегов Франции и Нидерландов, 2419 из которых достигли своих целей в Лондоне. Британцы сильно переживали насчёт реальной точности этих воздушных беспилотных летательных аппаратов. Падали ли они на город случайным образом, или всё-таки поражали намеченные цели? Действительно ли немцы разработали точные самонаводящиеся бомбы?
К счастью, они были щепетильны в поддержании статистики места и времени падения почти каждой бомбы, которая была сброшена на Лондон во время Второй мировой войны. С помощью этих данных, они могли бы статистически узнать, случайно ли падали бомбы на город или же они были точно направлены. Это был простой математический вопрос с очень важными последствиями.
Представьте себе на минуту, что вы работаете для британской разведки, и вам поставлена задача решения этой проблемы. Кто-то вручает вам бумажку с облаком точек на ней, и ваша задача выяснить – какая из моделей является случайной.
Давайте сделаем это на примере. Вот две модели из книги Стивена Пинкера «Лучшее в нас» («The better angels of our nature» в оригинале – прим. перев.). Одна из моделей генерируется случайным образом, другая имитирует рисунок с натуры. Можете ли вы сказать, что есть что?

Поразмышляли?
Вот объяснение Пинкера:
Тот, что слева (со сгустками, нитями, пустотами и волокнами) представляет собой массив, который был построен случайно – это звезды. Правый узор, в котором как кажется, отсутствует система – это строй, чьи позиции были образованы толчками друг от друга – это светлячки.
Верно – светлячки. Точки на правом рисунке указывают на позиции светлячков на потолке пещеры Waitomo в Новой Зеландии. Эти светлячки не располагаются как попало, они конкурируют за пищу и отталкиваются друг от друга. Они весьма заинтересованы не слипаться друг с другом.
Постарайтесь равномерно рассыпать песок на поверхность, и это должно выглядеть как правый рисунок. Вы инстинктивно избегаете мест, где вы уже насыпали песок. Случайные процессы не имеют таких предрассудков, песчинки просто падают где должны упасть и сгущаются вместе. Это больше похоже на россыпь песка с закрытыми глазами. Здесь ключевое отличие в том, что случайность – это не то же самое, что и единообразие. Настоящая случайность может прийти со скоплениями созвездий, которые нарисованы на ночном небе.
Вот еще один пример.
Представьте, что профессор попросил своих учеников подбросить монетку 100 раз. Один студент старательно выполнял задание и записывал результаты. Другой студент немного бездельник, и он решил подделать результаты бросков, вместо того чтобы проводить эксперимент. Можете ли вы определить, какой ученик бездельник?
Студент 1:
РОООРОРРРРОРРОРРРООРОРРОР
ОООРОРООРОРРООРРРРОРРРОРО
РРООРРРРРРРРОРОООООРОРОРО
РОРОРОООООРООРРРРРОРРООРО
Студент 2:
ОРРОРРОРООРРОРОРОРРООРОРР
ОРРОООРРОРРОРОРОРООРРОРРО
РОРОРОРОООРРОРОРОРООРОРРР
ОРООРОРОРОРООРРОРОРОРРООР
Сделайте паузу, подумайте.
Данные первого студента – длинные скопления, до восьми элементов в ряду. Удивительно, но это на самом деле то, что получается от случайных бросков монеты (я знаю – я сделал сто бросков монеты, чтобы получить такие данные!). В данных второго студента подозрительно отсутствуют скопления. На самом деле, за сто бросков монеты он не получил ряд из четырех или более орлов или решек подряд. Шанс что это когда-либо произойдёт около 0,1%.

Попытки узнать является ли набор чисел случайным, похожи на загадочные математические игры, но это не далеко от истины. Исследование случайных флуктуаций имеет свои корни во французской уголовной статистике девятнадцатого века. Франция была на пути стремительной урбанизации, плотность населения по городам начала расти, преступность и бедность стали острыми социальными проблемами.

В 1825 году Франция начала собирать статистические данные об уголовных делах, что, пожалуй, было первым случаем применения статистического анализа для изучения социальных проблем. Адольф Кетле был бельгийским математиком и одним из пионеров в области социальных наук. Его спорной целью было применять идеи вероятностей, используемые в астрономии, чтобы понять законы, которые управляют людьми.
Cо слов Майкла Мальца:
При поиске в уголовной статистике закономерности, которая была найдена в астрономических наблюдениях, он настаивал, что также как существует реальное расположение звезды, также существует реальный уровень преступности. Кетле утверждал, что у “среднего человека” была статистически постоянная “склонность к преступлению”, что позволило бы создать “социальную физику”.
Кетле заметил, что количество обвинительных приговоров медленно падало с течением времени, и сделал вывод, что имеет место тенденция к снижению “склонности к преступлению” у французских граждан. Были некоторые проблемы с данными, которые он использовал, но основные ошибки в его методе были раскрыты гениальным французским эрудитом и ученым Симеоном Дени Пуассоном.

Идея Пуассона была гениальной и на удивление современной. Говоря на современном языке, он утверждал, что Кетле не хватало модели для его данных, он не объяснял, как на самом деле присяжные пришли к своим решениям. По Пуассону, присяжные просто ошибались. Данные, которые мы наблюдаем – об изменении убеждений, но то, что мы хотим знать – это вероятность того, что подсудимый виновен. Эти две величины не то же самое, но они могут быть связаны. В итоге, когда мы берём весь процесс во внимание, появляется определенное количество переменных присущих обвинительным приговорам, и результат этого – то, что мы видим в уголовной статистике Франции.
В 1837 году Пуассон опубликовал этот результат в труде “Исследования теории вероятностей судебных решений по уголовным и гражданским делам”. В этой работе он ввел формулу, которую мы теперь называем распределением Пуассона. Она объясняет нам как шансы большого числа редких событий превращаются в конкретный результат (как большая часть французских присяжных принимает неправильное решение). Предположим, что в среднем 45 человек в год ударяет молнией. Подставьте это в формулу Пуассона наряду с численностью населения, и она будет выдавать какова вероятность того, что 10 человек в год будет поражено молнией, или 50, или 100. Предполагается, что удары молнии являются независимыми, редкими событиями, которые так же могут произойти в любое время. Иными словами, формула Пуассона может показать вам, какова вероятность получить редкое событие случайным образом.

Одно из первых применений формулы Пуассона пришло из маловероятного места. Прыгаем на шестьдесят лет вперед, через франко-прусскую войну, и оказываемся в 1898 году в Пруссии. Владислав Борткевич, русский статистик польского происхождения, пытался понять, почему в некоторые годы необычно большое количество солдат в прусской армии погибали под копытами лошадей. Иногда в одном подразделении было 4 таких смерти в течение одного года. Было ли это просто совпадением?
Постоянная частота смерти от удара лошади маловероятна. Борткевич понял, что он мог бы использовать формулу Пуассона, чтобы узнать сколько смертей мы предполагаем увидеть. Вот предсказание, в сравнении с реальными данными.
| Количество смертей от удара лошади | Предсказанные случаи по Пуассону | Наблюдаемые случаи |
|---|---|---|
| 0 | 108.67 | 109 |
| 1 | 66.29 | 65 |
| 2 | 20.22 | 22 |
| 3 | 4.11 | 3 |
| 4 | 0.63 | 1 |
| 5 | 0.08 | 0 |
| 6 | 0.01 | 0 |
Видите, как хорошо они сочетаются? Скопления связанных с лошадьми смертей – это то, что можно было бы ожидать, если бы мы считали лошадиные удары копытами чисто случайным процессом. Случайность приходит со скоплениями.
Я решил проверить это самостоятельно. Я поискал общественно доступные данные о смертях по причине редких событий, и наткнулся на «Международный файл акульих атак», который подсчитывает случаи нападений акул на людей по всему миру. Вот данные о случаях нападений акул в Южной Африке.
| Year | Number of Shark Attacks in South Africa |
|---|---|
| 2000 | 4 |
| 2001 | 3 |
| 2002 | 3 |
| 2003 | 2 |
| 2004 | 5 |
| 2005 | 4 |
| 2006 | 4 |
| 2007 | 2 |
| 2008 | 0 |
| 2009 | 6 |
| 2010 | 7 |
| 2011 | 5 |
Эти цифры достаточно малы, в среднем 3,75. Но сравним 2008 и 2009 годы. В один год было 0 нападений акул, а на следующий целых 6. И в 2010 их было 7. Вы уже можете представить себе как заголовки кричат: «Акулы нападают!». Но на самом ли деле это восстание акул? Чтобы выяснить это, я сравнил данные прогноза г-на Пуассона.

По горизонтали указано количество нападений, а по вертикали – количество лет. Например, самый длинный синий столбик указывает на то, что 3 года было 4 нападения (2000, 2005 и 2006). Красная пунктирная линия – это распределение Пуассона, и она представляет собой результаты, которые можно было бы ожидать, если принять нападение акул как чисто случайный процесс. Это хорошо соответствует данным, и я боюсь, что это исключает большое южно-африканское восстание акул 2010 года. Урок опять же, в том, что случайность не означает единообразие.
И что возвращает нас к «жужжащим» бомбам. Вот визуализация количества бомб, сброшенных над различными частями города:
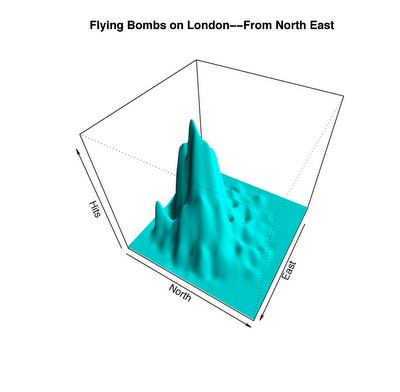
Это далеко от равномерного распределения, но является ли это свидетельством точного нацеливания? На данный момент, вы можете догадаться как ответить на этот вопрос. В докладе, под названием «применение распределения Пуассона», британский статистик имени Р.Д. Кларк написал:
Во время воздушной бомбардировки на Лондон ходило мнение, что точки нацеливания бомб, как правило, образуют скопления. Поэтому было решено применить статистический тест, чтобы выяснить насколько это утверждение корректно.
Кларк взял район площадью 12 км х 12 км, который сильно подвергся бомбардировке, и разделил его сеткой. В итоге у него получилось 576 квадратов, каждый размером в 25 городских кварталов. Затем он подсчитал число квадратов с 0 сброшенных бомб, с 1ой сброшенной бомбой, с 2мя и так далее.
Всего 537 бомб упали на эти 576 квадратов. Это около одной бомбы на квадрат в среднем. Он подставил эти числа в формулу Пуассона, чтобы узнать сколько скоплений ожидается получить случайным образом. Вот соответствующая таблица из его статьи:

Сравните две колонки, и вы можете увидеть как невероятно точно предсказание соответствует реальности. Есть 7 квадратов, которые пострадали от 4-х бомб каждый – это то, что вы бы ожидали ввиду случайности. В большую часть Лондона бомбы не угодили. Они обрушились наугад, в разрушительной общегородской игре в Русскую рулетку.
Распределение Пуассона имеет привычку подкрадываться во всевозможных местах, в некоторых случаях несущественно, а в других изменяя вашу жизнь. Число мутаций в ДНК и возраст ваших клеток; количество автомобилей перед вами на светофоре, или пациентов в очереди перед вами в отделение неотложной помощи; количество опечаток в каждом из моих постов в блоге; число пациентов с лейкемией в данном городе; число рождений и смертей, браков и разводов, или самоубийств и убийств в данном году; количество блох на вашей собаке.
Эти викторианские ученые научили нас, что от мирских моментов к вопросам жизни и смерти, случайность играет более сильную роль в нашей жизни, чем мы готовы признать. К сожалению, этот факт не придаёт утешения, когда карты в водопаде жизни розданы не в нашу пользу.
«Так много жизни, мне кажется, определяется чистой случайностью.» — Сидни Пуатье