Эта статья — продолжение первой части. В этой серии статей я рассматриваю применение набирающего популярность языка программирования R для решения распространенных статистических задач.
В данной и следующей статье я показываю как выбрать для обработки качественных и количественных данных правильные тесты и реализовать их в R. Данные методы позволяют получить реальное представление об объекте, процессе или явлении по какому-либо параметру, т.е. позволяют сказать «хорошо» или «плохо». Они не потребуют глубоких знаний программирования и статистики, и пригодятся людям различного рода деятельности.
Заинтересовались? Добро пожаловать под кат!
Часть 1: Бинарная классификация
Часть 3: Тесты количественных данных
Перед тем как начать, сделаю важное замечание. Самое сложное, выбрать, как анализировать данные. R — это инструмент, он сделает все, что вы ему скажете. Но если вы примените не тот метод, ваши результаты не будут иметь смысла.
Тестирование применяется для того, чтобы сравнить две случайные величины, т.е. доказать наличие или отсутствие разницы между ними. Основная идея в том, что происходит сопоставление разницы средних значений и стандартного отклонения.
В статистике оперируют так называемыми гитпотезами. Их всего две. Основная, H0, что отличия нет:

Альтернативная, H1, отличие величин:
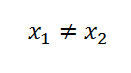
Гипотеза может быть и вида x1<x2, и тогда вам придется использовать односторонние тесты. Но на практике это делается крайне редко.
Также необходимо задать ошибку первого рода, α. Я упоминал ее в прошлой статье, как (1 — чувствительность) для биноминальной классификации. Это ошибка, с которой мы предсказываем H1. Стандартной α являетя 5%.
Каждый тест на выходе дает 2 значения: тест-статистику и p-значение, что по сути одно и тоже. Кратко объясню что это. Как мы знаем, доверительный интервал (т.е. интервал, в котором случайная величина находится с заданой вероятностью), который мы будет составлять для H0, представляется формулой:
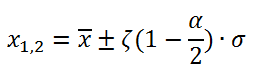
где x — среднее значение, σ — стандартное отклонение.
ζ — это квантиль используемого распределения, т.е. множитель, который соответствует интервалу заданной вероятности. α — ошибка первого рода, т.е. вероятность, что x окажется за пределами интервала.
В тесте имеется значение x альтернативной гипотезы. Тест-статистика характеризует его в размерности квантиля, а p-значение в размерности вероятности. Если p-значение меньше, чем α, либо тест-статистика больше квантиля, то альтернативная гипотеза находится за пределами этого интервала. В этом случае, c вероятностью ошибки alpha, мы принимаем H1, т.к. считаем, что тестируемое значение не может относиться к H0. Тест-статистика и p-значение являются результатами теста.
Если мы построим доверительный интервал, то получим по сути тоже самое. Возможно, многим это будет естественнее. Тем не менее, тесты устроены по принципу p-значения, давайте ими пользоваться и не задумываться на концептуальном уровне (тем более люди этим всю жизнь занимались, видимо, нужно именно так).
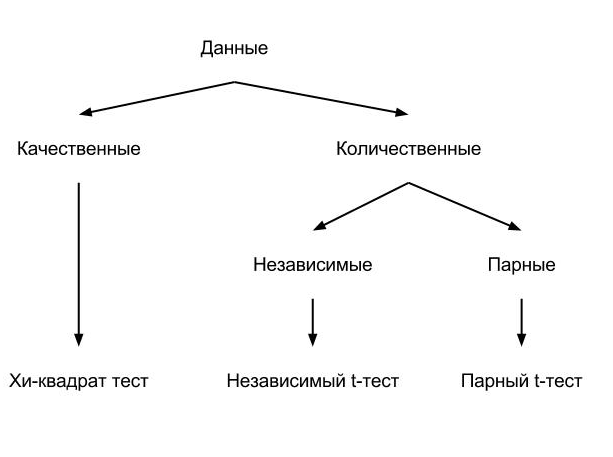
Данные являются парными, если оба значения получены с одного объекта. Например, сравнение результатов “до и после” или использование двух алгоритмов на одних данных. Однозначно, что парный тест менее строгий, т.е. эффект можно доказать при меньшей выборке.
Вы определили с чем имеете дело. Что делать дальше. Вот некоторый алгоритм работы.
Качественные данные это “да” и “нет”. Примеры применения: сравнение работы двух методик/алгоритмов/отделов компаний, нахожение влияния наличия антивируса на заражение компьютера/курения на рак легих/текста рекламы на факт продажи. Для этих данных работает биноминальное распределение.
Для примера я взял несколько абстрактные бинарные данные, две группы по 25 элементов. Каждый элемент это 0 или 1. Будем работать с ними, как я указал выше: сперва красиво представим эти данные (возможно после этого никакие тесты будут не нужны), затем будем проводить анализ.
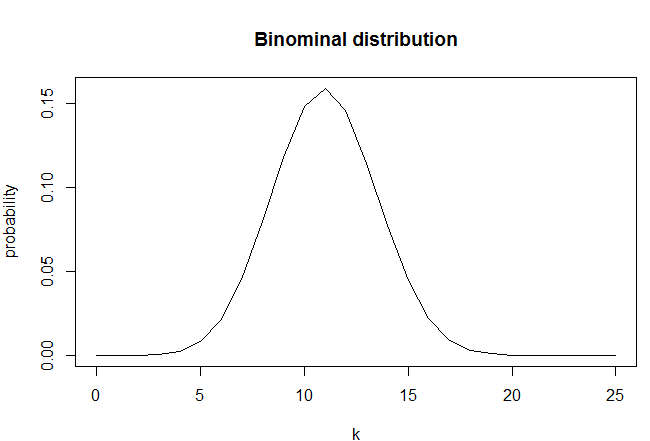
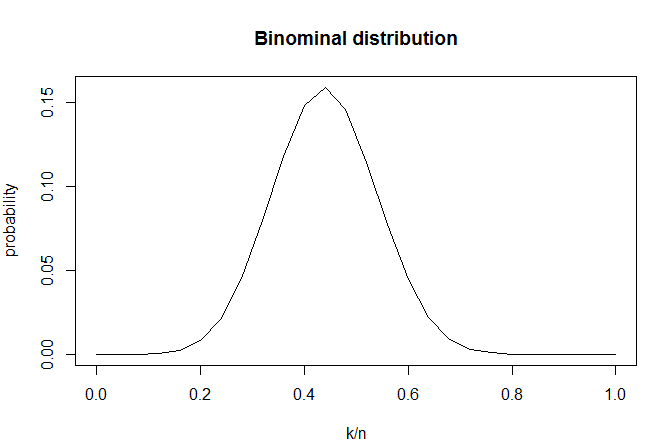
Для примера, построим биноминальное распределение для первой выборки, полагая, что значение вероятности является истинным. Таким образом, мы получим, как на основании имеющихся данных должна себя вести случайная величина.
Если нам интересна вероятность:
Для описания данных нужно предстивить среднюю веоятность с доверительным интервалом для каждой группы. Функция плотности вероятности выглядит следующим образом:
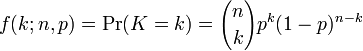
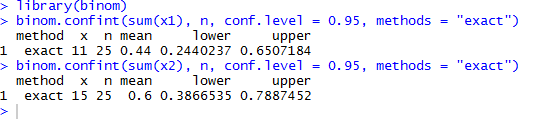
В R нам поможет билиотека binom. Установив ее, используем код:
Уже сейчас можно сделать вывод, что хотя разница средних значений существенна, доверительные интервалы пересекаются, что в целом было ожидаемо для таких маленьких выборок. Также отмечу, что если бы вы считали по выше приведенной формуле, то получили другие результаты. В данном расчете используется точный метод, в то время как формула являтся приближенной. Разница уменьшается с увеличением выборки.
Хи-квадрат тест используется для анализа нескольких биноминальных выборок. Он распространен, т.к. его легко провести руками.

Нам выдали предупреждение. Дело в том, что хи-квадрат тест является приближенным (хотя даже тут R использует дополнительную коррекцию, ее можно отключить, если нужно). Для маленьких выборок он дает ошибку. Существует более сложный, но абсолютно точный тест, учитывающий неизвестность некоторых параметров, неучтенную в хи-квадрат тесте. Это тест Фишера.

P-значение 9.915%, что больше, чем 5%. Поэтому оставляем гипотезу H0 — разницы между величинами нет.
Для этих тестов можно брать несколько групп. В этом случае H1 будет отражать отличие хотя бы одной группы от других.
На этом я завершаю эту статью. Сегодня я рассказал о том, как использовать тесты, как выбрать подходящий тест, а также подробно разобрал анализ качественных данных, применение хи-квадрат теста и теста Фишера. Текста было больше, чем R, но никуда не деться. В следующей, я перейду к анализу количественных выборок.
Файлы примера
P.S. Жду правок, дополнений и альтернативных точек зрения в комментариях.
В данной и следующей статье я показываю как выбрать для обработки качественных и количественных данных правильные тесты и реализовать их в R. Данные методы позволяют получить реальное представление об объекте, процессе или явлении по какому-либо параметру, т.е. позволяют сказать «хорошо» или «плохо». Они не потребуют глубоких знаний программирования и статистики, и пригодятся людям различного рода деятельности.
Заинтересовались? Добро пожаловать под кат!
Часть 1: Бинарная классификация
Часть 3: Тесты количественных данных
Перед тем как начать, сделаю важное замечание. Самое сложное, выбрать, как анализировать данные. R — это инструмент, он сделает все, что вы ему скажете. Но если вы примените не тот метод, ваши результаты не будут иметь смысла.
Немного теории
Тестирование применяется для того, чтобы сравнить две случайные величины, т.е. доказать наличие или отсутствие разницы между ними. Основная идея в том, что происходит сопоставление разницы средних значений и стандартного отклонения.
В статистике оперируют так называемыми гитпотезами. Их всего две. Основная, H0, что отличия нет:

Альтернативная, H1, отличие величин:

Гипотеза может быть и вида x1<x2, и тогда вам придется использовать односторонние тесты. Но на практике это делается крайне редко.
Также необходимо задать ошибку первого рода, α. Я упоминал ее в прошлой статье, как (1 — чувствительность) для биноминальной классификации. Это ошибка, с которой мы предсказываем H1. Стандартной α являетя 5%.
Каждый тест на выходе дает 2 значения: тест-статистику и p-значение, что по сути одно и тоже. Кратко объясню что это. Как мы знаем, доверительный интервал (т.е. интервал, в котором случайная величина находится с заданой вероятностью), который мы будет составлять для H0, представляется формулой:

где x — среднее значение, σ — стандартное отклонение.
ζ — это квантиль используемого распределения, т.е. множитель, который соответствует интервалу заданной вероятности. α — ошибка первого рода, т.е. вероятность, что x окажется за пределами интервала.
В тесте имеется значение x альтернативной гипотезы. Тест-статистика характеризует его в размерности квантиля, а p-значение в размерности вероятности. Если p-значение меньше, чем α, либо тест-статистика больше квантиля, то альтернативная гипотеза находится за пределами этого интервала. В этом случае, c вероятностью ошибки alpha, мы принимаем H1, т.к. считаем, что тестируемое значение не может относиться к H0. Тест-статистика и p-значение являются результатами теста.
Если мы построим доверительный интервал, то получим по сути тоже самое. Возможно, многим это будет естественнее. Тем не менее, тесты устроены по принципу p-значения, давайте ими пользоваться и не задумываться на концептуальном уровне (тем более люди этим всю жизнь занимались, видимо, нужно именно так).
Выбор методики

Данные являются парными, если оба значения получены с одного объекта. Например, сравнение результатов “до и после” или использование двух алгоритмов на одних данных. Однозначно, что парный тест менее строгий, т.е. эффект можно доказать при меньшей выборке.
Этапы работы с данными
Вы определили с чем имеете дело. Что делать дальше. Вот некоторый алгоритм работы.
- Описание. Получить средние значения, среднеквадратичные отклонения, пострить графики распределения
- Принятие решения
- Соответствующий тест
- Получение доверительного интервала (в R включено в тесты)
Обработка качественных данных
Качественные данные это “да” и “нет”. Примеры применения: сравнение работы двух методик/алгоритмов/отделов компаний, нахожение влияния наличия антивируса на заражение компьютера/курения на рак легих/текста рекламы на факт продажи. Для этих данных работает биноминальное распределение.
Для примера я взял несколько абстрактные бинарные данные, две группы по 25 элементов. Каждый элемент это 0 или 1. Будем работать с ними, как я указал выше: сперва красиво представим эти данные (возможно после этого никакие тесты будут не нужны), затем будем проводить анализ.
Для примера, построим биноминальное распределение для первой выборки, полагая, что значение вероятности является истинным. Таким образом, мы получим, как на основании имеющихся данных должна себя вести случайная величина.
tab <- read.csv(file="data1.csv", header=TRUE, sep=",", dec=".")
attach(tab)
tab
x1 <- X[Group==1]
x2 <- X[Group==2]
library(graphics)
n <- length(x1)
p1 <- mean(x1)
k <- seq(0, n, by = 1)
plot (k, dbinom(k, n, p), type = "l", ylab = "probability",
main = "Binominal distribution")

Если нам интересна вероятность:
plot (k/n, dbinom(k, n, p), type = "l", ylab = "probability",
main = "Binominal distribution")

Для описания данных нужно предстивить среднюю веоятность с доверительным интервалом для каждой группы. Функция плотности вероятности выглядит следующим образом:

В R нам поможет билиотека binom. Установив ее, используем код:
library(binom)
binom.confint(sum(x1), n, conf.level = 0.95, methods = "exact")
binom.confint(sum(x2), n, conf.level = 0.95, methods = "exact")

Уже сейчас можно сделать вывод, что хотя разница средних значений существенна, доверительные интервалы пересекаются, что в целом было ожидаемо для таких маленьких выборок. Также отмечу, что если бы вы считали по выше приведенной формуле, то получили другие результаты. В данном расчете используется точный метод, в то время как формула являтся приближенной. Разница уменьшается с увеличением выборки.
Хи-квадрат тест используется для анализа нескольких биноминальных выборок. Он распространен, т.к. его легко провести руками.
chisq.test(x1,x2)

Нам выдали предупреждение. Дело в том, что хи-квадрат тест является приближенным (хотя даже тут R использует дополнительную коррекцию, ее можно отключить, если нужно). Для маленьких выборок он дает ошибку. Существует более сложный, но абсолютно точный тест, учитывающий неизвестность некоторых параметров, неучтенную в хи-квадрат тесте. Это тест Фишера.
fisher.test(x1, x2)

P-значение 9.915%, что больше, чем 5%. Поэтому оставляем гипотезу H0 — разницы между величинами нет.
Для этих тестов можно брать несколько групп. В этом случае H1 будет отражать отличие хотя бы одной группы от других.
Итоги
На этом я завершаю эту статью. Сегодня я рассказал о том, как использовать тесты, как выбрать подходящий тест, а также подробно разобрал анализ качественных данных, применение хи-квадрат теста и теста Фишера. Текста было больше, чем R, но никуда не деться. В следующей, я перейду к анализу количественных выборок.
Файлы примера
P.S. Жду правок, дополнений и альтернативных точек зрения в комментариях.