От автора
Данная статья рассматривает один из алгоритмов сортировки массивов. Она предназначена для новичков или же для тех кто по каким-то причинам не знаком с данным алгоритмом. Исправления и поправки только приветствуются:)
Теория
Сортировка вставками (Insertion Sort) — это простой алгоритм сортировки. Суть его заключается в том что, на каждом шаге алгоритма мы берем один из элементов массива, находим позицию для вставки и вставляем. Стоит отметить что массив из 1-го элемента считается отсортированным.
Словесное описание алгоритма звучит довольно сложно, но на деле это самая простая в реализации сортировка. Каждый из нас, не зависимо от рода деятельности, применял алгоритм сортировки, просто не осознавал это:) Например когда сортировали купюры в кошельке — берем 100 рублей и смотрим — идут 10, 50 и 500 рублёвые купюры. Вот как раз между 50 и 500 и вставляем нашу сотню:) Или приведу пример из всех книжек — игра в карточного «Дурака». Когда мы тянем карту из колоды, смотрим на наши разложенные по возрастанию карты и в зависимости от достоинства вытянутой карты помещаем карту в соответствующее место. Для большей наглядности приведу анимацию из википедии.
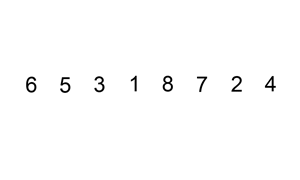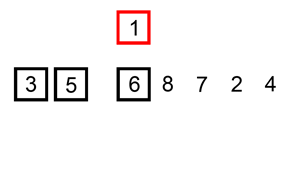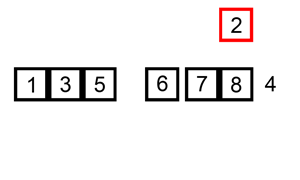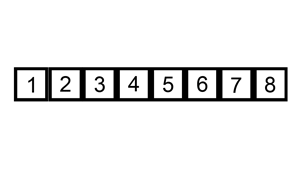
Реализация
Прежде чем приступить к реализации определимся с форматом входных данных — для примера это будет массив целочисленных (int) значений. Нумерация элементов массива начинается с 0 и заканчивается n-1. Сам алгоритм реализуем на языке C++. Итак приступим…
Основной цикл алгоритма начинается не с 0-го элемента а с 1-го, потому что элемент до 1-го элемента будет нашей отсортированной последовательностью (помним что массив состоящий из одного элемента является отсортированным) и уже относительно этого элемента с номером 0 мы будем вставлять все остальные. Собственно код:
Реализация сортировки очень проста, всего 3 строчки. Функция swap меняет местами элементы x[j-1] и x[j]. Вложенный цикл ищет место для вставки. Рекомендую запомнить этот алгоритм, чтобы в случае необходимости написать сортировку не позориться сортировкой пузырьком:)
Анализ производительности
Сортировка вставками имеет сложность n2, количество сравнений вычисляется по формуле n*(n-1)/2. Для доказательства был написан следующий код:
Количество перестановок для 100 элементов:
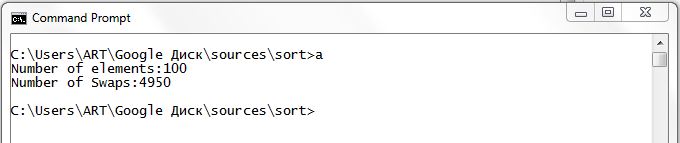
Итак при n=100 количество перестановок равно 4950, а не 10000 если бы мы высчитывали по формуле n2. Имейте это ввиду при выборе алгоритма сортировки.
Эффективность
Сортировка вставками наиболее эффективна когда массив уже частично отсортирован и когда элементов массива не много. Если же элементов меньше 10 то данный алгоритм является лучшим. Не зря в быстрой сортировке (оптимизация Боба Седжвика) используется алгоритм сортировки вставками как вспомогательный, но об этом алгоритме мы поговорим позже…
Данная статья рассматривает один из алгоритмов сортировки массивов. Она предназначена для новичков или же для тех кто по каким-то причинам не знаком с данным алгоритмом. Исправления и поправки только приветствуются:)
Теория
Сортировка вставками (Insertion Sort) — это простой алгоритм сортировки. Суть его заключается в том что, на каждом шаге алгоритма мы берем один из элементов массива, находим позицию для вставки и вставляем. Стоит отметить что массив из 1-го элемента считается отсортированным.
Словесное описание алгоритма звучит довольно сложно, но на деле это самая простая в реализации сортировка. Каждый из нас, не зависимо от рода деятельности, применял алгоритм сортировки, просто не осознавал это:) Например когда сортировали купюры в кошельке — берем 100 рублей и смотрим — идут 10, 50 и 500 рублёвые купюры. Вот как раз между 50 и 500 и вставляем нашу сотню:) Или приведу пример из всех книжек — игра в карточного «Дурака». Когда мы тянем карту из колоды, смотрим на наши разложенные по возрастанию карты и в зависимости от достоинства вытянутой карты помещаем карту в соответствующее место. Для большей наглядности приведу анимацию из википедии.
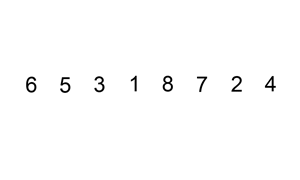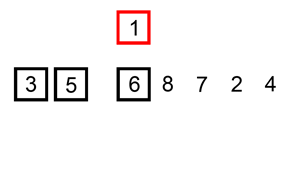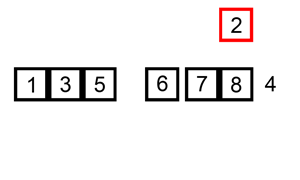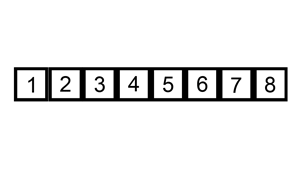
Реализация
Прежде чем приступить к реализации определимся с форматом входных данных — для примера это будет массив целочисленных (int) значений. Нумерация элементов массива начинается с 0 и заканчивается n-1. Сам алгоритм реализуем на языке C++. Итак приступим…
Основной цикл алгоритма начинается не с 0-го элемента а с 1-го, потому что элемент до 1-го элемента будет нашей отсортированной последовательностью (помним что массив состоящий из одного элемента является отсортированным) и уже относительно этого элемента с номером 0 мы будем вставлять все остальные. Собственно код:
for(int i=1;i<n;i++)
for(int j=i;j>0 && x[j-1]>x[j];j--) // пока j>0 и элемент j-1 > j, x-массив int
swap(x[j-1],x[j]); // меняем местами элементы j и j-1
Реализация сортировки очень проста, всего 3 строчки. Функция swap меняет местами элементы x[j-1] и x[j]. Вложенный цикл ищет место для вставки. Рекомендую запомнить этот алгоритм, чтобы в случае необходимости написать сортировку не позориться сортировкой пузырьком:)
Анализ производительности
Сортировка вставками имеет сложность n2, количество сравнений вычисляется по формуле n*(n-1)/2. Для доказательства был написан следующий код:
void Sort(int* arr,int n){
int counter=0;
for(int i=1;i<n;i++){
for(int j=i; j>0 && arr[j-1]>arr[j];j--){
counter++;
int tmp=arr[j-1];
arr[j-1]=arr[j];
arr[j]=tmp;
}
}
cout<<counter<<endl;
}
Количество перестановок для 100 элементов:

Итак при n=100 количество перестановок равно 4950, а не 10000 если бы мы высчитывали по формуле n2. Имейте это ввиду при выборе алгоритма сортировки.
Эффективность
Сортировка вставками наиболее эффективна когда массив уже частично отсортирован и когда элементов массива не много. Если же элементов меньше 10 то данный алгоритм является лучшим. Не зря в быстрой сортировке (оптимизация Боба Седжвика) используется алгоритм сортировки вставками как вспомогательный, но об этом алгоритме мы поговорим позже…