
Отгадайте загадку: в четырёх измерениях сидит и комплексными числами воротит?
Подсказка: это вектор со скаляром. И вещественная матрица. И придумал его Гамильтон.
Не помогло? Ну что вы, это же элементарно! Это кватернион! Кватернионы используют для записи вращений в робототехнике, игровых движках, ПО для моделирования и вообще везде, где не нужны проблемы с углами Эйлера или матрицами. Если вас испугала путаница выше с разными представлениями кватерниона, то можете быть спокойны. Кватернионы очень просты в использовании и их внутреннее строение может понадобиться только в очень редких случаях, где нужна тонкая оптимизация. В остальное время с помощью кватернионов можно крутить всё что угодно и как угодно, и оно будет плавно и красиво интерполироваться без шарнирных замков.
Что же такое кватернион? Понять его проще всего, если разделить на две части: вектор и вращение вокруг него. Представьте, что вы внутри сферы. Вы можете протянуть руку и коснуться внутренней поверхности сферы. Это будет вектор. Теперь, если поворотом кисти вы будете вращать сферу, то получится второй компонент кватерниона. Кватернион это конечное вращение, которое получается из исходного положения.
Кватернион имеет хитрое внутреннее строение. Его можно записать с помощью четырёх чисел: x, y, z для вектора и w для поворота. Сложность заключается в том, что в дополнение к ним ещё есть три мнимые единицы, такие, что: i2 = j2 = k2 = ijk = −1. Целиком запись выглядит следующим образом: q = w + x*i + y*j + z*k
Из-за единиц сложение-умножение кватернионов вручную достаточно муторно, но, к счастью, в программировании они не особо важны. Все операции обычно производятся над кватернионами в целом, и лишь изредка используются те четыре числа. Кроме того, во многих библиотеках имеются специальные конструкторы, которые позволяют получить кватернион из более понятных структур, например Quaternion.Euler в Unity3d или Quaternion.CreateFromYawPitchRoll в XNA.
В работе с кватернионами чаще всего приходится их умножать друг на друга. Это очень полезная операция, ведь при умножении одного кватерниона на другой получается первое вращение, повёрнутое на второе. Важно помнить, что умножение кватернионов некоммутативно, а значит важен порядок операндов. То есть q1*q2 это не то же самое, что и q2*q1. На картинке ниже можете посмотреть на разницу. Слева: Quaternion.Euler(60, 0, 60) * Quaternion.Euler(0, 60, 0), справа: Quaternion.Euler(0, 60, 0) * Quaternion.Euler(60, 0, 60). Цветными линиями показаны пути локальных осей каждого самолётика.
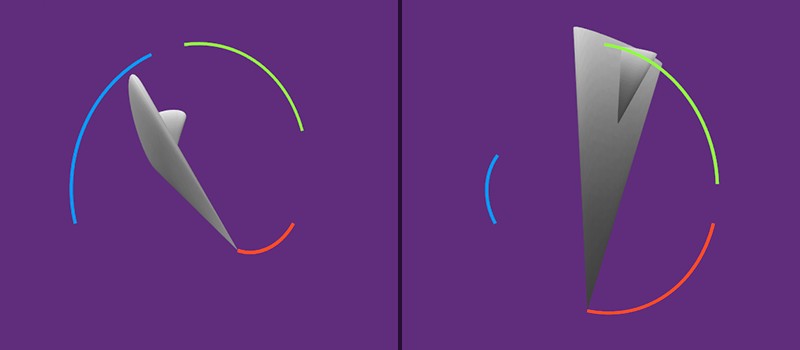
На практике работа с кватернионами выглядит так:
var rightTurn = Quaternion.Euler(0, 90, 0); // Создаём новый поворот направо
car.rotation = car.rotation*rightTurn; // Крутим
В примере выше машинка car поворачивается направо в локальных координатах. Если машина едет по наклонной плоскости, или даже вверх ногами, то она всё равно корректно повернётся куда нужно. Переменную rightTurn можно использовать любое количество раз, вот так, например, выглядит поворот на 360 градусов:
car.rotation = car.rotation*rightTurn*rightTurn*rightTurn*rightTurn;
По умолчанию кватернион использует глобальные оси координат для отсчёта вращения. Когда один кватернион умножают на другой кватернион, то для второго кватерниона точкой отсчёта становится первый кватернион.
Если бы вы вдруг захотели смоделировать перемещение по разнообразным выпуклым поверхностям как в Super Mario Galaxy с помощью углов Эйлера, то вам пришлось бы долго ломать голову. Всё потому, что они были придуманы для указания конкретной ориентации объекта в пространстве, а не для анимации. С кватернионами всё гораздо проще, и они замечательно интерполируются по кратчайшим путям, тогда как углы Эйлера начинают юлить из-за иерархии поворотов и частенько застревают в шарнирном замке, про который я писал в этой статье. На анимации ниже можете посмотреть как сильно отличается их сферическая интерполяция. Слева кватернионы, справа углы Эйлера.

Если вам всё-таки интересно как кватернионы выглядят внутри, то можете посмотреть на таблицу ниже.
| w | x | y | z | Вращение |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | нет вращения |
| 0 | 1 | 0 | 0 | 180° вокруг оси X |
| sqrt(0.5) | sqrt(0.5) | 0 | 0 | 90° вокруг оси X |
| sqrt(0.5) | -sqrt(0.5) | 0 | 0 | -90° вокруг оси X |
Значения в таблице получаются из следующей формулы:
[w, x, y, z] = [cos(alpha/2), sin(alpha/2)*vx, sin(alpha/2)*vy, sin(alpha/2)*vz]
Где alpha — это угол вращения, а vx, vy, vz — вектор оси вращения.
Результатом сложения кватернионов является промежуточное вращение. Сложение кватернионов элементарно, достаточно просто сложить их компоненты. Возьмём, например, q1 = 1 + 0i + 0j + 0k (нулевое вращение из таблицы выше) и q2 = 0 + 1i + 0j + 0k (180° вокруг оси X). Их суммой будет q3 = 1 + 1i + 0j + 0k, т. е. 90° вокруг оси X. К сожалению, в Unity3d оператор сложения не реализован для кватернионов.
Если вы хотите узнать побольше о кватернионах, то советую начать с английской Википедии. Также можете покопаться в Wolfram|Alpha, он выдаёт тонны попутной информации и вообще много умеет. Также можете посмотреть на разницу между углами Эйлера и кватернионами в интерактивной демонстрации по ссылкам ниже.
Видео
WebGL | Windows | Linux | Mac | Исходники на GitHub
Мышкой вращать сцену, AD, WS и QE — вращение вокруг осей, Esc — выход, остальные кнопки указаны на экране.
Для пользователей Linux: Сделайте файл Quaternions исполняемым с помощью «chmod +x Quaternions» и запускайте.