Эта статья рассказывает о времени выполнения и о расходе памяти большинства алгоритмов используемых в информатике. В прошлом, когда я готовился к прохождению собеседования я потратил много времени исследуя интернет для поиска информации о лучшем, среднем и худшем случае работы алгоритмов поиска и сортировки, чтобы заданный вопрос на собеседовании не поставил меня в тупик. За последние несколько лет я проходил интервью в нескольких стартапах из Силиконовой долины, а также в некоторых крупных компаниях таких как Yahoo, eBay, LinkedIn и Google и каждый раз, когда я готовился к интервью, я подумал: «Почему никто не создал хорошую шпаргалку по асимптотической сложности алгоритмов? ». Чтобы сохранить ваше время я создал такую шпаргалку. Наслаждайтесь!

Пусть дан граф с |V| вершинами и |E| ребрами, тогда


Короче говоря, если алгоритм имеет сложность __ тогда его эффективность __


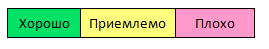
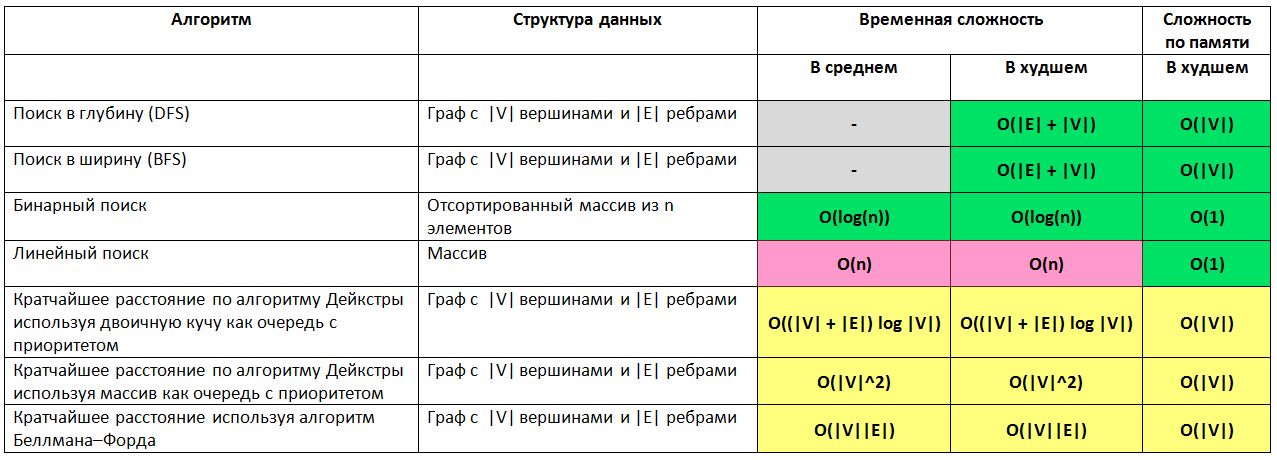
Поиск
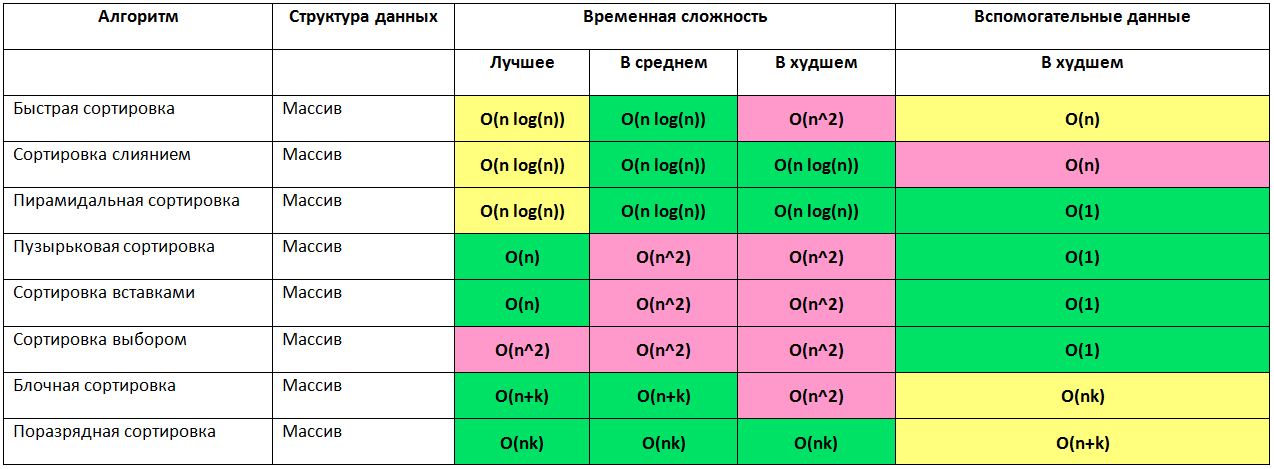
Сортировка

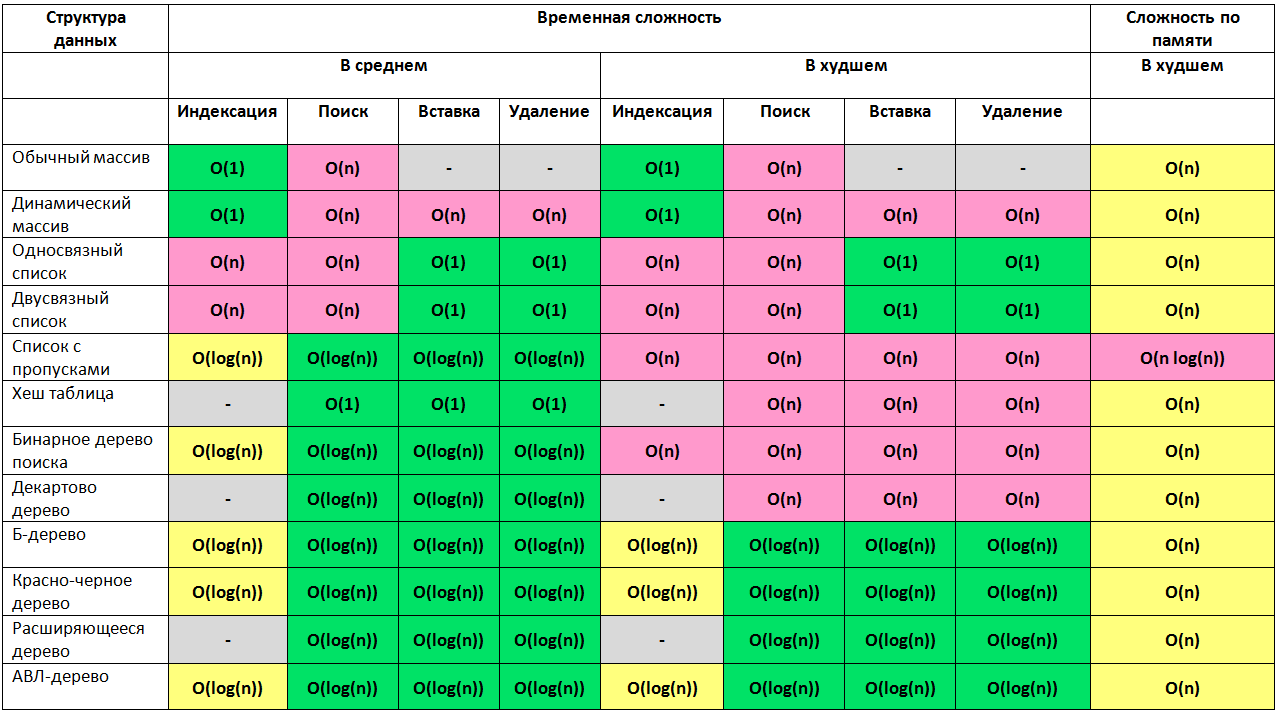
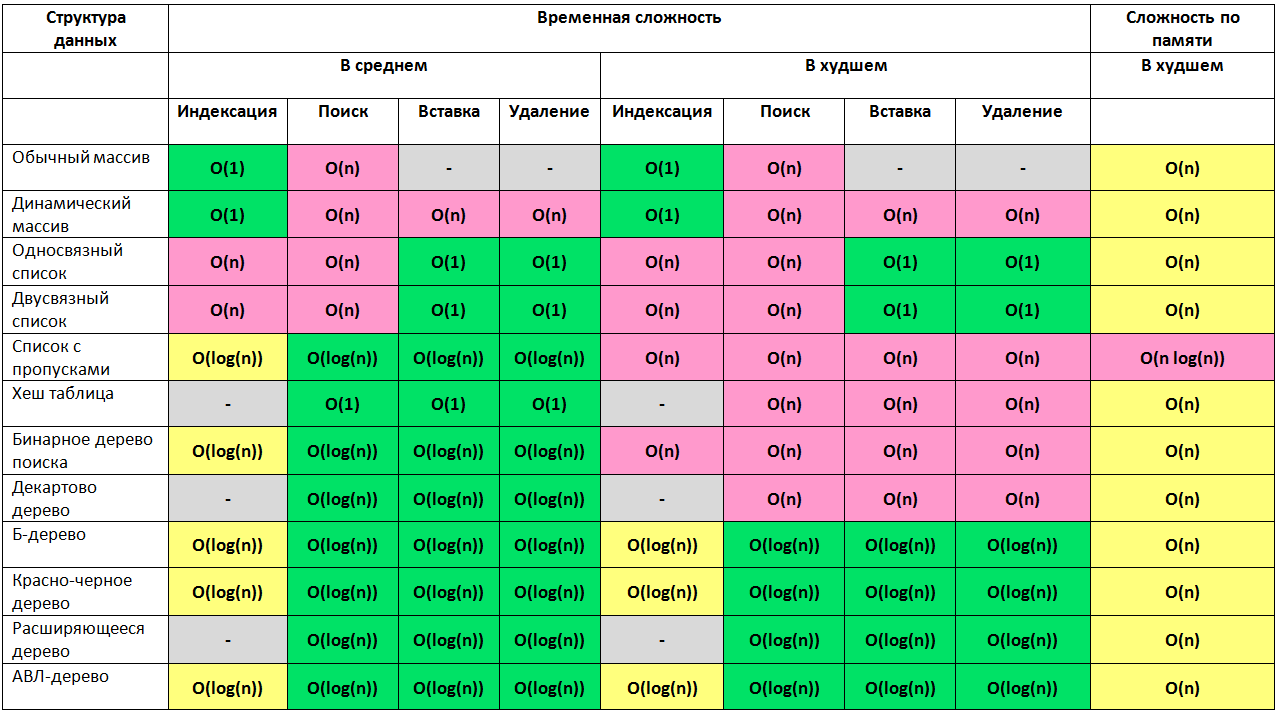
Структуры данных
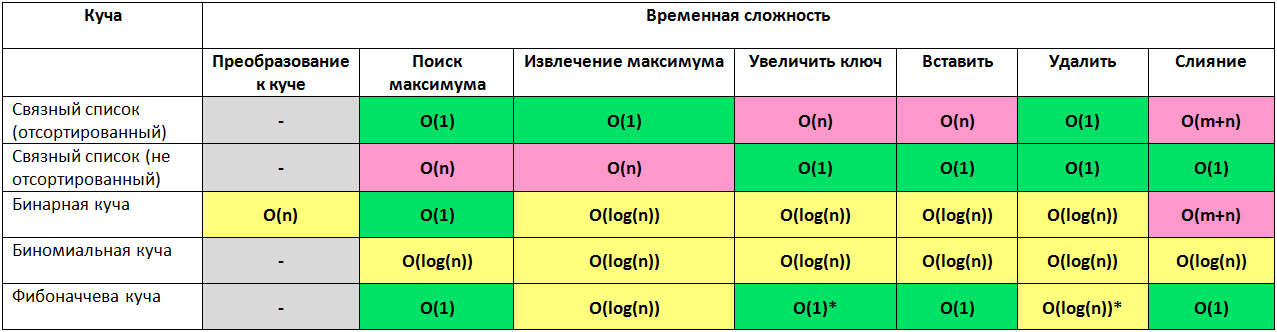
Кучи
Представление графов
Пусть дан граф с |V| вершинами и |E| ребрами, тогда

Нотация асимптотического роста
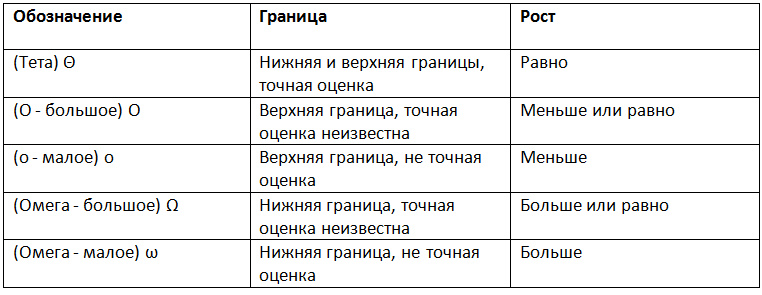
- (О — большое) — верхняя граница, в то время как (Омега — большое) — нижняя граница. Тета требует как (О — большое), так и (Омега — большое), поэтому она является точной оценкой (она должна быть ограничена как сверху, так и снизу). К примеру, алгоритм требующий Ω (n logn) требует не менее n logn времени, но верхняя граница не известна. Алгоритм требующий Θ (n logn) предпочтительнее потому, что он требует не менее n logn (Ω (n logn)) и не более чем n logn (O(n logn)).
- f(x)=Θ(g(n)) означает, что f растет так же как и g когда n стремится к бесконечности. Другими словами, скорость роста f(x) асимптотически пропорциональна скорости роста g(n).
- f(x)=O(g(n)). Здесь темпы роста не быстрее, чем g (n). O большое является наиболее полезной, поскольку представляет наихудший случай.
Короче говоря, если алгоритм имеет сложность __ тогда его эффективность __

График роста O — большое
