После нескольких часов чтения обзоров, Боб с нетерпением нажал на кнопку перехода к оформлению заказа на галлон цельного молока, и…
Воу, что только что произошло?

За 220 миллисекунд произошло множество интересных вещей, из-за которых Firefox сменил цвет адресной строки и отобразил замочек в правом нижнем углу. С помощью моего любимого инструмента Wireshark и немного модифицированной отладочной сборки Firefox мы попробуем разобраться, что же именно произошло.
По RFC 2818 Firefox знает, что «https» означает, что нужно использовать 443 порт для подключения к Amazon.com:
TLS заворачивает весь траффик в «записи» различных типов. Мы видим, что первый байт пакета в HEX равен 0x16 = 22, что означает, что «запись» является «рукопожатием»:

Следующие два байта — 0x0301, означающие версию 3.1, что говорит о том, что TLS 1.0 на самом деле SSL 3.1.
Запись с рукопожатием разбита на несколько сообщений. Первый — «приветствие клиента» (0x01). Здесь есть несколько важных моментов:
Amazon.com отвечает довольно крупной записью с рукопожатием, размером в два пакета (2,551 байт). В ней указана та же последовательность байт 0x0301, что означает согласие Amazon использовать TLS 1.0. В записи есть три подсообщения с интересными данными:
Сертификаты нужны для того, чтобы браузер мог удостовериться, что общается именно с Amazon.com. Он смотрит на даты начала и окончания срока действия сертификата, а также проверяет, авторизован ли публичный ключ для обмена секретными ключами.
Почему мы должны доверять сертификатам?
К нему прикреплена «подпись», длинное число в формате big-endian:
Кто угодно мог прислать эти байты. Почему мы должны доверять этой подписи? Для ответа совершим небольшое путешествие в мир математики:
Некоторые люди задаются вопросом, имеет ли математика какую либо связь с программированием? Сертификаты — очень наглядный случай применения математики. Сертификат Amazon говорит нам, что нужно использовать RSA для проверки подписи. RSA был создан в 1970 профессорами MIT Ron Rivest, Adu Shamir и Len Adleman, нашедшими красивый способ соединить идеи, появившиеся за 2000 лет развития математки и создать простой алгоритм:
Вы выбираете два простых числа, p и q. Умножаете их и получаете n. Далее, вы выбираете простую публичную экспоненту e, которая будет шифрующей экспонентой, и специально подобранную обратную e, d, которая будет дешифрующей. Затем вы делаете n и e публичными и храните d в секрете. Про p и q можно забыть, или же хранить вместе с d.
Теперь, если у вас есть сообщение, вам нужно просто представить его байты как число M. Если нужно зашифровать сообщение, высчитываем:
C ≡ Me (mod n)
Это означает, что нужно умножить M на себя e раз. mod n означает, что мы берём только остаток от деления на n. Например, 11 AM + 3 часа = 2PM (mod 12 часов). Получатель знает d и может произвести обратную операцию для расшифровки:
Cd ≡ (Me)d ≡ Me*d ≡ M1 ≡ M (mod n)
Также интересно, что человек с d может подписать документ возведя сообщение M в степень d:
Md ≡ S (mod n)
Это возможно благодаря тому, что подписывающая сторона делает публичными S, M, e и n. Кто угодно может проверить подпись S с помощью простых вычислений:
Se ≡ (Md)e ≡ Md*e ≡ Me*d ≡ M1 ≡ M (mod n)
Криптография с публичным ключом часто называется асимметричной, потому что ключ шифрования (в нашем случае e) не равен ключу дешифровки (d). Магия RSA работает из-за того, что вы можете рассчитать C ≡ Me (mod n) довольно быстро, но почти невозможно Cd ≡ M (mod n) не зная d. Как мы уже убедились ранее, d полуается из факторизации n обратно к p и q, что довольно-таки сложно.
Работая с RSA в реальной жизни важно помнить, что все числа должны быть __очень__ большими. Насколько? Сертификат Amazon подписан «VeriSign Class 3 Secure Server CA». Это значит, что n должно быть 2048 бит длинной, что в десятичном виде:
1890572922 9464742433 9498401781 6528521078 8629616064 3051642608 4317020197 7241822595 6075980039 8371048211 4887504542 4200635317 0422636532 2091550579 0341204005 1169453804 7325464426 0479594122 4167270607 6731441028 3698615569 9947933786 3789783838 5829991518 1037601365 0218058341 7944190228 0926880299 3425241541 4300090021 1055372661 2125414429 9349272172 5333752665 6605550620 5558450610 3253786958 8361121949 2417723618 5199653627 5260212221 0847786057 9342235500 9443918198 9038906234 1550747726 8041766919 1500918876 1961879460 3091993360 6376719337 6644159792 1249204891 7079005527 7689341573 9395596650 5484628101 0469658502 1566385762 0175231997 6268718746 7514321
(Удачи с подбором p и q. Если получится — можно сгенирировать поддельный VeriSign сертификат.)
Если мы возведём подпись S в степень публичного e VeriSign, а затем возьмём остаток от деления на модуль n, то получим расшифрованную подпись в hex:
0001FFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFF00302130 0906052B0E03021A 05000414C19F8786 871775C60EFE0542 E4C2167C830539DB
По стандарту PKCS #1 v1.5, первый байт 00 для того, чтобы блок шифрования, сконвертированный в integer, был меньше, чем модуль(так и не понял, что за модуль — прим. перев.). Второй байт 01 указывает на то, что это операция с приватным ключом. Затем куча FF байт для того, чтобы забить пустое место. Завершается оно байтом 00, затем идёт последовательность «30 21 30 09 06 05 2B 0E 03 02 1A 05 00 04 14», что означает применение SHA-1 функции. Последние 20 байт — результат SHA-1 от байт в signedCertificate.
Так как расшифрованное значение правильно отформатировано и последние байты соответствуют тем, что мы можем посчитать сами, мы можем предположить, что кто-то знающий приватный ключ «VeriSign Class 3 Secure Server CA» подписал это.
Можно повторить процесс и удостовериться в том, что сертифика «VeriSign Class 3 Secure Server CA» был подписан VeriSign «Class 3 Public Primary Certification Authority».
Но почему надо ему доверять? В этой цепочке доверия нет больше звеньев.

Корневой «VeriSign Class 3 Public Primary Certification Authority» был подписан сам собой. Этот сертификат встроен в продукты Mozilla как безоговорочно доверенный сертификат.
Мы проверили Amazon.com и знаем его публичную шифрующую экспоненту e и модуль n. Кто угодно прослушивающий нас может сделать то же самое. Теперь нам надо сгенерировать случайный ключ, который атакующий не узнает. Это не так просто как может показаться, из-за уязвимости псевдогенератора случайных чисел в Netscape Navigator 1.1 SSL можно было взломать за 25 секунд на машинах того времени. Если не верите, что настоящая случайность — это сложно, можете спросить мэинтейнеров OpenSSL в Debian.
На Windows, например, функция генерации псевдослучайных чисел берёт данные из 125 источников. Firefox использует её результат и добавляет несколько бит собственных псевдослучайных данных
Очень важно держать в секрете 48-байтовы «pre-master ключ», так как многие вещи выводятся именно из него. Не удивительно, что в Firefox так сложно его найти. Мне пришлось собрать отладочную версию и установить флаги SSLDEBUGFILE и SSLTRACE чтобы его увидеть
4456: SSL[131491792]: Pre-Master Secret [Len: 48]
03 01 bb 7b 08 98 a7 49 de e8 e9 b8 91 52 ec 81 ...{...I.....R…
4c c2 39 7b f6 ba 1c 0a b1 95 50 29 be 02 ad e6 L.9{......P)…
ad 6e 11 3f 20 c4 66 f0 64 22 57 7e e1 06 7a 3b .n.? .f.d«W~..z;
Он не совсем случаен, первые два байта по стандарту TLS должны быть 03 01.
Обмен ключами
Теперь нам надо передать это секретное число в Amazon.com. Так как Amazon пожелал использовать „TLS_RSA_WITH_RC4_128_MD5“, мы зашифруем его RSA. Можно использовать в качестве сообщения только 48 байт pre-master ключа, но по стандарту PKCS #1 v1.5 нужно забить пустое место случайными данными и довести размер пакета до 128 байт. Так будет сложнее расшифровать пакет атакующему.
Наконец, Firefox отправляет последнее незашифрованное сообщение, запись „Change Cipher Spec“:

Это способ Firefox сказать Amazon, что он собирается использовать переданные ранее секретные ключи для следующих сообщений.
Вычисление Master Secret
Если мы сделали всё верно, то обе стороны теперь знают 48 байт pre-master ключа. Со стороны Amazon есть лёгкое недоверие, так как pre-master содержит только данные клиента и не содержит данных сервера. Исправим это вычислив master key.
master_secret = PRF(pre_master_secret, „master secret“, ClientHello.random + ServerHello.random)
PRF — псевдорандомная функция, которая определена в спецификациях и довольно хитра. В ней используются HMAC версии MD5 и SHA-1. По половине ввода отправляется в каждую функцию, получается результат, весьма устойчивый к атакам.
В результате получаем 48 байт master secret.
4C AF 20 30 8F 4C AA C5 66 4A 02 90 F2 AC 10 00 39 DB 1D E0 1F CB E0 E0 9D D7 E6 BE 62 A4 6C 18 06 AD 79 21 DB 82 1D 53 84 DB 35 A7 1F C1 01 19
Генерируем остальные ключи
Теперь, когда у двух сторон есть master secret, по спецификации мы можем вычислить все нужные для сессии ключи используя PRF для создания „блока ключей“, из которого и возьмём нужные данные:
key_block = PRF(SecurityParameters.master_secret, „key expansion“, SecurityParameters.server_random + SecurityParameters.client_random);
Байты из „блока ключей“ нужны для:
client_write_MAC_secret[SecurityParameters.hash_size]
server_write_MAC_secret[SecurityParameters.hash_size]
client_write_key[SecurityParameters.key_material_length]
server_write_key[SecurityParameters.key_material_length]
client_write_IV[SecurityParameters.IV_size]
server_write_IV[SecurityParameters.IV_size]
Так как мы используем потоковое, а не блочное шифрование, нам не нужны векторы инициализации. Тем не менее, нам нужны два Message Authentication Code (MAC) ключа для каждой стороны, каждый по 16 байт, так как длина результата MD5 тоже 16 байт. К тому же RC4 использует 16 байтный ключ, который также понадобится обеим сторонам. В общем, нам понадобятся 2*16 + 2*16 = 64 байта из блока ключей
Запуская PRF, получаем:
client_write_MAC_secret = 80 B8 F6 09 51 74 EA DB 29 28 EF 6F 9A B8 81 B0
server_write_MAC_secret = 67 7C 96 7B 70 C5 BC 62 9D 1D 1F 4A A6 79 81 61
client_write_key = 32 13 2C DD 1B 39 36 40 84 4A DE E5 6C 52 46 72
server_write_key = 58 36 C4 0D 8C 7C 74 DA 6D B7 34 0A 91 B6 8F A7
Приготовтесь быть зашифрованными!
Последнее сообщение рукопожатия, отправляемое клиентом — „Финальное сообщение“. Это хитрое сообщение, которое доказывает, что никто не подделал рукопожатие и доказывает, что мы знаем ключ. Клиент берёт все байты из сообщений рукопожатия и складывает в буфер. Потом высчитываются 12 байт подтвеждения с использованием генератора псевдослучайных чисел, master key, строки „client finished“, и MD5 и SHA-1 от буфера.
verify_data = PRF(master_secret, „client finished“, MD5(handshake_messages) + SHA-1(handshake_messages))
Берём результат и добавляем в заголовок байт 0x14, указывающий на завершение, и байты длины 00 00 0с, чтобы показать, что мы отправляем 12 байт. Затем, как в будущем и для всех зашифрованных сообщений, нужно удостовериться, что расшифрованное содержимое никто не подделал. Используем MD5, а точнее его HMAC версию.
HMAC_MD5(Key, m) = MD5((Key ⊕ opad) ++ MD5((Key ⊕ ipad) ++ m)
(⊕ означает XOR, ++ означает конкатенацию, „opad“ это байты „5c 5c… 5c“, и „ipad“ это байты „36 36… 36“).
В общем, мы высчитываем:
HMAC_MD5(client_write_MAC_secret, seq_num + TLSCompressed.type + TLSCompressed.version + TLSCompressed.length + TLSCompressed.fragment));
Как вы могли заметить, мы подмешиваем номер запроса, который защищает от специфической атаки с повторением пакета.
Осталось только зашифровать.
Выбранный набор алгоритмов шифрования говорит нам использовать RC4. Он настолько прост, что вы можете выучить его за пару минут.
RC4 начинается с создания 256 байтного массива S и заполнением его значениями от 0 до 255. Затем нужно пройти по массиву „вмешивая“ байты ключа. Это делается для создания автомата состояний, используемого для генерирования случайных байт. Затем мы перемешиваем массив S.
Графически это можно представить так:

Чтобы зашифровать байт, мы XORим псевдослучайный байт с байтом, который надо зашифровать.
Итак, всё довольно просто, и быстро работает. Мне кажется, из-за этого Amazon выбрал этот алгоритм.
Вспомним, что у нас есть „client_write_key“ и „server_write_key“. Это значит, что нам нужно два экземпляра RC4: один для расшифровки ответов, другой — для шифрования запросов.
Первые несколько случайных байт из „client_write“ это „7E 20 7A 4D FE FB 78 A7 33 ...“. Если поXORить эти байты с незашифрованным заголовком и проверить байты сообщения „14 00 00 0C 98 F0 AE CB C4 ...“, то получим то, что можно видеть на скриншоте Wireshark ниже:
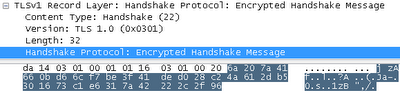
Сервер делает почти то же самое. Он посылает „Change Cipher Spec“, а затем „финальное“ сообщение, которое включает все сообщения рукопожатия и незашифрованное „финальное“ сообщение. Это доказывает клиенту, что сервер смог расшифровать его сообщения.
Сейчас, через 220 миллисекунд (три часа спустя — прим. перев.), мы наконец готовы использовать прикладной уровень. Теперь можно обмениваться обычным HTTP траффиком, который будет зашифрован TLS с применением RC4 и проверен на случай подмены.
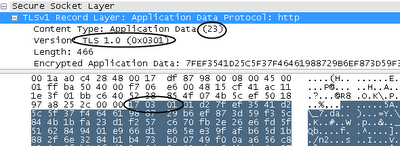
Сейчас рукопожатие завершено. Содержимое записи TLS теперь 0x17. Шифрованый траффик начинается с 17 03 01, что указывает на тип записи и версию TLS.
Шифрование пакета:
GET /gp/cart/view.html/ref=pd_luc_mri HTTP/1.1
Host: www.amazon.com
User-Agent: Mozilla/5.0 (Windows; U; Windows NT 6.0; en-US; rv:1.9.0.10) Gecko/2009060911 Minefield/3.0.10 (.NET CLR 3.5.30729)
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
Accept-Language: en-us,en;q=0.5
Accept-Encoding: gzip,deflate
Accept-Charset: ISO-8859-1,utf-8;q=0.7,*;q=0.7
Keep-Alive: 300
Connection: keep-alive
…
даст примерно следующий результат:

Сервер делает то же самое. Расшифровка даёт нам следующее:

HTTP/1.1 200 OK
Date: Wed, 10 Jun 2009 01:09:30 GMT
Server: Server
…
Conection: close
Transfer-Encoding: chunked
Соединение остаётся открытым до тех пор, пока любая сторона не отправит сообщение, предупреждающее о завершении, а затем закроет соединение. Если мы переподключимся незадолго после закрытия предыдущего соединения, мы можем использовать старые ключи чтобы не проводить процедуру рукопожатия заново.
Важно понимать, что на прикладном уровне может быть абсолютно что угодно. Есть множество других основанных на TCP/IP протоколов, которые могут работать поверх TLS. Например, FTPS. Всегда лучше использовать TLS вместо изобретения своего велосипеда.
TLS RFC покрывает множество деталей, которые мы не обсудили. Мы рассмотрели лишь 220 миллисекундный танец между Firefox и Amazon. Узнали, что если кто-то разложит число n Amazon в p и q, то сможет расшифровать весь траффик Amazon, пока тот не сменит сертификат.
Всего за 220 миллисекунд две точки в Интернете соединились, предоставили друг другу достаточно данных для доверия, настроили алгоритмы шифрования и начали обмениваться зашифрованным траффиком.
И всё для того, чтобы Боб мог купить молочка.
Воу, что только что произошло?
За 220 миллисекунд произошло множество интересных вещей, из-за которых Firefox сменил цвет адресной строки и отобразил замочек в правом нижнем углу. С помощью моего любимого инструмента Wireshark и немного модифицированной отладочной сборки Firefox мы попробуем разобраться, что же именно произошло.
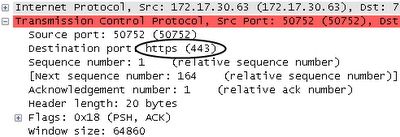
По RFC 2818 Firefox знает, что «https» означает, что нужно использовать 443 порт для подключения к Amazon.com:

Приветствие клиента
TLS заворачивает весь траффик в «записи» различных типов. Мы видим, что первый байт пакета в HEX равен 0x16 = 22, что означает, что «запись» является «рукопожатием»:

Следующие два байта — 0x0301, означающие версию 3.1, что говорит о том, что TLS 1.0 на самом деле SSL 3.1.
Запись с рукопожатием разбита на несколько сообщений. Первый — «приветствие клиента» (0x01). Здесь есть несколько важных моментов:
- Случайность:

Эти четыре байта — текущее Unix time, количество секунд с 1 Января, 1970. В нашем случае это 0x4a2f07ca. За ними идут 28 случайных байт, которые понадобятся позже. - ID сессии:

В нашем случае это поле пусто. Если бы мы подключались к Amazon.com несколькими секундами ранее, то могли бы продолжить сессию и не проводить полное рукопожатие. - Cipher Suites:

Список всех поддерживаемых браузером алгоритмов шифрования. По умолчанию используется очень сильный «TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA», за которым идут ещё 33 варианта. Не волнуйтесь, если ничего не понимаете. Далее мы узнаем, что Amazon не примет наш вариант по умолчанию. - Расширение server_name:

Способ сказать amazon.com, что браузеру нужна страница по адресу www.amazon.com. Это довольно удобно, потому что TLS рукопожатие начинается задолго до HTTP траффика. В HTTP есть заголовок «Host», позволяющий хостить сотни сайтов на одном IP. SSL традиционно требовал разные IP для разных сайтов, но это расширение позволяет серверу отвечать сертификатом конкретного сайта.
Приветствие сервера
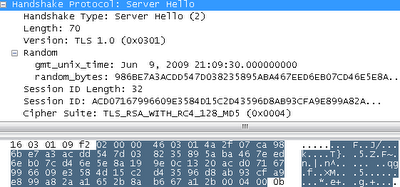
Amazon.com отвечает довольно крупной записью с рукопожатием, размером в два пакета (2,551 байт). В ней указана та же последовательность байт 0x0301, что означает согласие Amazon использовать TLS 1.0. В записи есть три подсообщения с интересными данными:
- Сообщение «Приветствие сервера»:

- Четыре байта Unix time и 28 случайных байт.
- ID сессии в 32 байтах для ускорения следующих запросов.
- Из 34 алгоритмов, предложенных нами, Amazon выбрал «TLS_RSA_WITH_RC4_128_MD5» (0x0004). Это означает, что будет использоваться алгоритм RSA для проверки подписей сертификата и обмена ключами, алгоритм RC4 для шифрования данных, хэш функция MD5 для проверки содержимого. Мы обсудим всё это более подробно позже. Мне кажется, у Amazon есть свои причины для выбора именно этих алгоритмов, например, снижение нагрузки на CPU. Менее вероятный вариант — благодарность Ron Rivest, создателю всех трёх вышеуказанных алгоритмов.
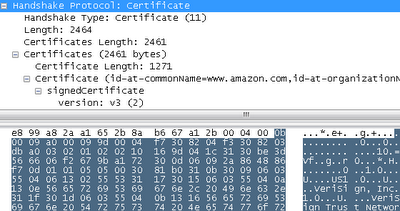
- Сообщение с сертификатом:

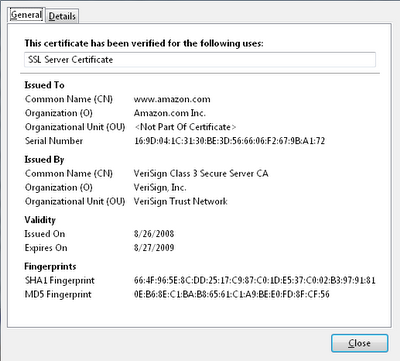
- Огромное сообщение в 2.464 байта и его сертификат, который клиент может использовать для валидации сертификата Amazon. Всё это также можно посмотреть в браузере.

- Огромное сообщение в 2.464 байта и его сертификат, который клиент может использовать для валидации сертификата Amazon. Всё это также можно посмотреть в браузере.
- Сообщение «Приветствие сервера выполнено»

Пустое сообщение, сообщающее об успешном завершении «приветствия» и говорящее о том, что сервер не будет запрашивать сертификатов клиента.
Проверка сертификата
Сертификаты нужны для того, чтобы браузер мог удостовериться, что общается именно с Amazon.com. Он смотрит на даты начала и окончания срока действия сертификата, а также проверяет, авторизован ли публичный ключ для обмена секретными ключами.
Почему мы должны доверять сертификатам?
К нему прикреплена «подпись», длинное число в формате big-endian:

Кто угодно мог прислать эти байты. Почему мы должны доверять этой подписи? Для ответа совершим небольшое путешествие в мир математики:
Небольшое введение в RSA
Некоторые люди задаются вопросом, имеет ли математика какую либо связь с программированием? Сертификаты — очень наглядный случай применения математики. Сертификат Amazon говорит нам, что нужно использовать RSA для проверки подписи. RSA был создан в 1970 профессорами MIT Ron Rivest, Adu Shamir и Len Adleman, нашедшими красивый способ соединить идеи, появившиеся за 2000 лет развития математки и создать простой алгоритм:
Вы выбираете два простых числа, p и q. Умножаете их и получаете n. Далее, вы выбираете простую публичную экспоненту e, которая будет шифрующей экспонентой, и специально подобранную обратную e, d, которая будет дешифрующей. Затем вы делаете n и e публичными и храните d в секрете. Про p и q можно забыть, или же хранить вместе с d.
Теперь, если у вас есть сообщение, вам нужно просто представить его байты как число M. Если нужно зашифровать сообщение, высчитываем:
C ≡ Me (mod n)
Это означает, что нужно умножить M на себя e раз. mod n означает, что мы берём только остаток от деления на n. Например, 11 AM + 3 часа = 2PM (mod 12 часов). Получатель знает d и может произвести обратную операцию для расшифровки:
Cd ≡ (Me)d ≡ Me*d ≡ M1 ≡ M (mod n)
Также интересно, что человек с d может подписать документ возведя сообщение M в степень d:
Md ≡ S (mod n)
Это возможно благодаря тому, что подписывающая сторона делает публичными S, M, e и n. Кто угодно может проверить подпись S с помощью простых вычислений:
Se ≡ (Md)e ≡ Md*e ≡ Me*d ≡ M1 ≡ M (mod n)
Криптография с публичным ключом часто называется асимметричной, потому что ключ шифрования (в нашем случае e) не равен ключу дешифровки (d). Магия RSA работает из-за того, что вы можете рассчитать C ≡ Me (mod n) довольно быстро, но почти невозможно Cd ≡ M (mod n) не зная d. Как мы уже убедились ранее, d полуается из факторизации n обратно к p и q, что довольно-таки сложно.
Проверка подписей
Работая с RSA в реальной жизни важно помнить, что все числа должны быть __очень__ большими. Насколько? Сертификат Amazon подписан «VeriSign Class 3 Secure Server CA». Это значит, что n должно быть 2048 бит длинной, что в десятичном виде:
1890572922 9464742433 9498401781 6528521078 8629616064 3051642608 4317020197 7241822595 6075980039 8371048211 4887504542 4200635317 0422636532 2091550579 0341204005 1169453804 7325464426 0479594122 4167270607 6731441028 3698615569 9947933786 3789783838 5829991518 1037601365 0218058341 7944190228 0926880299 3425241541 4300090021 1055372661 2125414429 9349272172 5333752665 6605550620 5558450610 3253786958 8361121949 2417723618 5199653627 5260212221 0847786057 9342235500 9443918198 9038906234 1550747726 8041766919 1500918876 1961879460 3091993360 6376719337 6644159792 1249204891 7079005527 7689341573 9395596650 5484628101 0469658502 1566385762 0175231997 6268718746 7514321
(Удачи с подбором p и q. Если получится — можно сгенирировать поддельный VeriSign сертификат.)
Если мы возведём подпись S в степень публичного e VeriSign, а затем возьмём остаток от деления на модуль n, то получим расшифрованную подпись в hex:
0001FFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFF00302130 0906052B0E03021A 05000414C19F8786 871775C60EFE0542 E4C2167C830539DB
По стандарту PKCS #1 v1.5, первый байт 00 для того, чтобы блок шифрования, сконвертированный в integer, был меньше, чем модуль(так и не понял, что за модуль — прим. перев.). Второй байт 01 указывает на то, что это операция с приватным ключом. Затем куча FF байт для того, чтобы забить пустое место. Завершается оно байтом 00, затем идёт последовательность «30 21 30 09 06 05 2B 0E 03 02 1A 05 00 04 14», что означает применение SHA-1 функции. Последние 20 байт — результат SHA-1 от байт в signedCertificate.
Так как расшифрованное значение правильно отформатировано и последние байты соответствуют тем, что мы можем посчитать сами, мы можем предположить, что кто-то знающий приватный ключ «VeriSign Class 3 Secure Server CA» подписал это.
Можно повторить процесс и удостовериться в том, что сертифика «VeriSign Class 3 Secure Server CA» был подписан VeriSign «Class 3 Public Primary Certification Authority».
Но почему надо ему доверять? В этой цепочке доверия нет больше звеньев.
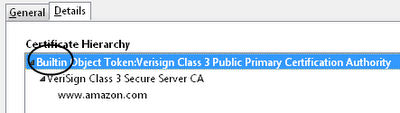
Корневой «VeriSign Class 3 Public Primary Certification Authority» был подписан сам собой. Этот сертификат встроен в продукты Mozilla как безоговорочно доверенный сертификат.
Pre-master Ключ
Мы проверили Amazon.com и знаем его публичную шифрующую экспоненту e и модуль n. Кто угодно прослушивающий нас может сделать то же самое. Теперь нам надо сгенерировать случайный ключ, который атакующий не узнает. Это не так просто как может показаться, из-за уязвимости псевдогенератора случайных чисел в Netscape Navigator 1.1 SSL можно было взломать за 25 секунд на машинах того времени. Если не верите, что настоящая случайность — это сложно, можете спросить мэинтейнеров OpenSSL в Debian.
На Windows, например, функция генерации псевдослучайных чисел берёт данные из 125 источников. Firefox использует её результат и добавляет несколько бит собственных псевдослучайных данных
Очень важно держать в секрете 48-байтовы «pre-master ключ», так как многие вещи выводятся именно из него. Не удивительно, что в Firefox так сложно его найти. Мне пришлось собрать отладочную версию и установить флаги SSLDEBUGFILE и SSLTRACE чтобы его увидеть
4456: SSL[131491792]: Pre-Master Secret [Len: 48]
03 01 bb 7b 08 98 a7 49 de e8 e9 b8 91 52 ec 81 ...{...I.....R…
4c c2 39 7b f6 ba 1c 0a b1 95 50 29 be 02 ad e6 L.9{......P)…
ad 6e 11 3f 20 c4 66 f0 64 22 57 7e e1 06 7a 3b .n.? .f.d«W~..z;
Он не совсем случаен, первые два байта по стандарту TLS должны быть 03 01.
Обмен ключами
Теперь нам надо передать это секретное число в Amazon.com. Так как Amazon пожелал использовать „TLS_RSA_WITH_RC4_128_MD5“, мы зашифруем его RSA. Можно использовать в качестве сообщения только 48 байт pre-master ключа, но по стандарту PKCS #1 v1.5 нужно забить пустое место случайными данными и довести размер пакета до 128 байт. Так будет сложнее расшифровать пакет атакующему.
Наконец, Firefox отправляет последнее незашифрованное сообщение, запись „Change Cipher Spec“:

Это способ Firefox сказать Amazon, что он собирается использовать переданные ранее секретные ключи для следующих сообщений.
Вычисление Master Secret
Если мы сделали всё верно, то обе стороны теперь знают 48 байт pre-master ключа. Со стороны Amazon есть лёгкое недоверие, так как pre-master содержит только данные клиента и не содержит данных сервера. Исправим это вычислив master key.
master_secret = PRF(pre_master_secret, „master secret“, ClientHello.random + ServerHello.random)
PRF — псевдорандомная функция, которая определена в спецификациях и довольно хитра. В ней используются HMAC версии MD5 и SHA-1. По половине ввода отправляется в каждую функцию, получается результат, весьма устойчивый к атакам.
В результате получаем 48 байт master secret.
4C AF 20 30 8F 4C AA C5 66 4A 02 90 F2 AC 10 00 39 DB 1D E0 1F CB E0 E0 9D D7 E6 BE 62 A4 6C 18 06 AD 79 21 DB 82 1D 53 84 DB 35 A7 1F C1 01 19
Генерируем остальные ключи
Теперь, когда у двух сторон есть master secret, по спецификации мы можем вычислить все нужные для сессии ключи используя PRF для создания „блока ключей“, из которого и возьмём нужные данные:
key_block = PRF(SecurityParameters.master_secret, „key expansion“, SecurityParameters.server_random + SecurityParameters.client_random);
Байты из „блока ключей“ нужны для:
client_write_MAC_secret[SecurityParameters.hash_size]
server_write_MAC_secret[SecurityParameters.hash_size]
client_write_key[SecurityParameters.key_material_length]
server_write_key[SecurityParameters.key_material_length]
client_write_IV[SecurityParameters.IV_size]
server_write_IV[SecurityParameters.IV_size]
Так как мы используем потоковое, а не блочное шифрование, нам не нужны векторы инициализации. Тем не менее, нам нужны два Message Authentication Code (MAC) ключа для каждой стороны, каждый по 16 байт, так как длина результата MD5 тоже 16 байт. К тому же RC4 использует 16 байтный ключ, который также понадобится обеим сторонам. В общем, нам понадобятся 2*16 + 2*16 = 64 байта из блока ключей
Запуская PRF, получаем:
client_write_MAC_secret = 80 B8 F6 09 51 74 EA DB 29 28 EF 6F 9A B8 81 B0
server_write_MAC_secret = 67 7C 96 7B 70 C5 BC 62 9D 1D 1F 4A A6 79 81 61
client_write_key = 32 13 2C DD 1B 39 36 40 84 4A DE E5 6C 52 46 72
server_write_key = 58 36 C4 0D 8C 7C 74 DA 6D B7 34 0A 91 B6 8F A7
Приготовтесь быть зашифрованными!
Последнее сообщение рукопожатия, отправляемое клиентом — „Финальное сообщение“. Это хитрое сообщение, которое доказывает, что никто не подделал рукопожатие и доказывает, что мы знаем ключ. Клиент берёт все байты из сообщений рукопожатия и складывает в буфер. Потом высчитываются 12 байт подтвеждения с использованием генератора псевдослучайных чисел, master key, строки „client finished“, и MD5 и SHA-1 от буфера.
verify_data = PRF(master_secret, „client finished“, MD5(handshake_messages) + SHA-1(handshake_messages))
Берём результат и добавляем в заголовок байт 0x14, указывающий на завершение, и байты длины 00 00 0с, чтобы показать, что мы отправляем 12 байт. Затем, как в будущем и для всех зашифрованных сообщений, нужно удостовериться, что расшифрованное содержимое никто не подделал. Используем MD5, а точнее его HMAC версию.
HMAC_MD5(Key, m) = MD5((Key ⊕ opad) ++ MD5((Key ⊕ ipad) ++ m)
(⊕ означает XOR, ++ означает конкатенацию, „opad“ это байты „5c 5c… 5c“, и „ipad“ это байты „36 36… 36“).
В общем, мы высчитываем:
HMAC_MD5(client_write_MAC_secret, seq_num + TLSCompressed.type + TLSCompressed.version + TLSCompressed.length + TLSCompressed.fragment));
Как вы могли заметить, мы подмешиваем номер запроса, который защищает от специфической атаки с повторением пакета.
Осталось только зашифровать.
RC4 Шифрование
Выбранный набор алгоритмов шифрования говорит нам использовать RC4. Он настолько прост, что вы можете выучить его за пару минут.
RC4 начинается с создания 256 байтного массива S и заполнением его значениями от 0 до 255. Затем нужно пройти по массиву „вмешивая“ байты ключа. Это делается для создания автомата состояний, используемого для генерирования случайных байт. Затем мы перемешиваем массив S.
Графически это можно представить так:

Чтобы зашифровать байт, мы XORим псевдослучайный байт с байтом, который надо зашифровать.
Итак, всё довольно просто, и быстро работает. Мне кажется, из-за этого Amazon выбрал этот алгоритм.
Вспомним, что у нас есть „client_write_key“ и „server_write_key“. Это значит, что нам нужно два экземпляра RC4: один для расшифровки ответов, другой — для шифрования запросов.
Первые несколько случайных байт из „client_write“ это „7E 20 7A 4D FE FB 78 A7 33 ...“. Если поXORить эти байты с незашифрованным заголовком и проверить байты сообщения „14 00 00 0C 98 F0 AE CB C4 ...“, то получим то, что можно видеть на скриншоте Wireshark ниже:
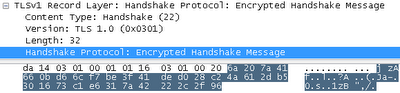
Сервер делает почти то же самое. Он посылает „Change Cipher Spec“, а затем „финальное“ сообщение, которое включает все сообщения рукопожатия и незашифрованное „финальное“ сообщение. Это доказывает клиенту, что сервер смог расшифровать его сообщения.
Добро пожаловать на прикладной уровень!
Сейчас, через 220 миллисекунд (три часа спустя — прим. перев.), мы наконец готовы использовать прикладной уровень. Теперь можно обмениваться обычным HTTP траффиком, который будет зашифрован TLS с применением RC4 и проверен на случай подмены.
Сейчас рукопожатие завершено. Содержимое записи TLS теперь 0x17. Шифрованый траффик начинается с 17 03 01, что указывает на тип записи и версию TLS.
Шифрование пакета:
GET /gp/cart/view.html/ref=pd_luc_mri HTTP/1.1
Host: www.amazon.com
User-Agent: Mozilla/5.0 (Windows; U; Windows NT 6.0; en-US; rv:1.9.0.10) Gecko/2009060911 Minefield/3.0.10 (.NET CLR 3.5.30729)
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
Accept-Language: en-us,en;q=0.5
Accept-Encoding: gzip,deflate
Accept-Charset: ISO-8859-1,utf-8;q=0.7,*;q=0.7
Keep-Alive: 300
Connection: keep-alive
…
даст примерно следующий результат:

Сервер делает то же самое. Расшифровка даёт нам следующее:
HTTP/1.1 200 OK
Date: Wed, 10 Jun 2009 01:09:30 GMT
Server: Server
…
Conection: close
Transfer-Encoding: chunked
Соединение остаётся открытым до тех пор, пока любая сторона не отправит сообщение, предупреждающее о завершении, а затем закроет соединение. Если мы переподключимся незадолго после закрытия предыдущего соединения, мы можем использовать старые ключи чтобы не проводить процедуру рукопожатия заново.
Важно понимать, что на прикладном уровне может быть абсолютно что угодно. Есть множество других основанных на TCP/IP протоколов, которые могут работать поверх TLS. Например, FTPS. Всегда лучше использовать TLS вместо изобретения своего велосипеда.
На этом всё!
TLS RFC покрывает множество деталей, которые мы не обсудили. Мы рассмотрели лишь 220 миллисекундный танец между Firefox и Amazon. Узнали, что если кто-то разложит число n Amazon в p и q, то сможет расшифровать весь траффик Amazon, пока тот не сменит сертификат.
Всего за 220 миллисекунд две точки в Интернете соединились, предоставили друг другу достаточно данных для доверия, настроили алгоритмы шифрования и начали обмениваться зашифрованным траффиком.
И всё для того, чтобы Боб мог купить молочка.