
Всем привет. В этой статье я хотел бы рассказать немного об основных приемах и идеях современной цифровой беспроводной связи — на примере стандарта IEEE 802.11. В наше время очень часто люди живут на довольно высоких уровнях абстракции, плохо представляя как именно работают окружающие нас вещи. Ну что ж — попытаюсь принести в массы свет просвещения. В статье будут использоваться вещи и терминология, объясненные в этой статье. Так что людям, далеким от радиотехники рекомендуется сначала прочитать её.
DANGER: в статье присутствует матан — особо впечатлительным не нажимать на эту кнопку:
Цифровые сигналы и спектры
Аналоговые сигналы
До развития компьютеров — посредством радиоволн передавались обычно аналоговые сигналы — то есть сигналы, множество значений которых непрерывно.
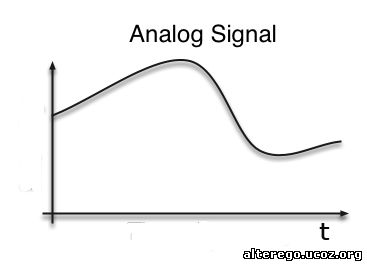
Например — звук — зависимость давления от времени. Полученный с приемника сигнал (напряжение) поступает на усилитель звуковой частоты и заставляет колебаться динамик.
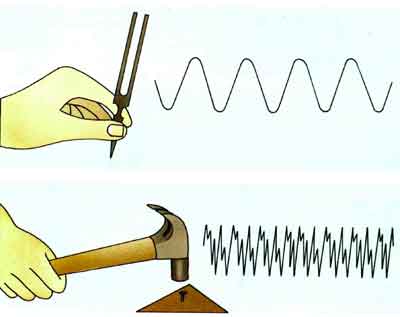
Или видеосигнал для кинескопа. Уровень сигнала определяет значение мощности, бегающего по экрану лучика, который в нужные моменты времени засвечивает люминофор, формируя изображение на экране
Основной минус такого способа передачи информации — низкая помехоустойчивость — передающая среда всегда вносит в наш сигнал какую то случайную составляющую — изменение формы видеосигнала меняет цвета отдельных пикселей(все мы помним шумы радиоприемника и рябь на экране телевизора).
Цифровые сигналы
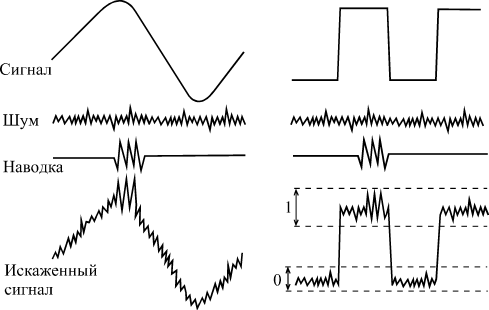
Цифровые сигналы — то есть сигналы, имеющие дискретное множество значений — по этому параметру значительно лучше аналоговых, так как нас интересует не непосредственно значение сигнала, а диапазон в котором находится это значение и помеха нам не страшна(например в диапазоне напряжений 0В — 1.6В мы считаем, что это лог 0, а в диапазоне 3.3В — 5В лог 1). Расплата за это — увеличение требуемой скорости передачи и обработки информации.
Первое, что люди научились делать — естественно передавать такие сигналы по проводам, просто переключая состояние линии данных и синхронизации из единицы в ноль.
На этом небольшой ликбез закончен — далее речь пойдет о том — а как же передается цифровой сигнал при помощи радиоволн. Как работает WiFi.
Спектр единичного импульса
В радиосвязи нас часто интересует спектр сигнала — цифровой сигнал — последовательность прямоугольных импульсов — для начала рассмотрим спектр одного прямоугольного импульса.
Вспомним — что такое спектр(коэффициент перед интегралом опущен):
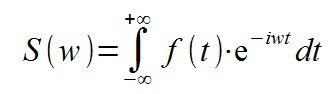
Спектр прямоугольного импульса длительностью T и амплитудой A:
Вывод
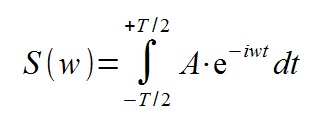
Выносим константу за интеграл и делаем замену дифференциала
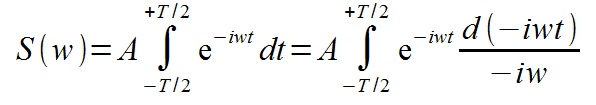
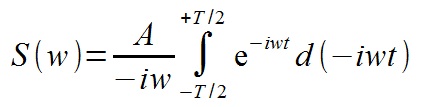
Считаем определенный интеграл

Далее делаем замену на синус по Формуле Эйлера


Выносим константу за интеграл и делаем замену дифференциала
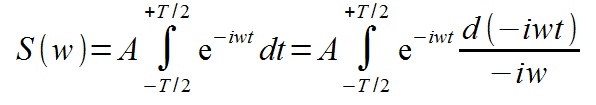
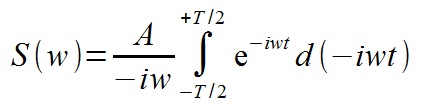
Считаем определенный интеграл
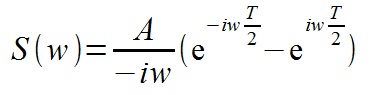
Далее делаем замену на синус по Формуле Эйлера
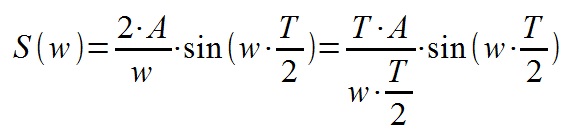
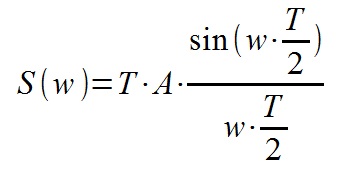
Таак — а как же быть с отрицательной амплитудой? Вспомним что в действительных числах спектр раскладывается на сумму синусов и косинусов с нулевыми фазами —

в такой форме на самом деле удобней представлять в компьютере, но для анализа такая форма совершенно неудобна — при изменениях сигнала во временнОй области — спектры будут меняться совершенно непонятным для человека образом, поэтому два спектра синусных компонент и косинусных компонент преобразуют в полярные координаты, сворачивая пары синусов и косинусов с нулевой фазой в синус с ненулевой фазой, получая амплитудный спектр и фазовый, а теперь вспомним, что домножение сигнала на -1 — эквивалентно скачку фазы на 180 градусов, поэтому отрицательная часть отразится относительно горизонтальной оси, а в точках перегиба — фаза будет испытывать скачок на 180 градусов.
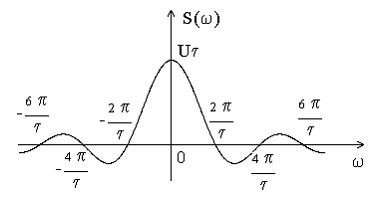
Также видим, что спектр одиночного импульса представляет собой sinc функцию, довольно часто встречающуюся в цифровой обработке сигналов и радиотехнике.
Почти вся энергия импульса содержится в центральном пике спектра — его ширина обратно пропорциональна длительности импульса. А высота — прямо пропорциональна — то есть — чем длиннее импульс — тем уже и выше его спектр, а чем короче — тем ниже и шире.
Спектр последовательности импульсов с хорошей степенью точности можно считать совокупностью гармоник в спектральной полосе, ширина которой обратно пропорциональна длительности импульса T.
Итак — вывод — уменьшая длину импульсов нашего цифрового сигнала мы можем размазывать сигнал по широкой полосе спектра — при этом пропорционально уменьшается его высота — при увеличении полосы в N раз — во столько же уменьшится высота спектра вплоть до уровня шумов. Широкополосная передача имеет довольно много плюсов — один из них — устойчивость к узкополосным помехам — так как информация размазана по спектру — узкополосная помеха портит только малую часть этой информации.
Если тупо уменьшить длину импульсов нашего информационного сигнала — спектр, конечно, уширится, но ведь приемник не знает какую информацию мы ему передаем и не сможет выделить её из шумов. Поэтому необходим способ — преобразовать узкополосный сигнал в широкополосный шумоподобный — для передачи по радиоканалу, а после приема преобразовать обратно в узкополосный — нужно добавлять в сигнал избыточную информацию, то есть информацию, известную и приемнику и передатчику, при помощи которой приемник может отличить сигнал от шумов. Закодируем каждый бит информации известной и приемнику и передатчику последовательностью.
Автокорреляционная функция. Коды Баркера
Наша задача — найти в длинной последовательности входных данных заранее известную короткую последовательность.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом.
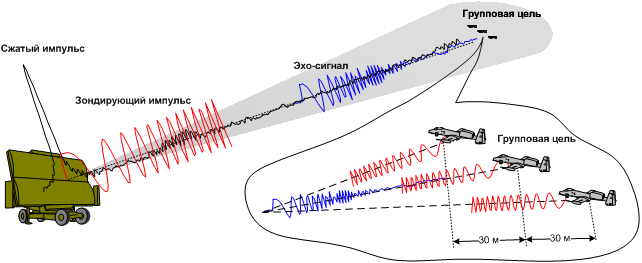
Особое значение данный параметр имеет в локации — вот сгенерировали мы какой то сигнал и засекли время — скорость распространения сигнала нам известна, значит зная время, которое потребовалось сигналу, чтобы сбегать до препятствия и обратно — мы можем вычислить расстояние для препятствия. Но вот незадача — идеальных условий в жизни не бывает — как правило вокруг очень много шумов и вместе с отраженным сигналом на вход приемника поступает всякий мусор. А мы во-первых не должны спутать наш сигнал ни с чем другим, во вторых — достаточно точно определить момент времени, когда он вернулся назад.
Математически — автокорреляция определяется так:
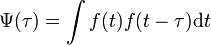
То есть мы накладываем функцию на саму себя, но со сдвигом — перемножаем и вычисляем интеграл, отмечаем точку, затем опять сдвигаем, опять вычисляем интеграл и так для всех возможных сдвигов. Если мы прикладываем функцию не к самой себе, а к какой то другой, то это называется просто корреляция.
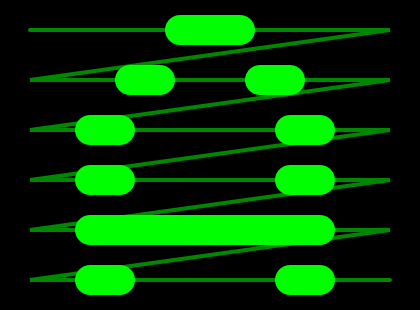
На приведенной ниже картинке демонстрируются операции свертки, корреляции и автокорреляции.
Отличие свертки и корреляции — в направлении — свертка функций f(x) и g(x) — это та же корреляция, только функций f(x) и g(-x), автокорреляция — корреляция функции с самой собой
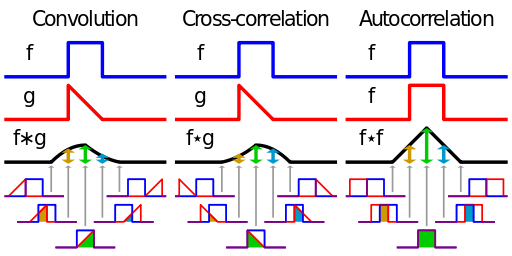
То есть в момент времени, когда входной сигнал наиболее похож на нужную нам функцию — корреляционная функция будет иметь пик. Ширина этого пика, если не брать во внимание шум — будет равна удвоенной длине зондирующего импульса и будет симметричной относительно центрального пика — даже если исследуемый сигнал не является симметричным. К слову — пиков может быть несколько — центральный пик и так называемые боковые лепестки — зависит от функции. Корреляционный метод является самым оптимальным методом определения сигнала известной формы на фоне белого шума — другими словами метод имеет наилучшее отношение сигнал/шум. Зондирующий импульс должен удовлетворять следующим требованиям — иметь как можно более узкий центральный пик и при этом иметь минимальный уровень боковых лепестков, то есть функция похожа сама на себя только в очень коротком интервале времени — чуть сдвинуть и она становится совершенно непохожа. В локации этим требованиям удовлетворяет ЛЧМ сигнал.
Имеющий минимальный уровень боковых лепестков, автокорреляционная функция ЛЧМ сигнала имеет следующий вид:
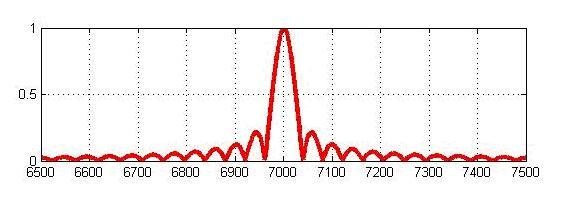
Аналогом ЛЧМ сигнала в дискретных системах является последовательность Баркера
Например — известная последовательность длинной 11 бит: 11100010010.
Найдем автокорреляционную функцию этой последовательности, циклически сдвигая её и считая сумму попарных произведений, при этом заменив 0 на -1
11100010010
11100010010
11
11100010010
01110001001
-1
11100010010
10111000100
-1
11100010010
01011100010
-1
11100010010
00101110001
-1
11100010010
10010111000
-1
…
И так далее — в общем автокорреляционная функция имеет значение 11 только при полном совпадении, во всех остальных случаях — -1.
То же самое справедливо и для инверсии последовательности, то есть для 00011101101. Плюс ко всему — прямая и инверсная последовательности слабо коррелируют между собой — мы их не спутаем.
Получается, что мы можем каждый бит информации кодировать 11 битами последовательности Баркера — прямой для единиц и инверсной для нулей. Элементы последовательности Баркера называют чипами.На практике кодирование происходит примерно так:

Приемник просто может считать корреляцию последовательностей Баркера(прямой и инверсной) и входного сигнала и по пикам корреляционной функции определять — где во входном сигнале закодированы нули, а где — единицы
Модуляция
В общем — как сделать из узкополосного информационного сигнала — широкополосный шумоподобный, а потом его восстановить — разобрались. Теперь поговорим немного о способах передачи данных через среду — средой может быть вакуум, воздух, оптоволокно, провод и т.д. Для того чтобы передавать сигнал при помощи радиоволн нам нужна несущая частота, промодулировав её — мы насаживаем нашу информацию на несущую. Есть 3 основных типа модуляции — амплитудная, частотная и фазовая.
Можно наш готовый к передаче сигнал направить на переключатель и просто включать-выключать передачу несущей — тем самым промодулировав амплитуду
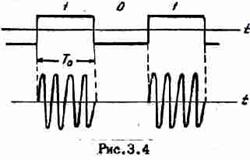
Достоинства и недостатки амплитудной модуляции рассматривались в этой статье, так что подробно здесь останавливаться на ней не будем — в настоящее время амплитудная модуляция почти не применяется.
Следующий тип модуляции — частотная, когда сигнал данных управляет частотой несущей — либо напрямую (ГУН), либо переключаясь между двумя разными генераторами(при этом происходит скачок фазы)
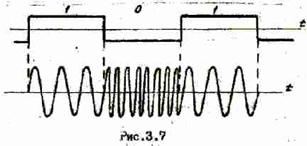
Тут тоже есть что сказать, но как нибудь в другой раз — иначе статья получится слишком уж большой.
Фазовая модуляция
Несложно догадаться — что тут мы кодируем информацию в фазе сигнала — например нуль соответствует нулевому сдвигу по фазе, а единица — сдвигу на 180 градусов — такой способ кодировки легко реализовать технически — например умножая сигнал на 1 — имеем нулевой фазовый сдвиг, а умножая на -1 — сдвиг на 180 градусов. Такая модуляция называется Binary Phase Shift Key или BPSK
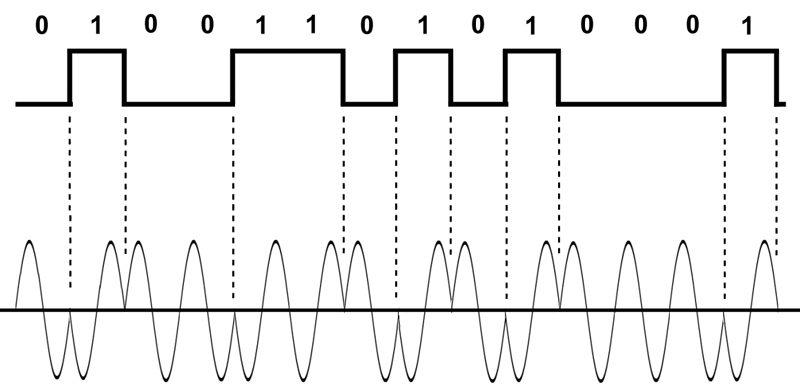
А что если мы хотим иметь больше фазовых сдвигов? Для начала объясню логику инженеров, которые придумали следующие танцы с бубном — у вас всего 2 управляющих сигнала — 1 и -1 и при помощи них нужно наиболее простым способом закодировать произвольное число фазовых сдвигов — можно конечно поставить какой нибудь супер ЦАП и управлять генерируемой частотой напрямую, но математика предлагает нам кое что получше. А именно вот эту формулу:
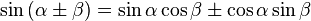
К слову — на ее основе мы произвели переход от спектров синусоид и косинусоид с нулевыми фазами к спектру синусоид с ненулевыми фазами и фазовому спектру — теперь мы просто делаем обратное преобразование.
На этом основана Квадратурная Модуляция
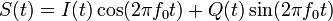
— вместе с несущей мы генерируем еще один сигнал, который сдвинут относительно несущей на 90 градусов, то есть находится с ней в квадратуре. Теперь — управляя амплитудой каждого сигнала(In phase и Quadrature) — умножая на 1 или -1, а затем суммируя — мы можем получить уже 4 возможных фазовых сдвига.
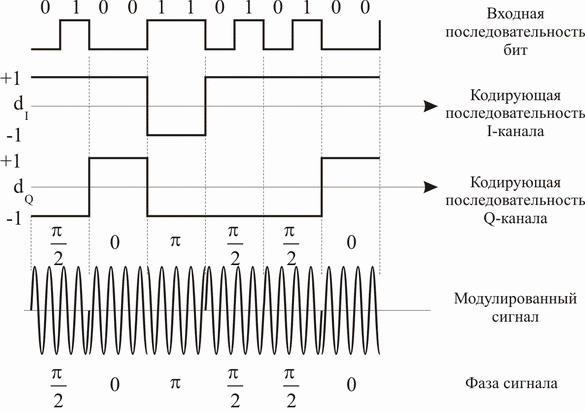
Теперь за раз мы можем кодировать 2 бита. То есть скорость передачи возрастает вдвое. Но и вероятность ошибки при тоже неизбежно возрастет.
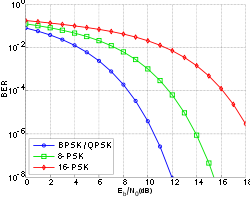
Аналогичным образом можно получить большее число фазовых сдвигов. Возможные состояния сигнала обычно показывают на векторной диаграмме или на плоскости сигнального созвездия
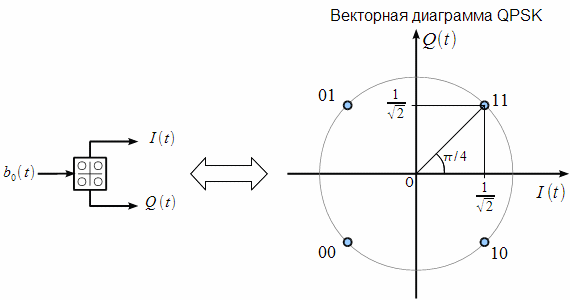
Обратите внимание, что последовательность бинарных слов на диаграмме представляет собой Код Грея, что минимизирует вероятность ошибки. Кроме того — есть дополнительный сдвиг на 45 градусов — это делается для того, чтобы уменьшить паразитную амплитудную модуляцию при скачках фазы на 180 градусов
На практике синхронный способ передачи не используется — потому что есть привязка к какой то начальной фазе, а со временем набегает ошибка и фаза уплывает, нужно постоянно переустанавливать начальную фазу — синхронизировать приемник и передатчик. Поэтому носителем информации в реальных системах является не фаза, а изменение фазы — дифференциальный способ передачи сигнала позволяет избавиться от синхронизации. Например при каждом появлении нуля — фаза делает скачок на 180 градусов (BPSK).
Далее уже можно начать говорить о тонкостях реализации — как всегда — на практике все оказывается сложнее, чем в теории, данная статья — скорее небольшой ликбез для расширения кругозора.
UPD Отличное наглядное видео про квадратурную модуляцию