
Привет, %username%!
В сегодняшнем посте речь пойдет о криптостойкости генераторов псевдослучайных чисел (ГПСЧ).
Для начала определимся, что же такое криптостойкий ГПСЧ (КСГПСЧ).
КСГПСЧ должен удовлетворять «тесту на следующий бит». Смысл теста в следующем: не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 битов с вероятностью более 50 %.Wikipedia
Возможно, кое-кто из читателей использовал такие ГПСЧ, как регистры сдвига с линейной обратной связью (РСЛОС) или любимый многими программистами Вихрь Мерсенна. Я постараюсь показать, что оба этих способа, несмотря на весьма хорошие статистические свойства и большие периоды, не соответствуют приведенному выше определению и их нельзя считать криптографически стойкими, а также предложу, в качестве альтернативы, два очень надежных ГПСЧ.
Регистр сдвига с линейной обратной связью
Часто доводилось видеть как этот метод предлагали использовать в криптографических целях, поэтому, с него, собственно, и начнем. Такого рода генераторы состоят из сдвигового регистра и функции обратной связи.
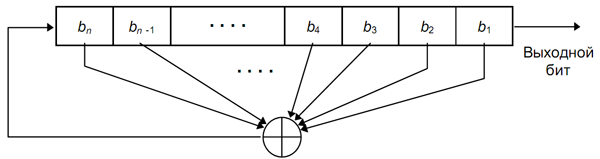
Каждый ГПСЧ на РСЛОС связан с определенным многочленном, который характеризует длину регистра и функцию обратной связи. К примеру, многочлену
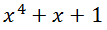 соответствует следующий регистр:
соответствует следующий регистр: 
Степень многочлена задает длину регистра, ненулевые члены описывают какие элементы регистра составляют отводную последовательность.
Если многочлен образующий отводную последовательность является неприводимым по модулю 2, тогда период генерируемой регистром последовательности будет максимальным и вычисляется по формуле
 .
.Перед началом работы в регистр заносится произвольная последовательность бит, которая называется начальным состоянием. После чего каждый такт генератора возвращает 1 бит, выглядящий совершенно случайным.
Сами по себе РСЛОС являются хорошими ГПСЧ, но в силу того, что полученные с их помощью биты имеют линейную связь использовать РСЛОС в криптографических целях неразумно.
Если злоумышленник получит последовательность бит длиной n, сгенерированную с помощью РСЛОС он может загрузить эти биты в регистр и прокрутив его назад получит начальное состояние. Знание начального состояния даст ему доступ ко всем сгенерированным раннее и генерируемым в будущем последовательностям.
Хорошей идеей может показаться скрытие информации о регистре. Тогда, даже получив последовательность длиной n атакующий не сможет предпринять шагов по вскрытию начального состояния.
Но такая ситуация легко решается с помощью алгоритма Berlekamp–Massey. Данный алгоритм позволяет вскрыть связанные с РСЛОС многочлен. Для этого достаточно иметь сгенерированную регистром последовательность длиной всего 2n.
Алгоритм достаточно прост в реализации:
public int[] BerlekampMassey(int[] array)
{
int N = array.Length;
int[] b = new int[N];
int[] c = new int[N];
int[] t = new int[N];
b[0] = 1;
c[0] = 1;
int l = 0;
int m = -1;
for (int n = 0; n < N; n++)
{
int d = 0;
for (int i = 0; i <= l; i++)
{
d ^= c[i] * array[n - i];
}
if (d == 1)
{
Array.Copy(c, 0, t, 0, N);
int N_M = (n-m);
for (int j = 0; j < N - N_M; j++)
{
c[N_M + j] ^= b[j];
}
if (l <= n / 2)
{
l = n + 1 - l;
m = n;
Array.Copy(t, 0, b, 0, N);
}
}
}
return c;
}
На вход поступает последовательность бит, сгенерированная с помощью РСЛОС. В качестве результата возвращается многочлен, характеризующий схему обратной связи.
Разумеется, РСЛОС можно объединять в каскады для более криптостойкого ГПСЧ. Эта идея используется в некоторых поточных шифрах. Однако, многие генераторы, основанные на этом способе уязвимы к так называемым корреляционным атакам. Немного подробностей об этом виде атак я приводил в своем недавнем посте Безопасность GSM сетей: шифрование данных. Здесь же скажу только, что с помощью корреляционной атаки, злоумышленник обладая последовательностью сгенерированной ГПСЧ имеет возможность восстановить начальное значение и получить доступ ко всем генерируемым в будущем значениям.
Вихрь Мерсенна
Гораздо более интересным на мой взгляд является ГПСЧ, называемый Вихрь Мерсенна. Существует несколько вариантов алгоритма, Мы рассмотрим только наиболее часто используемый MT19937. Кратко опишем этот алгоритм.
Вихрь Мерсенна состоит из двух частей: РСЛОС и закалки.

Регистр сдвига состоит из 624 элементов, каждый длиной 32 бита. Инициализация начального состояния описывается функцией:
function initialize_generator(int seed) {
index := 0
MT[0] := seed
for i from 1 to 623 { // loop over each other element
MT[i] := last 32 bits of(1812433253 * (MT[i-1] xor (right shift by 30 bits(MT[i-1]))) + i) // 0x6c078965
}
}
На вход инициализационной функции подается некое значение seed, с помощью которого осуществляется заполнение всего регистра.
На первом и каждом последующем 624-м шаге происходит перемешивание внутреннего состояния регистра:
function generate_numbers() {
for i from 0 to 623 {
int y := (MT[i] & 0x80000000) // bit 31 (32nd bit) of MT[i]
+ (MT[(i+1) mod 624] & 0x7fffffff) // bits 0-30 (first 31 bits) of MT[...]
MT[i] := MT[(i + 397) mod 624] xor (right shift by 1 bit(y))
if (y mod 2) != 0 { // y is odd
MT[i] := MT[i] xor (2567483615) // 0x9908b0df
}
}
}
На каждом шаге алгоритм возвращает следующее число из текущего состояния регистра и производит так называемую «закалку»:
function extract_number() {
if index == 0 {
generate_numbers()
}
int y := MT[index]
//закалка
y := y xor (right shift by 11 bits(y))
y := y xor (left shift by 7 bits(y) and (2636928640)) // 0x9d2c5680
y := y xor (left shift by 15 bits(y) and (4022730752)) // 0xefc60000
y := y xor (right shift by 18 bits(y))
index := (index + 1) mod 624
return y
}
Для того чтобы получить доступ к внутреннему состоянию алгоритма атакующему достаточно получить последовательность состоящую из 624 чисел.
Все что нужно сделать это вернуть числа сгенерированные алгоритмом к состоянию, в котором они находились до этапа «закалки». Для этого необходимо проделать все шаги закалки в обратном направлении. Например, рассмотрим последний шаг закалки:
y := y ^ (y >>> 18)Давайте посмотрим что происходит с двоичными данными при выполнении этой операции:
y 10110111010111100111111001110010
y >>> 18 00000000000000000010110111010111100111111001110010
y ^ (y >>> 18) 10110111010111100101001110100101
Как видите, первые 18 бит результата и исходного числа совпадают. Для того чтобы восстановить оставшиеся 14 бит нам нужно проделать следующее действие:
result ^ (result >>> 18) Действуя аналогичным образом для всех шагов этапа закалки мы получим элемент начального состояния ГПСЧ:
private uint reverse(uint output)
{
uint tempout = output >> 18;
output = output ^ tempout;
tempout = output << 15;
output = (uint)(output ^ (tempout & 4022730752));
uint a = output << 7;
uint b = (uint)(output ^ (a & 2636928640));
uint c = b << 7;
uint d = (uint)(output ^ (c & 2636928640));
uint e = d << 7;
uint f = (uint)(output ^ (e & 2636928640));
uint g = f << 7;
uint h = (uint)(output ^ (g & 2636928640));
uint i = h << 7;
uint tempfinal = (uint)(output ^ (i & 2636928640));
uint k = tempfinal >> 11;
uint l = (uint)(tempfinal ^ k);
uint m = (uint)l >> 11;
uint final = (uint)(tempfinal ^ m);
return final;
}
Как я уже отмечал выше, если атакующий имеет 624 числа сгенерированных с помощью Вихря Мерсенна этого достаточно для того чтобы восстановить все внутреннее состояние и предугадывать с вероятностью 100% все генерируемые в последующем числа.
Криптостойкие ГПСЧ
В качестве альтернативы я хочу предложить два очень надежных метода.
Алгоритм Blum — Blum — Shub
Данный генератор основан на сложности решения задачи факторизации больших чисел.
Алгоритм генерирует последовательность псевдослучайных бит и состоит из следующих шагов:
- Сгенерировать два больших простых числа p, q, таких, что p=q=3 mod 4.
- Вычислить M = p*q.
- Взять большое число x0, взаимно простое с M.
- На каждом шаге генерации последовательности вычисляется число xi+1 = xi2 mod M.
- В качестве результата возвращается последний бит числа xi.
На сегодняшний день этот алгоритм является, пожалуй, наиболее надежным ГПСЧ. Для вскрытия начального состояния или угадывания следующего элемента псевдослучайной последовательности атакующий должен знать числа p и q.
У генератора BBS есть только один недостаток — это крайне низкая скорость. Для увеличения производительности на каждом шаге генерации можно возвращать вместо одного, log(log M) бит. Это позволит увеличить скорость не снижая криптостойкости.
Режим шифрования CTR
Более быстрым, но столь же надежным способ получения псевдослучайной последовательности является CTR режим шифрования блочных шифров, другими словами режим счетчика. В качестве шифрующей функции можно использовать любой стойкий блочный шифр, к примеру AES.

На вход шифрующей функции подается ключ шифрования и блок данных размеров 128 бит, состоящий из случайной битовой строки и счетчика. На каждом шаге счетчик увеличивается на единицу, гарантируя тем самым неповторяющуюся последовательность блоков. Генерируемая последовательность состоит из зашифрованных блоков. Для того чтобы предугадать следующий элемент генерируемой последовательности злоумышленнику необходимо вскрыть ключ шифрования, т.е. задача сводится ко взлому используемого в схеме блочного шифра.
Заключение
Прежде всего, я хотел продемонстрировать криптографическую ненадежность таких хорошо зарекомендовавших себя ГПСЧ, как регистры с линейной обратной связью и Вихрь Мерсенна.
Оба эти алгоритма выгодно отличает большая скорость работы. Они генерируют по настоящему хорошие последовательности, статистически неотличимые от случайных. Но, к сожалению, когда речь заходит о криптографии этого зачастую бывает недостаточно и необходимо использовать более медленные, но куда более защищенные методы.