Признаки Хаара, про которые я расскажу, известны большинству людей, которые так или иначе связаны с системами распознавания и машинного обучения, но, судя по всему, мало кто использует их для решения задач вне стандартной области применения. Статья посвящена применению каскадов Хаара для сравнения близких изображений, в задачах сопровождение объекта между соседними кадрами видео, поиска соответствия на нескольких фотографиях, поиска образа на изображении и прочих подобных задач.
NB!
Обратите внимание, статья 2011 года. А сейчас 2021. С тех пор произошло пару революций в ComputerVision. Сейчас каскады Хаара не быстрее нейронных сетей. Не точнее. Их никто не поддерживает, и.т.д., и.т.п. Что делать, что использовать? Бесполезно делать «универсальный» гайд. Ситуация может поменяться за пол года. Из последнего — вот мое видео как выбирать хорошую модель:
А так, я часто пишу на своем канале (vk, telegram) про более новые методы/подходы.
Но, если вы хотите истории, то поехали

В большинстве случаев, когда нужно простое сравнение двух достаточно похожих фрагментов изображения его реализуют через их ковариацию (или что-нибудь аналогичное). Берётся образец (на фотографии — цветок) и передвигается по изображению по X и Y в поисках точки, где отличие образца (J) от изображения (I):
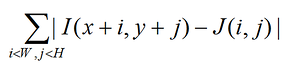
достигает своего минимума.
Этот способ очень быстр в реализации, интуитивен и досконально известен. Пожалуй я не встречал ни единой группы разработчиков, где бы его не использовали. Конечно, все замечательно знают его недостатки:
- Неустойчивость при смене освещения
- Неустойчивость при изменении масштаба или повороте изображения
- Неустойчивость, если часть изображения — изменяющийся фон
- Маленькая скорость работы — если нужно обнаружить область n*n на изображении m*m, то количество операций будет пропорционально n2∙(m-n)2.
Как бороться с этими недостатками все тоже знают.
- Освещение нейтрализуется нормировкой или переходом к бинаризации области.
- Изменения масштаба и небольшие повороты нейтрализуются изменением разрешения при корреляции.
- С фоном при таком подходе никто не борется.
- Скорость оптимизируют путём поиска с большим шагом или при маленьком разрешении.
В ситуациях, когда результатов корреляции недостаточно — переходят к более сложным методам, таким как сравнению карт особых точек (SURF), границ, или непосредственному выделению объектов. Но эти алгоритмы совсем о другом: в большинстве случаев они достаточно медленные, их сложно написать с нуля (особенно на каком-нибудь DSP-процессоре), есть ограничения на структуру изображения.
В какой-то момент, обдумывая очередной проект, упёрся в задачку где требовалось сравнить несколько изменчивых областей в изображении. И думал, пока мне не вспомнился однажды упомянутый на Хабре алгоритм Predator, где было показано быстрое и устойчивое ведение объекта в видео. Немножко поразмыслив, я понял, что весь этот подход, позволяющий решать большой класс задач прошёл мимо меня.
Напомню, что такое признаки Хаара. Каскады из признаков обычно упоминаются как база для построения систем выделения сложных объектов, таких как лица, руки, или другие предметы. В большинстве статей этот подход неразрывно связывают с алгоритмом обучения AdaBoosta. Сам по себе каскад Хаара — это набор примитивов, для которых считается их свёртка с изображением. Используются самые простые примитивы, состоящих из прямоугольников и имеющих всего два уровня, +1 и -1. При этом каждый прямоугольник используется несколько раз разного размера. Под свёрткой тут подразумевается s = X-Y, где Y — сумма элементов изображения в тёмной области, а X — сумма элементов изображения в светлой области ( можно так же брать X/Y, тогда будет устойчивость при изменении масштаба).

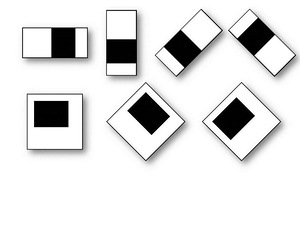
Такие свёртки подчёркивают структурную информацию объекта: например для центра лица человека будет всегда отрицательна следующая свёртка:


Глаза будут темнее, чем область между ними, так же как область рта будет темнее чем лоб. Чем больше используется различных примитивов, тем точнее можно потом классифицировать объект. При этом если точная классификация не нужна — можно использовать меньшее количество примитивов.
Тут можно упомянуть, что в задаче распознавания объектов, после того, как построены наборы признаков по тестовой выборке, алгоритмы обучения (AdaBoost, SVM) определяют последовательность (каскад) свёрток, соответствующих объекту. При распознавании объекта на изображении производиться его сравнение с тестовым изображением.
В чём же плюс Хаара и почему нельзя использовать вместо этих уродских прямоугольничков такие замечательные и физичные кривые как, например, синусоиды и гауссианы?
Плюс в том, что каскады Хаара очень быстро считаются через интегральное представление изображений. Более подробно это описано по ссылке, а тут я лишь кратко скажу, что интегральное изображение представляется как:
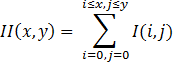
Значение в точке X,Y матрицы (II), полученной из исходного изображения (I) это сумма всех точек в прямоугольнике (0,0,X,Y). Тогда интеграл по любому прямоугольнику (ABCD) в изображении представим как:
SumOfRect(ABCD) = II(A) + II(С) — II(B) — II(D)
Что даёт всего лишь 4 обращения к памяти и 3 математических действия для подсчёта суммы всех элементов прямоугольника вне зависимости от его размера. При расчёте других свёрток, отличных от свёрток примитивов Хаара, требуется количество действий пропорциональное квадрату размера примитива (если не рассчитывать через БПФ, что возможно не для любых паттернов).
Вернёмся к нашей задачке. Пусть мы хотим найти небольшой фрагмент (J) в большом изображении (I). Для того, чтобы это сделать не требуется обучение. По одному фрагменту всё равно невозможно его произвести. Примитивы Хаара помогут получить образ J и искать на I именно его. Достаточно получить свёртки J с набором Хаар-признаков и сравнить с набором свёрток тех же примитивов, рассчитанных на I в окнах пропорциональных небольшому фрагменту.
Плюсы:
- Устойчивость к смене освещения, даже если это локальная смена освещения, устойчивость к шумам (примитивы представляют собой простейший полосовой фильтр).
- Если примитивы были не очень маленькие, то сильно устойчивее корреляции при изменении масштаба(размер примитивов при этом не будет влиять на точность, если обход с маленьким шагом).
- Если признаки на большом изображении рассчитать заранее и при сдвиге окна поиска брать уже посчитанные и актуальные для него — поиск будет значительно быстрее корреляции (нужно сравнить меньшее количество элементов).
При этом видно, что можно провести ряд достаточно простых оптимизаций, которые ускорят и уточнят этот подход.
Если кому-то захотелось поиграться, я написал небольшую программку, в которой реализован самый простой вариант этого алгоритма. В программе осуществляется ведение выбранного фрагмента в видеопотоке. EmguCV для подцепления камеры и простых преобразований изображения (Хаар делается вручную).