
Все отлично знают, что из класса обменных сортировок самый быстрый метод – это так называемая быстрая сортировка. О ней пишут диссертации, её посвящено немало статей на Хабре, на её основе придумывают сложные гибридные алгоритмы. Но сегодня речь пойдёт не про quick sort, а про другой обменный способ – старую добрую пузырьковую сортировку и её улучшения, модификации, мутации и разновидности.
Практический выхлоп от данных методов не ахти какой и многие хабрапользователи всё это проходили ещё в первом классе. Поэтому статья адресована тем, кто только-только заинтересовался теорией алгоритмов и делает в этом направлении первые шаги.
image: пузырьки
Сегодня поговорим о простейших сортировках обменами.
Если кому интересно, скажу, что есть и другие классы – сортировки выбором, сортировки вставками, сортировки слиянием, сортировки распределением, гибридные сортировки и параллельные сортировки. Есть, кстати, ещё эзотерические сортировки. Это различные фейковые, принципиально нереализуемые, шуточные и прочие псевдо-алгоритмы, про которые я в хабе «IT-юмор» как-нибудь напишу пару статей.
Но к сегодняшней лекции это не имеет отношения, нас сейчас интересуют только простенькие сортировки обменами. Самих сортировок обменами тоже немало (я знаю более дюжины), поэтому мы рассмотрим так называемую пузырьковую сортировку и некоторые другие, с ней тесно взаимосвязанные.
Заранее предупрежу, что почти все приведённые способы весьма медленные и глубокого анализа их временной сложности не будет. Какие-то побыстрее, какие-то помедленнее, но, грубо говоря, можно сказать, что в среднем O(n2). Также я не вижу резона загромождать статью реализациями на каких-либо языках программирования. Заинтересовавшиеся без малейшего труда смогут найти примеры кода на Розетте, в Википедии или где-нибудь ещё.
Но вернёмся к сортировкам обменами. Упорядочивание происходит в результате многократного последовательного перебора массива и сравнения пар элементов между собой. Если сравниваемые элементы не отсортированы друг относительно друга – то меняем их местами. Вопрос только в том, каким именно макаром массив обходить и по какому принципу выбирать пары для сравнения.
Начнём не с эталонной пузырьковой сортировки, а с алгоритма, который называется…
Глупая сортировка
Сортировка и впрямь глупейшая. Просматриваем массив слева-направо и по пути сравниваем соседей. Если мы встретим пару взаимно неотсортированных элементов, то меняем их местами и возвращаемся на круги своя, то бишь в самое начало. Снова проходим-проверяем массив, если встретили снова «неправильную» пару соседних элементов, то меняем местами и опять начинаем всё сызнова. Продолжаем до тех пор пока массив потихоньку-полегоньку не отсортируется.

«Так любой дурак сортировать умеет» — скажете Вы и будете абсолютно правы. Именно поэтому сортировку и прозвали «глупой». На этой лекции мы будем последовательно совершенствовать и видоизменять данный способ. Сейчас у него временная сложность O(n3), произведя одну коррекцию, мы уже доведём до O(n2), потом ускорим ещё немного, потом ещё, а в конце концов мы получим O(n log n) – и это будет вовсе не «Быстрая сортировка»!
Внесём в глупую сортировку одно-единственное улучшение. Обнаружив при проходе два соседних неотсортированных элемента и поменяв их местами, не станем откатываться в начало массива, а невозмутимо продолжим его обход до самого конца.
В этом случае перед нами не что иное как всем известная…
Пузырьковая сортировка
Или сортировка простыми обменами. Бессмертная классика жанра. Принцип действий прост: обходим массив от начала до конца, попутно меняя местами неотсортированные соседние элементы. В результате первого прохода на последнее место «всплывёт» максимальный элемент. Теперь снова обходим неотсортированную часть массива (от первого элемента до предпоследнего) и меняем по пути неотсортированных соседей. Второй по величине элемент окажется на предпоследнем месте. Продолжая в том же духе, будем обходить всё уменьшающуюся неотсортированную часть массива, запихивая найденные максимумы в конец.

Если не только в конец задвигать максимумы, а ещё и в начало перебрасывать минимумы то у нас получается…
Шейкерная сортировка
Она же сортировка перемешиванием, она же коктейльная сортировка. Начинается процесс как в «пузырьке»: выдавливаем максимум на самые задворки. После этого разворачиваемся на 1800 и идём в обратную сторону, при этом уже перекатывая в начало не максимум, а минимум. Отсортировав в массиве первый и последний элементы, снова делаем кульбит. Обойдя туда-обратно несколько раз, в итоге заканчиваем процесс, оказавшись в середине списка.

Шейкерная сортировка работает немного быстрее чем пузырьковая, поскольку по массиву в нужных направлениях попеременно мигрируют и максимумы и минимумы. Улучшения, как говорится, налицо.
Как видите, если к процессу перебора подойти творчески, то выталкивание тяжёлых (лёгких) элементов к концам массива происходит быстрее. Поэтому умельцы предложили для обхода списка ещё одну нестандартную «дорожную карту».
Чётно-нечётная сортировка
На сей раз мы не будем сновать по массиву взад-вперёд, а снова вернёмся к идее планомерного обхода слева-направо, но только сделаем шире шаг. На первом проходе элементы с нечётным ключом сравниваем с соседями, зиждущимися на чётных местах (1-й сравниваем со 2-м, затем 3-й с 4-м, 5-й с 6-м и так далее). Затем наоборот – «чётные по счёту» элементы сравниваем/меняем с «нечётными». Затем снова «нечёт-чёт», потом опять «чёт-нечет». Процесс останавливается тогда, когда после подряд двух проходов по массиву («нечётно-чётному» и «чётно-нечётному») не произошло ни одного обмена. Стало быть, отсортировали.

В обычном «пузырьке» во время каждого прохода мы планомерно выдавливаем в конец массива текущий максимум. Если же передвигаться вприпрыжку по чётным и нечётным индексам, то сразу все более-менее крупные элементы массива одновременно за один пробег проталкиваются вправо на одну позицию. Так получается быстрее.
Разберём последнее покращення* для Сортування бульбашкою** — Сортування гребінцем***. Этот способ упорядочивает весьма шустро, O(n2) – его наихудшая сложность. В среднем по времени имеем O(n log n), а лучшая даже, не поверите, O(n). То есть, весьма достойный конкурент всяким «быстрым сортировкам» и это, заметьте, без использования рекурсии. Впрочем, я обещал, что в крейсерские скорости мы сегодня углубляться не станем, засим умолкаю и перехожу непосредственно к алгоритму.

Во всём виноваты черепашки
Небольшая предыстория. В 1980 году Влодзимеж Добосиевич пояснил почему пузырьковая и производные от неё сортировки работают так медленно. Это всё из-за черепашек. «Черепахи» — небольшие по значению элементы, которые находятся в конце списка. Как Вы, возможно, заметили пузырьковые сортировки ориентированы на «кроликов» (не путать с «кроликами» Бабушкина) – больших по значению элементов в начале списка. Они весьма резво перемещаются к финишу. А вот медлительные пресмыкающиеся на старт ползут неохотно. Подгонять «тортилл» можно с помощью расчёски.
image: виноватая черепашка
Сортировка расчёской
В «пузырьке», «шейкере» и «чёт-нечете» при переборе массива сравниваются соседние элементы. Основная идея «расчёски» в том, чтобы первоначально брать достаточно большое расстояние между сравниваемыми элементами и по мере упорядочивания массива сужать это расстояние вплоть до минимального. Таким образом мы как бы причёсываем массив, постепенно разглаживая на всё более аккуратные пряди.

Первоначальный разрыв между сравниваемыми элементами лучше брать не абы какой, а с учётом специальной величины называемой фактором уменьшения, оптимальное значение которой равно примерно 1,247. Сначала расстояние между элементами равно размеру массива разделённого на фактор уменьшения (результат, естественно, округляется до ближайшего целого). Затем, пройдя массив с этим шагом, мы снова делим шаг на фактор уменьшения и проходим по списку вновь. Так продолжается до тех пор, пока разность индексов не достигнет единицы. В этом случае массив досортировывается обычным пузырьком.
Опытным и теоретическим путём установлено оптимальное значение фактора уменьшения:
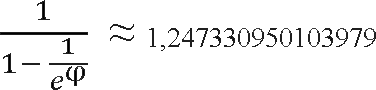
Когда был изобретён этот метод, на него на стыке 70-х и 80-х мало кто обратил внимание. Десятилетие спустя, когда программирование перестало быть уделом учёных и инженеров IBM, а уже лавинообразно набирало массовый характер, способ переоткрыли, исследовали и популяризировали в 1991 году Стивен Лейси и Ричард Бокс.
Вот собственно и всё что я хотел Вам рассказать про пузырьковую сортировку и иже с ней.
— Примечания
* покращення (укр.) – улучшение
** Сортування бульбашкою (укр.) – Сортировка пузырьком
*** Сортування гребінцем (укр.) – Сортировка расчёской
Only registered users can participate in poll. Log in, please.
Какие алгоритмы из этой статьи Вы уже знали?
57.1% Глупая сортировка772
91.27% Пузырьковая сортировка1234
39.79% Шейкерная сортировка538
15.46% Чётно-нечётная сортировка209
17.09% Сортировка расчёской231
1352 users voted. 283 users abstained.