Требуемые знания: знакомство с методами линейного программирования, методы решения транспортной задачи(особенно метод потенциалов).
Год назад, на третьем
курсе в качестве одной из лабораторных работ по курсу «Методы оптимизации» мне задали реализовать решение транспортной задачи, но с одним небольшим условием: перевозки происходят партиями. Это значит, что теперь, в отличие от классической постановки, оплачивается перевозка партии товаров (e.g. 10 штук), и, даже если Вам надо перевезти 11 штук, Вы заплатите за две партии(в один трейлер 11 штук не влезут). Казалось бы, мелкое дополнение, однако как теперь решать задачу, да хотя бы как её формализовать? Как студенту кафедры прикладной математики, мне было не привыкать, что великий google.ru чего-то не знает, но каково же было моё удивление, когда ни его старший брат — англоязычный google, ни тьма перебранных мной книг по теории оптимизации не смогли ответить на этот вопрос.
Сразу хочу сказать — на премию Филдса я со своим алгоритмом не претендую. Ничего сверхъестественного я не предлагаю, но тем, кто только приступает к решению такой задачи, могу немного подсобить.
Пусть C — платёжная матрица, a — вектор запасов груза, b — вектор потребности в грузе, k — количество товаров в партии. Будем рассматривать такую формализацию:
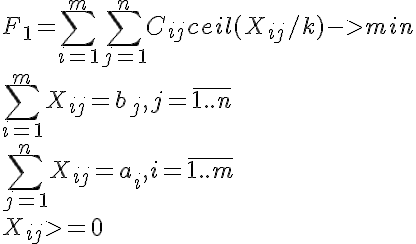
где X — матрица перевозок, т.е. оптимизируемый параметр, а ceil — округление вверх до ближайшего целого.
Дополнительно введём в рассмотрение:
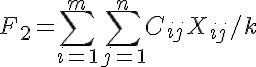
Для начала решаем классическую транспортную задачу с F2->min. Полученное значение F2 является нижней границей для F1 на множестве допустимых значений. Запомним значение F2_save:=F2. Находим значение F1 при полученном решении X и запомним его F1_save=F1. Если F1_save==ceil(F2_save), то X — искомое решение, в противном случае идём далее.
F1 можно уменьшить лишь уменьшая базисные компоненты X до ближайших кратных k значений, поэтому будем строить(метод ветвей и границ) дерево решений задач с дополнительными ограничениями. Вершиной дерева является уже полученное решение. Каждый следующий ярус дерева строится следующим образом: для каждой базисной компоненты(xij), равной некоторому не кратному k значению(z), решаем классическую транспортную задачу F2->min с дополнительным ограничением xij=[z/k]*k ([x] — целая часть от x) (см. P.S.). Если для полученного решения F1<F1_save, то F1_save:=F1. Если для полученного решения ceil(F2)>=F1_save, то далее эту ветвь не продолжаем. Если F1==ceil(F2_save), то полученное X — искомое решение, в противном случае идём далее. Таким образом получаем дерево решений, каждая ветвь которого завершается если на листе этой ветви ceil(F2)>=F1_save, или если все компоненты из базиса кратны k или если задача вообще не имела решение. План, соответствующий полученному после построения дерева F1_save, является оптимальным.
P.S. Добавляя ограничение не обязательно решать задачу заново. Можно, например, перебрать все возможные уменьшающие F1 циклы и выбрать среди них оптимальный. Или воспользоваться методами двойственного симплекс метода.
Example
Рассмотрим алгоритм на очень простом примере. Пусть k=3, С={{2,2},{4,5}}, a={2,3}, b={2,3}. Итак вершина дерева — решение такой транспортной задачи с целевой функцией F2:
0) X={{0,2},{2,1}}, F2(X)~=5.67, F1(X)=2+4+5=11.
F2_save:=5.67, F1_save:=11
т.к. ceil(5.67)<11 идём далее — строим следующий ярус дерева:
1.1) к решаемой в узле 0 задаче добавляем условие x12==0 и решаем её снова.
X={{2,0},{0,3}}, F2(X)~=6.35, F1(X)=2+5=7.
т.к. F1<F1_save (7<11), то F1_save:=7
т.к. ceil(F2)>=F1_save (7>=7), то далее эту ветвь не продолжаем
т.к. F1>ceil(F2_save) идём далее(возможно существует решение лучше), ветвь не продолжается, но ярус ещё не закончен.
1.2) к решаемой в узле 0 задаче добавляем условие x21==0 и решаем её снова.
X={{2,0},{0,3}}, F2(X)~=6.35, F1(X)=2+5=7.
т.к. F1==F1_save (7==7), то F1_save не изменяется
т.к. ceil(F2)>=F1_save (7>=7), то далее эту ветвь не продолжаем
т.к. F1>ceil(F2_save) идём далее(возможно существует решение лучше), ветвь не продолжается, но ярус ещё не закончен.
1.3) к решаемой в узле 0 задаче добавляем условие x22==0 и решаем её снова. Такая задача не имеет решения => и эту ветвь мы не продолжаем.
Базисных компонент больше не осталось(ярус закончен) и ветви продолжать не надо(бессмысленно, лучше решение мы не получим), значит дерево построено. F1_save==7 — это наши минимальные затраты. План им соответствующий(он же ответ) X={{2,0},{0,3}}
Год назад, на третьем
курсе в качестве одной из лабораторных работ по курсу «Методы оптимизации» мне задали реализовать решение транспортной задачи, но с одним небольшим условием: перевозки происходят партиями. Это значит, что теперь, в отличие от классической постановки, оплачивается перевозка партии товаров (e.g. 10 штук), и, даже если Вам надо перевезти 11 штук, Вы заплатите за две партии(в один трейлер 11 штук не влезут). Казалось бы, мелкое дополнение, однако как теперь решать задачу, да хотя бы как её формализовать? Как студенту кафедры прикладной математики, мне было не привыкать, что великий google.ru чего-то не знает, но каково же было моё удивление, когда ни его старший брат — англоязычный google, ни тьма перебранных мной книг по теории оптимизации не смогли ответить на этот вопрос.Сразу хочу сказать — на премию Филдса я со своим алгоритмом не претендую. Ничего сверхъестественного я не предлагаю, но тем, кто только приступает к решению такой задачи, могу немного подсобить.
Пусть C — платёжная матрица, a — вектор запасов груза, b — вектор потребности в грузе, k — количество товаров в партии. Будем рассматривать такую формализацию:
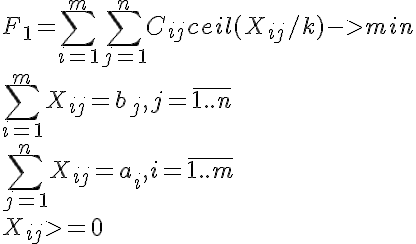
где X — матрица перевозок, т.е. оптимизируемый параметр, а ceil — округление вверх до ближайшего целого.
Дополнительно введём в рассмотрение:
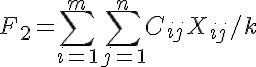
Для начала решаем классическую транспортную задачу с F2->min. Полученное значение F2 является нижней границей для F1 на множестве допустимых значений. Запомним значение F2_save:=F2. Находим значение F1 при полученном решении X и запомним его F1_save=F1. Если F1_save==ceil(F2_save), то X — искомое решение, в противном случае идём далее.
F1 можно уменьшить лишь уменьшая базисные компоненты X до ближайших кратных k значений, поэтому будем строить(метод ветвей и границ) дерево решений задач с дополнительными ограничениями. Вершиной дерева является уже полученное решение. Каждый следующий ярус дерева строится следующим образом: для каждой базисной компоненты(xij), равной некоторому не кратному k значению(z), решаем классическую транспортную задачу F2->min с дополнительным ограничением xij=[z/k]*k ([x] — целая часть от x) (см. P.S.). Если для полученного решения F1<F1_save, то F1_save:=F1. Если для полученного решения ceil(F2)>=F1_save, то далее эту ветвь не продолжаем. Если F1==ceil(F2_save), то полученное X — искомое решение, в противном случае идём далее. Таким образом получаем дерево решений, каждая ветвь которого завершается если на листе этой ветви ceil(F2)>=F1_save, или если все компоненты из базиса кратны k или если задача вообще не имела решение. План, соответствующий полученному после построения дерева F1_save, является оптимальным.
P.S. Добавляя ограничение не обязательно решать задачу заново. Можно, например, перебрать все возможные уменьшающие F1 циклы и выбрать среди них оптимальный. Или воспользоваться методами двойственного симплекс метода.
Example
Рассмотрим алгоритм на очень простом примере. Пусть k=3, С={{2,2},{4,5}}, a={2,3}, b={2,3}. Итак вершина дерева — решение такой транспортной задачи с целевой функцией F2:
0) X={{0,2},{2,1}}, F2(X)~=5.67, F1(X)=2+4+5=11.
F2_save:=5.67, F1_save:=11
т.к. ceil(5.67)<11 идём далее — строим следующий ярус дерева:
1.1) к решаемой в узле 0 задаче добавляем условие x12==0 и решаем её снова.
X={{2,0},{0,3}}, F2(X)~=6.35, F1(X)=2+5=7.
т.к. F1<F1_save (7<11), то F1_save:=7
т.к. ceil(F2)>=F1_save (7>=7), то далее эту ветвь не продолжаем
т.к. F1>ceil(F2_save) идём далее(возможно существует решение лучше), ветвь не продолжается, но ярус ещё не закончен.
1.2) к решаемой в узле 0 задаче добавляем условие x21==0 и решаем её снова.
X={{2,0},{0,3}}, F2(X)~=6.35, F1(X)=2+5=7.
т.к. F1==F1_save (7==7), то F1_save не изменяется
т.к. ceil(F2)>=F1_save (7>=7), то далее эту ветвь не продолжаем
т.к. F1>ceil(F2_save) идём далее(возможно существует решение лучше), ветвь не продолжается, но ярус ещё не закончен.
1.3) к решаемой в узле 0 задаче добавляем условие x22==0 и решаем её снова. Такая задача не имеет решения => и эту ветвь мы не продолжаем.
Базисных компонент больше не осталось(ярус закончен) и ветви продолжать не надо(бессмысленно, лучше решение мы не получим), значит дерево построено. F1_save==7 — это наши минимальные затраты. План им соответствующий(он же ответ) X={{2,0},{0,3}}
