В этой статье я постараюсь максимально доходчиво рассказать о таком простом, но эффективном методе оптимизации, как имитация отжига (simulated annealing). А чтобы не быть причисленным к далёким от практики любителям теоретизировать, я покажу как применить этот метод для решения задачи коммивояжёра.
Для понимания статьи Вам понадобятся минимальные навыки программирования и владение математикой на уровне 9 класса средней школы. Статья рассчитана на людей не знакомых с методами оптимизации или только делающих первые шаги в этом направлении.
Чтобы максимально расширить круг читателей, мне пришлось почти полностью отказаться от формальных определений и сознательно пойти на некоторые не совсем точные упрощения. Надеюсь, что с водой я не выплеснул ребёнка (а если это произошло, то буду рад вашим замечаниям).
Для того, чтобы понять, что такое оптимизация, стоит сначала узнать, для чего она нужна. Сразу скажу, что с «задачами оптимизации» в повседневной жизни мы сталкиваемся с завидной регулярностью, не отдавая себе в этом отчёта.
Допустим, мы, получив очередную зарплату, решаем подбить семейный бюджет. Нужно распределить деньги так, чтобы в первую очередь удовлетворить самые важные потребности (еда, плата за электричество, интернет и т.д.), а остаток можно спустить на что-нибудь приоритетом пониже. Купить на все деньги дизайнерский телефон и умереть от голода – не самое лучшее решение, не находите?
Или другой вариант, мы решили отправиться в поход и собираем ранец. Одна проблема – вещей очень много, а ранец у нас не слишком большой (да и сами мы имеем ограниченную грузоподъёмность). Мы хотим взять как можно больше наиболее важных для нас предметов. Если мы идём в горы, прихватить с собой страховочный трос – хорошее решение, взять вместо него любимую PlayStation Vita, а остальное место забить печеньками – наверное, не очень.
Так что же делает оптимизация? Она ищет то самое, хорошее решение. Возможно, не самое лучшее из всех, но точно хорошее.
Теперь чуточку формальнее. Если заглянуть в википедию, можно без труда найти вот такое определение:
Оптимальное (от лат. optimus — наилучшее) решение — решение, которое по тем или иным признакам предпочтительнее других. Следовательно, оптимизация – это способ нахождения оптимального решения.
Теперь, давайте представим, что мы можем измерить насколько хорошее наше решение. Например, в случае «задачи про ранец», каждой вещи присвоим натуральное число (чем больше число, тем важнее вещь). Тогда наша задача приобретает уже более чёткую постановку: мы хотим заполнить ранец такими вещами, суммарный приоритет которых будет максимален, а вес не превысит определенного значения. Т.е. мы ищем максимум некоторой функции, которую принято называть целевой.
Чтобы свести всё к единому знаменателю, снова заглянем в википедию:
Оптимизация (математика) — нахождение экстремума (минимума или максимума) целевой функции в некоторой области.
Теперь, когда мы более-менее определились, с тем, что делает оптимизация, появляется резонный вопрос – «Как?».
Конечно, мы можем особо не заморачиваться и перебрать все-все решения, а затем сравнить их. В случае с ранцем, нам, наверное, даже это удастся проделать. Но теперь давайте представим, что наш ранец – вовсе не ранец, а целый поезд с множеством вагонов, а перевозим мы разные товары в другой город. Задача не изменилась (загрузить как можно больше ценного), а целевой функцией будет суммарная стоимость товаров. Сколько времени уйдёт у нас на полный перебор решений? Думаю, что много.
Можно выбирать решения случайно. Допустим, сто каких-нибудь решений, а затем из них взять самое лучшее. Несомненно, это будет значительно быстрее полного перебора, но кто даст гарантию, что наше итоговое решение будет сколько-нибудь близко к экстремуму?
Не буду томить и скажу, что методов оптимизации существует великое множество. Настолько много, что их принято разбивать на классы, все их я перечислять не буду. Скажу лишь, что «имитация отжига» относится к классу стохастических (от греч. στοχαστικός — «умеющий угадывать») или вероятностных методов. А причём здесь вероятность и как она поможет отыскать решение – чуть ниже.
Как и всё гениальное, данный метод подсмотрен у матушки природы. За основу взят процесс кристаллизации вещества, который в свою очередь «приручили» хитрые металлурги, для повышения однородности металла.
Напомню, что у каждого металла есть кристаллическая решетка, если совсем коротко, она описывает геометрическое положение атомов вещества. Совокупность позиций всех атомов будем называть состоянием системы, каждому состоянию соответствует определенный уровень энергии. Цель отжига – привести систему в состояние с наименьшей энергией. Чем ниже уровень энергии, тем «лучше» кристаллическая решетка, т.е. тем меньше у нее дефектов и прочнее металл.
В ходе «отжига» металл сначала нагревают до некоторой температуры, что заставляет атомы кристаллической решетки покинуть свои позиции. Затем начинается медленное и контролируемое охлаждение. Атомы стремятся попасть в состояние с меньшей энергией, однако, с определенной вероятностью они могут перейти и в состояние с большей. Эта вероятность уменьшается вместе с температурой. Переход в худшее состояние, как ни странно, помогает в итоге отыскать состояние с энергией меньшей, чем начальная. Процесс завершается, когда температура падает до заранее заданного значения.
Как видите, в рамках данного процесса происходит минимизация энергии. Меняем энергию на нашу целевую функцию, и voilà! Или нет? Давайте задумаемся, а чем же так хорош столь мудрёный процесс? Почему бы нам, например, всегда не переходить в состояния с меньшей энергией?
Примерно так работает имеющий широкое распространение метод градиентного спуска.
На просторах интернета мне удалось отыскать совершенно чудесную картинку, которая как нельзя лучше иллюстрирует все плюсы алгоритма.
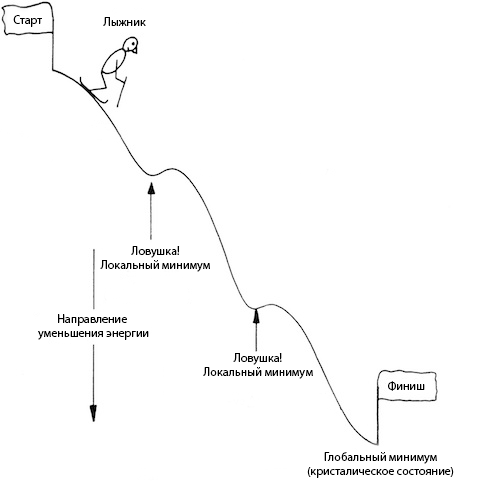
Давайте на минуточку представим себя лыжником, несущемся по крутому склону нашей целевой функции. Задача спуститься в самую нижнюю точку (глобальный минимум). Но, как видите, склон нам попался не совсем ровный, есть на нём низменности, заехав в которые, нам может показаться, что мы уже у подножья. Дабы не остаться в дураках, нам придётся проявить любопытство и вскарабкаться на небольшой холмик, чтобы продолжить спуск.
Чтобы метафора стала окончательно понятна, в примере с лыжником склон – функция измерения энергии вещества (она же целевая функция). А вероятностный переход в состояние с большей энергией – карабканье на холм справа от низменности.
Как видите, такой алгоритм позволяет нам с большой вероятностью избежать «застревания» в локальном минимуме.
Теперь мы готовы перейти к более строгому описанию метода. Введём обозначения:
Пусть S – множество всех состояний (решений) нашей задачи. Например, для задачи о ранце это будет множество всевозможных наборов вещей.
Пусть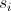 – состояние на i-м шаге алгоритма.
– состояние на i-м шаге алгоритма. 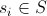 .
.
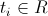 – температура на i-м шаге.
– температура на i-м шаге.
Для того, чтобы использовать имитацию отжига, нам понадобится определить три функции:
Теперь остановимся на каждой подробнее.
E каждому решению по какому-то правилу ставит в соответствие число. Зависит от конкретной задачи.
T ставит номеру итерации i в соответствие температуру. Функция определяет, как долго будет работать наш алгоритм (на самом деле она имеет более глубокое значение, но нам это знать пока не обязательно). Если T будет линейной функцией, то время работы будет относительно большим. В случае же со степенной функцией, скажем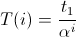 , всё закончится очень быстро, но далеко не факт, что мы не застрянем в низменности, так не добравшись до финиша.
, всё закончится очень быстро, но далеко не факт, что мы не застрянем в низменности, так не добравшись до финиша.
Для этой статьи я выбрал самый простой, линейный вариант.
Сразу оговорюсь, что весь код в этой статье был написан на Matlab. Эту среду я выбрал, так как «из коробки» можно рисовать красивые графики – не более. Писать я старался, не используя специфичной матлабной магии, чтобы код можно было легко портировать на Ваш любимый язык.
Функция F на основе предыдущего состояния порождает новое состояние-кандидат, в которое система может перейти, а может и отбросить. Обозначим его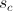 . Способ получения кандидата полностью зависит от решаемой задачи, конкретную функцию Вы сможете увидеть в примере.
. Способ получения кандидата полностью зависит от решаемой задачи, конкретную функцию Вы сможете увидеть в примере.
Теперь мы можем в самом общем виде описать алгоритм метода имитации отжига:
Как видите, всё очень просто, отдельно стоит пояснить только переход в новое состояние. Если энергия «кандидата» меньше, он становится новым состоянием, в противном случае, переход будет вероятностным (поэтому метод относят к классу стохастических).
Чтобы это точно не вызывало трудностей, я позволю себе напомнить некоторые самые базовые понятия теории вероятностей.
Неформально определим вероятность, как меру возможности наступления некоторого события. Вероятность достоверного события (событие, которое точно случится) равна единице, невозможного – нулю. Все остальные значения находятся между.
Например, при броске игральной кости вероятность выпадения любого числа равна единице, а тройки – 1/6.
В нашем случае, подставив в формулу значения разницы энергий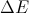 и температуры
и температуры 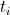 мы получим вероятность перехода. Остаётся только этот переход осуществить, но как это сделать?
мы получим вероятность перехода. Остаётся только этот переход осуществить, но как это сделать?
Код вычисления вероятности:
Давайте представим себе единичный отрезок и разобьём его на две части относительно значения нашей вероятности.
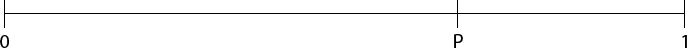
Затем воспользуемся функцией генерации равномерно распределенного случайного числа, в Matlab это rand (как и почти во всех остальных языках). Теперь отметим это число на отрезке.

Если число попало в левую часть – осуществляем переход, в правую – не делаем ничего.
Теперь, думаю, всё понятно, и мы можем перейти непосредственно к решению нашей первой задачи.
Представьте себе, что Вы странствующий торговец и хотите предложить свой товар жителям каждого города в стране. Путешествия отнимают много сил и времени, поэтому логично, что Вы хотите составить свой маршрут таким образом, чтобы расстояние, которое предстоит преодолеть, было минимальным. Этот маршрут и предстоит отыскать.
Более формально: необходимо найти кратчайший путь, проходящий через каждый город и заканчивающийся в точке отправления.
В такой постановке задача называется замкнутой задачей коммивояжёра.
Для начала давайте определимся с данными. Пусть наши города случайным образом разбросаны в квадрате 10x10. Каждый город, соответственно, представлен парой координат. Всего 100 городов.
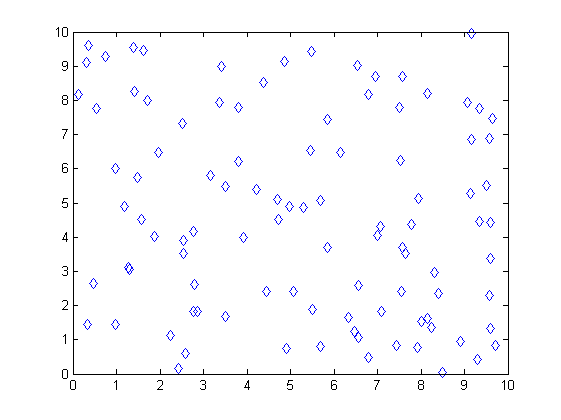
Данные можно без труда получить в Matlab при помощи следующего кода:
В других языках придётся написать цикл, но по сути это ничего не меняет. Мы генерируем случайные числа уже знакомой нам функцией rand() и домножаем их на 10, чтобы они лежали в заданной области.
Обозначим множество всех городов C, общее количество обозначается |C| и в нашем случае равно 100. Каждый город представляется как пара координат
представляется как пара координат 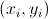 с соответствующим индексом.
с соответствующим индексом.
По условию, решением является маршрут между всеми городами, значит множество состояний S – это все возможные маршруты, проходящие через каждый город. Другими словами множество всех упорядоченных последовательностей элементов C, в которой всякий встречается ровно один раз. Очевидно, что длина каждой такой последовательности |C|.
встречается ровно один раз. Очевидно, что длина каждой такой последовательности |C|.
Как мы помним, для того, чтобы использовать метод имитации отжига мы должны определить две функции, зависящие от каждой конкретной задачи. Это функция энергии E (или «целевая функция» в общепринятой терминологии) и функция F, порождающая новое состояние.
Так как мы стремимся минимизировать расстояние, оно и будет «энергией». Следовательно, наша целевая функция будет иметь такой вид:
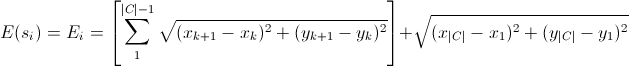
Здесь написано не что иное, как сумма Евклидовых расстояний между парами городов в маршруте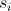 . Так как задача замкнутая, мы были вынуждены подписать
. Так как задача замкнутая, мы были вынуждены подписать 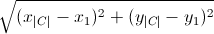 в конце, это расстояние между последним и первым городом. Если не углубляться, то Евклидово – это то самое расстояние между точками, которое мы все проходили на уроках геометрии. Задаётся оно следующей формулой:
в конце, это расстояние между последним и первым городом. Если не углубляться, то Евклидово – это то самое расстояние между точками, которое мы все проходили на уроках геометрии. Задаётся оно следующей формулой:

Где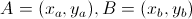
Теперь давайте подумаем, как же нам получать новое состояние? Первое что приходит в голову – менять местами два произвольных города в маршруте. Идея правильная, но такое изменение непредсказуемо влияет на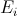 , метод будет работать долго и не факт, что успешно.
, метод будет работать долго и не факт, что успешно.
Хорошим вариантом в данном случае будет выбрать два произвольных города в маршруте и инвертировать путь между ними. Например, у нас был маршрут (1,2,3,4,5,6,7). Генератор случайных чисел выбрал города 2 и 7, мы выполнили процедуру и получили (1,7,6,5,4,3,2).
Ниже представлен код для функции F:
Теперь у нас есть всё что нужно, и мы можем начать процесс оптимизации. Но прежде чем мы перейдём к самому интересному, я приведу полный код программы. Думаю, будет весьма занятно сравнить его с приведённым парой абзацев выше псевдокодом:
Как видите, ничего сложного.
Так как алгоритм имеет вероятностную природу, случай может распорядиться так, что «отжиг» возьмёт, да и застрянет в локальном минимуме. Поэтому стоит сделать несколько запусков и обратить внимание к какому минимальному значению сходятся результаты.
Программа запускалась с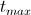 = 10 и
= 10 и 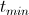 = 0.00001.
= 0.00001.
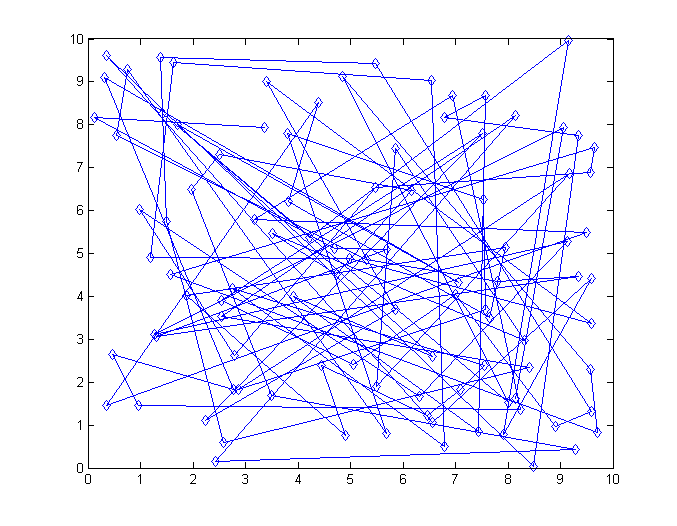
На рисунке изображено состояние на самой первой итерации. Вряд ли коммивояжер испытал бы огромную радость предложи мы ему такой маршрут.
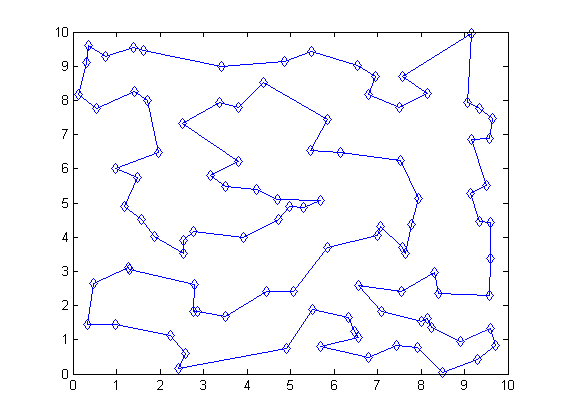
Результат на выходе выглядит куда приятнее:
Однако, стоит отметить, что не смотря на то, что алгоритм в текущей реализации работает достаточно эффективно (точно гораздо быстрее полного перебора), есть мнение, что можно добиться куда лучшего времени без потери «качества». Для этого предлагаю Вам, в качестве практического задания поэкспериментировать с функцией T и поделиться результатами в комментариях.
Исходные коды можно скачать здесь.
Надеюсь, что прочтённое оказалось полезным для вас. Конструктивная критика приветствуется.
P.S.
Пользуясь случаем, хотел бы поблагодарить Антонову Анну и Дмитрия Игнатова, которые прочли статью перед публикацией и дали мне несколько хороших советов.
Для понимания статьи Вам понадобятся минимальные навыки программирования и владение математикой на уровне 9 класса средней школы. Статья рассчитана на людей не знакомых с методами оптимизации или только делающих первые шаги в этом направлении.

Чтобы максимально расширить круг читателей, мне пришлось почти полностью отказаться от формальных определений и сознательно пойти на некоторые не совсем точные упрощения. Надеюсь, что с водой я не выплеснул ребёнка (а если это произошло, то буду рад вашим замечаниям).
Об оптимизации
Для того, чтобы понять, что такое оптимизация, стоит сначала узнать, для чего она нужна. Сразу скажу, что с «задачами оптимизации» в повседневной жизни мы сталкиваемся с завидной регулярностью, не отдавая себе в этом отчёта.
Допустим, мы, получив очередную зарплату, решаем подбить семейный бюджет. Нужно распределить деньги так, чтобы в первую очередь удовлетворить самые важные потребности (еда, плата за электричество, интернет и т.д.), а остаток можно спустить на что-нибудь приоритетом пониже. Купить на все деньги дизайнерский телефон и умереть от голода – не самое лучшее решение, не находите?
Или другой вариант, мы решили отправиться в поход и собираем ранец. Одна проблема – вещей очень много, а ранец у нас не слишком большой (да и сами мы имеем ограниченную грузоподъёмность). Мы хотим взять как можно больше наиболее важных для нас предметов. Если мы идём в горы, прихватить с собой страховочный трос – хорошее решение, взять вместо него любимую PlayStation Vita, а остальное место забить печеньками – наверное, не очень.
Так что же делает оптимизация? Она ищет то самое, хорошее решение. Возможно, не самое лучшее из всех, но точно хорошее.
Теперь чуточку формальнее. Если заглянуть в википедию, можно без труда найти вот такое определение:
Оптимальное (от лат. optimus — наилучшее) решение — решение, которое по тем или иным признакам предпочтительнее других. Следовательно, оптимизация – это способ нахождения оптимального решения.
Теперь, давайте представим, что мы можем измерить насколько хорошее наше решение. Например, в случае «задачи про ранец», каждой вещи присвоим натуральное число (чем больше число, тем важнее вещь). Тогда наша задача приобретает уже более чёткую постановку: мы хотим заполнить ранец такими вещами, суммарный приоритет которых будет максимален, а вес не превысит определенного значения. Т.е. мы ищем максимум некоторой функции, которую принято называть целевой.
Чтобы свести всё к единому знаменателю, снова заглянем в википедию:
Оптимизация (математика) — нахождение экстремума (минимума или максимума) целевой функции в некоторой области.
Теперь, когда мы более-менее определились, с тем, что делает оптимизация, появляется резонный вопрос – «Как?».
Конечно, мы можем особо не заморачиваться и перебрать все-все решения, а затем сравнить их. В случае с ранцем, нам, наверное, даже это удастся проделать. Но теперь давайте представим, что наш ранец – вовсе не ранец, а целый поезд с множеством вагонов, а перевозим мы разные товары в другой город. Задача не изменилась (загрузить как можно больше ценного), а целевой функцией будет суммарная стоимость товаров. Сколько времени уйдёт у нас на полный перебор решений? Думаю, что много.
Можно выбирать решения случайно. Допустим, сто каких-нибудь решений, а затем из них взять самое лучшее. Несомненно, это будет значительно быстрее полного перебора, но кто даст гарантию, что наше итоговое решение будет сколько-нибудь близко к экстремуму?
Не буду томить и скажу, что методов оптимизации существует великое множество. Настолько много, что их принято разбивать на классы, все их я перечислять не буду. Скажу лишь, что «имитация отжига» относится к классу стохастических (от греч. στοχαστικός — «умеющий угадывать») или вероятностных методов. А причём здесь вероятность и как она поможет отыскать решение – чуть ниже.
Имитация отжига
Как и всё гениальное, данный метод подсмотрен у матушки природы. За основу взят процесс кристаллизации вещества, который в свою очередь «приручили» хитрые металлурги, для повышения однородности металла.
Напомню, что у каждого металла есть кристаллическая решетка, если совсем коротко, она описывает геометрическое положение атомов вещества. Совокупность позиций всех атомов будем называть состоянием системы, каждому состоянию соответствует определенный уровень энергии. Цель отжига – привести систему в состояние с наименьшей энергией. Чем ниже уровень энергии, тем «лучше» кристаллическая решетка, т.е. тем меньше у нее дефектов и прочнее металл.
В ходе «отжига» металл сначала нагревают до некоторой температуры, что заставляет атомы кристаллической решетки покинуть свои позиции. Затем начинается медленное и контролируемое охлаждение. Атомы стремятся попасть в состояние с меньшей энергией, однако, с определенной вероятностью они могут перейти и в состояние с большей. Эта вероятность уменьшается вместе с температурой. Переход в худшее состояние, как ни странно, помогает в итоге отыскать состояние с энергией меньшей, чем начальная. Процесс завершается, когда температура падает до заранее заданного значения.
Как видите, в рамках данного процесса происходит минимизация энергии. Меняем энергию на нашу целевую функцию, и voilà! Или нет? Давайте задумаемся, а чем же так хорош столь мудрёный процесс? Почему бы нам, например, всегда не переходить в состояния с меньшей энергией?
Примерно так работает имеющий широкое распространение метод градиентного спуска.
На просторах интернета мне удалось отыскать совершенно чудесную картинку, которая как нельзя лучше иллюстрирует все плюсы алгоритма.

Давайте на минуточку представим себя лыжником, несущемся по крутому склону нашей целевой функции. Задача спуститься в самую нижнюю точку (глобальный минимум). Но, как видите, склон нам попался не совсем ровный, есть на нём низменности, заехав в которые, нам может показаться, что мы уже у подножья. Дабы не остаться в дураках, нам придётся проявить любопытство и вскарабкаться на небольшой холмик, чтобы продолжить спуск.
Чтобы метафора стала окончательно понятна, в примере с лыжником склон – функция измерения энергии вещества (она же целевая функция). А вероятностный переход в состояние с большей энергией – карабканье на холм справа от низменности.
Как видите, такой алгоритм позволяет нам с большой вероятностью избежать «застревания» в локальном минимуме.
Теперь мы готовы перейти к более строгому описанию метода. Введём обозначения:
Пусть S – множество всех состояний (решений) нашей задачи. Например, для задачи о ранце это будет множество всевозможных наборов вещей.
Пусть
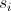 – состояние на i-м шаге алгоритма.
– состояние на i-м шаге алгоритма. 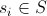 .
. 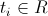 – температура на i-м шаге.
– температура на i-м шаге.Для того, чтобы использовать имитацию отжига, нам понадобится определить три функции:
- Функцию энергии или, проще говоря, то что мы оптимизируем.
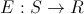
- Функцию изменения температуры с течением времени. На всякий случай оговорюсь, что она обязательно должна быть убывающей.
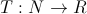
- Функцию, порождающую новое состояние.
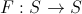
Теперь остановимся на каждой подробнее.
E каждому решению по какому-то правилу ставит в соответствие число. Зависит от конкретной задачи.
T ставит номеру итерации i в соответствие температуру. Функция определяет, как долго будет работать наш алгоритм (на самом деле она имеет более глубокое значение, но нам это знать пока не обязательно). Если T будет линейной функцией, то время работы будет относительно большим. В случае же со степенной функцией, скажем
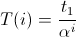 , всё закончится очень быстро, но далеко не факт, что мы не застрянем в низменности, так не добравшись до финиша.
, всё закончится очень быстро, но далеко не факт, что мы не застрянем в низменности, так не добравшись до финиша.Для этой статьи я выбрал самый простой, линейный вариант.
function [ T ] = DecreaseTemperature( initialTemperature, i)
%initialTemperature - начальная температура
%i - номер итерации
T = initialTemperature * 0.1 / i;
end
Сразу оговорюсь, что весь код в этой статье был написан на Matlab. Эту среду я выбрал, так как «из коробки» можно рисовать красивые графики – не более. Писать я старался, не используя специфичной матлабной магии, чтобы код можно было легко портировать на Ваш любимый язык.
Функция F на основе предыдущего состояния порождает новое состояние-кандидат, в которое система может перейти, а может и отбросить. Обозначим его
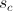 . Способ получения кандидата полностью зависит от решаемой задачи, конкретную функцию Вы сможете увидеть в примере.
. Способ получения кандидата полностью зависит от решаемой задачи, конкретную функцию Вы сможете увидеть в примере.Теперь мы можем в самом общем виде описать алгоритм метода имитации отжига:
- На входе: минимальная температура
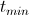 , начальная температура
, начальная температура 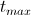
- Задаём произвольное первое состояние
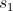
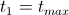
- Пока
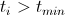
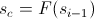
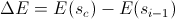
- Если
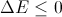 , тогда
, тогда 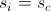
- Если
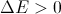 переход осуществляется с вероятностью
переход осуществляется с вероятностью 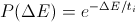
- Понижаем температуру
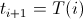
- Возвращаем последнее состояние s
Как видите, всё очень просто, отдельно стоит пояснить только переход в новое состояние. Если энергия «кандидата» меньше, он становится новым состоянием, в противном случае, переход будет вероятностным (поэтому метод относят к классу стохастических).
Чтобы это точно не вызывало трудностей, я позволю себе напомнить некоторые самые базовые понятия теории вероятностей.
Неформально определим вероятность, как меру возможности наступления некоторого события. Вероятность достоверного события (событие, которое точно случится) равна единице, невозможного – нулю. Все остальные значения находятся между.
Например, при броске игральной кости вероятность выпадения любого числа равна единице, а тройки – 1/6.
В нашем случае, подставив в формулу значения разницы энергий
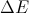 и температуры
и температуры 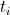 мы получим вероятность перехода. Остаётся только этот переход осуществить, но как это сделать?
мы получим вероятность перехода. Остаётся только этот переход осуществить, но как это сделать? Код вычисления вероятности:
function [ P ] = GetTransitionProbability( dE, T )
P = exp(-dE/T);
end
Давайте представим себе единичный отрезок и разобьём его на две части относительно значения нашей вероятности.

Затем воспользуемся функцией генерации равномерно распределенного случайного числа, в Matlab это rand (как и почти во всех остальных языках). Теперь отметим это число на отрезке.

Если число попало в левую часть – осуществляем переход, в правую – не делаем ничего.
function [ a ] = IsTransition(probability)
value = rand(1);
if(value <= probability)
a = 1;
else
a = 0;
end
end
Теперь, думаю, всё понятно, и мы можем перейти непосредственно к решению нашей первой задачи.
Задача коммивояжёра
Представьте себе, что Вы странствующий торговец и хотите предложить свой товар жителям каждого города в стране. Путешествия отнимают много сил и времени, поэтому логично, что Вы хотите составить свой маршрут таким образом, чтобы расстояние, которое предстоит преодолеть, было минимальным. Этот маршрут и предстоит отыскать.
Более формально: необходимо найти кратчайший путь, проходящий через каждый город и заканчивающийся в точке отправления.
В такой постановке задача называется замкнутой задачей коммивояжёра.
Для начала давайте определимся с данными. Пусть наши города случайным образом разбросаны в квадрате 10x10. Каждый город, соответственно, представлен парой координат. Всего 100 городов.

Данные можно без труда получить в Matlab при помощи следующего кода:
data = rand(2,100)*10;
В других языках придётся написать цикл, но по сути это ничего не меняет. Мы генерируем случайные числа уже знакомой нам функцией rand() и домножаем их на 10, чтобы они лежали в заданной области.
Решение задачи методом имитации отжига
Обозначим множество всех городов C, общее количество обозначается |C| и в нашем случае равно 100. Каждый город
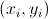 с соответствующим индексом.
с соответствующим индексом. По условию, решением является маршрут между всеми городами, значит множество состояний S – это все возможные маршруты, проходящие через каждый город. Другими словами множество всех упорядоченных последовательностей элементов C, в которой всякий
Как мы помним, для того, чтобы использовать метод имитации отжига мы должны определить две функции, зависящие от каждой конкретной задачи. Это функция энергии E (или «целевая функция» в общепринятой терминологии) и функция F, порождающая новое состояние.
Так как мы стремимся минимизировать расстояние, оно и будет «энергией». Следовательно, наша целевая функция будет иметь такой вид:
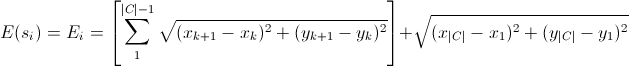
Здесь написано не что иное, как сумма Евклидовых расстояний между парами городов в маршруте
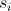 . Так как задача замкнутая, мы были вынуждены подписать
. Так как задача замкнутая, мы были вынуждены подписать 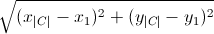 в конце, это расстояние между последним и первым городом. Если не углубляться, то Евклидово – это то самое расстояние между точками, которое мы все проходили на уроках геометрии. Задаётся оно следующей формулой:
в конце, это расстояние между последним и первым городом. Если не углубляться, то Евклидово – это то самое расстояние между точками, которое мы все проходили на уроках геометрии. Задаётся оно следующей формулой:
Где
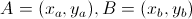
Теперь давайте подумаем, как же нам получать новое состояние? Первое что приходит в голову – менять местами два произвольных города в маршруте. Идея правильная, но такое изменение непредсказуемо влияет на
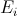 , метод будет работать долго и не факт, что успешно.
, метод будет работать долго и не факт, что успешно.Хорошим вариантом в данном случае будет выбрать два произвольных города в маршруте и инвертировать путь между ними. Например, у нас был маршрут (1,2,3,4,5,6,7). Генератор случайных чисел выбрал города 2 и 7, мы выполнили процедуру и получили (1,7,6,5,4,3,2).
Ниже представлен код для функции F:
function [ seq ] = GenerateStateCandidate(seq)
%seq - предыдущее состояние (маршрут), из которого
%мы хотим получить состояние-кандидат
n = size(seq,1); % определяем размер последовательности
i = randi(n,1); % генерируем целое случайное число
j = randi(n, 1);% генерируем целое случайное число
if(i > j)
seq(j:i) = flipud(seq(j:i)); % обращаем подпоследовательность
else
seq(i:j) = flipud(seq(i:j));% обращаем подпоследовательность
end
end
Теперь у нас есть всё что нужно, и мы можем начать процесс оптимизации. Но прежде чем мы перейдём к самому интересному, я приведу полный код программы. Думаю, будет весьма занятно сравнить его с приведённым парой абзацев выше псевдокодом:
function [ state ] = SimulatedAnnealing( cities, initialTemperature, endTemperature)
n = size(cities,1); % получаем размер вектора городов
state = randperm(n); % задаём начальное состояние, как случайный маршрут
% Функция randperm(n) - генерирует случайныую последовательность из целых чисел от 1 до n
currentEnergy = CalculateEnergy(state, cities); % вычисляем энергию для первого состояния
T = initialTemperature;
for i = 1:100000 %на всякий случай ограничеваем количество итераций
% может быть полезно при тестировании сложных функций изменения температуры T
stateCandidate = GenerateStateCandidate(state); % получаем состояние-кандидат
candidateEnergy = CalculateEnergy(stateCandidate, cities); % вычисляем его энергию
if(candidateEnergy < currentEnergy) % если кандидат обладает меньшей энергией
currentEnergy = candidateEnergy; % то оно становится текущим состоянием
state = stateCandidate;
else
p = GetTransitionProbability(candidateEnergy-currentEnergy, T); % иначе, считаем вероятность
if (MakeTransit(p)) % и смотрим, осуществится ли переход
currentEnergy = candidateEnergy;
state = stateCandidate;
end
end;
T = DecreaseTemperature(initialTemperature, i) ; % уменьшаем температуру
if(T <= endTemperature) % условие выхода
break;
end;
end
end
Как видите, ничего сложного.
Результаты
Так как алгоритм имеет вероятностную природу, случай может распорядиться так, что «отжиг» возьмёт, да и застрянет в локальном минимуме. Поэтому стоит сделать несколько запусков и обратить внимание к какому минимальному значению сходятся результаты.
Программа запускалась с
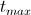 = 10 и
= 10 и 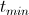 = 0.00001.
= 0.00001.На рисунке изображено состояние на самой первой итерации. Вряд ли коммивояжер испытал бы огромную радость предложи мы ему такой маршрут.
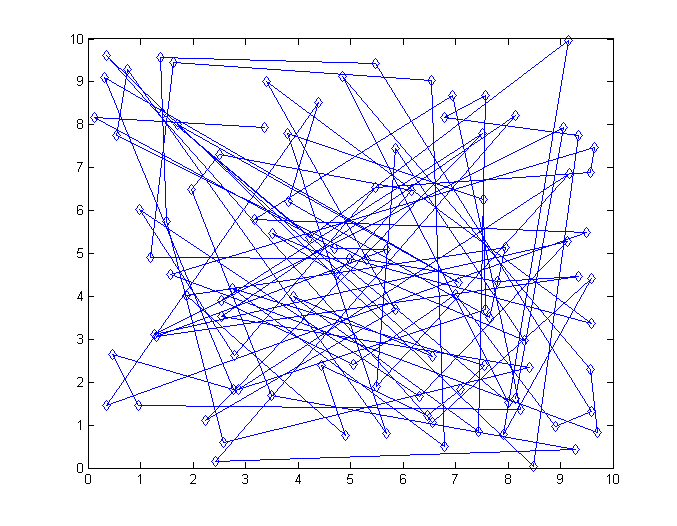
Результат на выходе выглядит куда приятнее:
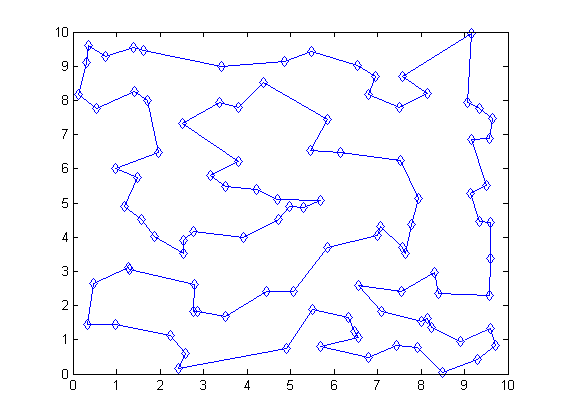
Однако, стоит отметить, что не смотря на то, что алгоритм в текущей реализации работает достаточно эффективно (точно гораздо быстрее полного перебора), есть мнение, что можно добиться куда лучшего времени без потери «качества». Для этого предлагаю Вам, в качестве практического задания поэкспериментировать с функцией T и поделиться результатами в комментариях.
Исходные коды можно скачать здесь.
Надеюсь, что прочтённое оказалось полезным для вас. Конструктивная критика приветствуется.
P.S.
Пользуясь случаем, хотел бы поблагодарить Антонову Анну и Дмитрия Игнатова, которые прочли статью перед публикацией и дали мне несколько хороших советов.