 На Хабре периодически появляются статьи, которые так или иначе относятся к понятию цвета: его общая теория, применение цветовых профилей и систем управления цветом, подбор гармоничных сочетаний цветов в дизайне, описание проблем, которые возникают при работе с изображениями, да и множество других топиков, например, на тему обработки изображений, так или иначе затрагивают вопросы цвета и цветовоспроизведения. Но, к сожалению, большинство таких статей описывают понятие цвета и особенности его воспроизведения очень поверхностно или в них делаются поспешные выводы или даже ошибки. Количество статей и вопросов на профильных форумах об практических аспектах точного цветовоспроизведения, а также множество неверных попыток дать ответы на эти вопросы даже самими опытными специалистами, говорит о том, что проблемы при работе с цветом возникают довольно часто, а найти аргументированные и чёткие ответы на них трудно.
На Хабре периодически появляются статьи, которые так или иначе относятся к понятию цвета: его общая теория, применение цветовых профилей и систем управления цветом, подбор гармоничных сочетаний цветов в дизайне, описание проблем, которые возникают при работе с изображениями, да и множество других топиков, например, на тему обработки изображений, так или иначе затрагивают вопросы цвета и цветовоспроизведения. Но, к сожалению, большинство таких статей описывают понятие цвета и особенности его воспроизведения очень поверхностно или в них делаются поспешные выводы или даже ошибки. Количество статей и вопросов на профильных форумах об практических аспектах точного цветовоспроизведения, а также множество неверных попыток дать ответы на эти вопросы даже самими опытными специалистами, говорит о том, что проблемы при работе с цветом возникают довольно часто, а найти аргументированные и чёткие ответы на них трудно.Недостаточные или ошибочные знания большинства IT специалистов относительно цветовоспроизведения, по моему мнению, объясняются тем, что на изучение теории цвета тратится очень мало времени, так как её основы обманчиво простые: так как на сетчатке глаза есть три вида колбочек, то смешивая определённые три цвета можно без проблем получить всю радугу цветов, что подтверждается регуляторами RGB или CMYK в какой то программе. Большинству этого кажется достаточно, и ихняя тяга к знаниям в этой области заканчивается. Но, процессы получения, создания и воспроизведения изображений готовят Вам множество нюансов и возможных проблем, решить которые поможет понимание теории цвета, а также процессов в основе которых она лежит. Этот топик призван восполнить пробел знаний в области цветоведения, и будет полезен большинству дизайнеров, фотографов, программистов, а также, надеюсь, другим IT специалистам.
Попробуйте дать ответ на следующие вопросы:
- почему физика не может дать определения понятию цвета?
- какая из семи основных единиц измерений СИ основывается на свойствах зрительной системы человека?
- какого цветового тона нет в спектре?
- как удалось измерить ощущение цвета человеком ещё 90 лет назад?
- где используются цвета, которые не имеют яркости?
Если хоть один на вопрос у Вас не нашёлся ответ, рекомендую заглянуть под кат, где Вы сможете найти ответы на все эти вопросы.
Определение понятия цвета. Его измерение
Всем нам известно, что наука не может обойтись без измерений и единиц измерения, и наука про цвет не исключение. Поэтому сначала попытаемся дать определение понятию цвета, и основываясь на этом определении попробуем найти способы его измерения.
Никто не удивится, услышав, что цвета воспринимаются нами при помощи глаз, которые улавливают для этого свет окружающего нас мира. Свет — это электромагнитное излучение диапазона длин волн 390-740 нм (видимого для глаза), поэтому попробуем найти ключ к способам измерения цвета в свойствах этих лучей, предполагая, что цвет — это особенности попавшего нам в глаза света. Это никак не противоречит нашим размышлениям: именно свет попадая в глаза заставляет человека воспринимать цвет.
Физике известны и легко поддаются измерению такие параметры света как мощность и его спектральный состав (то есть распределение мощностей по длинам волн — спектр). Измерив спектр отражённого света, например, от синей и красной поверхности, мы увидим что находимся на правильном пути: графики распределения мощностей будут существенно отличаться, что подтверждает наше предположение, что цвет — это свойство видимого излучения, так как эти поверхности разного цвета. Первая трудность, которая нас подстерегает, это необходимость записывать не меньше 35 числовых значений спектра (видимый диапазон длин волн 390-740 нм с шагом 10 нм) для описания одного цвета. Ещё не успев начать обдумывать способы решения этой второстепенной проблемы, ми обнаружим, что спектры некоторых идентичных по цвету образцов ведут себя странно (красный и зелёный график):

Мы видим, что спектры отличаются существенно, несмотря на безошибочно одинаковый цвет образцов (в данном случае — серого цвета; такие два излучения именуются метамерными). На формировании ощущения цвета этих образцов влияние оказывает только свет, который от них отражён (упустим здесь влияние цвета фона, уровень адаптации глаза к освещению и другие второстепенные факторы), потому его спектральное распределение — это всё что могут нам дать физические измерения наших образцов. В данном случае, два существенно разных распределения спектра определяют один и тот же цвет.
Приведём второй пример проблемы спектрального описания цвета. Мы знаем, что лучи каждого участка видимого спектра окрашены для нас в определённый цвет: от синего в районе 400 нм, через голубой, зелёный, жёлтый, оранжевый к красному с длиной волны 650 нм и выше. Жёлтый находится где то в районе 560-585 нм. Но мы можем подобрать такую смесь красного и зелёного излучений, которая будет восприниматься жёлтой несмотря на полное отсутствие какого либо излучения в «жёлтом» диапазоне 560-585 нм.
Получается, что никакие физические параметры не могут объяснить идентичность цвета в первой и наличие жёлтой окраски лучей во второй ситуации. Странная ситуация? Где мы допустили ошибку?
Проводя эксперимент с измерением спектров, мы предположили что цвет — это свойство излучения, но наши результаты это опровергают, потому что нашлись разные за спектром лучи света, которые воспринимаются как один и тот же цвет. Если бы наше предположение было верным, каждое заметное изменение кривой спектра вызывало бы воспринимаемые изменения цвета, что не наблюдается. Так как сейчас мы ищем способы цветовых измерений, и мы увидели что измерение спектров нельзя назвать измерением цвета, нам нужно искать другие пути, при помощи которых это будет осуществимо.
В действительности, в первом случае было проведено два эксперимента: один с использованием спектрометра, результатом которого были два графика, а другой — визуальное сравнение образцов человеком. Первый способ измеряет спектральный состав света, а второй сопоставляет ощущения в сознании человека. Ввиду того, что первый способ нам не подходит, попробуем задействовать человека для измерения цвета, предположив что цвет — это ощущение, которое испытывает человек при воздействии света на его глаза. Но как измерить ощущения человека, понимая всю сложность и неопределённость этого понятия? Электроды в мозг или энцефалограмму не предлагать, потому что такие методы даже сейчас не дают нужной точности для такого тонкого понятия как цвет. Более того, данная проблема была успешно решена ещё в 20-х годах ХХ века без наличия большинства нынешних технологий.
Яркость
Первая проблема для решения которой стало необходимо численно выразить зрительные ощущения человека, была задача измерения яркости источников света. Измерение мощности излучения ламп (именно мощность излучения, в джоулях, или ваттах, а не потребляемая электрическая мощность) не давало ответа на этот вопрос, потому что, во первых, человек не видит излучения с длинами волн меньше 380 и больше 780 нм, и поэтому любое излучение вне этого диапазона не влияет на яркость источника. Во вторых, как мы уже видели со спектрами, ощущения цвета (и яркости) более сложный процесс чем просто фиксирование характеристик попавшего нам в глаза света: зрение человека более чувствительно к одним зонам спектра, и менее к другим. Например, зелёное излучение намного ярче идентичного по мощности синего. Очевидно, что для решения проблемы численного выражения яркости источников света, нужно количественно определить чувствительность зрительной системы человека для всех отдельных волн спектра, которую потом можно использовать для расчёта вклада каждой длины волны источника в его суммарную яркость. Как и поднятая выше задача с измерением цвета, эта тоже сводится к необходимости измерения ощущения яркости человеком.
Измерить ощущение яркости от излучений каждой длины волны удалось путём визуального сравнения человеком яркостей излучений с известными мощностями. Это довольно просто: управляя интенсивностью излучения, нужно уравнять яркости двух монохроматических (спектрально максимально узких) потоков, измерив при этом их мощности. Например, чтобы уравнять по яркости монохроматическое излучение с длиной волны 555 нм мощностью один ватт нужно использовать двухватное излучения с длиной волны 512 нм. То есть, наша зрительная система вдвое чувствительнее к первому излучению. На практике, для высокой точности результатов был проведён более сложный эксперимент, но это не меняет сути сказанного (детально процесс описан в оригинальном научном труде 1923 года). Результатом серии таких экспериментов для всего видимого диапазона является кривая спектральной световой эффективности (ещё можно встретить название «кривая видности»):
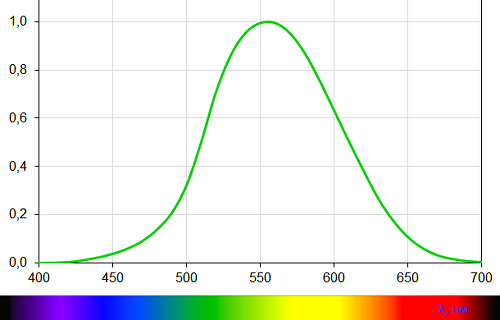
по оси Х отложены длины волн, по оси Y — относительная чувствительность зрительной системы человека к соответствующей длине волны.
Имея прибор с такой же спектральной чувствительностью, можно с лёгкостью определять на нём яркость нужных световых излучений. Именно под такую кривую тщательно подстраивается чувствительность различных фотометров, люксметров и других приборов, в работе которых важно определение воспринимаемой человеком яркости. Но чувствительность таких приборов всегда является только приближением к кривой спектральной световой эффективности человека и для более точных измерений яркости используют спектральное распределение интересующего источника света.
Спектральное распределение получают разделением излучения на узкие спектральные зоны и измерением мощности каждой из них отдельно. Мы можем рассматривать яркость нашего источника как сумму яркости всех этих спектральных зон, и для этого определим яркость каждого из них (формула для тех, кому не интересно читать мои объяснения на пальцах): умножаем измеренную мощность на соответствующую этой длине волны чувствительность нашей зрительной системы (оси Y и X предыдущего графика соответственно). Просуммировав полученные таким образом яркости всех зон спектра, мы получим яркость нашего первичного излучения в фотометрических единицах, которые дают точное представление об воспринимаемой яркости тех или иных объектов. Одна из фотометрических единиц входит в Основные единицы СИ — кандела, которая определяется через кривую спектральной световой эффективности, то есть основывается на свойствах зрительной системы человека. Кривая относительной чувствительности зрительной системы человека была принята в качестве международного стандарта в 1924 году Международной комиссией по освещению (в советской литературе можно встретить сокращение МКО), или CIE — Commission Internationale de l'Éclairage.
Система CIE RGB
Но, кривая спектральной световой эффективности даёт нам представление только об яркости светового излучения, а мы можем назвать другие его характеристики, например, насыщенность и цветовой тон, которые при её помощи нельзя выразить. По способу измерения яркости, ми теперь знаем, что «измерять» цвет может только непосредственно человек (не забываем, что цвет — это ощущение) или некая модель его реакции, такая как кривая спектральной световой эффективности, которая позволяет численно выразить ощущения яркости. Предположим, что для измерения цвета, нужно экспериментально при помощи человека создать, по аналогии с кривой световой эффективности, некую систему, которая будет отображать цветовую реакцию зрительной системы на все возможные варианты спектрального распределения света.
Уже давно известно одно свойство лучей света (на самом деле, это особенность нашей зрительной системы): если смешать два разноцветных излучения, можно получить цвет, который будет совсем не похож на изначальные. Например, направив на белый лист бумаги в одну точку зелёный и красный свет определённых мощностей, можно получить чисто жёлтое пятно без примесей зелёных или красных оттенков. Добавив третье излучение, а к имеющимся двум лучше подойдёт синее (потому что его никак не получить смесью красного и зелёного), мы получим систему, которая позволит нам получать множество цветов.
Если визуально уравнять в таком приборе некое тестовое излучение, мы получим три показателя: интенсивность красного, зелёного и синего излучателей соответственно (как приложенное к лампам напряжение, например). То есть, при помощью нашего прибора (именуемого визуальным колориметром), который воспроизводит цвет, и нашей зрительной системы, нам удалось получить численные значения цвета некого излучения, к чему мы и стремились. Такие три значения часто именуют координатами цвета, потому что их удобно представить как координаты трёхмерного пространства.
Подобные эксперименты успешно провели в 20-х годах ХХ века независимо друг от друга учёные Джон Гилд (John Guild) и Дэвид Райт (David Wright). В качестве основных излучений у Райта использовались монохроматические излучения красного, зелёного и синего цветов с длинами волн 650, 530 и 460 нм соответственно, а Гилд использовал более сложные (не монохроматические) излучения. Несмотря на существенные отличия в используемом оборудовании и на то, что данные были усреднены только по 17-ти наблюдателям с нормальным зрением (10 у Райта и 7 у Гилда) итоговые результаты обоих исследователей оказались очень близки друг к другу, что говорит об высокой точности измерений, проведённых учёными. Схематически, процедура измерений изображена на рисунке:
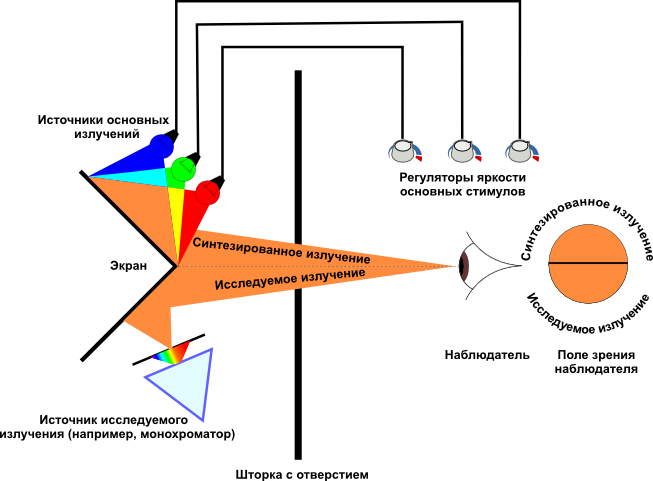
На верхнюю часть экрана проецируется смесь излучений от трёх источников, а на нижнюю — изучаемое излучение, а участник опыта видит их одновременно через отверстие в шторке. Исследователь ставит перед участником задачу уравнять цвет между полями прибора, и направляет при этом исследуемое излучение на нижнее поле. Участник регулирует мощности трёх излучений пока ему это не удастся, а исследователь записывает показатели интенсивности трёх источников.
В ряде случаев, не удаётся уравнять определённые монохроматические излучения при таком эксперименте: тестовое поле при любом положении регуляторов трёх излучений остаётся более насыщенным чем используемая смесь. Но, в силу того, что целью эксперимента является получение координат цвета, а не его воспроизведение, исследователи пошли на хитрость: одно основное излучение прибора они смешали не с двумя другими, а направили его на нижнюю часть экрана, то есть смешали его с тестовым излучением:
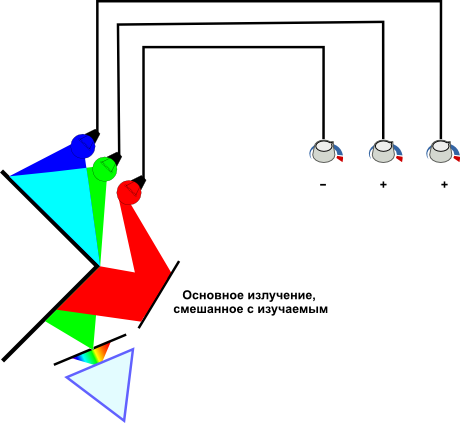
Далее уравнивание проводится как обычно, но количество того излучение, которое смешано с изучаемым, будет считаться отрицательным. Здесь можно провести аналогию со сменой знака при переносе числа в другую часть обычного уравнения: так как между двумя частями экрана колориметра установлено визуальное равенство, верхнюю его часть можно рассматривать как одну часть уравнения, а нижнюю — как другую.
Оба исследователя провели визуальные измерения всех отдельных монохроматических излучений видимого спектра. Изучая таким способом свойства видимого спектра, учёные предполагали, что их результаты можно будет использовать для описания любых других излучений. Учёные оперировали мощностями трёх независимых излучений и результатом серии таких экспериментов являются три кривые, а не одна как это было сделано при создании кривой световой эффективности.
Для создания удобной и универсальной системы спецификации цвета комитет CIE провели усреднения данных измерений Гилда и Райта пересчитав их данные для тройки основных излучений с длинами волн 700, 546,1 и 435,8 нм (красное, зелёное и синее, red, green, blue — RGB). Зная соотношение яркостей основных излучений такой усреднённой системы, которые нужны для воспроизведения белого цвета (соответственно 1:4.5907:0.0601 для красного, зелёного и синего лучей, что установлено экспериментально с последующим пересчётом) и используя кривую спектральной эффективности, члены CIE рассчитали кривые удельных координат цвета, которые показывают нужное количество трёх основных излучений этой системы для уравнения любого монохроматического излучения мощностью один ватт:

по оси Х отложены длины волн, а по оси Y — нужные количества трёх излучений необходимые для воспроизведения цвета, вызываемого соответствующей длиной волны. Негативные участки графиков соответствуют тем монохроматическим излучениям, которые не могут быть воспроизведены тремя используемыми в системе основными излучениями, и для их спецификации нужно прибегать к описанному выше ухищрению при уравнивании.
Для построения подобной системы можно выбрать любые другие три излучения (при этом помня, что никакое из них не должно воспроизводится смесью двух других), которые дадут нам другие удельные кривые. Выбранные в системе CIE RGB основные излучения воспроизводят большое число излучений спектра, а её удельные кривые получены с большой точностью и стандартизированы.
Кривые удельных координат цвета избавляют от необходимости использовать громоздкий визуальный колориметр, с его медленным методом визуального уравнивания для получения координат цвета при помощи человека, и позволяют рассчитывать их только по спектральному распределение излучения, получить которые довольно быстро и просто при помощи спектрометра. Такой метод возможен, потому что любое излучение можно представить как смесь монохроматических лучей, мощности которых отвечают интенсивности соответствующей зоны спектра этого излучения.
Теперь проверим наши два образца, перед которыми сдалась физика, показывая разные спектры для одноцветных объектов, используя кривые удельных координат формула: поочерёдно умножим спектральное распределение мощностей отражённого от образцов света на три удельные кривые и просуммируем результаты для каждой из них (как при расчёте яркости из спектрального распределения, но здесь используются три кривые). Результатом будет три числа, R, G и B, которые являют собой координаты цвета в системе CIE RGB, то есть количества трёх излучений этой системы, смесь которых идентична по цвету с измеряемым. Мы получим три одинаковые показатели RGB для двух наших образцов, что соответствует нашему идентичному ощущению цвета и подтверждает наше предположение что цвет — это ощущение и измерять его можно только при участии нашей зрительной системы, или её модели в виде трёх кривых системы CIE RGB или какой либо другой, удельные координаты которой известны (другую такую систему, базирующейся на других основных цветах, мы рассмотрим детально чуть позже). Используя колориметр CIE RGB для измерения отражённого от образцов света непосредственно, то есть визуально уравнивая цвет смеси трёх излучений системы с цветом каждого образца, мы получим те же три координаты RGB.
Нужно отметить, что в колориметрических системах принято нормировать количества основных излучений так, чтобы R=G=B=1 соответствовало принятому в системе белому цвету. Для системы CIE RGB таким белым цветом принят цвет гипотетического равноэнергетического источника, который излучает равномерно на всех длинах волн видимого спектра. Без такой нормировки, система получается неудобной, потому что яркость синего источника очень мала — 4.5907:0.0601 против зелёного, и на графиках большинство цветов «прилипало» бы к синей оси диаграммы. Введя такую нормировку (соответственно 1:4.5907:0.0601 для красного, зелёного и синего лучей системы) ми перейдём от фотометрических к колориметрическим единицам что сделает такую систему более удобной.
Следует обратить внимание, что система CIE RGB не базируется на какой либо теории цветового зрения, а кривые удельных координат цвета не являются спектральной чувствительностью трёх видов колбочек сетчатки глаза человека, как они часто ошибочно интерпретируются. Такая система легко обходится без данных про свойства пигментов колбочек сетчатки и без каких либо данных про сложнейшие процессы обработки зрительной информации в нашем мозгу. Это говорит об исключительной изобретательности и дальновидности учёных, которые создали такую систему несмотря на ничтожные сведения про свойства зрительного аппарата человека на то время. Более того, система CIE RGB лежит в основе науки о цвете практически без изменений до сих пор, несмотря на колоссальный прогресс науки за прошедшее время.
Также нужно отметить, что несмотря на то, что монитор для воспроизведения цвета также использует три излучения как и система СIE RGB, три значения цветовых компонент монитора (RGB) не будут строго специфицировать цвет, потому что разные мониторы воспроизводят цвет по разному с довольно большим разбросом, и к тому же, основные излучения мониторов довольно сильно отличаются от основных излучений системы СIE RGB. То есть, не следует воспринимать RGB значения монитора как некий абсолют определения цвета.
Для лучшего понимания, необходимо отметить, что говоря «излучение/источник/длина волны/лампа имеет зелёный цвет» мы на самом деле имеем ввиду что «излучение/источник/длина волны/лампа вызывает ощущение зелёного цвета». Излучение видимого диапазона — это только стимул для нашей зрительной системы, а цвет — это результат восприятия этого стимула и не следует приписывать цветовые свойства электромагнитным волнам. Например, как в примере выше, никакие волны с жёлтого диапазона спектра не появляются при смешении красных и зелёных монохроматических лучей, но их смесь мы воспринимаем жёлтой.
Нереальные цвета. Система CIE XYZ
В 1931 году в Тринити-колледже Кембриджского университета (Великобритания) на очередном заседании CIE система основанная на данных Гилда и Райта была принята в качестве международного стандарта. Также, группа учёных, во главе с американцем Дином Джаддом (Deane B. Judd), чтобы не ждать очередного заседания комитета, которое произойдёт не раньше чем через год, предложила другую систему спецификации цвета, окончательные данные которой были рассчитаны только в ночь перед заседанием. Предложенная система оказалась настолько удобной и удачной, что она была принята комитетом без каких либо серьёзных обсуждений.
Чтобы понять на основе чего была создана такая система, цвет нужно представить в виде вектора, потому что сложение двух и более цветов подчиняется тем самим правилам что и сложение векторов (это выплывает из законов Грассмана). Например, результат смешивания излучения красного цвета с зелёным можно представить как сложение двух векторов с длинами, которые пропорциональны яркости этих излучений:
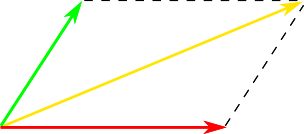
Яркость смеси будет равна длине полученного сложением вектора, а цвет будет зависеть от соотношения яркости используемых излучений. Чем соотношение больше в пользу одного из первичных цветов, тем больше результирующее излучение будет ближе по цвету к этому излучению:

Попробуем подобным образом графически изобразить смешение цветов в используемом для создания системы CIE RGB колориметре. Как помним, в нём используются три излучения красного, зелёного и синего цвета. Никакой цвет этой тройки не получить суммой двух остальных, поэтому представлять все возможные смеси этих излучений нужно будет в трёхмерном пространстве, что не мешает нам использовать векторные свойства сложения цветов при этом:

Не всегда удобно чертить трёхмерные диаграммы, поэтому часто используют упрощённый график, который являет собой проекцию всех нужных цветов на единичную плоскость (выделена синим) трёхмерной схемы:

Результатом такой проекции вектора цвета будет точка на диаграмме, осями которой будут стороны треугольника, которые задаются точками основных цветов системы СIE RGB:

Такая точка будет иметь координаты в системе этого треугольника в виде расстояние от любых двух его сторон (третья координата лишняя, так как в треугольнике любую точку можно определить по двум расстояниям от вершин или сторон). Координаты в таком треугольнике называют координатами цветности, и они определяют такие параметры цвета как цветовой тон (синий, голубой, зелёный и т.д.) и насыщенность (серый, бледный, насыщенный и т.п.). В силу того, что мы перешли от трёхмерной к плоской диаграмме, она не позволяет показать третий параметр цвета — яркость, но для многих случаев определение только значения цветности будет достаточно.
Чтобы не путаться, отдельно выделим что координаты цвета — это положение конца вектора цвета в трёхмерной системе, и обозначаются они заглавными буквами (RGB, XYZ, например), а координаты цветности — это положение точки цвета на плоской диаграмме цветностей, и обозначаются они строчными буквами (rg, xy) и их достаточно двух.
Использование координатной системы в которой между осями нет прямого угла не всегда неудобно, поэтому в колориметрии чаще используют такую систему из трёх векторов, единичная плоскость которой формирует прямоугольный треугольник. Две его стороны возле прямого угла используют как оси диаграммы цветности:

Поместим теперь на такую диаграмму все возможные цветности, пределом которых будет линия спектрально чистых излучений с линией пурпурных цветностей, часто именуемая локусом, которая ограничивает на диаграмме область реальных цветов (красная линия):
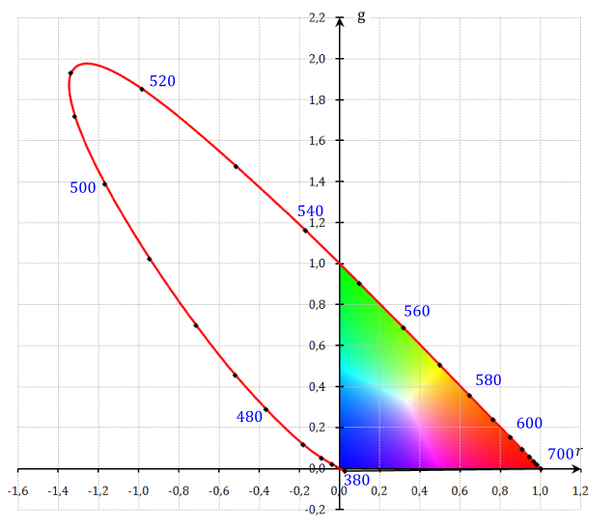
Линия пурпурных цветностей лежит между цветностями излучений крайнего синего и красного концов спектра. Пурпурным цветам мы не можем сопоставить никакую зону спектра, как это можно сделать с любым другим цветом, потому что ощущения пурпурного цвета возникает при одновременном действии на нашу зрительную систему синих и красных лучей, а не какого то одного.
Значительная часть локуса (в зоне 380-546 нм) выходит за пределы треугольника, ограниченного цветностями основных излучений, то есть имеет отрицательные координаты цветности, потому что эту часть спектральных излучений не удалось уравнять на колориметре CIE. Это соответствует кривым удельных координат цвета, в которых тот самый участок спектра имеет отрицательные координаты (в диапазоне 380-440 нм это невидимые на графике малые значения).
Присутствие отрицательных координат цвета и цветности превращало колориметрические расчёты в непростую задачу: в 20-30-х годах большинство расчётов проводились при помощи логарифмической линейки, а объем вычислений в колориметрических работах немаленький.
Предыдущая диаграмма показывает нам, что все положительные координаты имеют только цвета, что лежат в пределах треугольника, который формируют цветности используемых в данной системе основных излучений. Если бы локус лежал в середине треугольника, все цвета имели бы положительные координаты, что бы значительно упростило расчёты. Но найти такие три точки на локусе, которые смогли бы включить его в себя полностью невозможно, в силу его выпуклой формы. Позже было установлено, что причина такой формы локуса кроется в особенностях спектральной чувствительности трёх видов колбочек нашего глаза, которые перекрываются между собой и любое излучение возбуждает колбочки, которые отвечают за другую зону спектра, что понижает уровень насыщенности цвета.
А что если выйти за рамки локуса, и использовать цвета, которые невозможно воспроизвести и увидеть, но координаты которых можно с лёгкостью использовать в уравнениях наравне с координатами реальных цветов? Раз мы уже перешли от экспериментов к расчётам, ничто не мешает нам использовать такие нереальные цвета, потому что все свойства смешения цветов сохраняются при этом! Нам подойдут любые три цвета, чей треугольник сможет включить локус реальных цветов, и мы без трудностей сможем начертить множество таких троек нереальных основных цветов (будет целесообразно строить такой треугольник как можно плотнее вокруг локуса, так будет меньше ненужных областей на диаграмме):
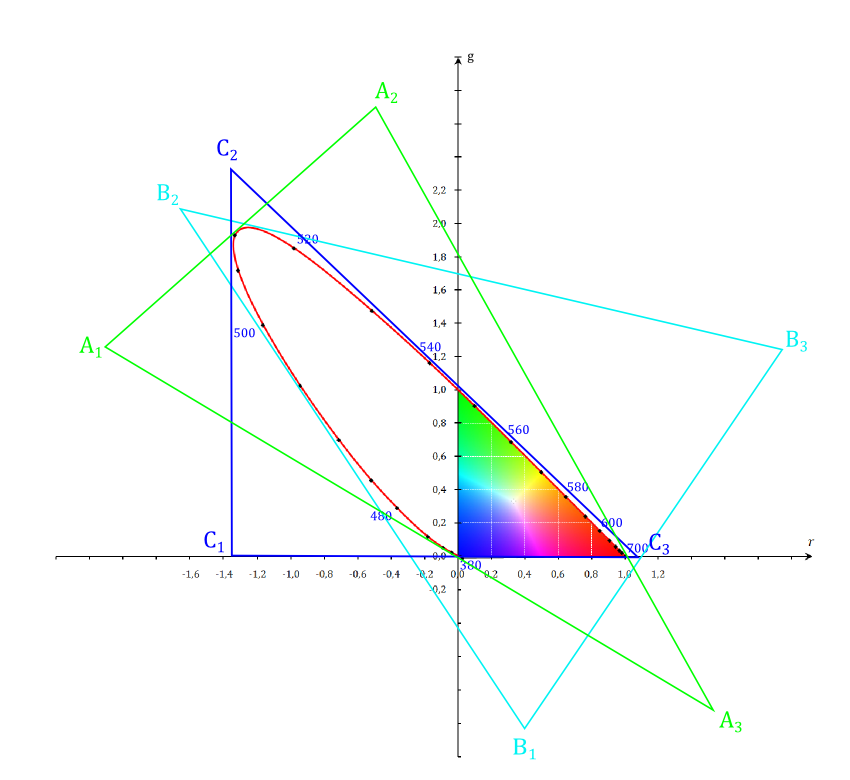
Имея такую свободу в выборе точек новых основных цветов, учёные решили извлечь из этого некоторые полезные возможности для новой трёхцветной системы. Например, возможность определять фотометрическую яркость непосредственно при помощи создаваемой системы без дополнительных расчётов или измерений (в системе CIE RGB яркость нужно рассчитывать), то есть объединить её каким то образом с фотометрическим стандартом 1924 года.
Для обоснования выбора тройки новых цветов (помним, что они существуют только в расчётах), которые были в итоге для этого выбраны учёными, вернёмся на нашу объёмную диаграмму координат цвета. Для наглядности и лёгкости понимания мы будем использовать обычную прямоугольную систему координат. Поместим на неё плоскость, на которой все цвета будут иметь одинаковую фотометрическую яркость. Как помним, единичные яркости красного, зелёного и синего основных излучений в системе СIE RGB соотносятся как 1:4.5907:0.0601, и чтобы перейти обратно к фотометрическим единицам их нужно взять в пропорции 1/1 к 1/4,59 к 1/0,0601, то есть, 1:0,22:17 что даст нам плоскость цветов с одинаковой фотометрической яркостью в колориметрической системе СIE RGB (точка пересечения плоскости с осью B находится за пределами рисунка в позиции 17):

Все цвета, координаты которых находятся на этой плоскости будут, иметь одинаковую фотометрическую яркость. Если провести параллельную плоскость вдвое ниже предыдущей (0,5:0,11:8,5), мы получим место положение цветов с вдвое меньшей яркостью:
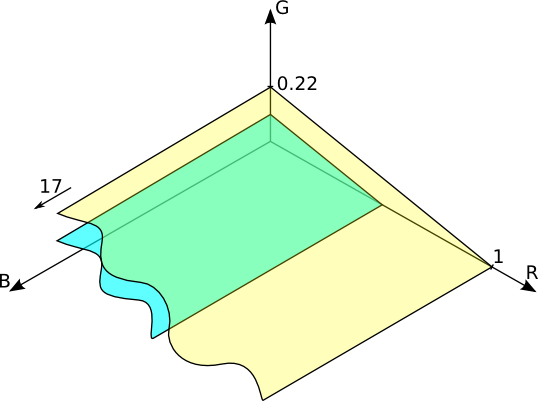
Аналогично, ниже можно провести новую параллельную плоскость, которая пересечёт начало координат, на которой разместятся все цвета с нулевой яркостью, а ещё ниже можно начертить даже плоскости отрицательных яркостей. Это может показаться абсурдным, но вспомним, что работаем с математическим представлением трёхцветной системы, где в уравнениях всё это возможно, чем мы и воспользуемся.
Перейдём обратно на плоскую диаграмму rg, спроектировав на неё плоскость нулевых яркостей. Проекцией будет линия нулевой яркости — алихна, которая пересекает начало координат:
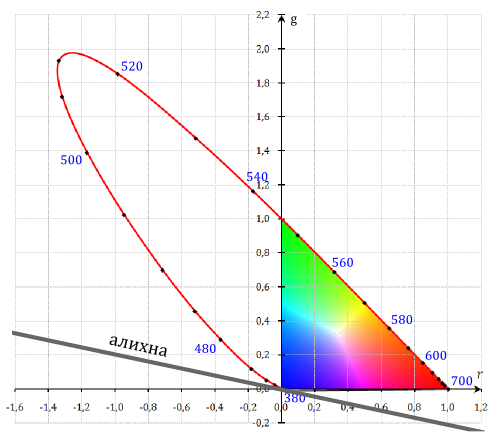
На алихне лежат цветности, которые не имеют яркости, и если использовать размещённый на ней цвет в цветовом уравнивании (не реальным, со смешиванием световых потоков, а в уравнениях, где такие цвета возможны), он не будет влиять на яркость полученной смеси. Если разместить на алихне два цвета трёхцветной системы, то яркость всей смеси будем определятся только одним оставшимся цветом.
Напомню, что мы ищем цветовые координаты таких трёх гипотетических цветов, которые смогут уравнять цвета всех реальных излучений без использования отрицательных значений (треугольник должен включать в себя весь локус) и при этом, новая система будет включать в себя фотометрический стандарт яркости непосредственно. Разместив два цвета на алихне (названные X и Z), а третий выше локуса (Y), мы решим обе проблемы:
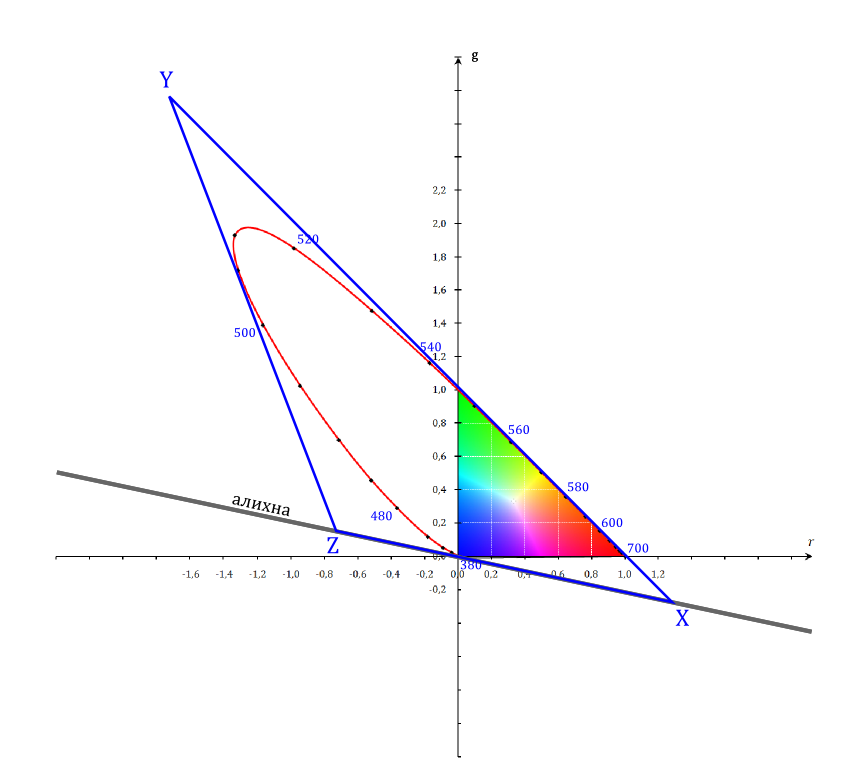
Локус реальных цветов находится полностью в треугольнике, который ограничен тремя выбранными цветами, а яркость полностью перешла к одному из трёх компонент системы — Y. В зависимости от нормировки величин и характера измерений, координата Y может выражать яркость непосредственно в канделах на м2, процент от максимальной яркости какой то системы (дисплея, например), процент пропускания (прозрачные образцы, слайды например) или яркость относительно некоторого эталона (при измерениях отражающих образцов).
Преобразовав полученный треугольник в прямоугольный, ми получим знакомую многим диаграмму цветности xy:

Нужно помнить, что диаграмма xy — это проекция системы с основными точками XYZ на единичную плоскость, аналогично так диаграмма rg и система RGB. Данная диаграмма позволяет в удобной форме иллюстрировать цветности различных излучений, например, цветовые охваты различных устройств. Диаграмма обладает одним полезным свойством: координаты цветности смеси двух излучений будут находится строго на линии, которая соединяет точки этих двух излучений на диаграмме. Поэтому, цветовой охват монитора, например, на такой диаграмме будет являть собой треугольник.
Диаграмма xy имеет также один недостаток, который следует помнить: равные отрезки на разных участках диаграммы не означают одинаковую воспринимаемую разницу в цвете. Это проиллюстрировано двумя белыми отрезками на предыдущем рисунке. Длины этих отрезков соответствуют ощущению одинаковой разницы цветности, но при этом отрезки различаются по длине в три раза.
Рассчитаем кривые удельных координат цвета полученной системы, которые показывают нужное количество трёх основных цветов XYZ для уравнения любого монохроматического излучения мощностью один ватт:

Видим, что в кривых отсутствуют отрицательные участки (что наблюдалось в системе RGB), что и было одной из целей создания системы XYZ. Также, кривая y (игрек с чёрточкой сверху) полностью совпадает с кривой спектральной световой эффективности зрения человека (про неё говорилось выше при объяснении определения яркости световых излучений), поэтому величина Y определяет яркость цвета непосредственно — она рассчитывается идентичным образом как и фотометрическая яркость по той же кривой. Это достигнуто путём размещения двух других цветов системы на плоскости нулевых яркостей. Поэтому, колориметрический стандарт 1931 года включает в себя фотометрический стандарт 1924 года, что позволяет обойтись без лишних расчётов или измерений.
Эти три кривые определяют Стандартного колориметрического наблюдателя — стандарт, который используют при колориметрической интерпретации спектральных измерений и он лежит в основе всей науке о цвете практически без изменений до сих пор. Хотя визуальный колориметр XYZ не может существовать физически, его свойства позволяют с высокой точностью проводить цветовые измерения и он помогает многим отраслям предсказуемо воспроизводить и передавать информацию о цвете. На системе XYZ базируется всё дальнейшие достижения науке о цвете, например знакомая многим система CIE L*a*b* и ей подобные, а также новейшие системы CIECAM, которые используют современные программы построения цветовых профилей.
Итоги
- Точная работа с цветом требует его измерения, которое также необходимо как и измерение длины или веса.
- Измерение воспринимаемой яркости (одного из атрибутов зрительного ощущения) световых излучений невозможно без учёта особенностей нашей зрительной системы, которые были успешно исследованы и заложены во все фотометрические величины (кандела, люмен, люкс) в виде кривой её спектральной чувствительности.
- Простое измерение спектра исследуемого света само по себе не даёт ответа на вопрос о его цвете, потому что легко можно найти разные спектры которые воспринимаются как один цвет. Разные величины, которые выражают один и тот же параметр (цвет, в нашем случае), говорят о несостоятельности такого метода определения.
- Цвет — это результат восприятия света (цветового стимула) в нашем сознании, а не физическое свойство этого излучения, поэтому измерять каким то образом нужно это ощущение. Но прямое измерение ощущений человека невозможно (или было невозможным на момент создания описанных здесь колориметрических систем).
- Эту проблему обошли путём визуального (при участии человека) уравнивания цвета исследуемого излучения при помощи смешения трёх излучений, количества которых в смеси и будут искомым численным выражением цвета. Одной из систем таких трёх излучений есть CIE RGB.
- Экспериментально уравняв при помощи такой системы все монохроматические излучения по отдельности, получают (после некоторых расчётов) удельные координаты этой системы, которые показывают нужные количества её излучений для уравнения цвета любого монохроматического излучения мощностью один ватт.
- Зная удельные координаты, можно рассчитать координаты цвета исследуемого излучения по его спектральному составу без визуального уравнивания цвета человеком.
- Система CIE XYZ создана путём математических трансформаций системы CIE RGB и базируется на тех же принципах — любой цвет можно точно специфицировать количеством трёх излучений, смесь которых воспринимается человеком идентичной по цвету. Основное отличие системы XYZ — цвет её основных «излучений» существует только в колориметрических уравнениях, и получить их физически невозможно.
- Основная причина создания системы XYZ — облегчения расчётов. Координаты цвета и цветности всех возможных световых излучений будут положительными. Также, координата цвета Y выражает фотометрическую яркость стимула непосредственно.
Заключение
Наиболее близкими для ИТ специалистов сферами деятельности, в фундаменте которых лежат описанные в этой статье принципы и системы, является обработка изображений и их воспроизведение различными способами: от фотографии к веб-дизайну и полиграфии. Системы управления цветом непосредственно используют в своей работе колориметрические системы и результаты цветовых измерений, что позволяет предсказуемо воспроизводить цвет различными способами. Но эта тема уже выходит за пределы данной статьи, потому что здесь затронуты основополагающие аспекты теории цвета, а не цветовоспроизведения.
Этот топик не претендует дать исчерпывающие и полные сведения про поднятую тему, а является лишь «картинкой для привлечения внимания» для IT специалистов, многие из которых просто обязаны понимать основы цветоведения. Для облегчения понимания многое здесь упрощено или изложено вскользь, поэтому, привожу список источников, которые будут интересны тем, кто хочет более детально ознакомится с теорией цвета (все книги можно найти в сети):
- Джадд Д., Вышецки Г. Цвет в науке и технике. — «Мир», 1978. Книга одного из авторов системы XYZ. В оригинале — «Color in business, science, and industry»
- Гуревич М.М. Цвет и его измерение. — Издательство Академии наук СССР, 1950. Детально изложены основы науки о цвете; объяснено много нюансов, которые другие источники упускают
- Noboru Ohta, Alan Robertson. Colorimetry: Fundamentals and Applications. — Wiley, 2005.
- R. W. G. Hunt, M. R. Pointer. Measuring Colour, 4th Edition. — Wiley, 2011.