В этой моей статье, как и в предыдущей рассматривается цифровая схемотехника с точки зрения программиста. Но в этот раз будет разобрана «более алгоритмическая» задача сортировки чисел, с разбором verilog-кода. Рассматриваемое аппаратное решение позволяет отсортировать n чисел за время 2*n. На картинке ДПВ показан вывод на монитор от тестового проекта для ПЛИС, там каждой линии соответствует один тик сортировщика, сначала n тиков случайные числа записываются в сортировщик, затем n тиков выводятся числа отсортированные.

Известно, что программная сортировка n чисел в общем случае требует время O(n*log(n)). Аппаратная же позволяет обойти это ограничение, за счёт выполнения нескольких сравнений сразу, см. например сети сортировки. Сеть сортировки работает целиком параллельно, данные приходят и уходят вместе, мой же модуль принимает или выдаёт только одно число за раз, но не требует дополнительного времени: Сначала в буфер записывается N < Nmax чисел за N тактов, затем N тактов оттуда читается (забирается) отсортированная последовательность.
UPDATE: в комментариях меня убедили, что это не даёт права говорить о сложности алгоритма o(n). Если N>Nmax, то сортировать придётся по частям, используя затем сортировку слиянием, затраченное время будет ~N*log(N/Nmax). При N -> inf это даст те же O(n*log(n)). Это, однако не отменяет того факта, что аппаратная сортировка работает быстрее программной.
Посмотрим на исходники на verilog-е. Напомню главное отличие HDL от языка программирования — язык программирования это инструкция для исполнителя, которая исполняется последовательно, строчка за строчкой, а программа на HDL соответствует электронной схеме, все части которой работают одновременно.
Но я сделал ещё одну реализацию с таким же интерфейсом, но немного другими свойствами. Различия реализаций: Первая на основе цепочки сортирующих ячеек, вторая на основе двоичного дерева, в узлах которого такие же ячейки.
Первая реализация позволяет дописывать данные в частично опустошённый буфер (можно, например, сортировать запросы на прерывания по приоритету), древовидная после записи требует полного прочтения.
Преимущество древовидной реализации — в процессе работы двигается не вся цепочка, а только одна ветка — теоретически более энергоэффективно.
Вообще-то, рекурсивные определения модулей это очень нехарактерный стиль для верилога. Должен признаться, данный проект — «паровоз для машиниста». Правильный подход таков, — задана цель написать сортировщик, мы выбираем реализацию — дерево. В моём же случае, сама идея написать сортировщик возникла из необходимости освоить работу с древовидными структурами, — для нужд вычислителя на базе комбинаторной логики. Я уже немного написал об этом проекте в конце своего предыдущего, первого на Хабре поста. Работа машины сводится к вычислению комбинаторного выражения методом параллельного переписывания термов. Основная идея — сопоставить дереву функциональной программы аппаратное дерево ячеек, способных применять комбинаторы. Теоретически, так можно эффективно решать задачи из булевой алгебры или исчисления предикатов, для целей символьных вычислений или доказательства теорем. Надеюсь, в ближайшие месяцы у меня будет готова работающая версия, способная редуцировать простенькие выражения. Если вам известны какие-нибудь практические задачи, хорошо ложащиеся на чистое лямбда исчисление или комбинаторную логику, напишите, пожалуйста, в комментариях.
Исходники модулей сортировщиков здесь под LGPL, есть тестовые проекты для плат Марсоход2, Terasic DE0 и DE2-115.
p.s. прошу прощения за пересоздание топика. Теперь я знаю, что нельзя убирать свежеопубликованный топик в черновики надолго в первые сутки.

Известно, что программная сортировка n чисел в общем случае требует время O(n*log(n)). Аппаратная же позволяет обойти это ограничение, за счёт выполнения нескольких сравнений сразу, см. например сети сортировки. Сеть сортировки работает целиком параллельно, данные приходят и уходят вместе, мой же модуль принимает или выдаёт только одно число за раз, но не требует дополнительного времени: Сначала в буфер записывается N < Nmax чисел за N тактов, затем N тактов оттуда читается (забирается) отсортированная последовательность.
UPDATE: в комментариях меня убедили, что это не даёт права говорить о сложности алгоритма o(n). Если N>Nmax, то сортировать придётся по частям, используя затем сортировку слиянием, затраченное время будет ~N*log(N/Nmax). При N -> inf это даст те же O(n*log(n)). Это, однако не отменяет того факта, что аппаратная сортировка работает быстрее программной.
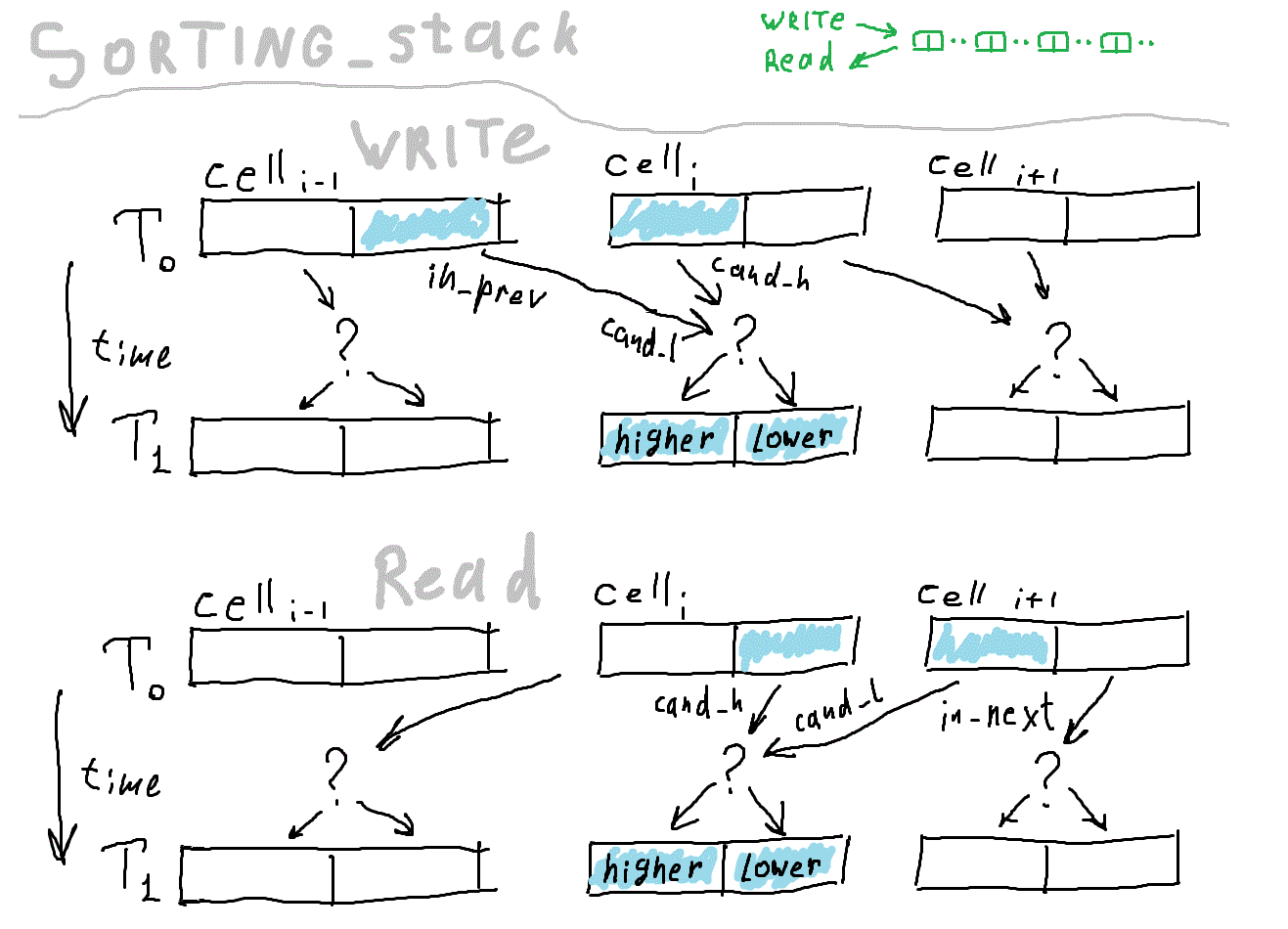
На картинке дано условное описание основной версии алгоритма. Надеюсь, смысл можно уловить.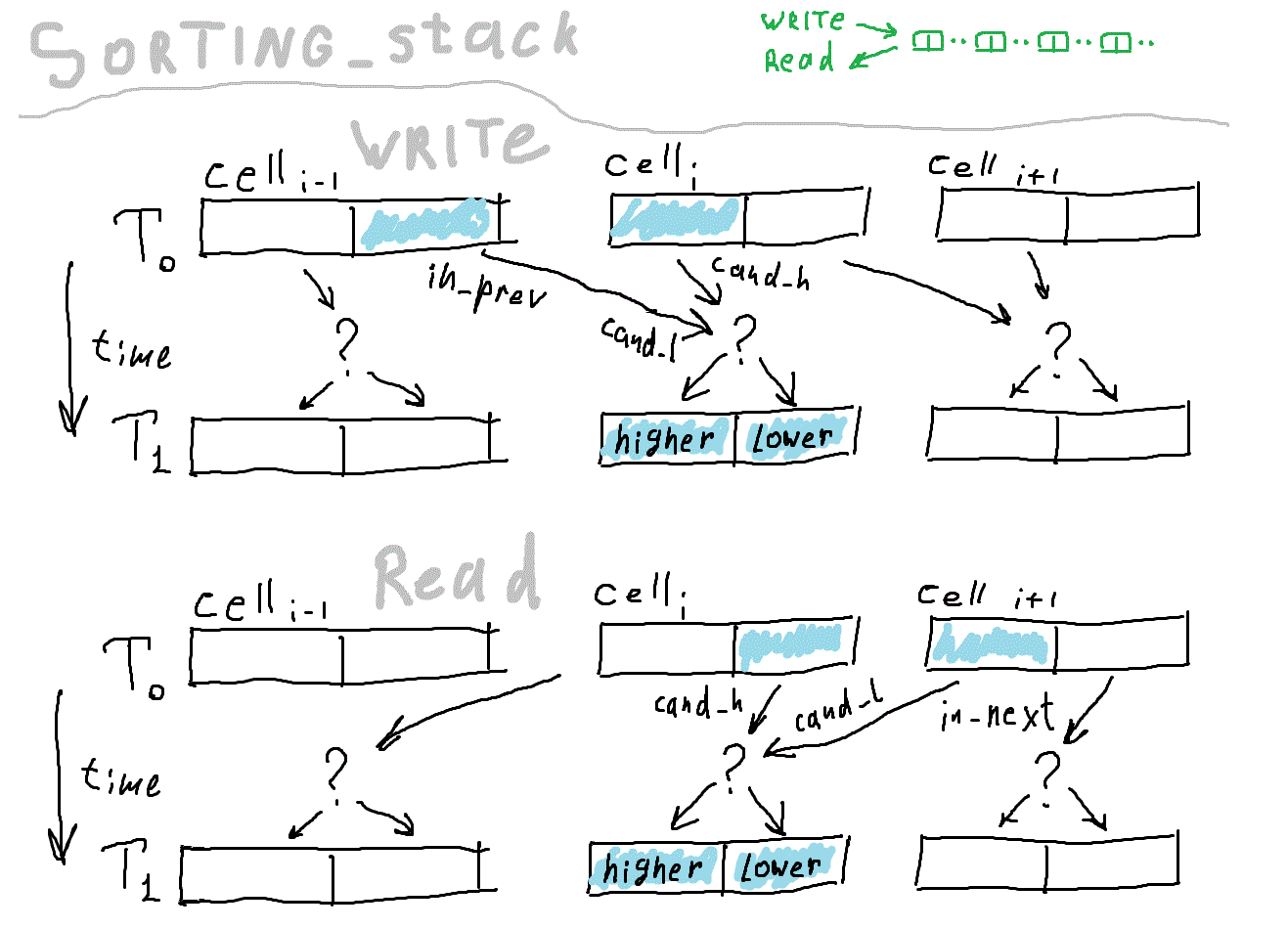
Посмотрим на исходники на verilog-е. Напомню главное отличие HDL от языка программирования — язык программирования это инструкция для исполнителя, которая исполняется последовательно, строчка за строчкой, а программа на HDL соответствует электронной схеме, все части которой работают одновременно.
Разберём исходник сортировщика - цепочки.
Определяем модуль всей цепочки. у него есть входы, выходы и внутренние модули, всё это надо связать в единую сеть с помощью комбинационной схемы. Регистров тут в явном виде нет, они инкапсулированы внутри сортировочных ячеек.
Рассмотрим подробнее подстановку одного модуля в другой
Cell_Compare — тип модуля
#(HBIT) — установка числовых параметров
ribbon — имя экземпляра
[_R_SZ] — это массив, указываем количество
( clk, hold, is_input, — общие сигналы для всех
in_prev, in_next, out ); — специфические сигналы для каждого элемента массива.
Далее generate — полезная конструкция, которая позволяет
применять циклы и т.д. при описании комбинационных схем.
Теперь модуль сортировочной ячейки.
Здесь начинается собственно логика сортировки. Каждая ячейка хранит два числа, одно меньше другого. Каждый такт (если не hold) ячейка сравнивает число, пришедшее от соседа со своим «чемпионом». Чемпион — максимальное число при записи и минимальное при чтении. Проигравший покинет ячейку на следующем такте. В результате, данные движутся по цепочке сначала в одном направлении, потом в другом. Количество чисел, помещающихся в устройстве равно удвоенному количеству ячеек.
Вернёмся к исходному коду. Здесь при описании выхода применён селектор, (скомпилируется в мультиплексор). is_input определяет, читаем мы данные или пишем, от него зависит, в каком направлении движутся данные по цепочке.
Всё.
// Заголовок
module Sorting_Stack ( clk, hold, is_input, data_in, data_out );
// Числовые параметры
parameter HBIT= 15; // size of number in bits
parameter R_SZ= 256; // capacity, max sequence size
parameter _R_SZ= (R_SZ+1)/2; // not to modify
// Перечисляем входы-выходы схемы
// Тактовый сигнал
input clk;
...
// входы-выходы данных
input [HBIT:0] data_in; // load one number per clock
output [HBIT:0] data_out; // while is_input==0, max value popping out here
// в квадратных скобках перед именем - разрядность
...
// Промежуточные точки схемы
wire [HBIT:0] in_prev[_R_SZ];
wire [HBIT:0] in_next[_R_SZ];
wire [HBIT:0] out[_R_SZ];
// в квадратных скобках после имени - размерности массивов
// Внутренние подмодули модуля
// Здесь определён целый массив подмодулей
// storage
Cell_Compare #(HBIT) ribbon[_R_SZ] ( clk, hold, is_input, in_prev, in_next, out );
Рассмотрим подробнее подстановку одного модуля в другой
Cell_Compare — тип модуля
#(HBIT) — установка числовых параметров
ribbon — имя экземпляра
[_R_SZ] — это массив, указываем количество
( clk, hold, is_input, — общие сигналы для всех
in_prev, in_next, out ); — специфические сигналы для каждого элемента массива.
Далее generate — полезная конструкция, которая позволяет
применять циклы и т.д. при описании комбинационных схем.
// Соединяем некоторые точки схемы
generate
genvar i,j;
for (i=0; i<_R_SZ-1; i=i+1)
begin : block_name01
assign in_prev[i+1]= out[i];
assign in_next[i]= out[i+1];
end
assign in_prev[0]= data_in;
assign data_out= out[0];
assign in_next[_R_SZ-1]= 0;
endgenerate
endmodule
Теперь модуль сортировочной ячейки.
module Cell_Compare ( clk, hold, is_input, in_prev, in_next, out );
parameter HBIT= 15;
input clk;
input hold;
input is_input;
input [HBIT:0] in_prev;
input [HBIT:0] in_next;
Здесь начинается собственно логика сортировки. Каждая ячейка хранит два числа, одно меньше другого. Каждый такт (если не hold) ячейка сравнивает число, пришедшее от соседа со своим «чемпионом». Чемпион — максимальное число при записи и минимальное при чтении. Проигравший покинет ячейку на следующем такте. В результате, данные движутся по цепочке сначала в одном направлении, потом в другом. Количество чисел, помещающихся в устройстве равно удвоенному количеству ячеек.
Вернёмся к исходному коду. Здесь при описании выхода применён селектор, (скомпилируется в мультиплексор). is_input определяет, читаем мы данные или пишем, от него зависит, в каком направлении движутся данные по цепочке.
output [HBIT:0] out= is_input ? lower : higher;
// Хранилище. Это все регистры, что есть в сортировщике
bit [HBIT:0] higher;
bit [HBIT:0] lower;
// Здесь определяется, что будет в хранилище на следующем такте.
// В зависимости от направления движения данных, это будет
// либо higher и in_prev (lower выталкивается к хвосту),
// либо lower и in_next (higher выталкивается к голове)
wire [HBIT:0] cand_h= is_input ? higher : lower;
wire [HBIT:0] cand_l= is_input ? in_prev : in_next;
// Далее описывается синхронная логика.
// В отличие от комбинационной схемы, от времени не зависещей,
// в регистры можно писать только в определённые моменты.
always@(posedge clk )
if (~hold)
begin
// Здесь мы наконец сравниваем два числа-кандидата.
higher <= ( cand_h >= cand_l ) ? cand_h : cand_l;
lower <= ( cand_h >= cand_l ) ? cand_l : cand_h;
end
endmodule
Всё.
Но я сделал ещё одну реализацию с таким же интерфейсом, но немного другими свойствами. Различия реализаций: Первая на основе цепочки сортирующих ячеек, вторая на основе двоичного дерева, в узлах которого такие же ячейки.
Первая реализация позволяет дописывать данные в частично опустошённый буфер (можно, например, сортировать запросы на прерывания по приоритету), древовидная после записи требует полного прочтения.
Преимущество древовидной реализации — в процессе работы двигается не вся цепочка, а только одна ветка — теоретически более энергоэффективно.
Древовидная реализация
использует рекурсию для описания двоичного дерева, я даже не ожидал, что это сработает на verilog-е. Приведу только образец рекурсивного определения дерева.
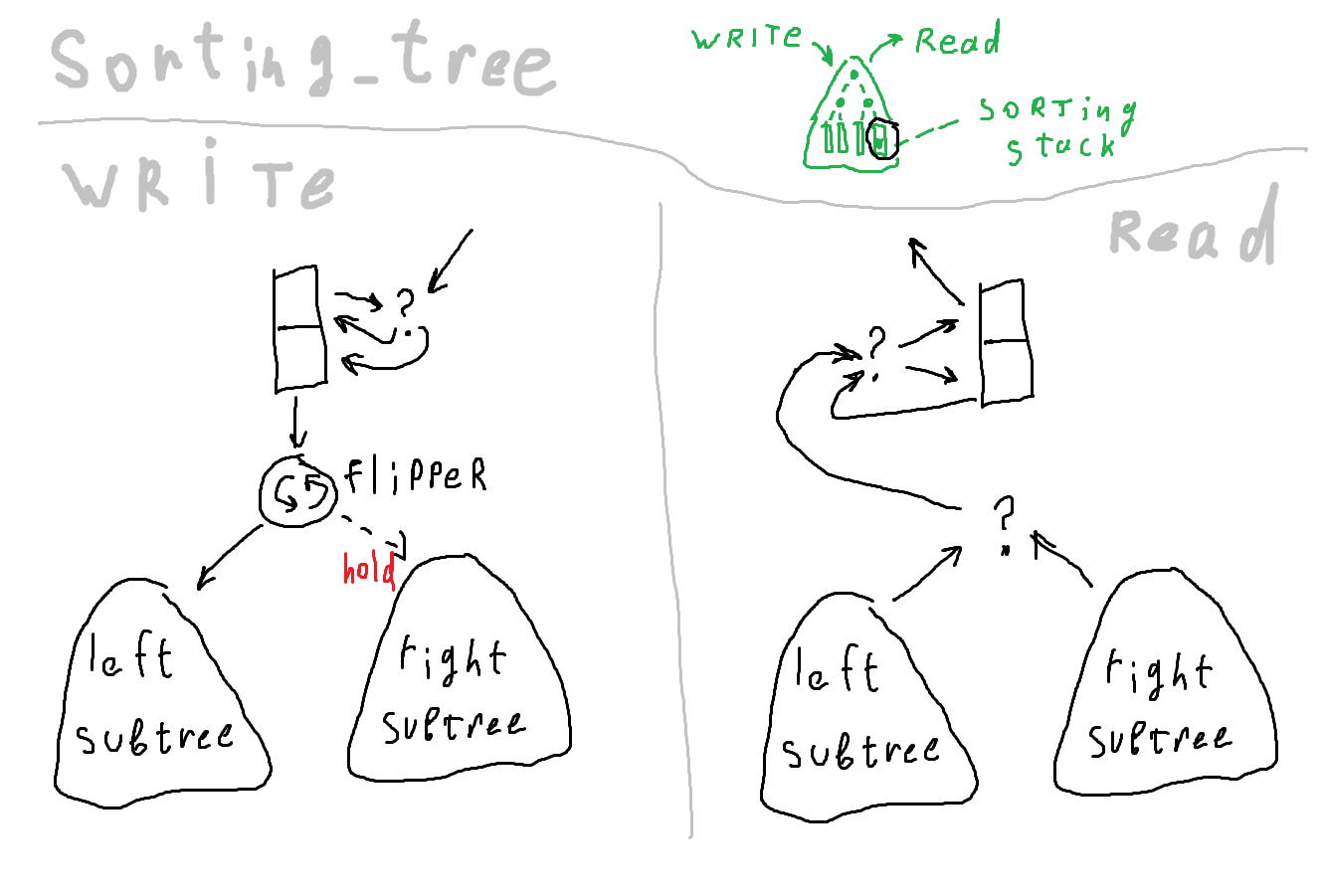
Логика движения данных по дереву такая: при записи ветви выбираются поочерёдно. При чтении нужно сделать дополнительное сравнение, чтобы определить, в корне какого поддерева число больше. В результате дереву нужно больше компараторов по сравнению с цепочкой того же объёма. Преимущество дерева в том, что данные меньше движутся, а энергопотребление схемы сильно зависит от количества переключений состояния регистров.
module NodeType ( );
endmodule
module TreeTemplate ( );
parameter TREE_LEVEL= 4;
NodeType node();
generate
if ( TREE_LEVEL >0 )
begin
TreeTemplate #( TREE_LEVEL-1 ) leftSubtree ( );
TreeTemplate #( TREE_LEVEL-1 ) rightSubtree ( );
end
endgenerate
endmodule
Логика движения данных по дереву такая: при записи ветви выбираются поочерёдно. При чтении нужно сделать дополнительное сравнение, чтобы определить, в корне какого поддерева число больше. В результате дереву нужно больше компараторов по сравнению с цепочкой того же объёма. Преимущество дерева в том, что данные меньше движутся, а энергопотребление схемы сильно зависит от количества переключений состояния регистров.
Соответствующая картинка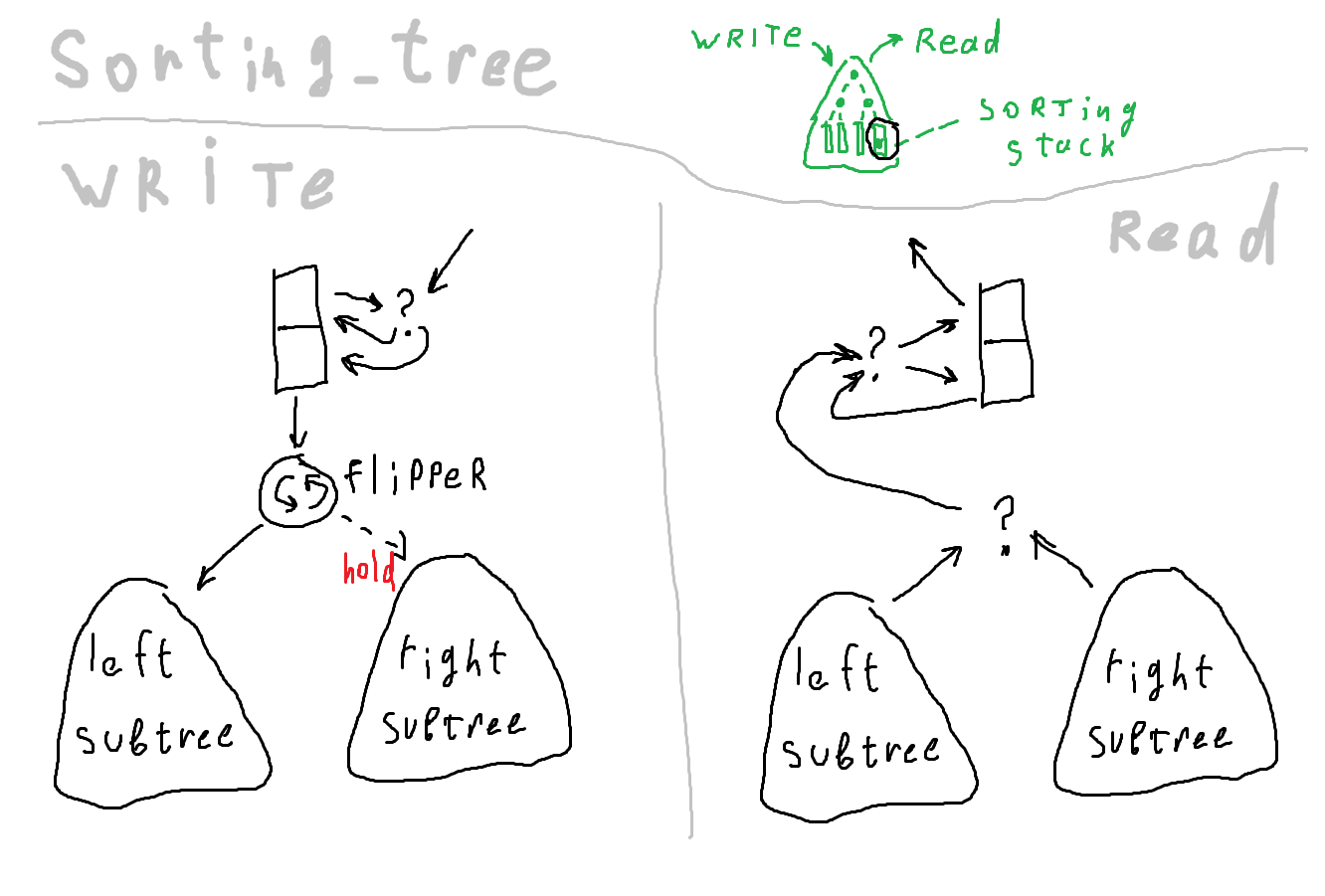
Вообще-то, рекурсивные определения модулей это очень нехарактерный стиль для верилога. Должен признаться, данный проект — «паровоз для машиниста». Правильный подход таков, — задана цель написать сортировщик, мы выбираем реализацию — дерево. В моём же случае, сама идея написать сортировщик возникла из необходимости освоить работу с древовидными структурами, — для нужд вычислителя на базе комбинаторной логики. Я уже немного написал об этом проекте в конце своего предыдущего, первого на Хабре поста. Работа машины сводится к вычислению комбинаторного выражения методом параллельного переписывания термов. Основная идея — сопоставить дереву функциональной программы аппаратное дерево ячеек, способных применять комбинаторы. Теоретически, так можно эффективно решать задачи из булевой алгебры или исчисления предикатов, для целей символьных вычислений или доказательства теорем. Надеюсь, в ближайшие месяцы у меня будет готова работающая версия, способная редуцировать простенькие выражения. Если вам известны какие-нибудь практические задачи, хорошо ложащиеся на чистое лямбда исчисление или комбинаторную логику, напишите, пожалуйста, в комментариях.
Исходники модулей сортировщиков здесь под LGPL, есть тестовые проекты для плат Марсоход2, Terasic DE0 и DE2-115.
p.s. прошу прощения за пересоздание топика. Теперь я знаю, что нельзя убирать свежеопубликованный топик в черновики надолго в первые сутки.