В этой публикации речь пойдет о подходах к построению перцептивный хешей изображения и возможностях их использования (например, поиск дубликатов).
перцептивный хэш-алгоритмы описывают класс функций для генерации сравнимых хэшей. Они используют различные свойства изображения для построения индивидуального «отпечатка». В дальнейшем эти «отпечатки» можно сравнивать друг с другом.
Если хэши отличаются, значит, данные разные. Если хэши совпадают, то данные, скорее всего, одинаковые (поскольку существует вероятность коллизий, то одинаковые хэши не гарантируют совпадения данных). В этой статье речь пойдет о нескольких популярных методах построения перцептивный хешей изображения, а также о простом способе борьбы с коллизиями. Всем кому интересно, прошу под кат.
Существует много различных подходов к формированию перцептивный хеша изображения. Всех их объединяет 3 основных этапа:
В данной публикации мы не будем касаться реализации приведенных алгоритмов. Она носит обзорный характер и рассказывает о различных подходах к построению хэшей.
Мы будем рассматривать 4 различных хеш алгоритма: Simple Hash[4], DCT Based Hash[1],[11], Radial Variance Based Hash[1],[5] и Marr- Hildreth Operator Based Hash[1],[6].
Суть данного алгоритма заключается в отображении среднего значения низких частот. В изображениях высокие частоты обеспечивают детализацию, а низкие – показывают структуру. Поэтому для построения такой хеш-функции, которая для похожих изображений будет выдавать близкий хеш, нужно избавиться от высоких частот. Принцип работы:
Полученный хеш устойчив к масштабированию, сжатию или растягиванию изображения, изменению яркости, контраста, манипуляциями с цветами. Но главное достоинство алгоритма – скорость работы. Для сравнения хешей этого типа используется функция нормированного расстояния Хэмминга.

Исходное изображение

Полученный «отпечаток»
Дискретное косинусное преобразование (ДКП, DCT) [7] – одно из ортогональных преобразований, тесно связанное с дискретным преобразованием Фурье (ДПФ) и являющееся гомоморфизмом его векторного пространства. ДКП, как и любое Фурье-ориентированное преобразование, выражает функцию или сигнал (последовательность из конечного числа точек данных) в виде суммы синусоид с различными частотами и амплитудами. ДКП использует только косинусные функции, в отличие от ДПФ, использующего и косинусные, и синусные функции. Существует 8 типов ДКП [7]. Самый распространенный – второй тип. Его мы и будем использовать для построения хеш-функции.
Давайте разберемся, что такое второй тип ДКП:
Пусть x[m], где m = 0,…, N — 1 — последовательность сигнала длин N. Определим второй тип ДКП, как
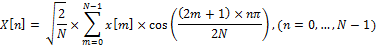
Это выражение можно переписать как:
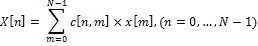
где c[n,m] – элемент матрицы ДКП на пересечении строки с номером n и столбца с номером m.
ДКП матрица определяется как:

Данная матрица очень удобна, для вычисления ДКП. ДКП может быть вычислена заранее, для любой необходимой длины. Таким образом ДКП может быть представлена в виде:
ДКП=M×I×M'
Где M – ДКП матрица, I – изображение квадратного размера, M’ – обратная матрица.
Низкочастотные коэффициенты ДКП наиболее стабильны к манипуляциям с изображениями. Это происходит потому, что большая часть информации сигнала, как правило, сосредоточена в нескольких низкочастотных коэффициентах. В качестве матрицы I обычно берется изображение, сжатое до размера 32х32 и упрощенное с помощью различных фильтров, например, обесцвечивания. В итоге получается матрица ДКП (I), в левом верхнем углу которой и находятся низкочастотные коэффициенты. Чтобы построить хеш берется левый верхний блок частот 8x8. Затем из этого блока строится хеш размером 8 байт с помощью нахождения среднего и построения цепочки бит (также, как в Simple Based Hash).
Перечислим шаги построения хеша с помощью данного алгоритма:
Главные преимущества такого хеша: устойчивость к малым поворотам, размытию и сжатию изображения, а также скорость сравнения хешей, благодаря их маленькому размеру. Для сравнения хешей этого типа используется функция расстояния Хэмминга.
Идея алгоритма Radial Variance Based Hash состоит в построении лучевого вектора дисперсии (ЛВД) на основе преобразования Радона [5]. Затем к ЛВД применяется ДКП и вычисляется хеш. Преобразование Радона — это интегральное преобразование функции многих переменных вдоль прямой. Оно устойчиво к обработке изображений с помощью различных манипуляций (например, сжатия) и геометрических преобразований (например, поворотов). В двумерном случае преобразование Радона для функции f(x,y) выглядит так:
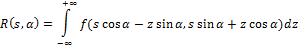
Преобразование Радона имеет простой геометрический смысл – это интеграл от функции вдоль прямой, перпендикулярной вектору n = (cos a,sin a) и проходящей на расстоянии s (измеренного вдоль вектора n, с соответствующим знаком) от начала координат.
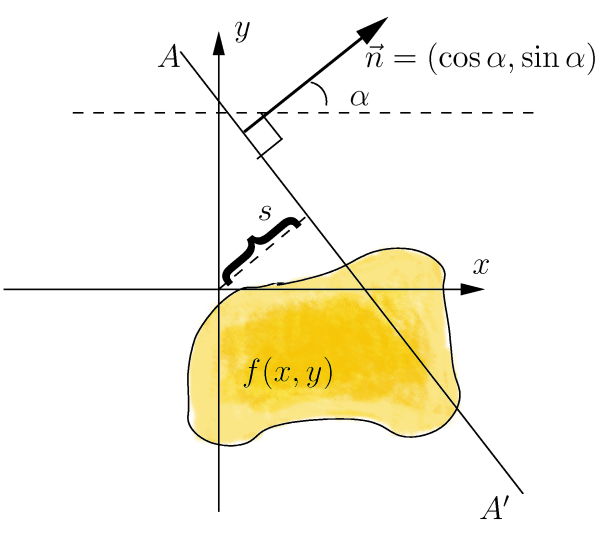
Чтобы преобразование Радона расширить для дискретных изображений, линейный интеграл по прямой d = x ∙ cos α + y ∙ sin α может быть аппроксимирован путем суммирования значений всех пикселей, лежащих в линии шириной один пиксель:

Позже было обнаружено, что лучше использовать дисперсию вместо суммы значений пикселей вдоль линии проекции [6]. Дисперсия намного лучше обрабатывает яркостные разрывы вдоль линии проекции. Такие яркостные разрывы появляются из-за краев, которые ортогональны линии проекции.
Теперь определим лучевой вектор дисперсии. Пусть Г(α) – набор пикселей на линии проекции, соответствующей данному углу. Пусть (x′, y′) – координаты центрального пикселя на изображении. x, y принадлежат Г(α) тогда и только тогда, когда
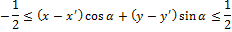
Теперь определим лучевой вектор дисперсии (radial variance vector):
Пусть I(x,y) обозначает яркость пикселя (x,y), #Г(α) – мощность множества, тогда лучевой вектор дисперсии R[α], где α = 0,1, … ,179 определим как
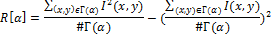
Достаточно построить вектор по 180 значениям угла, так как преобразование Радона является симметричным. Полученный вектор можно использовать для построения хеша, но в этом алгоритме предлагается еще некоторое улучшение — применить ДКП к полученному вектору. В результате получится вектор, наследующий все важные свойства ДКП. В качестве хеша берутся первые 40 коэффициентов полученного вектора, которые соответствуют низким частотам. Таким образом, размер полученного хеша — 40 байт.
Итак, перечислим шаги построения хеша с помощью данного алгоритма:
Для сравнения хешей этого типа используется поиск пика взаимнокорреляционной функции.
Оператор Марра-Хилдрета [16] позволяет определять края на изображении. Вообще говоря, границу на изображении можно определить как край или контур, отделяющий соседние части изображения, которые имеют сравнительно отличные характеристики в соответствии с некоторыми особенностями. Этими особенностями могут быть цвет или текстура, но чаще всего используется серая градация цвета изображения (яркость). Результатом определения границ является карта границ. Карта границ описывает классификацию границ для каждого пикселя изображения. Если границы определять как резкое изменение яркости, то для их нахождения можно использовать производные или градиент.
Пусть функция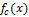 обозначает уровень яркости для линии (одномерный массив пикселей). Первый подход определения границ заключается в нахождении локальных экстремумов функции, то есть первых производных. Второй подход (метод Лапласа) заключается в нахождении вторых производных
обозначает уровень яркости для линии (одномерный массив пикселей). Первый подход определения границ заключается в нахождении локальных экстремумов функции, то есть первых производных. Второй подход (метод Лапласа) заключается в нахождении вторых производных 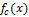 [1].
[1].
Оба подхода могут быть адаптированы для случая двумерных дискретных изображений, но с некоторыми проблемами. Для нахождения производных в дискретном случае требуется аппроксимация. Кроме того, шум на изображении может значительно ухудшить процесс поиска границ. Поэтому перед определением границ к изображению нужно применить какой-либо фильтр, подавляющий шумы. Для построения хеша можно выбрать алгоритм, использующий оператор Лапласа (2 подход) и фильтр Гаусса.
Определим непрерывный Лапласиан (оператор Лапласа):
Пусть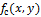 определяет яркость на изображении. Тогда непрерывный Лапласиан определим как:
определяет яркость на изображении. Тогда непрерывный Лапласиан определим как:
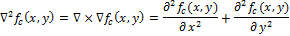
Обращения в ноль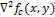 и есть точки, соответствующие границе функции
и есть точки, соответствующие границе функции 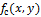 , так как это точки, при которых вторая производная обращается в ноль. Различные фильтры (дискретные операторы Лапласа) могут быть получены из непрерывного Лапласиана. Такой фильтр
, так как это точки, при которых вторая производная обращается в ноль. Различные фильтры (дискретные операторы Лапласа) могут быть получены из непрерывного Лапласиана. Такой фильтр  , может быть применен к дискретному изображению с помощью использования свертки функций. Оператор Лапласа для изображения
, может быть применен к дискретному изображению с помощью использования свертки функций. Оператор Лапласа для изображения 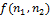 можно переписать как:
можно переписать как:
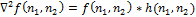
где * обозначает свертку функций. Чтобы построить карту границ, нужно найти обращения в ноль дискретного оператора .
.
Теперь рассмотрим оператор Марра-Хилдрета. Он также называется Лапласиан от фильтра Гаусса (LoG) – это особенный тип дискретного оператора Лапласа. LoG конструируется с помощью применения оператора Лапласа к фильтру (функции) Гаусса. Особенность этого оператора в том, что он может выделять границы в определенном масштабе. Переменную масштаба можно варьировать для того, чтобы лучше выявить границы.
Фильтр Гаусса определим как:
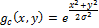
Свертку с операцией Лапласа можно поменять местами, потому что производная и свертка – линейные операторы:
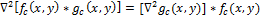
Это свойство позволяет заранее вычислить оператор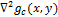 , потому что он никак не зависит от изображения (
, потому что он никак не зависит от изображения (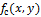 ).
).
(оператор Марра-Хилдрета, Лапласиан от фильтра Гаусса, LoG). LoG hc(x, y) определим как:
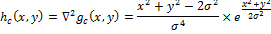
Чтобы использовать LoG в дискретной форме, сделаем дискретизацию данного уравнения, подставив нужную переменную масштаба. По умолчанию ее значение принимается как 1.0. Затем фильтр можно применить к изображению, используя дискретную свертку.
Определим дискретную свертку:
Пусть x,y,z — пиксельная ширина, длина и глубина изображения I.
Результат R свертки изображения I c маской M определим как:
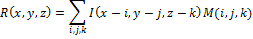
Теперь перечислим шаги алгоритма, использующего для построения хеша оператор Марра-Хилдрета:
Размер полученного хеша не маленький, тем не менее, сравнение двух хешей занимает достаточно незначительное время по сравнению с Radial алгоритмом, так как используется функция нормированного расстояния Хэмминга. Также такой алгоритм чувствителен к поворотам изображения, но устойчив к масштабированию, затемнению, сжатию.
Расстояние Хэмминга определяет количество различных позиций между двумя бинарными последовательностями.
Определение:
Пусть А – алфавит конечной длины.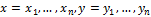 – бинарные последовательности (векторы). Расстояние Хэмминга Δ между x и y определим как:
– бинарные последовательности (векторы). Расстояние Хэмминга Δ между x и y определим как:
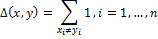
Этот способ сравнения хеш-значений используется в методе DCT Based Hash. Хеш занимает размер 8 байт, поэтому расстояние Хэмминга лежит в отрезке [0, 64]. Чем меньше значение Δ, тем более похожи изображения.
Для облегчения сравнения расстояние Хэмминга можно нормировать с помощью длины векторов:
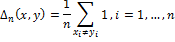
Нормированное расстояние Хэмминга используется в алгоритмах Simple Hash и Marr-Hildreth Operator Based Hash. Расстояние Хэмминга лежит в промежутке [0,1] и чем ближе Δ к 0, тем более похожи изображения.
Корреляцию между двумя сигналами определим как:

где x(t) и y(t) — две непрерывные функции вещественных чисел. Функция rxy(t) описывает смещение этих двух сигналов относительно времени T. Переменная T определяет насколько сигнал смещен слева. Если сигналы x(t) и y(t) различны, функция rxy T называется взаимнокорреляционной.
Определим Нормированную взаимнокорреляционную функцию:
Пусть xi и yi, где i = 0, … N − 1 – две последовательности вещественных чисел, а N – длина обеих последовательностей. НВФ с задержкой d определим как:
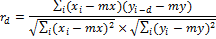
где mx и my обозначают среднее значение для соответствующей последовательности.
Пик взаимнокорреляционной функции (PCC) – максимальное значение функции rd, которое может быть достигнуто на промежутке d = 0, N.
PCC используется для сравнения хеш-значений в алгоритме Radial Variance Based Hash. PCC ∈ [0,1], чем больше его значение, тем более похожи изображения.
Мы рассмотрели 4 различных подхода в реализации хеш алгоритмов. Областей применения перцептивный хешей широк, от поиска похожих изображений, до выявления спама на картинках.
В своем проекте мы используем перцептивный хеш для выявления дубликатов изображений. При этом зачастую удается успешно сравнивать между собой изображения, содержащие watermark’и (полученные из разных источников) или изображения с обрезанными краями.
Лучшим алгоритмом для поиска дубликатов можно считать Radial Variance Based Hash, однако его крайне трудно применять на больших объемах данных, из-за очень трудоемкого сравнения хешей.
Для себя мы выбрали DCT based Hash. Мы используем 64 битный хэш, этого вполне хватает для поиска дубликатов, однако столь малый размер хеша неизбежно приводит к коллизиям. С коллизиями мы боремся построением гистограммы (спектра) для изображения.
Каждая компонента спектра означает относительное количество цветов того или иного под диапазона в изображении, другими словами показывает распределение цветов по изображению. Выглядит это примерно вот так:

Таким образом, мы сначала ищем изображения сравнивая хеш, а потом сравниваем гистограммы, если гистограммы значительно отличаются, то такое изображение не считается похожим. Сами гистограммы можно сравнивать считая взаимную корреляцию также, как при сравнении Radial Variance Based Hash, с помощью взаимной корреляции Пирсона:
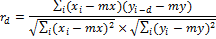
Если данная тема интересна сообществу, в следующей статье я расскажу конкретно о нашей реализации DCT hash, а также о способах поиска дистанции Хемминга.
перцептивный хэш-алгоритмы описывают класс функций для генерации сравнимых хэшей. Они используют различные свойства изображения для построения индивидуального «отпечатка». В дальнейшем эти «отпечатки» можно сравнивать друг с другом.
Если хэши отличаются, значит, данные разные. Если хэши совпадают, то данные, скорее всего, одинаковые (поскольку существует вероятность коллизий, то одинаковые хэши не гарантируют совпадения данных). В этой статье речь пойдет о нескольких популярных методах построения перцептивный хешей изображения, а также о простом способе борьбы с коллизиями. Всем кому интересно, прошу под кат.
Обзор
Существует много различных подходов к формированию перцептивный хеша изображения. Всех их объединяет 3 основных этапа:
- Предварительная обработка. На этой стадии изображение приводится к виду, в котором его легче обрабатывать для построения хеша. Это может быть применение различных фильтров (например, Гаусса), обесцвечивание, уменьшение размеров изображения и т.д.
- Основные вычисления. Из полученного на 1 стадии изображения строится матрица (или вектор). Матрица (вектор) может представлять из себя матрицу частот (например, после преобразования Фурье), гистограмму яркостей, или еще более упрощенное изображение.
- Построение хеша. Из матрицы (вектора), полученной на 2 стадии берутся некоторые (возможно все) коэффициенты и преобразуются в хеш. Обычно хеш получается размером от 8 до ~100 байт. Вычисленные значения хешей затем сравниваются с помощью функций, вычисляющих «расстояние» между двумя хешами.
В данной публикации мы не будем касаться реализации приведенных алгоритмов. Она носит обзорный характер и рассказывает о различных подходах к построению хэшей.
Перцептивные хеш-алгоритмы
Мы будем рассматривать 4 различных хеш алгоритма: Simple Hash[4], DCT Based Hash[1],[11], Radial Variance Based Hash[1],[5] и Marr- Hildreth Operator Based Hash[1],[6].
Simple Hash (a.k.a Average Hash)
Суть данного алгоритма заключается в отображении среднего значения низких частот. В изображениях высокие частоты обеспечивают детализацию, а низкие – показывают структуру. Поэтому для построения такой хеш-функции, которая для похожих изображений будет выдавать близкий хеш, нужно избавиться от высоких частот. Принцип работы:
- Уменьшить размер. Самый быстрый способ избавиться от высоких частот — уменьшить изображение. Изображение уменьшается до размера в диапазоне 32х32 и 8х8.
- Убрать цвет. Маленькое изображение переводится в градации серого, таким образом хеш уменьшается втрое.
- Вычислить среднее значение цвета для всех пикселей.
- Построить цепочку битов. Для каждого пикселя делается замена цвета на 1 или 0 в зависимости от того, больше он или меньше среднего.
- Построить хеш. Перевод 1024 битов в одно значение. Порядок не имеет значения, но обычно биты записываются слева направо, сверху вниз.
Полученный хеш устойчив к масштабированию, сжатию или растягиванию изображения, изменению яркости, контраста, манипуляциями с цветами. Но главное достоинство алгоритма – скорость работы. Для сравнения хешей этого типа используется функция нормированного расстояния Хэмминга.

Исходное изображение

Полученный «отпечаток»
Discrete Cosine Transform Based Hash (a.k.a. pHash)
Дискретное косинусное преобразование (ДКП, DCT) [7] – одно из ортогональных преобразований, тесно связанное с дискретным преобразованием Фурье (ДПФ) и являющееся гомоморфизмом его векторного пространства. ДКП, как и любое Фурье-ориентированное преобразование, выражает функцию или сигнал (последовательность из конечного числа точек данных) в виде суммы синусоид с различными частотами и амплитудами. ДКП использует только косинусные функции, в отличие от ДПФ, использующего и косинусные, и синусные функции. Существует 8 типов ДКП [7]. Самый распространенный – второй тип. Его мы и будем использовать для построения хеш-функции.
Давайте разберемся, что такое второй тип ДКП:
Пусть x[m], где m = 0,…, N — 1 — последовательность сигнала длин N. Определим второй тип ДКП, как
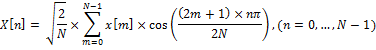
Это выражение можно переписать как:
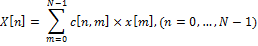
где c[n,m] – элемент матрицы ДКП на пересечении строки с номером n и столбца с номером m.
ДКП матрица определяется как:
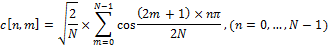
Данная матрица очень удобна, для вычисления ДКП. ДКП может быть вычислена заранее, для любой необходимой длины. Таким образом ДКП может быть представлена в виде:
ДКП=M×I×M'
Где M – ДКП матрица, I – изображение квадратного размера, M’ – обратная матрица.
Низкочастотные коэффициенты ДКП наиболее стабильны к манипуляциям с изображениями. Это происходит потому, что большая часть информации сигнала, как правило, сосредоточена в нескольких низкочастотных коэффициентах. В качестве матрицы I обычно берется изображение, сжатое до размера 32х32 и упрощенное с помощью различных фильтров, например, обесцвечивания. В итоге получается матрица ДКП (I), в левом верхнем углу которой и находятся низкочастотные коэффициенты. Чтобы построить хеш берется левый верхний блок частот 8x8. Затем из этого блока строится хеш размером 8 байт с помощью нахождения среднего и построения цепочки бит (также, как в Simple Based Hash).
Перечислим шаги построения хеша с помощью данного алгоритма:
- Убрать цвет. Для подавления ненужных высоких частот;
- Применить медианный фильтр [8] для уменьшения уровня шума. При этом, изображение разбивается на так называемые «окна», затем каждое окно заменяется медианой [9] для соседних окон;
- Уменьшить изображение до размера 32x32;
- Применить ДКП к изображению;
- Построить хеш.
Главные преимущества такого хеша: устойчивость к малым поворотам, размытию и сжатию изображения, а также скорость сравнения хешей, благодаря их маленькому размеру. Для сравнения хешей этого типа используется функция расстояния Хэмминга.
Radial Variance Based Hash
Идея алгоритма Radial Variance Based Hash состоит в построении лучевого вектора дисперсии (ЛВД) на основе преобразования Радона [5]. Затем к ЛВД применяется ДКП и вычисляется хеш. Преобразование Радона — это интегральное преобразование функции многих переменных вдоль прямой. Оно устойчиво к обработке изображений с помощью различных манипуляций (например, сжатия) и геометрических преобразований (например, поворотов). В двумерном случае преобразование Радона для функции f(x,y) выглядит так:
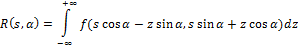
Преобразование Радона имеет простой геометрический смысл – это интеграл от функции вдоль прямой, перпендикулярной вектору n = (cos a,sin a) и проходящей на расстоянии s (измеренного вдоль вектора n, с соответствующим знаком) от начала координат.
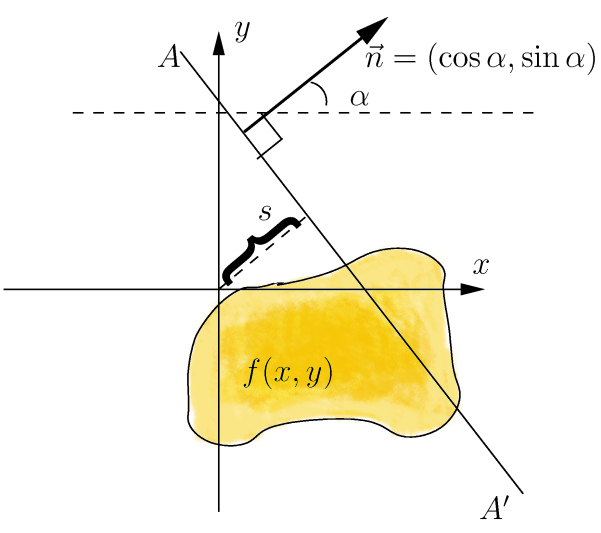
Чтобы преобразование Радона расширить для дискретных изображений, линейный интеграл по прямой d = x ∙ cos α + y ∙ sin α может быть аппроксимирован путем суммирования значений всех пикселей, лежащих в линии шириной один пиксель:
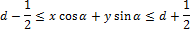
Позже было обнаружено, что лучше использовать дисперсию вместо суммы значений пикселей вдоль линии проекции [6]. Дисперсия намного лучше обрабатывает яркостные разрывы вдоль линии проекции. Такие яркостные разрывы появляются из-за краев, которые ортогональны линии проекции.
Теперь определим лучевой вектор дисперсии. Пусть Г(α) – набор пикселей на линии проекции, соответствующей данному углу. Пусть (x′, y′) – координаты центрального пикселя на изображении. x, y принадлежат Г(α) тогда и только тогда, когда
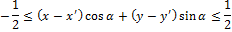
Теперь определим лучевой вектор дисперсии (radial variance vector):
Пусть I(x,y) обозначает яркость пикселя (x,y), #Г(α) – мощность множества, тогда лучевой вектор дисперсии R[α], где α = 0,1, … ,179 определим как
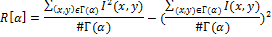
Достаточно построить вектор по 180 значениям угла, так как преобразование Радона является симметричным. Полученный вектор можно использовать для построения хеша, но в этом алгоритме предлагается еще некоторое улучшение — применить ДКП к полученному вектору. В результате получится вектор, наследующий все важные свойства ДКП. В качестве хеша берутся первые 40 коэффициентов полученного вектора, которые соответствуют низким частотам. Таким образом, размер полученного хеша — 40 байт.
Итак, перечислим шаги построения хеша с помощью данного алгоритма:
- Убрать цвет для подавления ненужных высоких частот;
- Размыть изображение (blurring) с помощью использования Гауссова размытия [10]. Изображение преобразуется с помощью функции Гаусса для подавления некоторых шумов;
- Применить гамма-коррекцию для устранения блеклости изображения.
- Построить лучевой вектор дисперсии;
- Применить ДКП к вектору дисперсии;
- Построить хеш.
Для сравнения хешей этого типа используется поиск пика взаимнокорреляционной функции.
Marr-Hildreth Operator Based Hash
Оператор Марра-Хилдрета [16] позволяет определять края на изображении. Вообще говоря, границу на изображении можно определить как край или контур, отделяющий соседние части изображения, которые имеют сравнительно отличные характеристики в соответствии с некоторыми особенностями. Этими особенностями могут быть цвет или текстура, но чаще всего используется серая градация цвета изображения (яркость). Результатом определения границ является карта границ. Карта границ описывает классификацию границ для каждого пикселя изображения. Если границы определять как резкое изменение яркости, то для их нахождения можно использовать производные или градиент.
Пусть функция
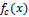 обозначает уровень яркости для линии (одномерный массив пикселей). Первый подход определения границ заключается в нахождении локальных экстремумов функции, то есть первых производных. Второй подход (метод Лапласа) заключается в нахождении вторых производных
обозначает уровень яркости для линии (одномерный массив пикселей). Первый подход определения границ заключается в нахождении локальных экстремумов функции, то есть первых производных. Второй подход (метод Лапласа) заключается в нахождении вторых производных 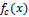 [1].
[1].Оба подхода могут быть адаптированы для случая двумерных дискретных изображений, но с некоторыми проблемами. Для нахождения производных в дискретном случае требуется аппроксимация. Кроме того, шум на изображении может значительно ухудшить процесс поиска границ. Поэтому перед определением границ к изображению нужно применить какой-либо фильтр, подавляющий шумы. Для построения хеша можно выбрать алгоритм, использующий оператор Лапласа (2 подход) и фильтр Гаусса.
Определим непрерывный Лапласиан (оператор Лапласа):
Пусть
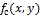 определяет яркость на изображении. Тогда непрерывный Лапласиан определим как:
определяет яркость на изображении. Тогда непрерывный Лапласиан определим как: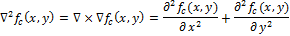
Обращения в ноль
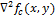 и есть точки, соответствующие границе функции
и есть точки, соответствующие границе функции 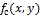 , так как это точки, при которых вторая производная обращается в ноль. Различные фильтры (дискретные операторы Лапласа) могут быть получены из непрерывного Лапласиана. Такой фильтр
, так как это точки, при которых вторая производная обращается в ноль. Различные фильтры (дискретные операторы Лапласа) могут быть получены из непрерывного Лапласиана. Такой фильтр 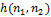 , может быть применен к дискретному изображению с помощью использования свертки функций. Оператор Лапласа для изображения
, может быть применен к дискретному изображению с помощью использования свертки функций. Оператор Лапласа для изображения 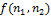 можно переписать как:
можно переписать как: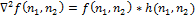
где * обозначает свертку функций. Чтобы построить карту границ, нужно найти обращения в ноль дискретного оператора
 .
.Теперь рассмотрим оператор Марра-Хилдрета. Он также называется Лапласиан от фильтра Гаусса (LoG) – это особенный тип дискретного оператора Лапласа. LoG конструируется с помощью применения оператора Лапласа к фильтру (функции) Гаусса. Особенность этого оператора в том, что он может выделять границы в определенном масштабе. Переменную масштаба можно варьировать для того, чтобы лучше выявить границы.
Фильтр Гаусса определим как:
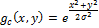
Свертку с операцией Лапласа можно поменять местами, потому что производная и свертка – линейные операторы:
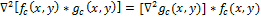
Это свойство позволяет заранее вычислить оператор
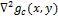 , потому что он никак не зависит от изображения (
, потому что он никак не зависит от изображения (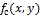 ).
).(оператор Марра-Хилдрета, Лапласиан от фильтра Гаусса, LoG). LoG hc(x, y) определим как:
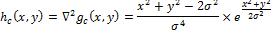
Чтобы использовать LoG в дискретной форме, сделаем дискретизацию данного уравнения, подставив нужную переменную масштаба. По умолчанию ее значение принимается как 1.0. Затем фильтр можно применить к изображению, используя дискретную свертку.
Определим дискретную свертку:
Пусть x,y,z — пиксельная ширина, длина и глубина изображения I.
Результат R свертки изображения I c маской M определим как:
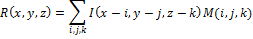
Теперь перечислим шаги алгоритма, использующего для построения хеша оператор Марра-Хилдрета:
- Убрать цвет для подавления ненужных высоких частот;
- Перевести изображение в размер 128x128;
- Размыть изображение(blurring). Изображение преобразуется с помощью функции Гаусса для подавления некоторых шумов [10];
- Построить оператор Марра-Хилдрета;
- Применить дискретную свертку к LoG и изображению. Получится
изображение, на котором четко видны скачки яркости; - Преобразовать изображение в гистограмму. Изображение разбивается на маленькие блоки(5x5), в которых суммируются значения яркостей.
- Построить хеш из гистограммы. Гистограмма разбивается на блоки 3x3. Для этих блоков считается среднее значение яркости и используется метод построения цепочки битов. Получается бинарный хеш размером 64 байта.
Размер полученного хеша не маленький, тем не менее, сравнение двух хешей занимает достаточно незначительное время по сравнению с Radial алгоритмом, так как используется функция нормированного расстояния Хэмминга. Также такой алгоритм чувствителен к поворотам изображения, но устойчив к масштабированию, затемнению, сжатию.
Функции сравнения перцептивных хеш-значений
Расстояние Хэмминга
Расстояние Хэмминга определяет количество различных позиций между двумя бинарными последовательностями.
Определение:
Пусть А – алфавит конечной длины.
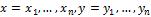 – бинарные последовательности (векторы). Расстояние Хэмминга Δ между x и y определим как:
– бинарные последовательности (векторы). Расстояние Хэмминга Δ между x и y определим как: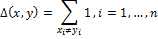
Этот способ сравнения хеш-значений используется в методе DCT Based Hash. Хеш занимает размер 8 байт, поэтому расстояние Хэмминга лежит в отрезке [0, 64]. Чем меньше значение Δ, тем более похожи изображения.
Для облегчения сравнения расстояние Хэмминга можно нормировать с помощью длины векторов:
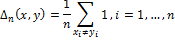
Нормированное расстояние Хэмминга используется в алгоритмах Simple Hash и Marr-Hildreth Operator Based Hash. Расстояние Хэмминга лежит в промежутке [0,1] и чем ближе Δ к 0, тем более похожи изображения.
Пик взаимнокорреляционной функции
Корреляцию между двумя сигналами определим как:
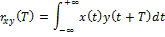
где x(t) и y(t) — две непрерывные функции вещественных чисел. Функция rxy(t) описывает смещение этих двух сигналов относительно времени T. Переменная T определяет насколько сигнал смещен слева. Если сигналы x(t) и y(t) различны, функция rxy T называется взаимнокорреляционной.
Определим Нормированную взаимнокорреляционную функцию:
Пусть xi и yi, где i = 0, … N − 1 – две последовательности вещественных чисел, а N – длина обеих последовательностей. НВФ с задержкой d определим как:
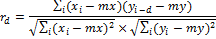
где mx и my обозначают среднее значение для соответствующей последовательности.
Пик взаимнокорреляционной функции (PCC) – максимальное значение функции rd, которое может быть достигнуто на промежутке d = 0, N.
PCC используется для сравнения хеш-значений в алгоритме Radial Variance Based Hash. PCC ∈ [0,1], чем больше его значение, тем более похожи изображения.
Несколько слов о практике
Мы рассмотрели 4 различных подхода в реализации хеш алгоритмов. Областей применения перцептивный хешей широк, от поиска похожих изображений, до выявления спама на картинках.
В своем проекте мы используем перцептивный хеш для выявления дубликатов изображений. При этом зачастую удается успешно сравнивать между собой изображения, содержащие watermark’и (полученные из разных источников) или изображения с обрезанными краями.
Лучшим алгоритмом для поиска дубликатов можно считать Radial Variance Based Hash, однако его крайне трудно применять на больших объемах данных, из-за очень трудоемкого сравнения хешей.
Для себя мы выбрали DCT based Hash. Мы используем 64 битный хэш, этого вполне хватает для поиска дубликатов, однако столь малый размер хеша неизбежно приводит к коллизиям. С коллизиями мы боремся построением гистограммы (спектра) для изображения.
Каждая компонента спектра означает относительное количество цветов того или иного под диапазона в изображении, другими словами показывает распределение цветов по изображению. Выглядит это примерно вот так:
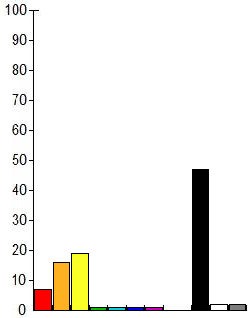
Таким образом, мы сначала ищем изображения сравнивая хеш, а потом сравниваем гистограммы, если гистограммы значительно отличаются, то такое изображение не считается похожим. Сами гистограммы можно сравнивать считая взаимную корреляцию также, как при сравнении Radial Variance Based Hash, с помощью взаимной корреляции Пирсона:
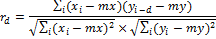
Если данная тема интересна сообществу, в следующей статье я расскажу конкретно о нашей реализации DCT hash, а также о способах поиска дистанции Хемминга.
Список литературы
[1] Egmont-Petersen, M., de Ridder, D., Handels, H. «Image processing with
neural networks — a review». Pattern Recognition 35 (10), pp. 2279–2301(2002)
[2] Christoph Zauner. Implementation and Benchmarking of Perceptual Image
Hash Functions (2010)
[3] Locality-sensitive hashing.
en.wikipedia.org/wiki/Locality-sensitive_hashing
[4] Simple and DCT perceptual hash-algorithms.
www.hackerfactor.com/blog/index.php?/archives/432-Looks-Like-
It.html
[5] Standaert, F.X., Lefebvre, F., Rouvroy, G., Macq, B.M., Quisquater, J.J.,
and Legat, J.D.: Practical evaluation of a radial soft hash algorithm. In
Proceedings of the International Symposium on Information Technology:
Coding and Computing (ITCC), vol. 2, pp. 89-94. IEEE, Apr. 2005
[6] D. Marrand, E. Hildret. Theory of edge detection, pp. 187-215 (1979)
[7] en.wikipedia.org/wiki/Discrete_cosine_transform
[8] en.wikipedia.org/wiki/Median_filter
[9] en.wikipedia.org/wiki/Median
[10] en.wikipedia.org/wiki/Gaussian_blur
[11] Zeng Jie. A Novel Block-DCT and PCA Based Image Perceptual Hashing
Algorithm. IJCSI International Journal of Computer Science Issues, Vol. 10,
Issue 1, No 3, January 2013
[12] de.wikipedia.org/wiki/Marr-Hildreth-Operator
neural networks — a review». Pattern Recognition 35 (10), pp. 2279–2301(2002)
[2] Christoph Zauner. Implementation and Benchmarking of Perceptual Image
Hash Functions (2010)
[3] Locality-sensitive hashing.
en.wikipedia.org/wiki/Locality-sensitive_hashing
[4] Simple and DCT perceptual hash-algorithms.
www.hackerfactor.com/blog/index.php?/archives/432-Looks-Like-
It.html
[5] Standaert, F.X., Lefebvre, F., Rouvroy, G., Macq, B.M., Quisquater, J.J.,
and Legat, J.D.: Practical evaluation of a radial soft hash algorithm. In
Proceedings of the International Symposium on Information Technology:
Coding and Computing (ITCC), vol. 2, pp. 89-94. IEEE, Apr. 2005
[6] D. Marrand, E. Hildret. Theory of edge detection, pp. 187-215 (1979)
[7] en.wikipedia.org/wiki/Discrete_cosine_transform
[8] en.wikipedia.org/wiki/Median_filter
[9] en.wikipedia.org/wiki/Median
[10] en.wikipedia.org/wiki/Gaussian_blur
[11] Zeng Jie. A Novel Block-DCT and PCA Based Image Perceptual Hashing
Algorithm. IJCSI International Journal of Computer Science Issues, Vol. 10,
Issue 1, No 3, January 2013
[12] de.wikipedia.org/wiki/Marr-Hildreth-Operator