При разработке игр часто возникает необходимость реализации следования некоторому маршруту. Например, персонажу нужно проложить путь из точки A в точку B. Допустим рассчитали его по какому-нибудь алгоритму поиска пути, идем. И тут оказывается, что из точки C в точку D идет другой юнит и пересекает нам дорогу и надо бы его обойти. Что делать? Постоянно перестраивать путь – накладно, много лишних вычислительных расходов, когда достаточно слегка изменить направление уже во время движения, чтобы избежать столкновения.
Виды изменения направления по ходу движения и есть steering behaviors.
Данная заметка — является переводом первой статьи из цикла Understanding Steering Behaviors, написанного Fernando Bevilacqua.
В русском языке оказалось сложно подобрать адекватный перевод я решил использовать термин «стиринг», который встречал на просторах рунета чаще всего. Стиринг помогает персонажам двигаться в реалистичной манере, с использованием простых сил, объединение которых позволяет добиться очень натурального перемещения персонажей по окружающему их миру. Идеи, лежащие в основе стиринга, были предложены Крейгом Рейнольдсом. В них не используются сложные стратегии, связанные с планированием пути или огромные вычисления, вместо этого используется доступная информация, например, силы, действующие на соседних персонажей (юнитов). Это делает их простыми для понимания и реализации, при этом, позволяя очень сложные паттерны перемещения.
Для понимания данной статьи следует иметь общее представление о математике векторов. Для тех кто хочет освежить знания в памяти, рекомендую ознакомиться со следующей статьей (Линейная алгебра для разработчиков игр).
Реализовать все силы, участвующие в изменении направления по ходу движения можно при помощи математических векторов. Так как эти силы будут влиять на скорость и положение персонажа, использование векторов — это хороший подход.
Хотя вектор должен иметь направление, оно будет игнорироваться, когда мы говорим про вектор положения персонажа (будем предполагать, что радиус-вектор направлен к текущему местоположению персонажа).

На рисунке выше изображён персонаж – его координаты (x,y); V(a, b) – вектор скорости. Движение рассчитывается по методу Эйлера.
Направление вектора скорости, будет контролировать куда персонаж направляется, в то время как длина вектора показывает как далека переместится персонаж за единицу времени. Чем больше длина вектора, тем быстрее будет перемещаться персонаж. Как правило вектор скорости может быть ограничен каким-либо значением, как правило используется максимальная скорость в моделируемом мире.
Скорость рассчитывается следующим образом:
где target – цель к которой мы движемся, position – текущее положение персонажа, max_velocity – максимальная скорость
Следует отметить, что без стиринга, персонаж движется только по прямой и, если меняется цель — изменяет свое направление мгновенно. Смотрятся такие перемещения очень неестественно.
Одной из идей стиринга является влияние на движение персонажа, посредством добавления управляющих сил (steering forces). В зависимости от них, персонаж будет двигаться в ту или иную сторону.
Для поведения Стремление (seek bahavior) добавление управляющей силы к персонажу, заставляет его плавно регулировать свою скорость, избегая резких изменений маршрута. Если цель переместится, то персонаж будет постепенно изменять свой вектор скорости, пытаясь достигнуть цели в его новом местоположении.
Поведение Стремление использует две силы: желаемую скорость (desired velosity) и управляющую силу (steering force):

Желаемая скорость — это сила, которая направляет персонажа к своей цели по кратчайшему возможному пути. Управляющая сила является результатом вычитания текущей скорости из желаемой и толкает персонаже в направлении цели. Эти силы рассчитываются следующим образом (следует помнить, что все операции производятся над векторами):
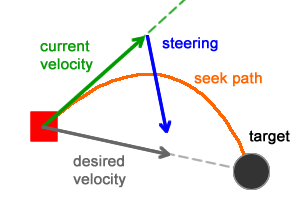
После того, как вычислен вектор управляющей силы, он должен быть добавлен к персонажу (к вектору скорости). Добавление управляющей силы каждый момент времени позволит персонажу отказаться от прямого маршрута и направиться к цели по плавной линии (оранжевая кривая на рисунке ниже).
Добавление этих сил и окончательный расчёт скорости и местоположения выглядят следующим образом:
Управляющая сила не может превышать максимально разрешенную силу, которая может действовать на персонажа. Также управляющую силу необходимо поделить на массу персонажа, что позволит рассчитать различные скорости движения в зависимости от веса персонажа.
Поведение Избегание (flee behavior) использует те же самые силы, что и в Стремлении (Seek Behavior), но они позволяют персонажу перемещаться прочь от цели.
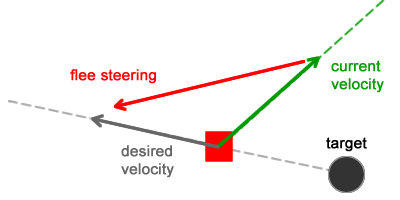
Новый вектор желаемой скорости рассчитывается путем вычитания положения персонажа из положения цели. В результате получается вектор который идет от цели к персонажу. Управляющая сила рассчитывается практически аналогично:
Желаемая скорость в этом случае представляет собой простейший маршрут, который персонаж может использовать, чтобы убежать от цели. Управляющая сила позволяет персонажу отказаться от текущего маршрута, толкая его в направлении желаемого вектора скорости.
Таким образом между итоговыми векторами в поведении Стремления и Избегания можно установить следующее соответствие:
Другими словами вектора противоположны друг другу по направлению.
После того как рассчитан вектор управляющей силы, он должен быть добавлен к вектору скорости персонажа. Таким образом эта сила толкает персонаж от цели, и в каждый момент времени персонаж перестает двигаться к цели и начать двигаться от нее (оранжевая кривая на рисунке ниже)

Стиринг является хорошим средством для создания реалистичных моделей движения. Несмотря на то, что расчёт прост в реализации, метод показывает очень хорошие результаты на практике.
Виды изменения направления по ходу движения и есть steering behaviors.
Данная заметка — является переводом первой статьи из цикла Understanding Steering Behaviors, написанного Fernando Bevilacqua.
В русском языке оказалось сложно подобрать адекватный перевод я решил использовать термин «стиринг», который встречал на просторах рунета чаще всего. Стиринг помогает персонажам двигаться в реалистичной манере, с использованием простых сил, объединение которых позволяет добиться очень натурального перемещения персонажей по окружающему их миру. Идеи, лежащие в основе стиринга, были предложены Крейгом Рейнольдсом. В них не используются сложные стратегии, связанные с планированием пути или огромные вычисления, вместо этого используется доступная информация, например, силы, действующие на соседних персонажей (юнитов). Это делает их простыми для понимания и реализации, при этом, позволяя очень сложные паттерны перемещения.
Для понимания данной статьи следует иметь общее представление о математике векторов. Для тех кто хочет освежить знания в памяти, рекомендую ознакомиться со следующей статьей (Линейная алгебра для разработчиков игр).
Позиция, Скорость и Движение
Реализовать все силы, участвующие в изменении направления по ходу движения можно при помощи математических векторов. Так как эти силы будут влиять на скорость и положение персонажа, использование векторов — это хороший подход.
Хотя вектор должен иметь направление, оно будет игнорироваться, когда мы говорим про вектор положения персонажа (будем предполагать, что радиус-вектор направлен к текущему местоположению персонажа).

На рисунке выше изображён персонаж – его координаты (x,y); V(a, b) – вектор скорости. Движение рассчитывается по методу Эйлера.
position = position + velocity
Направление вектора скорости, будет контролировать куда персонаж направляется, в то время как длина вектора показывает как далека переместится персонаж за единицу времени. Чем больше длина вектора, тем быстрее будет перемещаться персонаж. Как правило вектор скорости может быть ограничен каким-либо значением, как правило используется максимальная скорость в моделируемом мире.
Скорость рассчитывается следующим образом:
velocity = normalize(target - position) * max_velocity,
где target – цель к которой мы движемся, position – текущее положение персонажа, max_velocity – максимальная скорость
Следует отметить, что без стиринга, персонаж движется только по прямой и, если меняется цель — изменяет свое направление мгновенно. Смотрятся такие перемещения очень неестественно.
Расчёт сил
Одной из идей стиринга является влияние на движение персонажа, посредством добавления управляющих сил (steering forces). В зависимости от них, персонаж будет двигаться в ту или иную сторону.
Для поведения Стремление (seek bahavior) добавление управляющей силы к персонажу, заставляет его плавно регулировать свою скорость, избегая резких изменений маршрута. Если цель переместится, то персонаж будет постепенно изменять свой вектор скорости, пытаясь достигнуть цели в его новом местоположении.
Поведение Стремление использует две силы: желаемую скорость (desired velosity) и управляющую силу (steering force):
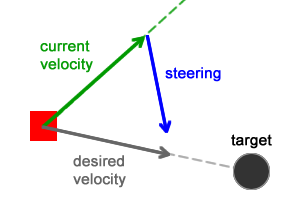
Желаемая скорость — это сила, которая направляет персонажа к своей цели по кратчайшему возможному пути. Управляющая сила является результатом вычитания текущей скорости из желаемой и толкает персонаже в направлении цели. Эти силы рассчитываются следующим образом (следует помнить, что все операции производятся над векторами):
desired_velocity = normalize(target - position) * max_velocity
steering = desired_velocity – velocity
Добавление сил
После того, как вычислен вектор управляющей силы, он должен быть добавлен к персонажу (к вектору скорости). Добавление управляющей силы каждый момент времени позволит персонажу отказаться от прямого маршрута и направиться к цели по плавной линии (оранжевая кривая на рисунке ниже).
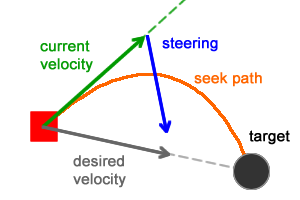
Добавление этих сил и окончательный расчёт скорости и местоположения выглядят следующим образом:
steering = truncate (steering, max_force)
steering = steering / mass
velocity = truncate (velocity + steering , max_speed)
position = position + velocity
Управляющая сила не может превышать максимально разрешенную силу, которая может действовать на персонажа. Также управляющую силу необходимо поделить на массу персонажа, что позволит рассчитать различные скорости движения в зависимости от веса персонажа.
Убегаем прочь
Поведение Избегание (flee behavior) использует те же самые силы, что и в Стремлении (Seek Behavior), но они позволяют персонажу перемещаться прочь от цели.
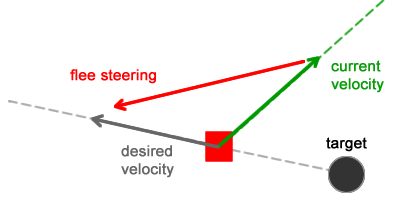
Новый вектор желаемой скорости рассчитывается путем вычитания положения персонажа из положения цели. В результате получается вектор который идет от цели к персонажу. Управляющая сила рассчитывается практически аналогично:
desired_velocity = normalize(position - target) * max_velocity
steering = desired_velocity – velocity
Желаемая скорость в этом случае представляет собой простейший маршрут, который персонаж может использовать, чтобы убежать от цели. Управляющая сила позволяет персонажу отказаться от текущего маршрута, толкая его в направлении желаемого вектора скорости.
Таким образом между итоговыми векторами в поведении Стремления и Избегания можно установить следующее соответствие:
flee_desired_velocity = -seek_desired_velocity
Другими словами вектора противоположны друг другу по направлению.
После того как рассчитан вектор управляющей силы, он должен быть добавлен к вектору скорости персонажа. Таким образом эта сила толкает персонаж от цели, и в каждый момент времени персонаж перестает двигаться к цели и начать двигаться от нее (оранжевая кривая на рисунке ниже)

Заключение
Стиринг является хорошим средством для создания реалистичных моделей движения. Несмотря на то, что расчёт прост в реализации, метод показывает очень хорошие результаты на практике.