
Доброго времени суток, уважаемое хабрасообщество.
Сегодня я хотел бы затронуть такую увлекательную тему, как математические парадоксы. По данной теме на хабре уже было опубликовано несколько замечательных статей (1,2,3,4,5), но в математике интересные парадоксы этой выборкой далеко не исчерпываются.
Поэтому попробуем рассмотреть другие занимательные парадоксы (а некоторые и «не совсем» парадоксы), которые пока еще не получили здесь должного освещения.
Парадокс кучи и парадокс «Лысого»
Данные парадоксы известны еще с древности. Для начала сформулируем и рассмотрим парадокс кучи, связанного с неопределенностью понятия «куча»:

«если к одному зерну добавлять по зёрнышку, то в какой момент образуется куча?»
или обратная формулировка:
«удаляя из кучи в 1 млн зёрен по одному зёрнышку, с какого момента она перестаёт быть кучей?»
Формулировка парадокса основана на очевидной предпосылке, согласно которой одно зёрнышко не образует кучи, и индуктивной предпосылке, по которой добавление одного зернышка к совокупности, кучей не являющейся, несущественно для образования кучи. Из этих предпосылок следует, что никакая совокупность из сколь угодно большого количества зёрен не будет образовывать кучи, что противоречит представлению о существовании кучи из зёрен. Очевидно, что эти рассуждения приводят к неправильным выводам.
Однако до самого недавнего времени не было ясно, какие тогда рассуждения здесь использовать. Лишь с появлением теории нечетких множеств Лофти Заде и нечеткой логики стало ясно, что здесь уместны нечеткие расуждения, поскольку имеется в наличии классический объект нечеткой логики — неопределенное понятие «быть кучей». Данные объекты в нечеткой логике интерпретируются как имеющие неточное значение, характеризуемое некоторым нечётким множеством.
Согласно таким рассуждениям заключение на каждом шаге остается прежним, но принадлежность его правильности уменьшается с каждым шагом. Когда эта принадлежность падает меньше 50%, то более правильным становится противоположное заключение.
Аналогичные рассуждения можно применить и к парадоксу «Лысого»:
«Если волосы с головы выпадают по одному, с какого момента человек становится лысым?»
Парадокс лжеца

Если утверждение на картинке истинно, значит, исходя из его содержания, верно то, что оно — ложно; но если оно — ложно, тогда то, что оно утверждает, неверно; значит, неверно, что утверждение на картинке — ложно, и, значит, это утверждение истинно.
Парадокс лжеца демонстрирует расхождение разговорной речи с формальной логикой, вводя высказывание, которое одновременно и истинно и ложно. В рамках формальной логики данное утверждение не доказуемо и неопровержимо, поэтому решения данного парадокса не существует, но существуют различные варианты его устранения.
Для этого можно применить рассуждения используемые в предыдущем разделе, для этого положим, что утверждение истинно на 0,5, тогда оно и ложно на 0,5, то есть не всякую фразу можно назвать целиком ложной или целиком истинной — «в чем-то высказывание на картинке лжет, а в чем-то — говорит правду»
К такому же выводу можно придти с помощью тройственной логики. В ней есть три степени истинности: «истина», «ложь» и «неопределенно». Под «неопределенно» понимается промежуточное по смыслу значение между истиной и ложью. К данной степени истинности и относят парадокс лжеца.
Как уже говорилось это не решения парадокса лжеца, а всего лишь объяснения, почему данный парадокс возникает в классической двузначной логике высказываний. Они свидетельствует, что строгое деление всех высказываний на истинные и ложные в данном случае неприменимо, поскольку ведет к парадоксу.
В настоящее всемя многие придерживаются такой точки зрения, что данное высказывание вообще не является логическим утверждением, и применять к нему классические методы формальной логики бессмысленно.
Парадокс Тесея
Данный парадокс можно сформулировать следующим образом:

«Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?»
Было предложено несколько решений этого парадокса. Согласно философской школе Аристотеля существует несколько описывающих объект причин: форма, материал и суть вещи (которая, по учению Аристотеля, является самой важной характеристикой). Исходя из этого корабль остался тем же, так как его суть не поменялась, лишь изменился износившийся материал.
В следующем решении предложили дать аргументу «тот же» количественную и качественную характеристику. В таком случае, после смены досок корабль Тесея окажется количественно тем же, а качественно — уже другим кораблём.
В последнее время для решения парадокса Тесея предложили использовать 4-х мерную интерпретацию, в которой 3-х мерный корабль имеет также протяженность в 4 измерении-времени. Получившийся 4-х мерный корабль на протяжении временного ряда количественно идентичен с собой. Но отдельные «временные срезы» качественно могут отличаться друг от друга.
Парадокс Абилина

Данный парадокс заключается в том, что группа людей может принять решение, противоречащее возможному выбору любого из членов группы из-за того, что каждый индивидуум считает, что его цели противоречат целям группы, а потому не возражает.
Парадокс был описан Джерри Харви в статье The Abilene Paradox and other Meditations on Management. Имя парадоксу дано по мотивам следующего анекдота, описанного в этой статье:
В один жаркий техасский вечер некая семья играла в домино на крыльце до тех пор, пока тесть не предложил съездить в Абилин отобедать. Жена сказала: «Звучит неплохо». Муж, несмотря на то, что поездка обещала быть долгой и жаркой, подумал, что надо бы подстроиться под других, и произнёс: «По-моему, неплохо; надеюсь, что и твоя мама не откажется». Тёща же ответила: «Конечно, поехали! Я не была в Абилине уже давно».
Дорога была жаркой, пыльной и долгой. Когда же они наконец приехали в кафетерий, еда оказалась невкусной. Спустя четыре часа они, измученные, вернулись домой.
Один из них произнёс неискренне: «Верно, неплохая была поездка?». Тёща на это сказала, что, на самом деле, она бы лучше осталась бы дома, но поехала, раз уж остальные трое были полны энтузиазма. Муж сказал: «Я был бы рад никуда не ездить, поехал лишь чтобы доставить остальным удовольствие». Жена произнесла: «А я поехала, рассчитывая на радость остальных. Надо было быть сумасшедшим, чтобы добровольно отправиться в эту поездку». Тесть ответил, что он предложил это лишь потому, что ему показалось, что остальным скучно.
И они сидели, ошеломлённые тем, что поехали в поездку, которой никто из них не хотел. Каждый из них предпочёл бы спокойно наслаждаться тем днём.
Данный парадокс легко объясняется различными социологическими науками, подтверждающими, что человек редко совершает поступки, противоречащие поступкам его группы. Думаю многие не раз сталкивались с данном парадоксом и в своей жизни.
Парадокс Симпсона и феномен Уилла Роджерса
Замечу, что данные парадоксы являются «кажущимися», то есть они могут возникнуть на интуитивном уровне, но если провести вычисления, то легко убедиться, что никакого парадокса не возникает.
Для иллюстрации парадокса Симпсона рассмотрим пример, описанный известным популяризатором математики Мартином Гарднером.
Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень набора № 1 выше, чем из набора № 2. В свою очередь, вероятность вытащить чёрный камень из набора № 3 больше, чем из набора № 4. Объединим набор № 1 с набором № 3 (получим набор I), а набор № 2 — с набором № 4 (набор II). Интуитивно можно ожидать, что вероятность вытащить чёрный камень из набора I будет выше, чем из набора II. Однако, в общем случае такое утверждение неверно.
Пример, в котором выполняется парадокс Симпсона:
| Черные шары | Белые шары | Вероятность вытащить черный камень | |
|---|---|---|---|
| Набор №1 | 6 | 7 | 6/13 ≈ 0,4615 |
| Набор №2 | 4 | 5 | 4/9 ≈ 0,4444 |
| Набор №3 | 6 | 3 | 6/9 ≈ 0,6667 |
| Набор №4 | 9 | 5 | 9/14 ≈ 0,6429 |
Теперь смешаем наборы №1 и №3 — из которых черные камни можно вытащить с большей вероятностью и наборы №2 и №4 — из которых черные камни можно вытащить с меньшей вероятностью.
| Черные шары | Белые шары | Вероятность вытащить черный камень | |
|---|---|---|---|
| Набор I | 12 | 10 | 12/22 ≈ 0,5454 |
| Набор II | 13 | 10 | 13/23 ≈ 0,5652 |
Как мы видим из таблицы после смешивания вероятность вытащить черный камень из набора II стала выше чем из набора I.
Математически никакого парадокса тут нет, так как общая вероятность набора зависит от соотношения количества камней черного цвета и обоих цветов, в данном случае в 4 наборе было 9 черных камней, а в первом аж 7 белых, которые больше всего и повлияли на итоговый расклад.
Близок к парадоксу Симпсона и феномен Уилла Роджерса. По сути в них описывается одно и то же явление, но в других терминах.
Думаю многие не раз сталкивались с фразами подобные такой:
«Когда оки покинули Оклахому и переехали в Калифорнию, то повысили средний интеллект обоих штатов»
Эту фразу приписывают Уиллу Роджерсу, в честь чего феномен и получил свое название.
С точки зрения математики никакого парадокса тут тоже нет. Чтобы в этом убедиться достаточно рассмотреть два множества: первое — {1, 2}, а второе — {90,100}, если число 90 из второго множества перенести в первое, то среднее арифметическое элементов как первого множества так и второго повысится.
Исчезновение клетки
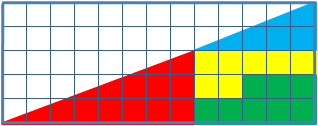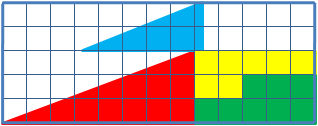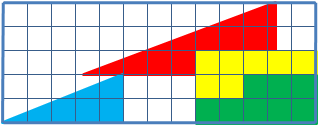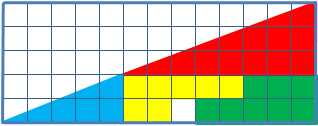
Широкий класс задач на перестановку фигур, обладающих признаками софизмов: изначально в их условие введена замаскированная ошибка. В какой-то мере данные задачи ближе к оптическим иллюзиям, чем к математике.
Для примера расмотрим одну подобную задачу: дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка.
Математически парадоксов и таинственного исчезновения площади тут нет. Визуально наблюдаемые треугольники, на самом деле таковымы не являются, гипотенузы в обоих псевдотреугольниках на самом деле являются ломаными линиями (в первом треугольнике она с изломом внутрь, а во втором — наружу). Если наложить треугольник друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «пропавшая» площадь.
Вместо заключения
К моему большому сожалению невозможно рассмотреть все интересные математические парадоксы (и «не совсем» парадоксы) в рамках одной статьи. Но надеюсь, что данная статья не оставила Вас равнодушными, и буду очень рад если Вы решите, что не зря потратили время за чтением.