В этой статье пойдёт речь о том, как реализован словарь в Python. Я постараюсь ответить на вопрос, почему элементы словаря не упорядочены, описать, каким образом словари хранят, добавляют и удаляют свои элементы. Надеюсь, что статья будет полезна не только людям, изучающим Python, но и всем, кто интересуется внутренним устройством и организацией структур данных.
На написание этой статьи меня натолкнул вопрос на Stack Overflow.
В статье рассматривается реализация CPython версии 2.7. Все примеры были подготовлены в 32-битной версии Python на 64-битной ОС, для другой версии значения будут отличаться.
Словарь в Python является ассоциативным массивом, то есть хранит данные в виде пар (ключ, значение). Словарь – измененяемый тип данных. Это значит, что в него можно добавлять элементы, изменять их и удалять из словаря. Он также предоставляет операцию поиска и возвращения элемента по ключу.
Инициализация и добавление элементов:
Получение элемента:
Удаление элемента:
Ключами словаря могут быть значения только hashable типов, то есть типов, у которых может быть получен хэш (для этого у них должен быть метод __hash__()). Поэтому значения таких типов, как список (list), набор (set) и собственно сам словарь (dict), не могут быть ключами словаря:
Словарь в Python реализован в виде хэш-таблицы. Как известно, реализация хэш-таблицы должна учитывать возможность появления коллизий – ситуаций, когда разные ключи имеют одинаковое значение хэша. Должен быть способ вставки и извлечения элементов с учётом коллизий. Существует несколько способов разрешения коллизий, например метод цепочек и метод открытой адресации. В Python используется метод открытой адресации. Разработчики предпочли метод открытой адресации методу цепочек ввиду того, что он позволяет значительно сэкономить память на хранении указателей, которые используются в хэш-таблицах с цепочками.
В рассматриваемой реализации каждая запись (PyDictEntry) в хэш-таблице словаря состоит из трёх элементов – хэш, ключ и значение.
Структура PyDictObject выглядит следующим образом:
При создании нового объекта словаря его размер равен 8. Это значение определяется константой PyDict_MINSIZE. Для хранения хэш-таблицы в PyDictObject были введены переменные ma_smalltable и ma_table. Переменная ma_smalltable с предвыделенной памятью размером PyDict_MINSIZE (то есть 8) позволяет небольшим словарям (до 8 объектов PyDictEntry) храниться без дополнительного выделения памяти. Эксперименты, проведённые разработчиками, показали, что этого размера вполне достаточно для большинства словарей: небольших словарей экземпляров и обычно небольших словарей, созданных для передачи именованных аргументов (kwargs). Переменная ma_table соответствует ma_smalltable для маленьких таблиц (то есть для таблиц из 8 ячеек). Для таблиц большего размера память ma_table выделяется отдельно. Переменная ma_table не может быть равна NULL.
Если кому-то вдруг захочется изменить значение PyDict_MINSIZE, это можно сделать в исходниках, а затем пересобрать Python. Значение рекомендуется делать равным степени двойки, но не меньше четырёх.
1) Неиспользованная (me_key == me_value == NULL)
Данное состояние означает, что ячейка не содержит и ещё никогда не содержала пару (ключ, значение).
После вставки ключа «неиспользованная» ячейка переходит в состояние «активная».
Это состояние – единственный случай, когда me_key = NULL и является начальным состоянием для всех ячеек в таблице.
2) Активная (me_key != NULL и me_key != dummy и me_value != NULL)
Означает, что ячейка содержит активную пару (ключ, значение).
После удаления ключа ячейка из состояния «активная» переходит в состояние «пустая» (то есть me_key = dummy, а
dummy = PyString_FromString("<dummy key>")).
Это единственное состояние, когда me_value != NULL.
3) Пустая (me_key == dummy и me_value == NULL)
Это состояние говорит о том, что ячейка ранее содержала активную пару (ключ, значение), но она была удалена, и новая активная пара ещё не записана в ячейку.
Так же как и при состоянии «неиспользованная», после вставки ключа ячейка из состояния «пустая» переходит в состояние «активная».
«Пустая» ячейка не может вернуться в состояние «неиспользованная», то есть вернуть me_key = NULL, так как в данном случае последовательность проб в случае коллизии не будет иметь возможность узнать, были ли ячейки «активны».
ma_fill – число ненулевых ключей (me_key != NULL), то есть сумма «активных» и «пустых» ячеек.
ma_used – число ненулевых и не «пустых» ключей (me_key != NULL, me_key != dummy), то есть число «активных» ячеек.
ma_mask – маска, равная PyDict_MINSIZE — 1.
ma_lookup – функция поиска. По умолчанию при создании нового словаря используется lookdict_string. Так сделано потому, что разработчики посчитали, что большинство словарей содержат только строковые ключи.
Эффективность хэш-таблицы зависит от наличия «хороших» хэш-функций. «Хорошая» хэш-функция должна вычисляться быстро и с минимальным количеством коллизий. Но, к сожалению, наиболее часто используемые и важные хэш-функции (для строкового и целого типов) возвращают достаточно регулярные значения, что приводит к коллизиям. Возьмём пример:
Для целых чисел хэшами являются их значения, поэтому подряд идущие числа будут иметь подряд идущие хэши, а для строк подряд идущие строки имеют практически подряд идущие хэши. Это не обязательно плохо, напротив, в таблице размером 2**i взятие i младших бит хэша как начального индекса таблицы выполняется очень быстро, и для словарей, проиндексированных последовательностью целых чисел, коллизий не будет вообще:
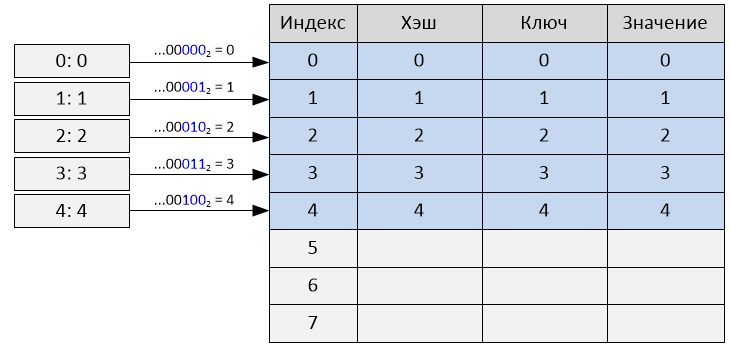
То же самое будет почти полностью соблюдаться, если ключи словаря – это «подряд идущие» строки (как в примере выше). В общих случаях это дает более чем случайное поведение, что и требуется.
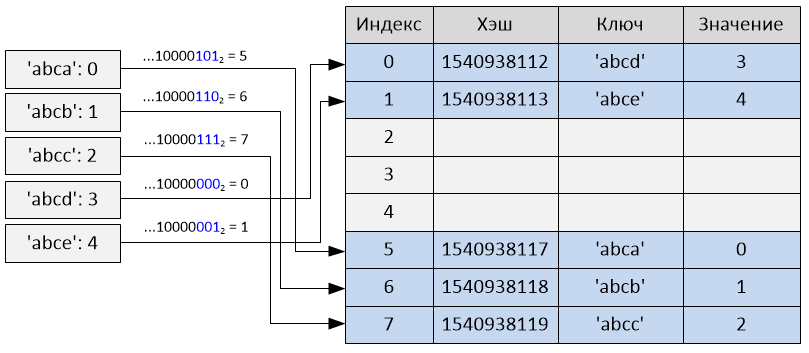
Взятие только i младших бит хэша в качестве индекса также уязвимо к коллизиям: например, возьмём список [i << 16 for i in range(20000)] в качестве набора ключей. Так как целые являются их собственными хэшами и это вписывается в словарь размера 2**15 (так как 20000 < 32768), последние 15 бит от каждого хэша все будут равны 0.
Получится, что все ключи будут иметь один и тот же индекс. То есть для всех ключей (кроме первого) произойдут коллизии.
Примеры специально подобранных «плохих» случаев не должны влиять на обычные случаи, так что просто оставим взятие последних i бит. Всё остальное отдаётся на откуп методу разрешения коллизий.
Процедура выбора подходящей ячейки для вставки элемента в хэш-таблицу называется пробирование, а рассматриваемая ячейка-кандидат – проба.
Обычно ячейка находится с первой попытки (и это действительно так, ведь коэффициент заполнения хэш-таблицы держится ниже 2/3), что позволяет не тратить время на пробирование и делает расчет начального индекса очень быстрым. Но давайте рассмотрим, что случится, если произойдёт коллизия.
Первая часть метода разрешения коллизий заключается в расчёте индексов таблицы для пробирования с помощью формулы:
Для любого начального j в пределах [0..(2**i — 1)] вызов данной формулы 2**i раз вернёт каждое число в пределах [0..(2**i — 1)] ровно один раз. Например:
Вы скажете, что это ничем не лучше использования линейного пробирования с постоянным шагом, ведь в данном случае ячейки в хэш-таблице также просматриваются в определенном порядке, но это не единственное отличие. В общих случаях, когда хэш значения ключей идут подряд, данный метод лучше линейного пробирования. Из примера выше можно проследить, что для таблицы размером 8 (2**3) порядок индексов будет следующим:
Если произойдёт коллизия для пробы с индексом, равным 5, то следующий индекс пробы будет 2, а не 6, как в случае линейного пробирования с шагом +1, поэтому для ключа, добавляемого в будущем, индекс пробы которого будет равен 6, коллизии не произойдёт. Линейное пробирование в данном случае (при последовательных значениях ключей) было бы плохим вариантом, так как происходило бы много коллизий. Вероятность же того, что хэш значения ключей будут идти в порядке 5 * j + 1, намного меньше.
Вторая часть метода разрешения коллизий заключается в использовании не только младших i бит хэша, но и остальных бит тоже. Это реализовано с использованием переменной perturb следующим образом:
После этого последовательность проб будет зависеть от каждого бита хэша. Псевдослучайное изменение очень эффективно, потому что быстро увеличивает различия в битах. Так как переменная perturb – беззнаковая, то, если пробирование выполняется достаточно часто, переменная perturb в конечном итоге становится и остаётся равной нулю. В этот момент (который достигается очень редко) результат j снова становится равен 5 * j + 1. Далее поиск происходит точно так же, как в первой части метода, и свободная ячейка в конечном счете будет найдена, поскольку, как было сказано ранее, каждое число в диапазоне [0..(2**i — 1)] будет возвращено ровно один раз, и мы уверены, что всегда есть по крайней мере одна «неиспользованная» ячейка.
Выбор «хорошего» значения для PERTURB_SHIFT – это вопрос балансировки. Если сделать его малым, то старшие биты хэша будут влиять на последовательность проб по итерациям. Если же сделать его большим, то в действительно «плохих» случаях старшие биты хэша будут оказывать влияние только на ранних итерациях. В результате экспериментов, которые провёл один из разработчиков Python – Тим Питерс, значение PERTURB_SHIFT было выбрано равным 5, так как это значение оказалось «лучшим». То есть показало минимальное общее число коллизий как для нормальных, так и для специально подобранных «плохих» случаев, хотя значения 4 и 6 не были значительно хуже.
Историческая справка: Один из разработчиков Python, Реймер Берендс, предлагал идею использования подхода расчёта индексов таблицы, основанного на многочленах, который затем был улучшен Кристианом Тисмером. Этот подход также показал отличные результаты по возникновению коллизий, но требовал больше операций, а также дополнительной переменной для хранения многочлена таблицы в структуре PyDictObject. В экспериментах Тима Питерса текущий, используемый в Python метод оказался быстрее, показывая в равной степени хорошие результаты по возникновению коллизий, но требовал меньше кода и использовал меньше памяти.
Когда вы создаёте словарь, вызывается функция PyDict_New. В этой функции последовательно выполняются следующие операции: происходит выделение памяти для нового объекта словаря PyDictObject. Переменная ma_smalltable очищается. Переменные ma_used и ma_fill приравниваются 0, ma_table становится равной ma_smalltable. Значение ma_mask приравнивается PyDict_MINSIZE — 1. Функция для поиска ma_lookup делается равной lookdict_string. Возвращается созданный объект словаря.
При добавлении элемента в словарь или изменении значения элемента в словаре вызывается функция PyDict_SetItem. В этой функции берётся значение хэша и вызывается функция insertdict, а также функция dictresize, если таблица заполняется на 2/3 от текущего размера.
В свою очередь в функции insertdict происходит вызов lookdict_string (или lookdict, если в словаре есть не строковый ключ), в которой происходит поиск свободной ячейки в хэш-таблице для вставки. Эта же функция используется для нахождения ключа при извлечении.
Начальный индекс пробы в этой функции рассчитывается как хэш ключа, поделённый по модулю на размер таблицы (таким образом, происходит взятие младших бит хэша). То есть:
В Python это реализовано с использованием логической операции «И» и маски. Маска равна следующему значению: mask = PyDict_MINSIZE — 1.
Так получаются младшие биты хэша:
2**i = PyDict_MINSIZE, отсюда i = 3, то есть достаточно трёх младших бит.
hash(123) = 123 = 11110112
mask = PyDict_MINSIZE — 1 = 8 — 1 = 7 = 1112
index = hash(123) & mask = 11110112 & 1112 = 0112 = 3
После того как индекс рассчитан, выполняется проверка ячейки по индексу, и если она «неиспользованная», то в неё добавляется запись (хэш, ключ, значение). Но если эта ячейка занята, из-за того, что другая запись имеет тот же хэш (то есть произошла коллизия), выполняется сравнение хэша и ключа вставляемой записи и записи в ячейке. Если хэш и ключ для записей совпадают, то считается, что запись уже существует в словаре, и выполняется её обновление.
Это объясняет хитрый момент, связанный с добавлением равных по значению, но разных по типу ключей (к примеру, float, int и complex):
То есть тот тип, который был добавлен в словарь первым, и будет типом ключа, несмотря на обновление. Это объясняется тем, что реализация хэша для float значений возвращает хэш от int, если дробная часть равна 0.0. Пример расчёта хэша для float, переписанный на Python:
А хэш от complex возвращает хэш от float. В данном случае возвращается хэш только действительной части, так как мнимая часть равна нулю:
Пример:
Ввиду того, что и хэши, и значения для всех трёх типов равны, выполняется простое обновление значения найденной записи.
Замечание по поводу добавления элементов: Python запрещает добавление элементов в словарь во время итерации, поэтому при попытке добавить новый элемент произойдёт ошибка:
Вернёмся к процедуре добавления элемента в словарь. После успешного добавления или обновления записи в хэш-таблице происходит сравнение следующей записи-кандидата на вставку. Если хэш или ключ у записей не совпадают, начинается пробирование. Происходит поиск «неиспользованной» ячейки для вставки. В данной реализации Python используется случайное (а если переменная perturb равна нулю – квадратичное) пробирование. Как было описано выше, при случайном пробировании индекс следующей ячейки выбирается псевдослучайным образом. Запись добавляется в первую найденную «неиспользованную» ячейку. То есть два ключа a и b, у которых hash(a) == hash(b), но a != b могут легко существовать в одном словаре. В случае если ячейка по начальному индексу пробы «пустая», произойдёт пробирование. И если первая найденная ячейка будет «нулевая», то «пустая» ячейка будет использована заново. Это позволяет перезаписать удалённые ячейки, сохраняя ещё неиспользованные.
Получается, что индексы добавляемых в словарь элементов зависят от уже находящихся в нём элементов, и порядок ключей для двух словарей, состоящих из одного и того же набора пар (ключ, значение), может быть разным и определяется очерёдностью добавления элементов:
Это объясняет, почему словари в Python при выводе содержимого отображают хранимые пары (ключ, значение) не в порядке их добавления в словарь. Словари выводят их в порядке расположения в хэш-таблице (то есть в порядке индексов).
Рассмотрим пример:
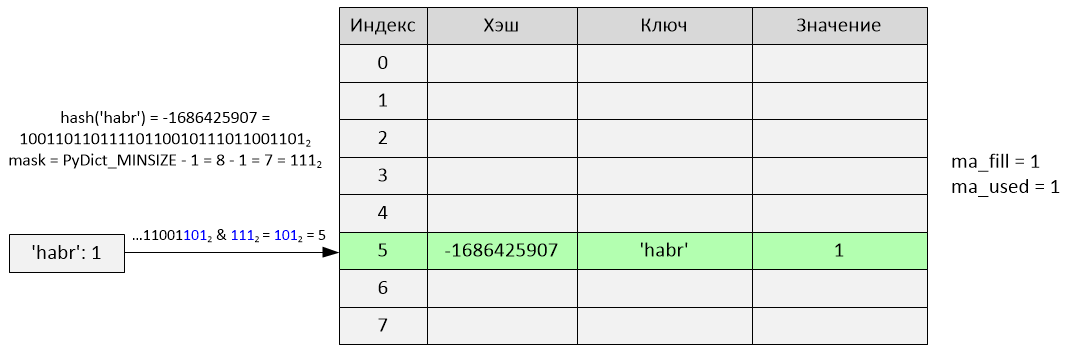
Произошла вставка по индексу 5. Переменные ma_fill и ma_used стали равны 1.
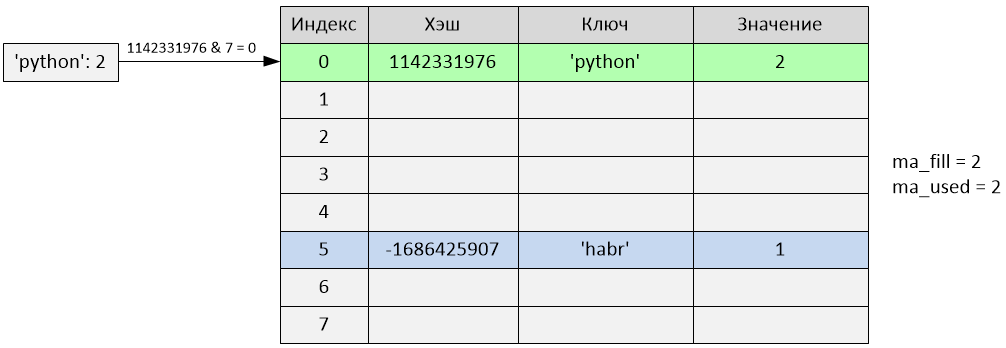
Произошла вставка по индексу 0. Переменные ma_fill и ma_used стали равны 2.
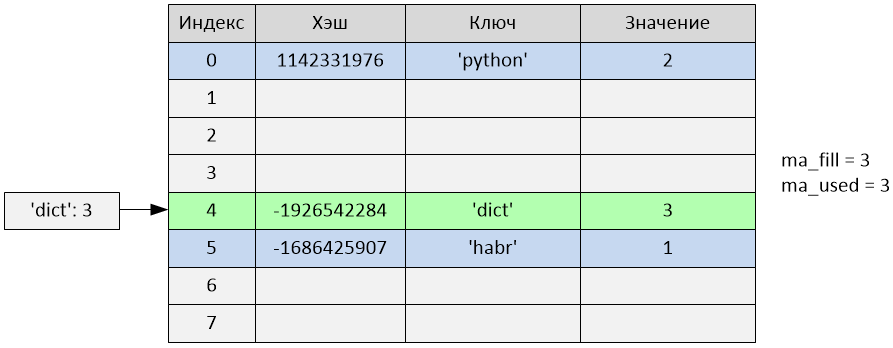
Произошла вставка по индексу 4. Переменные ma_fill и ma_used стали равны 3.
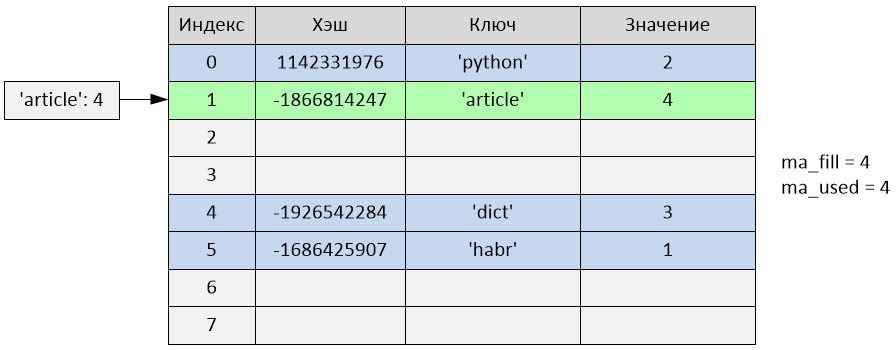
Произошла вставка по индексу 1. Переменные ma_fill и ma_used стали равны 4.
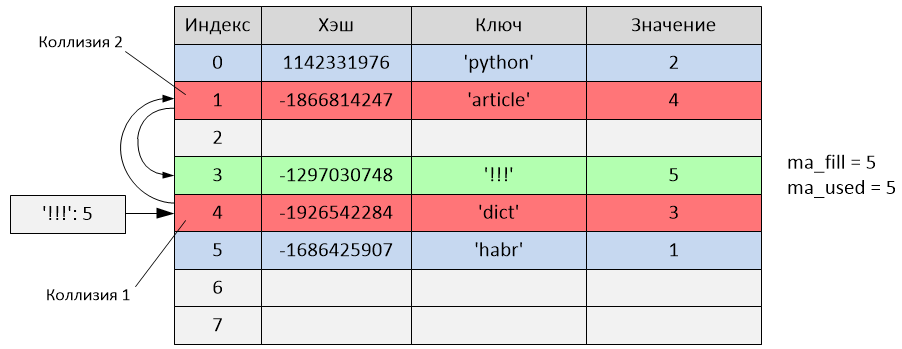
Произошло следующее:
hash('!!!') = -1297030748
i = -1297030748 & 7 = 4
Но как видно из таблицы, индекс 4 уже занят записью с ключом 'dict'. То есть произошла коллизия. Начинается пробирование:
perturb = -1297030748
i = (i * 5) + 1 + perturb
i = (4 * 5) + 1 + (-1297030748) = -1297030727
index = -1297030727 & 7 = 1
Новый индекс пробы равен 1, но данный индекс тоже занят (записью с ключом 'article'). Произошла ещё одна коллизия, продолжаем пробирование:
perturb = perturb >> PERTURB_SHIFT
perturb = -1297030748 >> 5 = -40532211
i = (i * 5) + 1 + perturb
i = (-1297030727 * 5) + 1 + (-40532211) = -6525685845
index = -6525685845 & 7 = 3
Новый индекс пробы равен 3, и, так как он не занят, происходит вставка записи с ключом '!!!' в ячейку с третьим индексом. В данном случае запись была добавлена после двух проб из-за произошедших коллизий. Переменные ma_fill и ma_used стали равны 5.
Пробуем добавить шестой элемент в словарь.
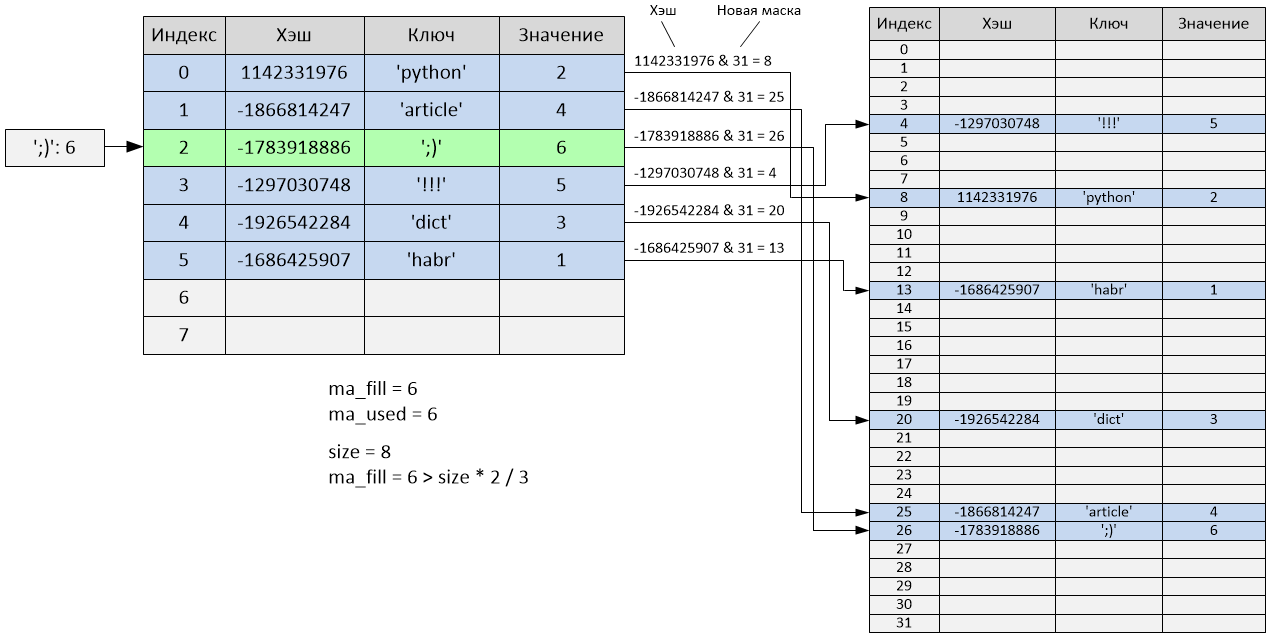
После добавления шестого элемента таблица будет заполнена на 2/3, а соответственно, произойдёт изменение её размера. После того как размер изменится (в данном случае увеличится в 4 раза), произойдёт полная перестройка хэш-таблицы с учётом нового размера – все «активные» ячейки будут перераспределены, а «пустые» и «неиспользованные» ячейки будут проигнорированы.
Размер хэш-таблицы теперь равен 32, а переменные ma_fill и ma_used стали равны 6. Как видно, порядок элементов полностью поменялся:
Поиск записи в хэш-таблице словаря происходит аналогично, начинаясь с ячейки i, где i зависит от хэша ключа. Если хэш и ключ не совпадают с хэшом и ключом найденной записи (то есть была коллизия и надо найти подходящую запись) – начинается пробирование, которое продолжается, пока не будет найдена запись, для которой хэш и ключ совпадают. Если же все ячейки были просмотрены, но запись не найдена, возвращается ошибка.
Размер таблицы изменяется, когда она заполняется на 2/3. То есть для начального размера хэш-таблицы словаря, равного 8, изменение произойдёт после того, как будет добавлен 6 элемент.
При этом происходит перестройка хэш-таблицы с учётом её нового размера, а соответственно, меняются и индексы всех записей.
Значение 2/3 от размера было выбрано как оптимальное, для того чтобы пробирование не занимало слишком много времени, то есть вставка новой записи происходила быстро. Увеличение этого значения приводит к тому, что словарь плотнее заполняется записями, что в свою очередь увеличивает количество коллизий. Уменьшение же увеличивает разреженность записей в ущерб увеличения занимаемых ими кэш-линий процессора и в ущерб увеличения общего объема памяти. Проверка заполнения таблицы происходит в весьма чувствительном ко времени участке кода. Попытки сделать проверку более сложной (например, изменяя коэффициент заполнения для разных размеров хэш-таблицы) уменьшали производительность.
Проверить, что размер словаря действительно изменяется, можно так:
В примере возвращается размер всего объекта PyDictObject для 64-битной версии ОС.
Начальный размер таблицы равен 8. Таким образом, когда число заполненных ячеек будет равно 6 (то есть больше 2/3 от размера), размер таблицы увеличится до 32. Затем, когда число будет равно 22, увеличится до 128. При 86 увеличится до 512, при 342 – до 2048 и так далее.
Коэффициент увеличения размера таблицы при достижении максимального уровня заполнения равен 4, если размер таблицы меньше 50000 элементов, и 2 – для таблиц большего размера. Такой подход может быть полезен приложениям с ограничениями по памяти.
Увеличение размера таблицы улучшает среднюю разреженность, то есть разбросанность записей по таблице словаря (уменьшая коллизии), за счёт увеличения объема потребляемой памяти и скорости итераций, а также уменьшает количество дорогостоящих операций выделения памяти при изменении размера для растущего словаря.
Обычно добавление элемента в словарь может увеличить его размер в 4 или 2 раза в зависимости от текущего размера словаря, но также возможно, что размер словаря уменьшится. Такая ситуация может произойти, если ma_fill (количество ненулевых ключей, сумма «активных» и «пустых» ячеек) намного больше ma_used (количество «активных» ячеек), то есть много ключей было удалено.
При удалении элемента из словаря вызывается функция PyDict_DelItem.
Удаление из словаря происходит по ключу, хотя в действительности освобождения памяти не происходит. В этой функции вычисляется хэш значение ключа, а затем происходит поиск записи в хэш-таблице с использованием всё той же функции lookdict_string или lookdict. В случае если запись с таким ключом и хэшем найдена, ключ этой записи выставляется в состояние «пустой» (то есть me_key = dummy), а значение записи – в NULL (me_value = NULL). После этого переменная ma_used уменьшится на единицу, а ma_fill останется без изменения. Если же запись не найдена, возвращается ошибка.
После удаления переменная ma_used стала равна 4, а ma_fill осталась равной 5, так как ячейка не была удалена, а всего лишь была помечена как «пустая» и продолжает занимать ячейку в хэш-таблице.
При запуске python можно воспользоваться ключом -R, чтобы использовать псевдослучайную «соль». В этом случае хэш значения таких типов, как строки, buffer, bytes, и объекты datetime (date, time и datetime) будут непредсказуемыми между вызовами интерпретатора. Данный способ предложен в качестве защиты от DoS атак.
github.com/python/cpython/blob/2.7/Objects/dictobject.c
github.com/python/cpython/blob/2.7/Include/dictobject.h
github.com/python/cpython/blob/2.7/Objects/dictnotes.txt
www.shutupandship.com/2012/02/how-hash-collisions-are-resolved-in.html
www.laurentluce.com/posts/python-dictionary-implementation
rhodesmill.org/brandon/slides/2010-03-pycon
www.slideshare.net/MinskPythonMeetup/ss-26224561 – Dictionary в Python. По мотивам Objects/dictnotes.txt – SlideShare (Cyril notorca Lashkevich)
www.youtube.com/watch?v=JhixzgVpmdM – Видео доклада «Dictionary в Python. По мотивам Objects/dictnotes.txt»
На написание этой статьи меня натолкнул вопрос на Stack Overflow.
В статье рассматривается реализация CPython версии 2.7. Все примеры были подготовлены в 32-битной версии Python на 64-битной ОС, для другой версии значения будут отличаться.
Словарь в Python
Словарь в Python является ассоциативным массивом, то есть хранит данные в виде пар (ключ, значение). Словарь – измененяемый тип данных. Это значит, что в него можно добавлять элементы, изменять их и удалять из словаря. Он также предоставляет операцию поиска и возвращения элемента по ключу.
Инициализация и добавление элементов:
>>> d = {} # то же самое, что d = dict()
>>> d['a'] = 123
>>> d['b'] = 345
>>> d['c'] = 678
>>> d
{'a': 123, 'c': 678, 'b': 345}
Получение элемента:
>>> d['b']
345
Удаление элемента:
>>> del d['c']
>>> d
{'a': 123, 'b': 345}
Ключами словаря могут быть значения только hashable типов, то есть типов, у которых может быть получен хэш (для этого у них должен быть метод __hash__()). Поэтому значения таких типов, как список (list), набор (set) и собственно сам словарь (dict), не могут быть ключами словаря:
>>> d[list()] = 1
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'
>>> d[set()] = 2
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'set'
>>> d[dict()] = 3
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'dict'
Реализация
Словарь в Python реализован в виде хэш-таблицы. Как известно, реализация хэш-таблицы должна учитывать возможность появления коллизий – ситуаций, когда разные ключи имеют одинаковое значение хэша. Должен быть способ вставки и извлечения элементов с учётом коллизий. Существует несколько способов разрешения коллизий, например метод цепочек и метод открытой адресации. В Python используется метод открытой адресации. Разработчики предпочли метод открытой адресации методу цепочек ввиду того, что он позволяет значительно сэкономить память на хранении указателей, которые используются в хэш-таблицах с цепочками.
В рассматриваемой реализации каждая запись (PyDictEntry) в хэш-таблице словаря состоит из трёх элементов – хэш, ключ и значение.
typedef struct {
Py_ssize_t me_hash;
PyObject *me_key;
PyObject *me_value;
} PyDictEntry;
Структура PyDictObject выглядит следующим образом:
#define PyDict_MINSIZE 8
typedef struct _dictobject PyDictObject;
struct _dictobject {
PyObject_HEAD
Py_ssize_t ma_fill;
Py_ssize_t ma_used;
Py_ssize_t ma_mask;
PyDictEntry *ma_table;
PyDictEntry *(*ma_lookup)(PyDictObject *mp, PyObject *key, long hash);
PyDictEntry ma_smalltable[PyDict_MINSIZE];
};
При создании нового объекта словаря его размер равен 8. Это значение определяется константой PyDict_MINSIZE. Для хранения хэш-таблицы в PyDictObject были введены переменные ma_smalltable и ma_table. Переменная ma_smalltable с предвыделенной памятью размером PyDict_MINSIZE (то есть 8) позволяет небольшим словарям (до 8 объектов PyDictEntry) храниться без дополнительного выделения памяти. Эксперименты, проведённые разработчиками, показали, что этого размера вполне достаточно для большинства словарей: небольших словарей экземпляров и обычно небольших словарей, созданных для передачи именованных аргументов (kwargs). Переменная ma_table соответствует ma_smalltable для маленьких таблиц (то есть для таблиц из 8 ячеек). Для таблиц большего размера память ma_table выделяется отдельно. Переменная ma_table не может быть равна NULL.
Если кому-то вдруг захочется изменить значение PyDict_MINSIZE, это можно сделать в исходниках, а затем пересобрать Python. Значение рекомендуется делать равным степени двойки, но не меньше четырёх.
Ячейка в хэш-таблице может иметь три состояния
1) Неиспользованная (me_key == me_value == NULL)
Данное состояние означает, что ячейка не содержит и ещё никогда не содержала пару (ключ, значение).
После вставки ключа «неиспользованная» ячейка переходит в состояние «активная».
Это состояние – единственный случай, когда me_key = NULL и является начальным состоянием для всех ячеек в таблице.
2) Активная (me_key != NULL и me_key != dummy и me_value != NULL)
Означает, что ячейка содержит активную пару (ключ, значение).
После удаления ключа ячейка из состояния «активная» переходит в состояние «пустая» (то есть me_key = dummy, а
dummy = PyString_FromString("<dummy key>")).
Это единственное состояние, когда me_value != NULL.
3) Пустая (me_key == dummy и me_value == NULL)
Это состояние говорит о том, что ячейка ранее содержала активную пару (ключ, значение), но она была удалена, и новая активная пара ещё не записана в ячейку.
Так же как и при состоянии «неиспользованная», после вставки ключа ячейка из состояния «пустая» переходит в состояние «активная».
«Пустая» ячейка не может вернуться в состояние «неиспользованная», то есть вернуть me_key = NULL, так как в данном случае последовательность проб в случае коллизии не будет иметь возможность узнать, были ли ячейки «активны».
Переменные-члены структуры
ma_fill – число ненулевых ключей (me_key != NULL), то есть сумма «активных» и «пустых» ячеек.
ma_used – число ненулевых и не «пустых» ключей (me_key != NULL, me_key != dummy), то есть число «активных» ячеек.
ma_mask – маска, равная PyDict_MINSIZE — 1.
ma_lookup – функция поиска. По умолчанию при создании нового словаря используется lookdict_string. Так сделано потому, что разработчики посчитали, что большинство словарей содержат только строковые ключи.
Основные тонкости
Эффективность хэш-таблицы зависит от наличия «хороших» хэш-функций. «Хорошая» хэш-функция должна вычисляться быстро и с минимальным количеством коллизий. Но, к сожалению, наиболее часто используемые и важные хэш-функции (для строкового и целого типов) возвращают достаточно регулярные значения, что приводит к коллизиям. Возьмём пример:
>>> map(hash, [0, 1, 2, 3, 4])
[0, 1, 2, 3, 4]
>>> map(hash, ['abca', 'abcb', 'abcc', 'abcd', 'abce'])
[1540938117, 1540938118, 1540938119, 1540938112, 1540938113]
Для целых чисел хэшами являются их значения, поэтому подряд идущие числа будут иметь подряд идущие хэши, а для строк подряд идущие строки имеют практически подряд идущие хэши. Это не обязательно плохо, напротив, в таблице размером 2**i взятие i младших бит хэша как начального индекса таблицы выполняется очень быстро, и для словарей, проиндексированных последовательностью целых чисел, коллизий не будет вообще:

То же самое будет почти полностью соблюдаться, если ключи словаря – это «подряд идущие» строки (как в примере выше). В общих случаях это дает более чем случайное поведение, что и требуется.

Взятие только i младших бит хэша в качестве индекса также уязвимо к коллизиям: например, возьмём список [i << 16 for i in range(20000)] в качестве набора ключей. Так как целые являются их собственными хэшами и это вписывается в словарь размера 2**15 (так как 20000 < 32768), последние 15 бит от каждого хэша все будут равны 0.
>>> map(lambda x: '{0:016b}'.format(x), [i << 16 for i in xrange(20000)])
['0000000000000000', '10000000000000000', '100000000000000000', '110000000000000000', '1000000000000000000', '1010000000000000000', '1100000000000000000', '1110000000000000000', ...]
Получится, что все ключи будут иметь один и тот же индекс. То есть для всех ключей (кроме первого) произойдут коллизии.
Примеры специально подобранных «плохих» случаев не должны влиять на обычные случаи, так что просто оставим взятие последних i бит. Всё остальное отдаётся на откуп методу разрешения коллизий.
Метод разрешения коллизий
Процедура выбора подходящей ячейки для вставки элемента в хэш-таблицу называется пробирование, а рассматриваемая ячейка-кандидат – проба.
Обычно ячейка находится с первой попытки (и это действительно так, ведь коэффициент заполнения хэш-таблицы держится ниже 2/3), что позволяет не тратить время на пробирование и делает расчет начального индекса очень быстрым. Но давайте рассмотрим, что случится, если произойдёт коллизия.
Первая часть метода разрешения коллизий заключается в расчёте индексов таблицы для пробирования с помощью формулы:
j = ((5 * j) + 1) % 2**i
Для любого начального j в пределах [0..(2**i — 1)] вызов данной формулы 2**i раз вернёт каждое число в пределах [0..(2**i — 1)] ровно один раз. Например:
>>> j = 0
>>> i = 3
>>> for _ in xrange(0, 2**i):
... print j,
... j = ((5 * j) + 1) % 2**i
...
0 1 6 7 4 5 2 3
Вы скажете, что это ничем не лучше использования линейного пробирования с постоянным шагом, ведь в данном случае ячейки в хэш-таблице также просматриваются в определенном порядке, но это не единственное отличие. В общих случаях, когда хэш значения ключей идут подряд, данный метод лучше линейного пробирования. Из примера выше можно проследить, что для таблицы размером 8 (2**3) порядок индексов будет следующим:
0 -> 1 -> 6 -> 7 -> 4 -> 5 -> 2 -> 3 -> 0 -> … (затем идут повторения)
Если произойдёт коллизия для пробы с индексом, равным 5, то следующий индекс пробы будет 2, а не 6, как в случае линейного пробирования с шагом +1, поэтому для ключа, добавляемого в будущем, индекс пробы которого будет равен 6, коллизии не произойдёт. Линейное пробирование в данном случае (при последовательных значениях ключей) было бы плохим вариантом, так как происходило бы много коллизий. Вероятность же того, что хэш значения ключей будут идти в порядке 5 * j + 1, намного меньше.
Вторая часть метода разрешения коллизий заключается в использовании не только младших i бит хэша, но и остальных бит тоже. Это реализовано с использованием переменной perturb следующим образом:
j = (5 * j) + 1 + perturb
perturb >>= PERTURB_SHIFT
затем j % 2**i используется как следующий индекс пробы
где:
perturb = hash(key)
PERTURB_SHIFT = 5
После этого последовательность проб будет зависеть от каждого бита хэша. Псевдослучайное изменение очень эффективно, потому что быстро увеличивает различия в битах. Так как переменная perturb – беззнаковая, то, если пробирование выполняется достаточно часто, переменная perturb в конечном итоге становится и остаётся равной нулю. В этот момент (который достигается очень редко) результат j снова становится равен 5 * j + 1. Далее поиск происходит точно так же, как в первой части метода, и свободная ячейка в конечном счете будет найдена, поскольку, как было сказано ранее, каждое число в диапазоне [0..(2**i — 1)] будет возвращено ровно один раз, и мы уверены, что всегда есть по крайней мере одна «неиспользованная» ячейка.
Выбор «хорошего» значения для PERTURB_SHIFT – это вопрос балансировки. Если сделать его малым, то старшие биты хэша будут влиять на последовательность проб по итерациям. Если же сделать его большим, то в действительно «плохих» случаях старшие биты хэша будут оказывать влияние только на ранних итерациях. В результате экспериментов, которые провёл один из разработчиков Python – Тим Питерс, значение PERTURB_SHIFT было выбрано равным 5, так как это значение оказалось «лучшим». То есть показало минимальное общее число коллизий как для нормальных, так и для специально подобранных «плохих» случаев, хотя значения 4 и 6 не были значительно хуже.
Историческая справка: Один из разработчиков Python, Реймер Берендс, предлагал идею использования подхода расчёта индексов таблицы, основанного на многочленах, который затем был улучшен Кристианом Тисмером. Этот подход также показал отличные результаты по возникновению коллизий, но требовал больше операций, а также дополнительной переменной для хранения многочлена таблицы в структуре PyDictObject. В экспериментах Тима Питерса текущий, используемый в Python метод оказался быстрее, показывая в равной степени хорошие результаты по возникновению коллизий, но требовал меньше кода и использовал меньше памяти.
Инициализация словаря
Когда вы создаёте словарь, вызывается функция PyDict_New. В этой функции последовательно выполняются следующие операции: происходит выделение памяти для нового объекта словаря PyDictObject. Переменная ma_smalltable очищается. Переменные ma_used и ma_fill приравниваются 0, ma_table становится равной ma_smalltable. Значение ma_mask приравнивается PyDict_MINSIZE — 1. Функция для поиска ma_lookup делается равной lookdict_string. Возвращается созданный объект словаря.
Добавление элемента
При добавлении элемента в словарь или изменении значения элемента в словаре вызывается функция PyDict_SetItem. В этой функции берётся значение хэша и вызывается функция insertdict, а также функция dictresize, если таблица заполняется на 2/3 от текущего размера.
В свою очередь в функции insertdict происходит вызов lookdict_string (или lookdict, если в словаре есть не строковый ключ), в которой происходит поиск свободной ячейки в хэш-таблице для вставки. Эта же функция используется для нахождения ключа при извлечении.
Начальный индекс пробы в этой функции рассчитывается как хэш ключа, поделённый по модулю на размер таблицы (таким образом, происходит взятие младших бит хэша). То есть:
>>> PyDict_MINSIZE = 8
>>> key = 123
>>> hash(key) % PyDict_MINSIZE
>>> 3
В Python это реализовано с использованием логической операции «И» и маски. Маска равна следующему значению: mask = PyDict_MINSIZE — 1.
>>> PyDict_MINSIZE = 8
>>> mask = PyDict_MINSIZE - 1
>>> key = 123
>>> hash(key) & mask
>>> 3
Так получаются младшие биты хэша:
2**i = PyDict_MINSIZE, отсюда i = 3, то есть достаточно трёх младших бит.
hash(123) = 123 = 11110112
mask = PyDict_MINSIZE — 1 = 8 — 1 = 7 = 1112
index = hash(123) & mask = 11110112 & 1112 = 0112 = 3
После того как индекс рассчитан, выполняется проверка ячейки по индексу, и если она «неиспользованная», то в неё добавляется запись (хэш, ключ, значение). Но если эта ячейка занята, из-за того, что другая запись имеет тот же хэш (то есть произошла коллизия), выполняется сравнение хэша и ключа вставляемой записи и записи в ячейке. Если хэш и ключ для записей совпадают, то считается, что запись уже существует в словаре, и выполняется её обновление.
Это объясняет хитрый момент, связанный с добавлением равных по значению, но разных по типу ключей (к примеру, float, int и complex):
>>> 7.0 == 7 == (7+0j)
True
>>> d = {}
>>> d[7.0]='float'
>>> d
{7.0: 'float'}
>>> d[7]='int'
>>> d
{7.0: 'int'}
>>> d[7+0j]='complex'
>>> d
{7.0: 'complex'}
>>> type(d.keys()[0])
<type 'float'>
То есть тот тип, который был добавлен в словарь первым, и будет типом ключа, несмотря на обновление. Это объясняется тем, что реализация хэша для float значений возвращает хэш от int, если дробная часть равна 0.0. Пример расчёта хэша для float, переписанный на Python:
def float_hash(float_value):
...
fractpart, intpart = math.modf(float_value)
if fractpart == 0.0:
return int_hash(int(float_value)) # использовать хэш int
...
А хэш от complex возвращает хэш от float. В данном случае возвращается хэш только действительной части, так как мнимая часть равна нулю:
def complex_hash(complex_value):
hashreal = float_hash(complex_value.real)
if hashreal == -1:
return -1
hashimag = float_hash(complex_value.imag)
if hashimag == -1:
return -1
res = hashreal + 1000003 * hashimag
res = handle_overflow(res)
if res == -1:
res = -2
return res
Пример:
>>> hash(7)
7
>>> hash(7.0)
7
>>> hash(7+0j)
7
Ввиду того, что и хэши, и значения для всех трёх типов равны, выполняется простое обновление значения найденной записи.
Замечание по поводу добавления элементов: Python запрещает добавление элементов в словарь во время итерации, поэтому при попытке добавить новый элемент произойдёт ошибка:
>>> d = {'a': 1}
>>> for i in d:
... d['new item'] = 123
...
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
RuntimeError: dictionary changed size during iteration
Вернёмся к процедуре добавления элемента в словарь. После успешного добавления или обновления записи в хэш-таблице происходит сравнение следующей записи-кандидата на вставку. Если хэш или ключ у записей не совпадают, начинается пробирование. Происходит поиск «неиспользованной» ячейки для вставки. В данной реализации Python используется случайное (а если переменная perturb равна нулю – квадратичное) пробирование. Как было описано выше, при случайном пробировании индекс следующей ячейки выбирается псевдослучайным образом. Запись добавляется в первую найденную «неиспользованную» ячейку. То есть два ключа a и b, у которых hash(a) == hash(b), но a != b могут легко существовать в одном словаре. В случае если ячейка по начальному индексу пробы «пустая», произойдёт пробирование. И если первая найденная ячейка будет «нулевая», то «пустая» ячейка будет использована заново. Это позволяет перезаписать удалённые ячейки, сохраняя ещё неиспользованные.
Получается, что индексы добавляемых в словарь элементов зависят от уже находящихся в нём элементов, и порядок ключей для двух словарей, состоящих из одного и того же набора пар (ключ, значение), может быть разным и определяется очерёдностью добавления элементов:
>>> d1 = {'one': 1, 'two': 2, 'three': 3, 'four': 4, 'five': 5}
>>> d2 = {'three': 3, 'two': 2, 'five': 5, 'four': 4, 'one': 1}
>>> d1 == d2
True
>>> d1.keys()
['four', 'three', 'five', 'two', 'one']
>>> d2.keys()
['four', 'one', 'five', 'three', 'two']
Это объясняет, почему словари в Python при выводе содержимого отображают хранимые пары (ключ, значение) не в порядке их добавления в словарь. Словари выводят их в порядке расположения в хэш-таблице (то есть в порядке индексов).
Рассмотрим пример:
>>> d = {}
>>> d['habr'] = 1
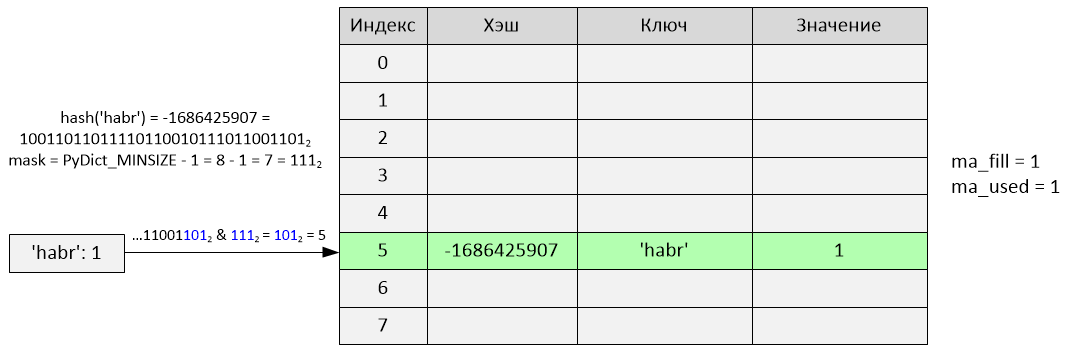
Произошла вставка по индексу 5. Переменные ma_fill и ma_used стали равны 1.
>>> d['python'] = 2
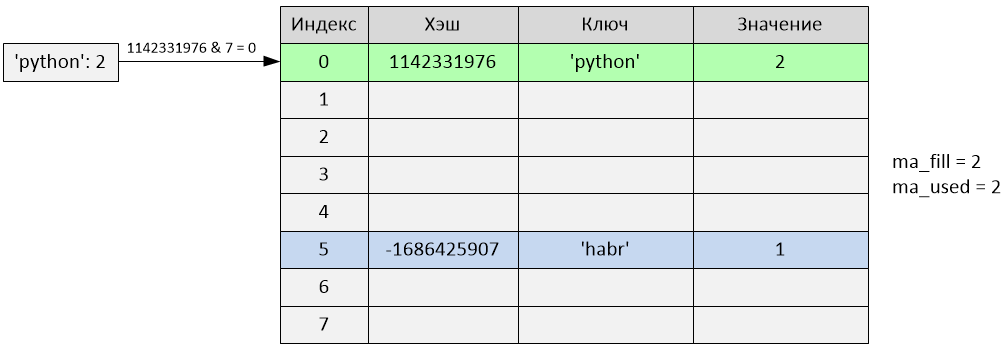
Произошла вставка по индексу 0. Переменные ma_fill и ma_used стали равны 2.
>>> d['dict'] = 3
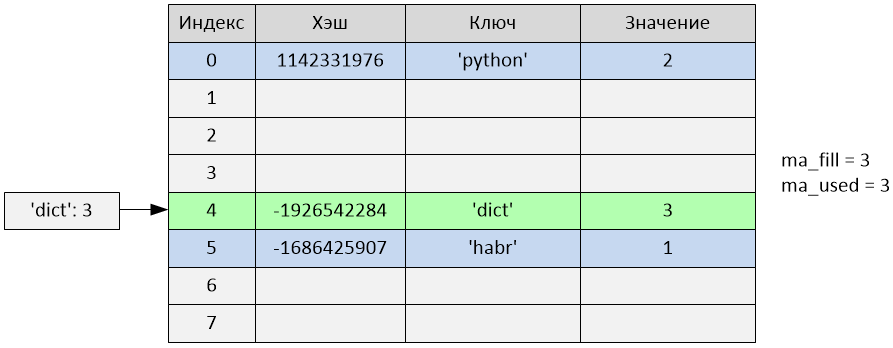
Произошла вставка по индексу 4. Переменные ma_fill и ma_used стали равны 3.
>>> d['article'] = 4
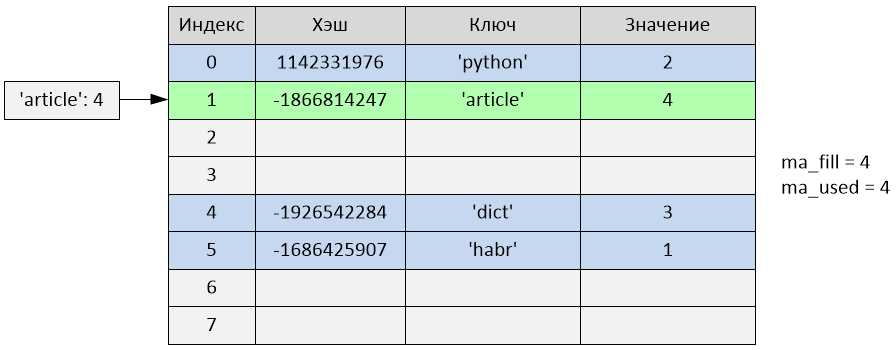
Произошла вставка по индексу 1. Переменные ma_fill и ma_used стали равны 4.
>>> d['!!!'] = 5
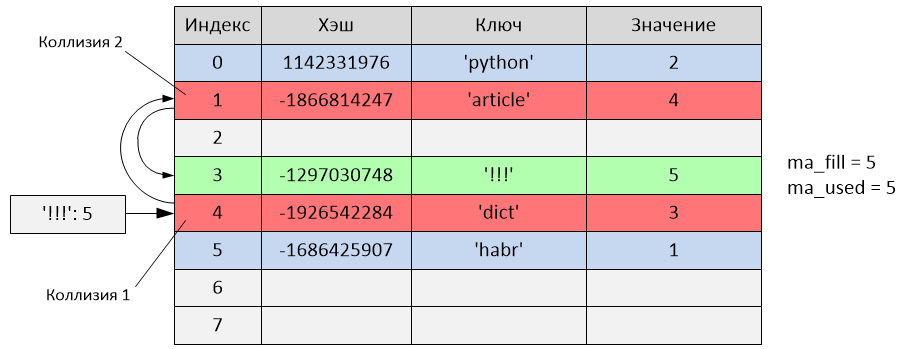
Произошло следующее:
hash('!!!') = -1297030748
i = -1297030748 & 7 = 4
Но как видно из таблицы, индекс 4 уже занят записью с ключом 'dict'. То есть произошла коллизия. Начинается пробирование:
perturb = -1297030748
i = (i * 5) + 1 + perturb
i = (4 * 5) + 1 + (-1297030748) = -1297030727
index = -1297030727 & 7 = 1
Новый индекс пробы равен 1, но данный индекс тоже занят (записью с ключом 'article'). Произошла ещё одна коллизия, продолжаем пробирование:
perturb = perturb >> PERTURB_SHIFT
perturb = -1297030748 >> 5 = -40532211
i = (i * 5) + 1 + perturb
i = (-1297030727 * 5) + 1 + (-40532211) = -6525685845
index = -6525685845 & 7 = 3
Новый индекс пробы равен 3, и, так как он не занят, происходит вставка записи с ключом '!!!' в ячейку с третьим индексом. В данном случае запись была добавлена после двух проб из-за произошедших коллизий. Переменные ma_fill и ma_used стали равны 5.
>>> d
{'python': 2, 'article': 4, '!!!': 5, 'dict': 3, 'habr': 1}
Пробуем добавить шестой элемент в словарь.
>>> d[';)'] = 6
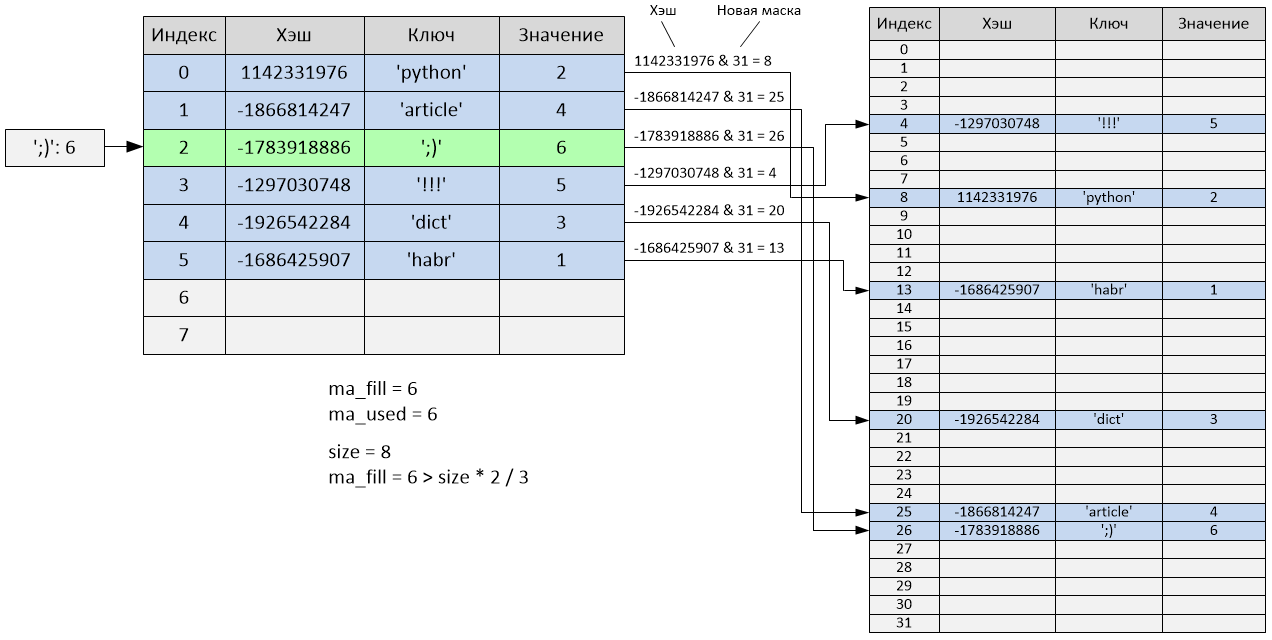
После добавления шестого элемента таблица будет заполнена на 2/3, а соответственно, произойдёт изменение её размера. После того как размер изменится (в данном случае увеличится в 4 раза), произойдёт полная перестройка хэш-таблицы с учётом нового размера – все «активные» ячейки будут перераспределены, а «пустые» и «неиспользованные» ячейки будут проигнорированы.
Размер хэш-таблицы теперь равен 32, а переменные ma_fill и ma_used стали равны 6. Как видно, порядок элементов полностью поменялся:
>>> d
{'!!!': 5, 'python': 2, 'habr': 1, 'dict': 3, 'article': 4, ';)': 6}
Поиск элемента
Поиск записи в хэш-таблице словаря происходит аналогично, начинаясь с ячейки i, где i зависит от хэша ключа. Если хэш и ключ не совпадают с хэшом и ключом найденной записи (то есть была коллизия и надо найти подходящую запись) – начинается пробирование, которое продолжается, пока не будет найдена запись, для которой хэш и ключ совпадают. Если же все ячейки были просмотрены, но запись не найдена, возвращается ошибка.
>>> d = {'a': 123, 'b': 345, 'c': 678}
>>> d['x']
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'x'
Коэффициент заполнения хэш-таблицы
Размер таблицы изменяется, когда она заполняется на 2/3. То есть для начального размера хэш-таблицы словаря, равного 8, изменение произойдёт после того, как будет добавлен 6 элемент.
>>> 8 * 2.0 / 3
5.333333333333333
При этом происходит перестройка хэш-таблицы с учётом её нового размера, а соответственно, меняются и индексы всех записей.
Значение 2/3 от размера было выбрано как оптимальное, для того чтобы пробирование не занимало слишком много времени, то есть вставка новой записи происходила быстро. Увеличение этого значения приводит к тому, что словарь плотнее заполняется записями, что в свою очередь увеличивает количество коллизий. Уменьшение же увеличивает разреженность записей в ущерб увеличения занимаемых ими кэш-линий процессора и в ущерб увеличения общего объема памяти. Проверка заполнения таблицы происходит в весьма чувствительном ко времени участке кода. Попытки сделать проверку более сложной (например, изменяя коэффициент заполнения для разных размеров хэш-таблицы) уменьшали производительность.
Проверить, что размер словаря действительно изменяется, можно так:
>>> d = dict.fromkeys(range(5))
>>> d.__sizeof__()
248
>>> d = dict.fromkeys(range(6))
>>> d.__sizeof__()
1016
В примере возвращается размер всего объекта PyDictObject для 64-битной версии ОС.
Начальный размер таблицы равен 8. Таким образом, когда число заполненных ячеек будет равно 6 (то есть больше 2/3 от размера), размер таблицы увеличится до 32. Затем, когда число будет равно 22, увеличится до 128. При 86 увеличится до 512, при 342 – до 2048 и так далее.
Коэффициент увеличения размера таблицы
Коэффициент увеличения размера таблицы при достижении максимального уровня заполнения равен 4, если размер таблицы меньше 50000 элементов, и 2 – для таблиц большего размера. Такой подход может быть полезен приложениям с ограничениями по памяти.
Увеличение размера таблицы улучшает среднюю разреженность, то есть разбросанность записей по таблице словаря (уменьшая коллизии), за счёт увеличения объема потребляемой памяти и скорости итераций, а также уменьшает количество дорогостоящих операций выделения памяти при изменении размера для растущего словаря.
Обычно добавление элемента в словарь может увеличить его размер в 4 или 2 раза в зависимости от текущего размера словаря, но также возможно, что размер словаря уменьшится. Такая ситуация может произойти, если ma_fill (количество ненулевых ключей, сумма «активных» и «пустых» ячеек) намного больше ma_used (количество «активных» ячеек), то есть много ключей было удалено.
Удаление элемента
При удалении элемента из словаря вызывается функция PyDict_DelItem.
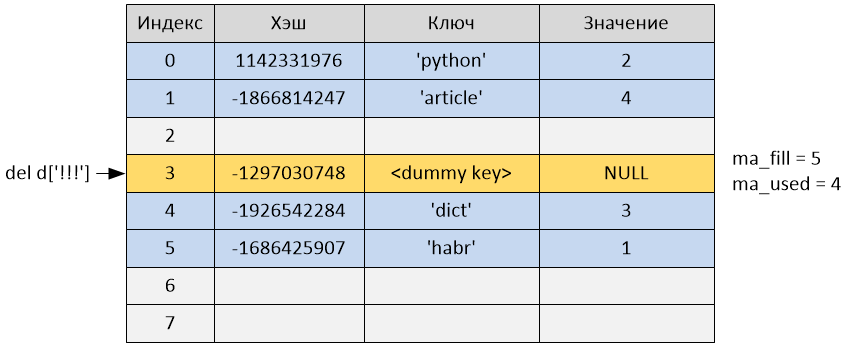
Удаление из словаря происходит по ключу, хотя в действительности освобождения памяти не происходит. В этой функции вычисляется хэш значение ключа, а затем происходит поиск записи в хэш-таблице с использованием всё той же функции lookdict_string или lookdict. В случае если запись с таким ключом и хэшем найдена, ключ этой записи выставляется в состояние «пустой» (то есть me_key = dummy), а значение записи – в NULL (me_value = NULL). После этого переменная ma_used уменьшится на единицу, а ma_fill останется без изменения. Если же запись не найдена, возвращается ошибка.
>>> del d['!!!']
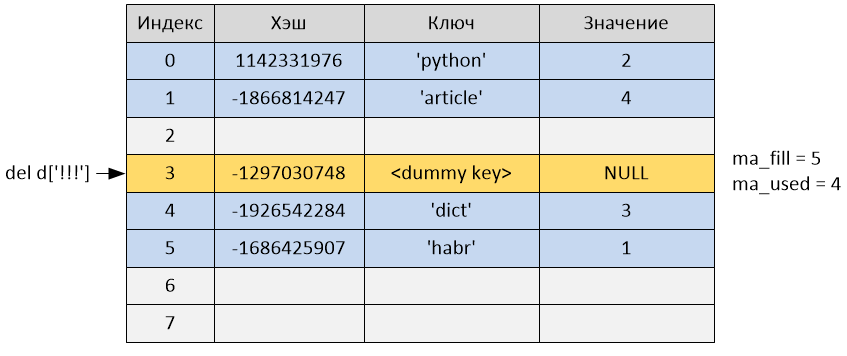
После удаления переменная ma_used стала равна 4, а ma_fill осталась равной 5, так как ячейка не была удалена, а всего лишь была помечена как «пустая» и продолжает занимать ячейку в хэш-таблице.
Рандомизация хэшей
При запуске python можно воспользоваться ключом -R, чтобы использовать псевдослучайную «соль». В этом случае хэш значения таких типов, как строки, buffer, bytes, и объекты datetime (date, time и datetime) будут непредсказуемыми между вызовами интерпретатора. Данный способ предложен в качестве защиты от DoS атак.
Ссылки
github.com/python/cpython/blob/2.7/Objects/dictobject.c
github.com/python/cpython/blob/2.7/Include/dictobject.h
github.com/python/cpython/blob/2.7/Objects/dictnotes.txt
www.shutupandship.com/2012/02/how-hash-collisions-are-resolved-in.html
www.laurentluce.com/posts/python-dictionary-implementation
rhodesmill.org/brandon/slides/2010-03-pycon
www.slideshare.net/MinskPythonMeetup/ss-26224561 – Dictionary в Python. По мотивам Objects/dictnotes.txt – SlideShare (Cyril notorca Lashkevich)
www.youtube.com/watch?v=JhixzgVpmdM – Видео доклада «Dictionary в Python. По мотивам Objects/dictnotes.txt»