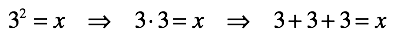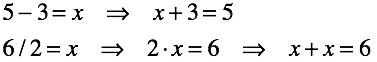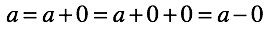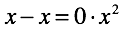Часть 1. Вобще-то уже все поделили до нас!
Часть 2. Истина где-то рядом
В прошлой части мы расширяли алгебру и смогли делить на ноль арифметически. В качестве бонуса, способ оказался не единственным. Однако, все эти алгебры не дали ответа на вопрос: “Что там внутри или почему нам это не показывают?”
Пока древние вязали узелки, такой вопрос возникнуть не мог. Сейчас, куда не глянь, “бла-бла, для а≠0”. Значит ответ затаился где-то между узелками и настоящим. В математике все строго и последовательно, а значит и ответ не мог потеряться.

Мы попробуем приблизиться к ответу настолько близко насколько это возможно. Эта часть практически полностью посвящена философии арифметики. Скорее всего часть материала будет для Вас тривиальной. Однако у нас тут не повтор школьного курса арифметики.
Материал построен так, чтобы выделить структуру арифметики. Мы будем вгрызаться в нее с разных сторон и отрывать слои. Цель — понять, что на чем лежит.
Чтобы снова броситься в дебри, хотелось бы понять, почему этот вопрос периодически возникает и ради чего стоит искать ответ.
Давайте вспомним школьные годы, то время, когда нам впервые сказали: “На ноль делить нельзя, — вот так вот категорично. — Нельзя и все!”. А ведь до того в математике все было логично и последовательно. Складывали арбузы и вычитали дыни, яблоки перекатывали. Откуда не возьмись, на самом старте изучения математики, появился первый запретный плод.
Но система образования не щадит никого (пруф). Нет другого выхода, кроме как идти дальше и осваивать новые знания. В голове происходит “скачок знаний”, как будто тысячелетие эволюции математики было пропущено. И это только начало.

В старших классах, откуда ни возьмись, появляются формулы окружности и треугольников, дискриминант, тригонометрические тождества и т.п. Что их объединяет? Все они пришли сверху, совершенно неизвестно откуда. Их нужно просто использовать, в худшем случае зазубрить.
Оказавшись в ВУЗе, большинство, вместо возвращения к пропущенному материалу, изучает «вышку» с уклоном в специальность. Объем формул, пришедших свыше, уже совершенно не смущает.
Да, систему образования понять можно. Специалисту платят за результат, а не за то что он знает откуда экспонента в его расчетах.
В итоге мы не приходим к выводам, так как это делают математики. В момент “скачка знаний”, то есть когда мы отбрасываем часть логических цепочек, вершится таинство. Мы принимаем на веру то что нам говорят. Учебник превращается в священное писание!

Запрет деления на ноль — это первый и самый навязчивый запрет математики. Поэтому он запоминается на всю жизнь. Это так же педагогическая проблема, которая оставляет отпечаток на всю математику, как на “тайну покрытую мраком”. Это сложная проблема, по сравнению с ней найти большинство пропущенных логических цепочек не составляет труда.
Превратить священное писание назад в учебник можно. Причина запрета должна стать строго определенной. Задача педагогов преподнести ее ясно. Наука не должна сеять сомнения.
Капитан Очевидность утверждает, чтобы поделить на ноль нужно знать что такое деление и что такое ноль. Как ни печально, гугл подсказывает, что многие адепты “магии деления на ноль” не проходят даже первый круг этого ада. А именно понять что они собираются сделать и с чем. Заглянем в Википедию:

Похоже, самое полезное, что мы здесь нашли — это связь между операциями. Можно сказать что деление — вино третьего отжима, умножение и вычитание — второго, а сложение — первого. Возможно, именно по этой причине деление стало давать сбой при работе с нулем.
Итак, только операция сложения содержит правило о том, как по двум исходным аргументам (слагаемым) определить результат операции (сумму). Все остальные арифметические операции используют данное правило (соответствие чисел), но вдобавок накладывают свои “дополнительные условия”.

В зависимости от “дополнительных условий” арифметические операции можно поделить на прямые и обратные:
Все прямые операции обладают одним свойством. Они являются замкнутыми. То есть тип результата полностью определяется типами входных чисел (невозможно получить из произведения двух целых чисел дробный результат).
Обратные операции являются замкнутыми только частично (значение корня из целого числа может оказаться целым числом, а может и не оказаться). В тех случаях, где подобрать результат не удается операция оказывается не определена. Данную проблему издавна решают простым способом: рассматривают получившуюся запись операции и числа как новый тип чисел: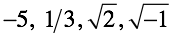 .
.
Таким образом, можно сказать что обратные операции и “порождают” новые типы чисел.
Математическим языком:
Попробуем структурировать наше представление об арифметических операциях и порождаемых ими типах чисел. Для наглядности представим один из вариантов, как может идти эволюция арифметики.
Мы в пещере. С умением считать никто не родился. Однако в процессе “созерцания” появилось понимание, что такое понятие “количество”. То есть мы знаем что два мамонта и два яблока имеют нечто общее и можем это выразить, загибая пальцы. Соответственно ничего, кроме натуральных чисел на этом этапе мы не знаем.
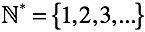
Множество натуральных чисел помечено звездочкой “*” для однозначности. Здесь и далее подчеркивается отсутствие понятия “ноль”.
Есть несколько формальных определений последовательности натуральных чисел. Мы возьмем за основу аксиомы Пеано. Примечательно что эти определения не были описаны древними. Они появились только в 19 веке, а после прошли процедуру уточнения (в первоначальном варианте их было девять, в современном виде уже пять).
Рассмотрим формальные определения и их суть в рамках нашей задачи (традиционное словесное описание можно найти на Википедии):
Какой вывод можно сделать из этих аксиом? Вводится запрет на закольцованность в любом виде (глобальную или локальную). Запрет на закольцованность всегда требует наличие следующего элемента. Так появляется математическое понятие “бесконечность” основанное на понятии «количество”. Понятие “бесконечность” не может существовать без понятия „количество”.
Математическим языком:
Первая операция, возникшая в ходе нашей эволюции. Как целые пальцы не загибай, результат будет целым. Разве что у вождя сумма пальцев может быть чуть больше чем у всех остальных. Если пальцев не хватает, всегда можно позвать научного ассистента по пещере и расширить разрядную сетку.
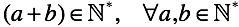
В четверг охотники подстрелили 12 мамонтов. За пятницу съели 5 штук. Сколько мамонтов осталось?

Задача хорошо решается путем введения разгибания пальцев. Но подход работает не всегда. Например, чтобы оценить запасы на выходные охотник загибает семь пальцев за остаток, разгибает пять пальцев за субботу (норма расхода в день) и “пытается” разжать за воскресенье.

В этот момент между “try” и “catch” возникает ArithmeticException. Результат оказывается не определен. Наша операция определена только для случая, когда уменьшаемое больше вычитаемого.
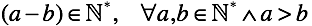
Однако определение вычитания не накладывает никаких ограничений. Чтобы избавиться от требования “a > b” введем “правило перестановки”. То есть позволим менять местами уменьшаемое и вычитаемое. Но чтобы тождество оставалось верным результат нужно пометить каким-то маркером, например знаком “минус”. Всякие маркеры для математики — дело обычное (например, признак отсутствия нуля у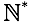 ).
).
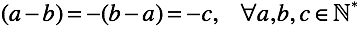
За счет вспомогательной операции “перестановки” мы подошли к первой абстракции — “отрицательные числа”. Пометка в виде знака “минус” у натурального числа есть ничто иное как признак отложенного вычитания (но это только пока).
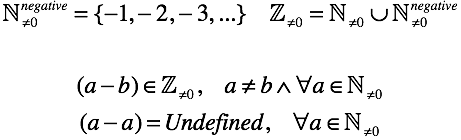
У нас остался всего один не определенный случай, когда уменьшаемое и вычитаемое равны. Если мы захотим определить его, то нам придется ответить на вопрос что такое понятие “ничто”. Хотя к чему все эти сложности, обозначим “ничто” символом “0” (позже вникнем по полной).

Осталось зафиксировать наше решение в виде “правил сложения/вычитания нуля”. Они следуют из определения нуля после пары нехитрых перестановок:
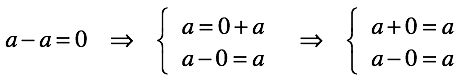
Посмотрим, насколько хорошо работают введенные правила. Решая уравнения, мы по двум известным числам всегда можем найти неизвестное третье. Совершенно неважно в какой части уравнения оно стоит, решение всегда однозначно.
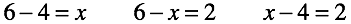
Отрицательные числа появились в результате перестановки, ноль же заполнил “ничто”. Отрицательные числа и ноль рождены разными способами. Далее мы будем рассматривать две ветви эволюции: отдельно всех чисел без нуля и отдельно ноль.
Умножение по определению является сокращенной записью сложения. Умножая натуральные числа, результат может быть только натуральным. На этом этапе эволюции для нас польза от определения заканчивается.
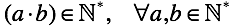
Для отрицательных чисел в определении нет ни слова о том как их перемножать. Эти правила сформировались постепенно в ходе решения прикладных задач. В современной трактовке они известны как дополнение к умножению в виде “правил знаков”. Они определены настолько хорошо, что применяя их к целым не нулевым числам, операция остается замкнутой.
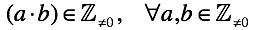
В случае нуля ситуация отличается кардинально. Вводится еще одно правило “правило умножения нуля“ (умножение любого числа на ноль дает ноль). Но новым это правило только кажется. Ввести какое либо иное правило мы не можем. Определение умножения жестко связывает нас со сложением. Раскрывая умножение через сложение, мы используем “правила сложения/вычитания нуля”, соответственно ничего кроме нуля мы получить не можем.
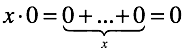
Математическим языком:
Деление — операция обратная умножению. В уравнениях с положительными и отрицательными числами появляется возможность подстановки не кратных чисел.
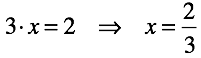
Как следствие операция порождает “рациональные числа”.
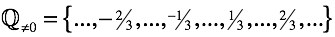
Чтобы вписать их в арифметику, в комплекте идут “правила действий с обыкновенными дробями”. К счастью, эти правила гармонично сосуществуют с введенными нами ранее “правилами знаков”. В итоге в уравнениях сохраняется возможность определить по двум известным числам неизвестное при любой расстановке.
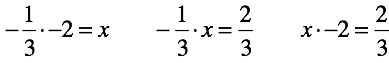
В случае нуля его можно умножать на рациональные числа. На этом всё, гармония закончилась! Только для двух из трех видов уравнений с произвольными числами решение может быть найдено.
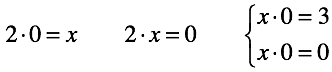

Во-первых, появилась возможность составить уравнение с настолько не удобными числами, что мы не сможем подобрать ни одного решения. Решение “не возможно”.
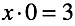
Во-вторых, появилась возможность составить уравнение в котором есть бесконечное множество решений. Выбрать какое-то одно из них так же невозможно. Решение “не однозначно”.

Несложно догадаться, корень проблемы деления на ноль лежит в “невозможности” и “неоднозначности” умножения нуля. Умножение, в свою очередь, ретранслирует “правила сложения/вычитания нуля”. По сути можно задать уравнения, обладающие такими же свойствами, используя только сложение.
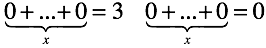
В обоих уравнениях нужно определить количество нулей, которые нужно сложить чтобы получить произвольное число или ноль.
Деление не привнесло чего-то качественно нового. Произошла трансформация “невозможности” и “неоднозначности” сложения в конкретные сущности, в неопределенности вида 1/0 и 0/0 соответственно.

Получается что деление, как первый подозреваемый, не виновато в том что на ноль делить нельзя.

Пока не существует понятия “ноль” все операции, включая возведение в степень и взятие корня (логарифмирование), хорошо замкнуты (уже правда на комплексных числах) и арифметика работает великолепно. Но есть одно “но”, при такой конфигурации арифметики операция вычитания, оказывается определена не полностью.
После введения нуля сложение и вычитание неплохо работает. Для остальных операций он скорее повод для установки костылей (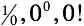 ), нежели равноправное число.
), нежели равноправное число.
Итак, раз операция деления оказалась не виновата в запрете деления на ноль. Попробуем тогда собрать воедино все, что мы знаем о нуле:
На последнем пункте стоит остановиться поподробнее. Попробуем представить не абсолютный ноль.
Допустим, у нас есть мамонт. Для его перевозки нужна тара. Если положить мамонта в тару, а потом вытащить, то в таре окажется “ничто” (прям как на картинке со спичкой выше). Однако тара для двух мамонтов несколько отличается от тары для одного. В случае кражи есть основание выставлять обвинение в соответствии с размером оставшейся тары. А значит, существуют ситуации когда одно “ничто” другому “ничто” рознь.

Может ли “ничто” быть разным или “ничто” есть единая и абсолютная сущность? Это вопрос на который невозможно дать ответ. Аналогичен и бессмысленен спор на тему есть ли Бог, а и есть то единый он или их много. Ответа на этом свете мы не узнаем.
Математическим языком:

Хорошо, ответа на вопрос сколько должно быть нулей арифметика дать не может. Мы пользуемся одним нулем. В колесах, рассмотренных в первой части, использовалась арифметика с бесконечным количеством нулей. А может ли быть конечное число нулей, но больше одного.
Может и такие арифметики успешно используются. Один из ярких примеров арифметика со “знаковым нулем”, реализованная в JavaScript.
Математическим языком:
Можно сделать вывод, что неопределенности в арифметике будут сохраняться до тех пор, пока количество нулей конечно.
По большому счету неважно как мы будем относиться к нулю. Нужен ли нам единый и абсолютный ноль, а может парочка или вообще бесконечное количество, арифметика всегда сможет под нас подстроиться.

Напоследок, хотелось бы представить хотя бы один вариант числовой оси содержащей бесконечное количество нулей (данный пример описывает концепцию и не претендует на математическую строгость).
Для вычитания, когда уменьшаемое и вычитаемое равны, вместо ввода нуля определим операцию “сокращения”. То есть разрешаем вычеркивать эквивалентные выражения с противоположным знаком. Но если мы сократили все, то результат уже не пригоден к дальнейшему использованию.
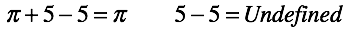
Отсчет в числовой оси начнем с единицы (от первого числа зародившего понятие “количество”). Для генерации остальных чисел воспользуемся бесконечной последовательностью, определенной функцией следования (она же использована в аксиомах Пеано). Это будет наш эталонный генератор бесконечной последовательности.
Чтобы получить очень маленькое число при помощи функции следования нужно затратить столько же сил сколько и на генерацию очень большого. Используем функции f(x)=1/x и f(x)=x. Приводить в десятичный вид рациональную дробь задача не стоит, соответственно вычислительная сложность функций одинакова.
Так как ни “абсолютный ноль“ (отмечен символом ноль), ни »потенциальная бесконечность" (отмечена символом беззнаковой бесконечности) недостижимы, ось растет из единицы бесконечно в обоих направлениях (масштаб неравномерный).

При определении вычитания определено “правило перестановки”. Мы же, в свою очередь, делаем копию нашей прямой и отображаем ее зеркально. Числа-близнецы и недостижимые для них пределы помечаем знаком “минус”. Положительная прямая, не соединена с отрицательной. Переход из одной прямой в другую выполняется только за счет “правила перестановки”.
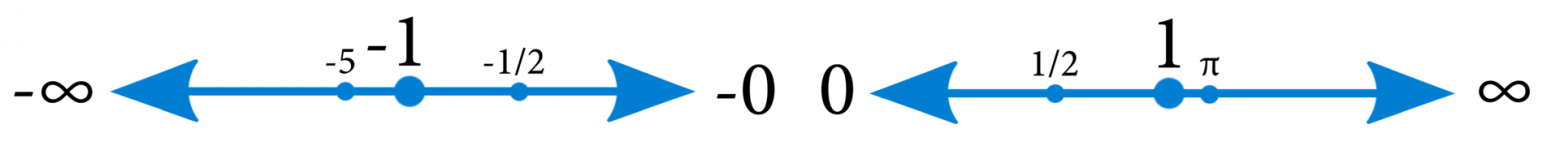
Для наглядности изобразим полученную числовую прямую в виде круга. Так же, как мы делали при проективном расширении. Однако, предельные значения не смыкаем (компактификацию не выполняем). Данная трансформация смысловой нагрузки не несет и выполнена только для улучшения восприятия.
Теперь мы готовы к самому главному. Выполним переход от единой потенциальной бесконечности к бесконечному множеству актуальных бесконечностей (аналогичный подход используется в нестандартном анализе).
Будем относится к бесконечно большим величинам как к полноправным числам. За эталонную актуальную бесконечность возьмем “скорость” с которой функция следования достигает любого произвольного числа. Обозначим это число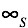 . Не стоит его путать с потенциальной бесконечностью
. Не стоит его путать с потенциальной бесконечностью  , она все так же недостижима.
, она все так же недостижима.
Для получения различных актуальных бесконечностей будем использовать понятие предела функции при стремлении к числу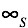 . Мы не будем отбрасывать бесконечно малые (низшего порядка) и не будем поглощать константы бесконечно большими величинами, как это принято в классическом анализе. Мы будем сохранять всю информацию, составляющую число. Соответственно, у нас появляется возможность сравнения бесконечно больших чисел.
. Мы не будем отбрасывать бесконечно малые (низшего порядка) и не будем поглощать константы бесконечно большими величинами, как это принято в классическом анализе. Мы будем сохранять всю информацию, составляющую число. Соответственно, у нас появляется возможность сравнения бесконечно больших чисел.

Возводя число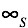 в отрицательные степени, мы получаем бесконечно малые числа. По сути это и есть наше бесконечное множество нулей, которые можно сравнить между собой и использовать в арифметике (в отличие от бесконечно малой величины в классическом анализе).
в отрицательные степени, мы получаем бесконечно малые числа. По сути это и есть наше бесконечное множество нулей, которые можно сравнить между собой и использовать в арифметике (в отличие от бесконечно малой величины в классическом анализе).
Математическим языком:
Если возникнет практическая необходимость, можно определить операцию вычитания и для равных чисел (вместо “сокращения” определенного нами выше). Например, это может быть число низшего порядка, нежели исходные числа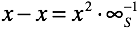 (аналог уравнения из колеса). Арифметика окажется замкнутой. Но нужно отдавать себе отчет, что сумма двух двоек тут же окажется равной четырем с хвостиком. Это чем-то похоже на сложение скоростей в теории относительности. Еще один пример, термодинамика и понятие абсолютного нуля температуры. Остановив молекулы, атомы продолжают движение. Остановив атомы, кварки все еще двигаются и т.д. Погружение бесконечно.
(аналог уравнения из колеса). Арифметика окажется замкнутой. Но нужно отдавать себе отчет, что сумма двух двоек тут же окажется равной четырем с хвостиком. Это чем-то похоже на сложение скоростей в теории относительности. Еще один пример, термодинамика и понятие абсолютного нуля температуры. Остановив молекулы, атомы продолжают движение. Остановив атомы, кварки все еще двигаются и т.д. Погружение бесконечно.
Мы находимся между прошлым и будущим, между микро и макро миром. Во всех областях рано или поздно мы находим предел за который мы не сможем зайти и это нормально.
В математике все не так. Нам говорят что ноль — это число. Затем ставят его в один ряд со всеми остальными числами. Затем нам говорят, длина пути от минус единицы до единицы равна двум. И в этот момент наше сознание окончательно растворяет ноль среди остальных чисел.
Мы не можем делить на ноль, потому что забыли что однажды смешали понятие “ничто” и понятие “количество”.
Часть 2. Истина где-то рядом
В прошлой части мы расширяли алгебру и смогли делить на ноль арифметически. В качестве бонуса, способ оказался не единственным. Однако, все эти алгебры не дали ответа на вопрос: “Что там внутри или почему нам это не показывают?”
Пока древние вязали узелки, такой вопрос возникнуть не мог. Сейчас, куда не глянь, “бла-бла, для а≠0”. Значит ответ затаился где-то между узелками и настоящим. В математике все строго и последовательно, а значит и ответ не мог потеряться.

Мы попробуем приблизиться к ответу настолько близко насколько это возможно. Эта часть практически полностью посвящена философии арифметики. Скорее всего часть материала будет для Вас тривиальной. Однако у нас тут не повтор школьного курса арифметики.
Материал построен так, чтобы выделить структуру арифметики. Мы будем вгрызаться в нее с разных сторон и отрывать слои. Цель — понять, что на чем лежит.
2. Истина где-то рядом
2.1 Зачем вообще напрягаться?
Чтобы снова броситься в дебри, хотелось бы понять, почему этот вопрос периодически возникает и ради чего стоит искать ответ.
Давайте вспомним школьные годы, то время, когда нам впервые сказали: “На ноль делить нельзя, — вот так вот категорично. — Нельзя и все!”. А ведь до того в математике все было логично и последовательно. Складывали арбузы и вычитали дыни, яблоки перекатывали. Откуда не возьмись, на самом старте изучения математики, появился первый запретный плод.
Классический набор ответов только расстраивает
- «Нельзя и все!» или «Проверь на калькуляторе» — без комментариев. Особая педагогическая методика.
- «Яблоко можно разделить на двоих. Тебя и друга Колю. Можно на троих. А если на ноль человек делить, то сколько раз разрезать нужно?» — да, непонятно выходит. Да и вопросом на вопрос отвечать неприлично. А учитель-то для чего? Твердят что математика “красивая”, математика “царица”, а тут такой конфуз.
- “2∙0=0 и 3∙0=0, поделим оба равенства на ноль, то выходит что 2=0/0 и 3=0/0. Значит 2=3 что ли?” — пример, конечно, наглядный. Но такие примеры мало того что на вопрос ответа не дают, так еще и страх перед наукой сеют. А вдруг еще на что делить нельзя или умножать. А вдруг поскользнусь. А может учитель сам не разобрался?
- «Чтобы понять нужно много знаний. Это в ВУЗе изучают, и то не все» — ну да, а че делить то нельзя? До этого момента у нас причинно-следственные связи не нарушались, шли от простого к сложному. А ведь ноль — число как число. Деление — операция как операция. Запрет на ровном месте!
Но система образования не щадит никого (пруф). Нет другого выхода, кроме как идти дальше и осваивать новые знания. В голове происходит “скачок знаний”, как будто тысячелетие эволюции математики было пропущено. И это только начало.

"… не нужно проявлять лишней поспешности, нужно дать время ученику освоиться с тем внутренним переворотом, который в нем совершается в результате акта познания”, — Ф. Клейн, “Элементарная математика с точки зрения высшей”
В старших классах, откуда ни возьмись, появляются формулы окружности и треугольников, дискриминант, тригонометрические тождества и т.п. Что их объединяет? Все они пришли сверху, совершенно неизвестно откуда. Их нужно просто использовать, в худшем случае зазубрить.
Оказавшись в ВУЗе, большинство, вместо возвращения к пропущенному материалу, изучает «вышку» с уклоном в специальность. Объем формул, пришедших свыше, уже совершенно не смущает.
Да, систему образования понять можно. Специалисту платят за результат, а не за то что он знает откуда экспонента в его расчетах.
В итоге мы не приходим к выводам, так как это делают математики. В момент “скачка знаний”, то есть когда мы отбрасываем часть логических цепочек, вершится таинство. Мы принимаем на веру то что нам говорят. Учебник превращается в священное писание!

Запрет деления на ноль — это первый и самый навязчивый запрет математики. Поэтому он запоминается на всю жизнь. Это так же педагогическая проблема, которая оставляет отпечаток на всю математику, как на “тайну покрытую мраком”. Это сложная проблема, по сравнению с ней найти большинство пропущенных логических цепочек не составляет труда.
Превратить священное писание назад в учебник можно. Причина запрета должна стать строго определенной. Задача педагогов преподнести ее ясно. Наука не должна сеять сомнения.
2.2 Что такое деление?
Капитан Очевидность утверждает, чтобы поделить на ноль нужно знать что такое деление и что такое ноль. Как ни печально, гугл подсказывает, что многие адепты “магии деления на ноль” не проходят даже первый круг этого ада. А именно понять что они собираются сделать и с чем. Заглянем в Википедию:
Деле́ние (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению. Деление — это такая операция, которая считает сколько раз одно содержится в другом.Что из этого следует:
- Деление не самостоятельная операция. Она определяется через умножение. Если посмотреть на определение умножения, то оно определяется через сложение. Вычитание так же определено через сложение. Сложение самостоятельно и ни от кого не зависит.
- В определении нет упоминания о нуле. При повсеместном запрете деления на ноль это весьма странно. Кстати, упоминания нуля нет и в определениях остальных арифметических операций.
- Вторая часть определения не является частью определения, это всего лишь пояснение. Убедиться можно сравнив с аналогами в других проверенных источниках.

Похоже, самое полезное, что мы здесь нашли — это связь между операциями. Можно сказать что деление — вино третьего отжима, умножение и вычитание — второго, а сложение — первого. Возможно, именно по этой причине деление стало давать сбой при работе с нулем.
2.3 Порождающие операции
Итак, только операция сложения содержит правило о том, как по двум исходным аргументам (слагаемым) определить результат операции (сумму). Все остальные арифметические операции используют данное правило (соответствие чисел), но вдобавок накладывают свои “дополнительные условия”.

В зависимости от “дополнительных условий” арифметические операции можно поделить на прямые и обратные:
- Прямые операции: это сложение, умножение и возведение в степень. Выражая эти операции через сложение, все слагаемые остаются известны. Определение результата любой из операций не представляет сложностей.
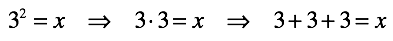
- Обратные операции: вычитание, деление, взятие корня (логарифмирование). Данные операции берут за основу соответствующую прямую операцию и “инвертируют” ее. Таким образом, выражая операцию через сложение, хотя бы одно из слагаемых оказывается неизвестно. Это слагаемое и есть результат операции. Сумма, как правило, известна.
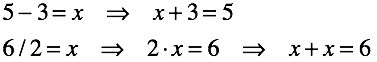
Определение результата операции, в общем случае, задача не тривиальная.

Все прямые операции обладают одним свойством. Они являются замкнутыми. То есть тип результата полностью определяется типами входных чисел (невозможно получить из произведения двух целых чисел дробный результат).
Обратные операции являются замкнутыми только частично (значение корня из целого числа может оказаться целым числом, а может и не оказаться). В тех случаях, где подобрать результат не удается операция оказывается не определена. Данную проблему издавна решают простым способом: рассматривают получившуюся запись операции и числа как новый тип чисел:
Таким образом, можно сказать что обратные операции и “порождают” новые типы чисел.
Математическим языком:
В общем случае использование термина “обратная операция” неприемлемо для обозначения способности операции порождать новые типы чисел. Например, “дополнительными условиями” можно:Деление одна из порождающих операций. Возможно, в процессе рождения что-то пошло не так и новорожденный получил травму. Для того чтобы ответить на это вопрос нужно понять откуда взялось деление и откуда взялся ноль.
- поместить результат операции в одно или несколько слагаемых (как показано на примере выше);
- определить результат операции как ответ на вопрос, сколько слагаемых участвовало в операции (дробные числа, иррациональные числа использующие корень);
- определить результат операции как сумму бесконечного количества слагаемых. При этом все слагаемые известны (число Пи и число Эйлера).
2.4 Эволюция арифметики
Попробуем структурировать наше представление об арифметических операциях и порождаемых ими типах чисел. Для наглядности представим один из вариантов, как может идти эволюция арифметики.
2.4.1 Область определения
Мы в пещере. С умением считать никто не родился. Однако в процессе “созерцания” появилось понимание, что такое понятие “количество”. То есть мы знаем что два мамонта и два яблока имеют нечто общее и можем это выразить, загибая пальцы. Соответственно ничего, кроме натуральных чисел на этом этапе мы не знаем.
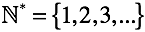
Множество натуральных чисел помечено звездочкой “*” для однозначности. Здесь и далее подчеркивается отсутствие понятия “ноль”.
Есть несколько формальных определений последовательности натуральных чисел. Мы возьмем за основу аксиомы Пеано. Примечательно что эти определения не были описаны древними. Они появились только в 19 веке, а после прошли процедуру уточнения (в первоначальном варианте их было девять, в современном виде уже пять).
Рассмотрим формальные определения и их суть в рамках нашей задачи (традиционное словесное описание можно найти на Википедии):
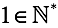
Есть число “один” и оно натурально.

Вводится функция следования S(x). Для всех натуральных аргументов она возвращает следующее за ним натуральное число. В первом приближении (весьма грубом) это S(x)=x+1, например 2=S(1) и 3=S(S(1)).
-

Вводится явный запрет на глобальную закольцованность порождаемой последовательности чисел. Генерируя числа мы не можем получить элемент с которого начали генерацию, то есть единицу.
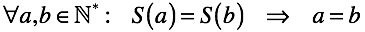
Разные аргументы функции следования должны давать разные результаты. Таким образом вводится явный запрет на локальную закольцованность. То есть функция следования не должна повторно сгенерировать число, которое уже было сгенерировано.
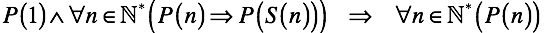
Математическая индукция, позволяющая подняться с уровня элементов последовательности до уровня последовательности в целом. Если какое-то высказывание “P” верно для единицы и для каждой пары соседних элементов, то оно верно и для всех элементов последовательности.
Например. Для чисел 2 и 3, верно что между ними есть один средний элемент 2.5, для 3 и 4 это 3.5 и т.д. Делаем вывод, между любыми соседними натуральными числами есть средний элемент и он единственный.
Какой вывод можно сделать из этих аксиом? Вводится запрет на закольцованность в любом виде (глобальную или локальную). Запрет на закольцованность всегда требует наличие следующего элемента. Так появляется математическое понятие “бесконечность” основанное на понятии «количество”. Понятие “бесконечность” не может существовать без понятия „количество”.
Математическим языком:
Довольно часто за “стартовый элемент” в аксиомах Пиано берут ноль. Почему так делать нельзя, будет раскрыто при описании операции “вычитание” (уже совсем скоро).
Функция следования не использует операцию сложения в прямом смысле этого слова. Это фундаментальная функция, которая используется как для построения множества натуральных чисел, так и для формального определения операции сложения.
То есть и числа и арифметические операции определены при помощи функции следования.
Функция следования входит в класс примитивно рекурсивных функций, рассматриваемых в теории алгоритмов. Как известно, понятие рекурсия не содержит требования ее конечности (достижимости терминальных ветвей), а значит она так же неявно определяет понятие “бесконечность”.
2.4.2 Сложение
Первая операция, возникшая в ходе нашей эволюции. Как целые пальцы не загибай, результат будет целым. Разве что у вождя сумма пальцев может быть чуть больше чем у всех остальных. Если пальцев не хватает, всегда можно позвать научного ассистента по пещере и расширить разрядную сетку.

2.4.2 Вычитание
В четверг охотники подстрелили 12 мамонтов. За пятницу съели 5 штук. Сколько мамонтов осталось?

Задача хорошо решается путем введения разгибания пальцев. Но подход работает не всегда. Например, чтобы оценить запасы на выходные охотник загибает семь пальцев за остаток, разгибает пять пальцев за субботу (норма расхода в день) и “пытается” разжать за воскресенье.
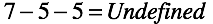
В этот момент между “try” и “catch” возникает ArithmeticException. Результат оказывается не определен. Наша операция определена только для случая, когда уменьшаемое больше вычитаемого.

Однако определение вычитания не накладывает никаких ограничений. Чтобы избавиться от требования “a > b” введем “правило перестановки”. То есть позволим менять местами уменьшаемое и вычитаемое. Но чтобы тождество оставалось верным результат нужно пометить каким-то маркером, например знаком “минус”. Всякие маркеры для математики — дело обычное (например, признак отсутствия нуля у
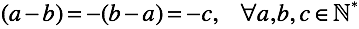
За счет вспомогательной операции “перестановки” мы подошли к первой абстракции — “отрицательные числа”. Пометка в виде знака “минус” у натурального числа есть ничто иное как признак отложенного вычитания (но это только пока).
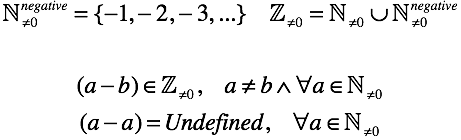
У нас остался всего один не определенный случай, когда уменьшаемое и вычитаемое равны. Если мы захотим определить его, то нам придется ответить на вопрос что такое понятие “ничто”. Хотя к чему все эти сложности, обозначим “ничто” символом “0” (позже вникнем по полной).

Осталось зафиксировать наше решение в виде “правил сложения/вычитания нуля”. Они следуют из определения нуля после пары нехитрых перестановок:
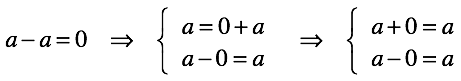
Посмотрим, насколько хорошо работают введенные правила. Решая уравнения, мы по двум известным числам всегда можем найти неизвестное третье. Совершенно неважно в какой части уравнения оно стоит, решение всегда однозначно.
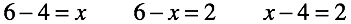
Отрицательные числа появились в результате перестановки, ноль же заполнил “ничто”. Отрицательные числа и ноль рождены разными способами. Далее мы будем рассматривать две ветви эволюции: отдельно всех чисел без нуля и отдельно ноль.
2.4.3 Умножение
Умножение по определению является сокращенной записью сложения. Умножая натуральные числа, результат может быть только натуральным. На этом этапе эволюции для нас польза от определения заканчивается.

Для отрицательных чисел в определении нет ни слова о том как их перемножать. Эти правила сформировались постепенно в ходе решения прикладных задач. В современной трактовке они известны как дополнение к умножению в виде “правил знаков”. Они определены настолько хорошо, что применяя их к целым не нулевым числам, операция остается замкнутой.
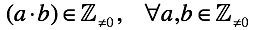
В случае нуля ситуация отличается кардинально. Вводится еще одно правило “правило умножения нуля“ (умножение любого числа на ноль дает ноль). Но новым это правило только кажется. Ввести какое либо иное правило мы не можем. Определение умножения жестко связывает нас со сложением. Раскрывая умножение через сложение, мы используем “правила сложения/вычитания нуля”, соответственно ничего кроме нуля мы получить не можем.

Математическим языком:
Если сравнить операции сложения и умножения в арифметике и общей алгебре, то можно заметить одно серьезное различие. В арифметике данные операции связаны по определению. Дистрибутивный закон является следствием этих определений. В общей алгебре наоборот, операции описываются независимо друг от друга, а уже в определении поля (кольца, если говорить точнее) связываются дистрибутивным законом. Как следствие:
Поле, венец универсальности, “за уши” притянуто к элементарной арифметике. Но чтобы избавиться от этой подпорки (описать требования к операциям симметрично) придется расширить определение дистрибутивного закона (начиная с кольца конечно). Есть основания полагать, что венцом универсальности может стать другая алгебраическая система, для которой поле окажется частным случаем.
- В определении поля есть требование к обратному элементу. При этом для умножения и для сложения требование описано не симметрично. Допускается отсутствие обратного элемента по умножению для нейтральных элементов по сложению, но не наоборот.
- Для придания симметрии при описании колес пришлось отказаться от привычного дистрибутивного закона, а значит и от оперирования полем.
2.4.4 Деление
Деление — операция обратная умножению. В уравнениях с положительными и отрицательными числами появляется возможность подстановки не кратных чисел.
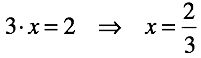
Как следствие операция порождает “рациональные числа”.
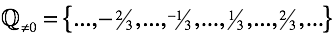
Чтобы вписать их в арифметику, в комплекте идут “правила действий с обыкновенными дробями”. К счастью, эти правила гармонично сосуществуют с введенными нами ранее “правилами знаков”. В итоге в уравнениях сохраняется возможность определить по двум известным числам неизвестное при любой расстановке.

В случае нуля его можно умножать на рациональные числа. На этом всё, гармония закончилась! Только для двух из трех видов уравнений с произвольными числами решение может быть найдено.
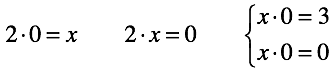

Во-первых, появилась возможность составить уравнение с настолько не удобными числами, что мы не сможем подобрать ни одного решения. Решение “не возможно”.
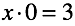
Во-вторых, появилась возможность составить уравнение в котором есть бесконечное множество решений. Выбрать какое-то одно из них так же невозможно. Решение “не однозначно”.
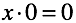
Несложно догадаться, корень проблемы деления на ноль лежит в “невозможности” и “неоднозначности” умножения нуля. Умножение, в свою очередь, ретранслирует “правила сложения/вычитания нуля”. По сути можно задать уравнения, обладающие такими же свойствами, используя только сложение.
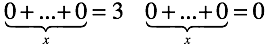
В обоих уравнениях нужно определить количество нулей, которые нужно сложить чтобы получить произвольное число или ноль.
Деление не привнесло чего-то качественно нового. Произошла трансформация “невозможности” и “неоднозначности” сложения в конкретные сущности, в неопределенности вида 1/0 и 0/0 соответственно.

Получается что деление, как первый подозреваемый, не виновато в том что на ноль делить нельзя.

Пока не существует понятия “ноль” все операции, включая возведение в степень и взятие корня (логарифмирование), хорошо замкнуты (уже правда на комплексных числах) и арифметика работает великолепно. Но есть одно “но”, при такой конфигурации арифметики операция вычитания, оказывается определена не полностью.
После введения нуля сложение и вычитание неплохо работает. Для остальных операций он скорее повод для установки костылей (
2.5 Что такое ноль?
Итак, раз операция деления оказалась не виновата в запрете деления на ноль. Попробуем тогда собрать воедино все, что мы знаем о нуле:
- Потребность в нуле появилась при определении операции вычитания.
- Для разрешения большей части неопределенностей вычитания было введено “правило перестановки”. Знак минус перед числом, по сути, является маркером “отложенного вычитания”. Все что “правило перестановки” не осилило, закрыл собой ноль. По сути, ноль был введен для обозначения понятия “ничто”.
В предыдущей части статьи (при проективном расширении числовой прямой) мы “с потолка” ввели беззнаковую бесконечность. Ноль, аналогичная “затычка” для всего, что нам не понятно. Последствия, в виде появления новых неопределенностей, оказываются весьма предсказуемы.
- У понятия “ничто”, отсутствует связь с понятием “количество” (основа для определения натуральных чисел и сложения). Эти понятия существуют сами по себе и мы можем “созерцать” их совершенно независимо, например “пять яблок” и “вакуум”. Отсюда следует, что в своей сути ноль так же не связан с натуральными числами, как понятие “ничто” не связанно с понятием “количество”.
Вычитание использует данное понятие, но не порождает его.
Отсутствие породившей операции качественно отличает ноль от всех остальных чисел.
Для того, чтобы была ясна связь не рассмотренных нами типов чисел с операциями, продолжим, максимально кратко, тему эволюции. Мы остановились на делении. Комплексные числа и часть иррациональных порождаются операцией взятия корня (логарифмированием) над отрицательным числом. Прочие иррациональные (число Пи и число Эйлера) появляются за счет введения бесконечных сумм и бесконечных умножений. Мнимые единицы кватернионов даны по определению и не выведены арифметически. Соответственно, инородны в рамках эволюции чисел.
- Вероятно именно из-за возможности одновременного “созерцания” понятия “ничто” и понятия “количество” ноль иногда приписывают к натуральным числам. Однако гораздо более логичным видится вынесение нуля как минимум в отдельный тип чисел.
- Было принято, что ноль единый и абсолютный. Именно из этого, весьма спорного, предположения следуют “правила сложения/вычитания нуля” с другими числами. Как следствие, ноль обладает уникальным свойством, которое отсутствует у всех остальных чисел. В результате сложения нуля с произвольным числом неизвестно, сколько нулей участвовало в операции и были ли они вообще.
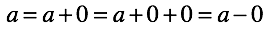
На последнем пункте стоит остановиться поподробнее. Попробуем представить не абсолютный ноль.
Допустим, у нас есть мамонт. Для его перевозки нужна тара. Если положить мамонта в тару, а потом вытащить, то в таре окажется “ничто” (прям как на картинке со спичкой выше). Однако тара для двух мамонтов несколько отличается от тары для одного. В случае кражи есть основание выставлять обвинение в соответствии с размером оставшейся тары. А значит, существуют ситуации когда одно “ничто” другому “ничто” рознь.

Может ли “ничто” быть разным или “ничто” есть единая и абсолютная сущность? Это вопрос на который невозможно дать ответ. Аналогичен и бессмысленен спор на тему есть ли Бог, а и есть то единый он или их много. Ответа на этом свете мы не узнаем.
Математическим языком:
Отношение математики к нулю как к единому и абсолютному объекту лучше описать по отдельным разделам математики:Таким образом, на самом дне арифметики, там где не существует ни натуральных чисел, ни сложения (а значит и прочих операций), существует ноль.
- Общая алгебра. В алгебраических системах с разрешенным делением на ноль, очень ярко проявляется борьба с абсолютным нулем. Причудливые операции вычитания это не прихоть, а следствие уничтожения единого и абсолютного нуля. Например, в колесах для вычитания определено следующее тождество:
- Математическая логика. Формально арифметика определяется расширением аксиом Пеано. Пять аксиом, определяющие ряд натуральных чисел, дополняются еще четырьмя. Это расширение определяет связь базовых арифметических операций (сложение и умножение) с числами:
В этих аксиомах заложено особое отношение к нулю. Формально определяется объект со свойствами отличными от всех остальных чисел. Этому объекту посвящено две из девяти аксиом описывающих всю арифметику.
Здесь мы прикасаемся к одному из проявлений теоремы Гёделя о неполноте. Невозможно средствами арифметики доказать или опровергнуть единую или множественную сущность нуля.
- Теория алгоритмов. Можно заглянуть в арифметику еще глубже. Для построения последовательности натуральных чисел и определения операции сложения, используется класс примитивно рекурсивных функций. Функция следования S(x), используемся в аксиомах Пеано, одна из них. Наравне с ней определена Нулевая функция O(x), функция которая всегда возвращает ноль.

Хорошо, ответа на вопрос сколько должно быть нулей арифметика дать не может. Мы пользуемся одним нулем. В колесах, рассмотренных в первой части, использовалась арифметика с бесконечным количеством нулей. А может ли быть конечное число нулей, но больше одного.
Может и такие арифметики успешно используются. Один из ярких примеров арифметика со “знаковым нулем”, реализованная в JavaScript.
Математическим языком:
Знаковый ноль, хоть записывается аналогично +0 и -0, не имеет ничего общего с исчислением бесконечно малых.Однако и эта арифметика грешит неопределенностями.
Введение знакового нуля является еще одним вариантом расширения числовой прямой. В общей топологии существует очень близкое (но не тождественное) пространство “линия с двумя началами” (не хаусдорфово).
Пример работы JavaScript
console.log(+0) => 0
console.log(-0) => -0
console.log(-0 === +0) => true
console.log(0-0) => 0
console.log(-0-0) => -0
console.log(0/0) => NaN
console.log(-0/0) => NaN
console.log(-0/-0) => NaN
console.log(Infinity/Infinity) => NaN
console.log(-Infinity/Infinity) => NaN
console.log(-Infinity/-Infinity) => NaN
console.log(Infinity — Infinity) => NaN
console.log(Infinity + Infinity) => InfinityМожно сделать вывод, что неопределенности в арифметике будут сохраняться до тех пор, пока количество нулей конечно.
По большому счету неважно как мы будем относиться к нулю. Нужен ли нам единый и абсолютный ноль, а может парочка или вообще бесконечное количество, арифметика всегда сможет под нас подстроиться.

2.6 Бесконечность наше всё
Напоследок, хотелось бы представить хотя бы один вариант числовой оси содержащей бесконечное количество нулей (данный пример описывает концепцию и не претендует на математическую строгость).
Для вычитания, когда уменьшаемое и вычитаемое равны, вместо ввода нуля определим операцию “сокращения”. То есть разрешаем вычеркивать эквивалентные выражения с противоположным знаком. Но если мы сократили все, то результат уже не пригоден к дальнейшему использованию.
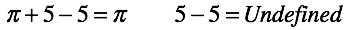
Отсчет в числовой оси начнем с единицы (от первого числа зародившего понятие “количество”). Для генерации остальных чисел воспользуемся бесконечной последовательностью, определенной функцией следования (она же использована в аксиомах Пеано). Это будет наш эталонный генератор бесконечной последовательности.
Чтобы получить очень маленькое число при помощи функции следования нужно затратить столько же сил сколько и на генерацию очень большого. Используем функции f(x)=1/x и f(x)=x. Приводить в десятичный вид рациональную дробь задача не стоит, соответственно вычислительная сложность функций одинакова.
Так как ни “абсолютный ноль“ (отмечен символом ноль), ни »потенциальная бесконечность" (отмечена символом беззнаковой бесконечности) недостижимы, ось растет из единицы бесконечно в обоих направлениях (масштаб неравномерный).

При определении вычитания определено “правило перестановки”. Мы же, в свою очередь, делаем копию нашей прямой и отображаем ее зеркально. Числа-близнецы и недостижимые для них пределы помечаем знаком “минус”. Положительная прямая, не соединена с отрицательной. Переход из одной прямой в другую выполняется только за счет “правила перестановки”.

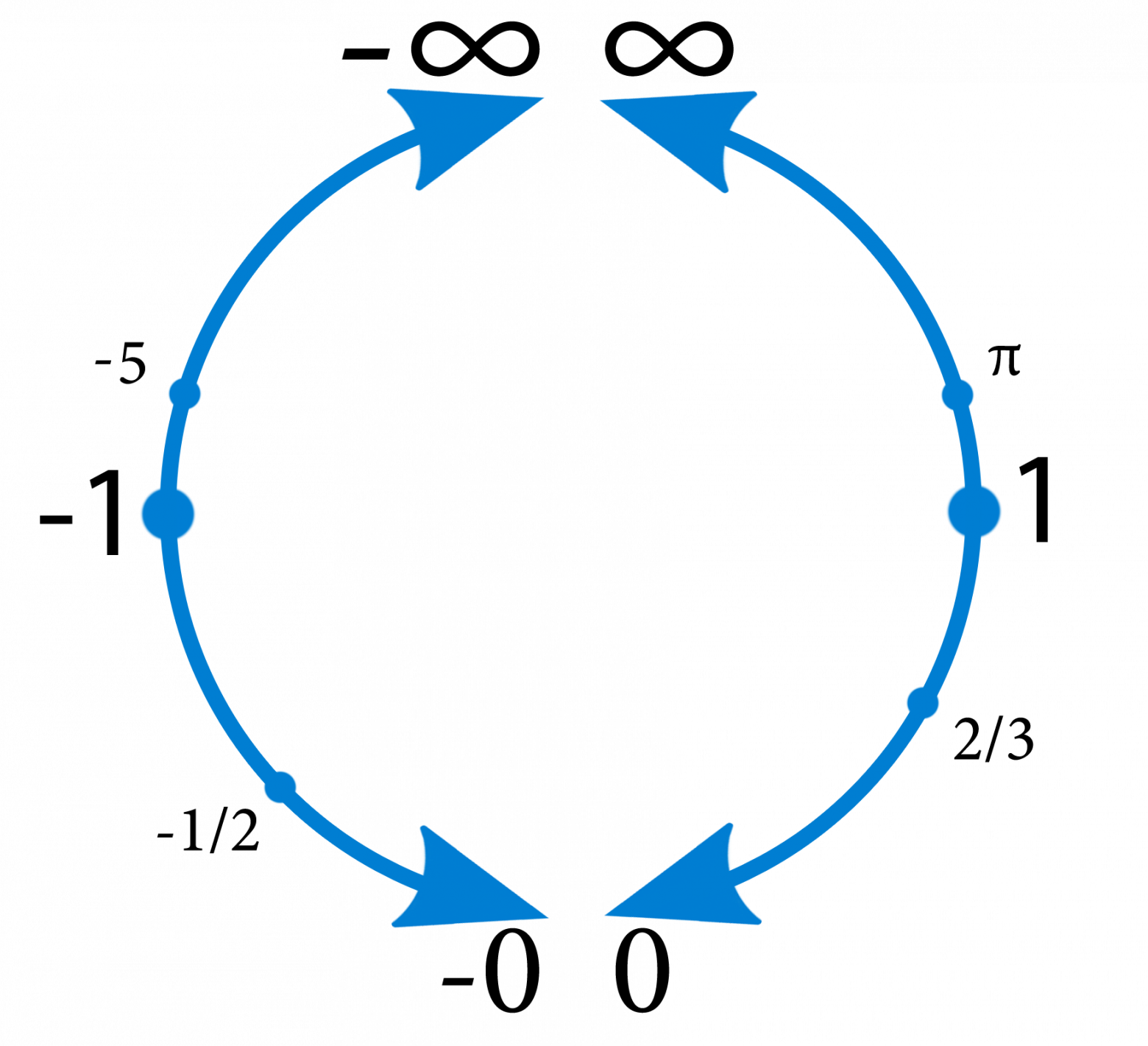
Для наглядности изобразим полученную числовую прямую в виде круга. Так же, как мы делали при проективном расширении. Однако, предельные значения не смыкаем (компактификацию не выполняем). Данная трансформация смысловой нагрузки не несет и выполнена только для улучшения восприятия.

Теперь мы готовы к самому главному. Выполним переход от единой потенциальной бесконечности к бесконечному множеству актуальных бесконечностей (аналогичный подход используется в нестандартном анализе).
Будем относится к бесконечно большим величинам как к полноправным числам. За эталонную актуальную бесконечность возьмем “скорость” с которой функция следования достигает любого произвольного числа. Обозначим это число
Для получения различных актуальных бесконечностей будем использовать понятие предела функции при стремлении к числу
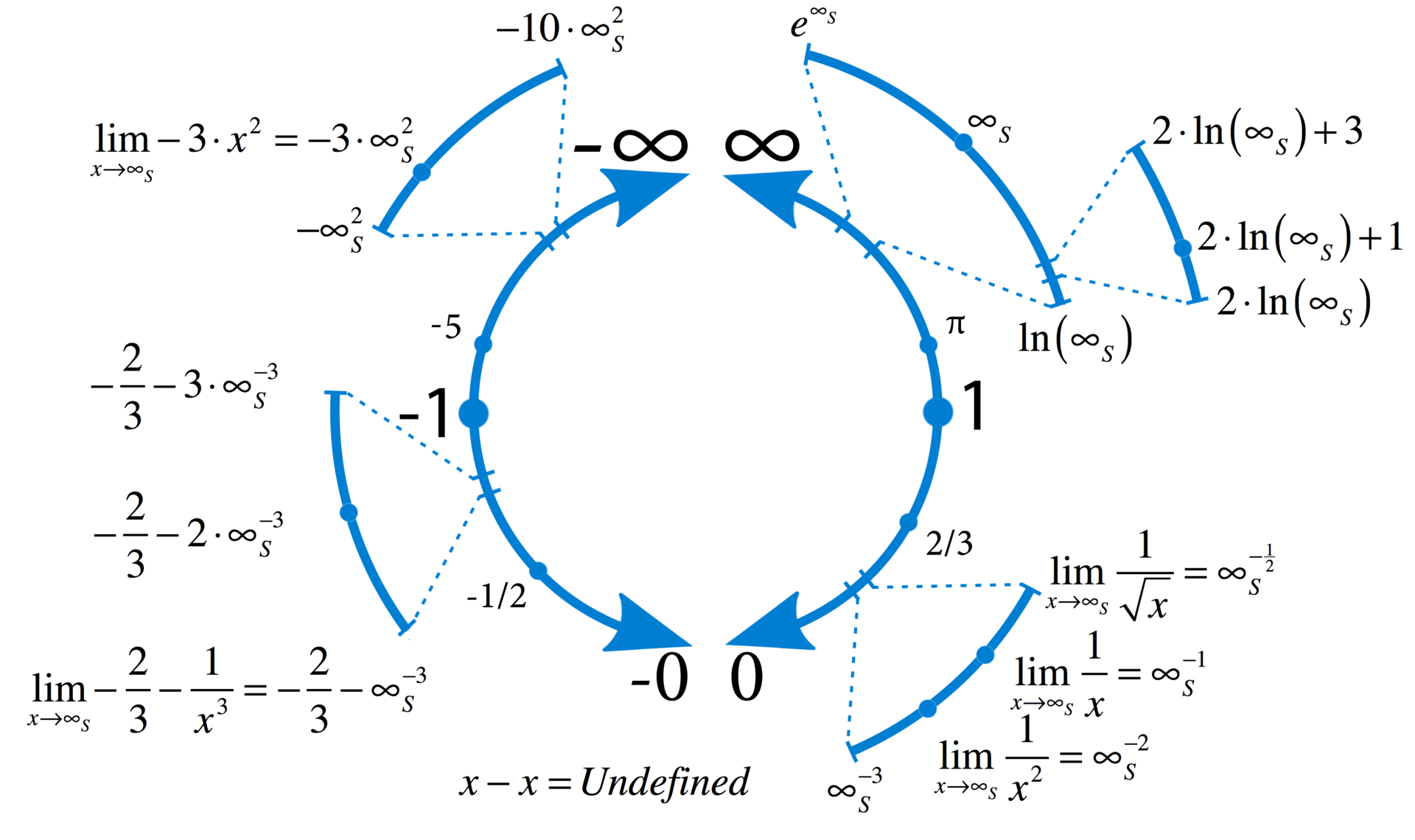
Возводя число
Математическим языком:
С точки зрения общей алгебры, наша алгебраическая система, не является полем, так как отсутствует ноль (нейтральный элемент). Нестандартный анализ оперирует аналогичными актуальными бесконечностями, они называются гиперреальными числами. Ноль (нейтральный элемент) является одним из гиперреальных чисел. Соответственно алгебраическая система нестандартного анализа оперирует полем.
Наша эталонная бесконечностьпредставляет собой одно из чисел нестандартного анализа. Однако, вместо упрощенного понятия “скорость”, в нестандартном анализе числами являются классы эквивалентности бесконечных последовательностей. Так как в нашем концепте все алгебраические операции можно выразить через функцию следования, значит любую актуальную бесконечность, образованную арифметически, можно выразить через
.
По факту пределы практически перестают упрощаться, в том виде к которому мы привыкли. Сейчас мы просто производим замену переменной на. Правило Лопиталя так же не применимо. В первой части было показано как в классике, при определении производной, отбрасывается бесконечно малая величина. Однако стоит отметить, понятие предела в нестандартном анализе все же существует, но определено несколько шире.
Если возникнет практическая необходимость, можно определить операцию вычитания и для равных чисел (вместо “сокращения” определенного нами выше). Например, это может быть число низшего порядка, нежели исходные числа
Эпилог
Мы находимся между прошлым и будущим, между микро и макро миром. Во всех областях рано или поздно мы находим предел за который мы не сможем зайти и это нормально.
В математике все не так. Нам говорят что ноль — это число. Затем ставят его в один ряд со всеми остальными числами. Затем нам говорят, длина пути от минус единицы до единицы равна двум. И в этот момент наше сознание окончательно растворяет ноль среди остальных чисел.
Мы не можем делить на ноль, потому что забыли что однажды смешали понятие “ничто” и понятие “количество”.
Полезная литература
- Ф.Клейн: Элементарная математика с точки зрения высшей (pdf)
- В.А.Успенский: Что такое нестандартный анализ? (pdf)
- Setzer, Anton (Drafts): Wheels, 1997 (pdf)
- J.J.O’Connor and E.F.Robertson: A history of Zero (html)
- Ю.Лебедев: Математика бесконечности (html)
- http://en.wikipedia.org/wiki/Undefined_(mathematics)
- https://ru.wikipedia.org/wiki/Нестандартный_анализ