
Примечание переводчика: я заменил оригинальные обозначения сторон монеты head/tail на аверс/реверс, чтобы не вносить путаницу русскоязычными орёл/решка. На иллюстрации выше слева аверс (head), справа реверс (tail).
Спасение невозможно?
Это одна из тех типичных загадок о заключённых, в которых вы приговорены к смерти и можете спастись, только если докажете свои умственные способности тюремщику. Вы и ваш друг были заключены в тюрьму. Ваш тюремщик предлагает вам испытание. Если вы его выполните, вы оба будете освобождены.
Правила:
- Тюремщик отводит вас в отдельную камеру. В камере находятся шахматная доска и банка с 64 монетами.
- Тюремщик берёт монеты по одной и кладёт их на каждую клетку доски. Он помещает монеты произвольно — некоторые будут обращены вверх аверсом, некоторые — реверсом (или все будут аверсом, или реверсом, вы понятия не имеете, всё на усмотрение тюремщика). Если вы попытаетесь вмешаться в процесс раскладки монет, это повлечёт немедленную смерть. Если вы попытаетесь принудить, посоветовать или убедить тюремщика любым способом — немедленная смерть. Вы можете только смотреть.
- Когда все монеты будут разложены, тюремщик укажет на одну из клеток и скажет: «Эта!» Указанная клетка — «магическая» — ваш ключ к свободе.
- Тюремщик разрешит вам перевернуть одну монету на доске. Только одну, но это может быть любая монета на ваш выбор. Это единственное изменение, которое вам разрешено сделать в раскладке тюремщика.
- Затем вы будете выведены из комнаты. Если вы попытаетесь оставить какие-либо сообщения или подсказки для вашего друга… да, вы угадали, немедленная смерть!
- Тюремщик приведёт вашего друга в комнату.
- Ваш друг должен будет осмотреть доску (трогать запрещено) и решить, где, на его взгляд, расположена «магическая» клетка.
- У него только одна попытка. Исходя из расположения монет, он должен указать на клетку и сказать: «Эта!»
- Если он укажет верно, вы оба будете помилованы и немедленно освобождены. Если неверно — вас обоих казнят.
- Тюремщик объясняет эти правила вам обоим заранее и даёт время посовещаться, чтобы разработать стратегию.
Возможно ли разработать стратегию?
На первый взгляд, эту задачу невозможно решить. Мы не можем влиять на тюремщика, раскладка монет может быть любая, и мы понятия не имеем, на какую клетку тюремщик укажет (фактически, он сам, возможно, не знает, какую клетку выберет).
64 клетки, на которые он может указать. 26 возможных ответов. Нам нужно 6 битов информации, чтобы точно идентифицировать клетку. Если вы переворачиваете монету, это один бит информации. Поскольку мы не можем передать состояние доски «до», у нашего друга нет возможности указать, какая монеты была перевёрнута. Подумайте, если друг входит в комнату и видит 63 аверса и 1 реверс, он не может знать, что единственный реверс — это монета, которые вы перевернули, или перед вами была доска с 62 аверсами и 2 реверсами, и вы перевернули один реверс!
Возможно ли передать 6 битов информации переворачиванием одной монеты?
Есть стратегия, позволяющая вам спастись со 100% вероятностью независимо от раскладки монет и положения «магической» клетки. Решение не подразумевает какого-либо мошенничества или уловок, оно чисто математическое.
Начало
Задачу можно решить, поскольку фактически у нас есть больше информации, чем один бит, передаваемый между вами и вашим другом. Расположение остальных монет хранит информацию, и мы можем это использовать. На самом деле у нас есть достаточное количество (шесть) управляемых битов в раскладке монет, с помощью которых мы можем идентифицировать любую клетку на доске.
Две клетки
Представьте, что у нас доска всего c двумя клетками. Есть 4 возможных варианта расположения монет (А — аверс, Р — реверс): РР, АА, РА, АР.

Тюремщик может выбрать в качестве «магической» как первую клетку, так и вторую.
Заранее мы договариваемся об одном правиле — если тюремщик указывает на первую клетку (белую), то необходимо сделать так, чтобы на первой клетке был аверс. Возможные варианты:
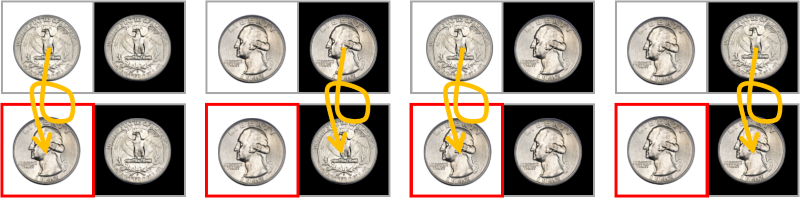
Если раскладка была РР, я могу перевернуть первую монету аверсом, если АА — я переверну вторую монету, так как первая уже повёрнута аверсом (по нашему правилу это ничего не изменит, но я должен перевернуть монету).
Во всех вариантах выше на первой клетке оказался аверс. Согласно нашему правилу, это означает, что тюремщик выбрал первую клетку.
Аналогично, если тюремщик укажет на вторую клетку, я сделаю так, чтобы на первой клетке был НЕ аверс. Это подсказка моему другу, что «магическая» клетка — не первая.

Во всех вариантах на первой клетке не аверс. По нашему правилу это означает, что тюремщик выбрал вторую клетку.
Проблема решена!
Индукция
Математики (и некоторые программисты) скажут вам, что это всё, что нам нужно, чтобы доказать, что решение задачи возможно. Если мы можем закодировать один бит информации, используя две клетки, то с помощью математической индукции мы можем подтвердить, что возможно закодировать 2 бита в 4 клетах, 3 — в 8 … 6 битов — в 64 клетках.
Двоичное представление
Если мы промаркируем клетки от 0 (верхняя левая) до 63 (нижняя правая) в двоичном представлении, мы сможем отобразить, частью какого вложенного множества каждая клетка является.
В оригинале статьи размещено интерактивное изображение доски. Число в нижнем левом углу отображает номер клетки в двоичной записи. Каждая цифра представляет множество, к которому клетка относится. Единица в любой позиции показывает, что клетка находится в одной половине множества, ноль — в другой. По определению каждая клетка уникальна и имеет индивидуальный набор битов.
Чётность
Вместо использования двух клеток как в простом примере выше мы разделим доску на различные комбинации двух множеств. Применим к этим двум регионам/множествам то же правило маркировки, что и с одиночными клетками — будем обозначать, в первом или втором регионе находится «магическая» клетка.
Поскольку регионы являются коллекциями клеток, мы не можем просто повернуть все монеты в регионе аверсом. Вместо этого мы перевернём одну монету. Мы можем посчитать количество аверсов в регионе — если их число будет нечётным, примем это за единицу, если чётным — ноль. Переворачивание одной монеты в регионе изменит число аверсов с нечётного на чётное, и наоборот (прибавление/вычитание единицы к любому числу инвертирует его чётность/нечётность).
Таково понятие чётности. Переключение из одного состояния в другое прибавлением или вычитанием одного бита широко используется в компьютерах.
Чтобы изменить чётность региона, нам достаточно перевернуть одну монету в нём.
Используя маски степеней двойки, мы можем разделить доску на регионы несколькими способами. Ниже изображены различные способы разделения доски, основанные на состоянии битов (степени двойки) в номере клетки. Совмещение этих фильтров позволяет определить одну клетку, которую можно перевернуть, чтобы изменить чётность любого/всех битов.

20 эквивалентно логическому «И» (AND) с 000001, 21 — 000010 … 25 — 100000.
По определению, каждая клетка имеет уникальный набор битов. Мы можем перевернуть одну монету, чтобы изменить чётность любой комбинации этих фильтров.
Раскладка, созданная тюремщиком, имеет собственную (естественную) чётность. Монеты расположены произвольным образом, и мы можем посчитать чётность (количество аверсов) в каждом регионе. Комбинация этих битов чётности даст нам случайное шестибитное число.
Для идентификации «магической» клетки нам необходимо как раз шесть битов, и мы можем закодировать их с помощью чётности. Мы знаем, что можем перевернуть одну любую монету, и это приведёт к изменению одного/нескольких битов числа. Всё, что нам нужно — найти нужную монету, переворачивание которой изменит комбинацию битов чётности таким образом, чтобы получилось необходимое число (двоичная запись номера «магической» клетки).
Всё вместе
Тут я снова отправляю читателей к интерактивной модели в статье-оригинале.

На левой доске можно выбрать расположение «магической» клетки. Внизу справа указан номер выбранной клетки (Target=…), слева — его двоичное представление.
Доска справа показывает раскладку монет. Изображены только аверсы (из соображений наглядности), реверсы обозначены пустыми клетками. Кнопка «Random» заполняет доску новым случайным набором монет. Кнопка «Clear» переворачивает все монеты реверсом.
Под правой доской серым цветом слева обозначена собственная чётность доски, зелёным справа — номер монеты, которую надо перевернуть. Слева под собственной чётностью это же число записано в двоичном виде.
Откуда эти значения?
Мы уже знаем, откуда взялось число под левой доской. Это просто двоичное описание клетки, каждый бит числа показывает, присутствует или нет эта монета в фильтрах-степенях двойки, изображённых выше.
Серое число под правой доской показывает собственную чётность доски. Для каждого фильтра мы находим, чётное или нечётное число аверсов расположено в этом регионе. Единица в любом разряде числа говорит о том, что в этом регионе нечётное число аверсов.
Зелёное число показывает номер той клетки, состояние которой нужно изменить (перевернуть монету), чтобы чётность доски соответствовала желаемому номеру «магической» клетки. Оно вычисляется выполнением битовой операции исключающее «ИЛИ» (XOR) над собственной чётностью доски и желаемым значением.
Исключающее «ИЛИ»
Оператор XOR широко используется в программировании. У него несколько интересных свойств. Если исключающее «ИЛИ» применить дважды с одним и тем же значением, он вернёт исходное состояние:
(A XOR B) XOR B = A
Также, если мы применим XOR к какому-либо числу и полному набору битов (числу, состоящему из одних единиц), все биты исходного числа будут инвертированы. Применение XOR к числу и какому-то набору (установленных) битов инвертирует в исходном числе эти биты и сохраняет состояние остальных.
Именно поэтому мы использовали оператор XOR для вычисления положения монеты. Для каждого бита чётности, независимо от того, содержит он уже верное значение, и мы хотим его сохранить (XOR c 0), или мы хотим переключить его (XOR c 1).
Пример:
Если номер «магической» клетки 101001 (41) и собственная чётность доски 010101, то нам нужно перевернуть монету в клетке 111100 (60):

Также вы можете использовать XOR, чтобы быстро посчитать собственную чётность доски. Для этого нужно один раз обойти всю доску и провести эту операцию над каждым значением (порядковым номером) клетки с аверсом.