Все события и имена вымышленные
Часть вещей, которые я взял с собой на смену
Я думал, что я самый безбашенный человек в лагере, пока не приехал преподаватель Яндекса. Босиком. Он отпил глоток воды из графина и сказал: «Эээх, раньше я так водку пил». Затем он прочитал искрометную лекцию и «нарисовал» множество эллиптических кривых.
Вот как Алексей Савватеев анонсировал свою лекцию:
В журнале «Квант» номер 8 за 1983 год в статье «Вокруг биссектрисы» на странице 36 И.Ф.Шарыгин формулирует такую задачу:
«Про данный треугольник известно, что треугольник, образованный основаниями его биссектрис — равнобедренный. Можно ли утверждать, что и данный треугольник равнобедренный?»
Ответ отрицательный, но в статье далее сказано:
«К сожалению, автор не сумел построить конкретный пример треугольника (то есть точно указать величины всех его углов или длины сторон) со столь экзотическим свойством. Может быть, это удастся сделать читателям журнала?»
С тех пор построены три примера. Последний пример выводит нас на теорию эллиптических кривых и операцию сложения точек.
В лекции мы построим ЦЕЛОЧИСЛЕННЫЙ треугольник, обладающий требуемым свойством. Вопрос о бесконечности таких треугольников пока ещё остаётся открытым. Школьная задача, таким образом, приведёт нас в самое сердце одной из красивейших ветвей современной математики.
Смена в самом разгаре, кое-что интересное мы уже успели сделать, а что-то еще в планах.
В лагере есть обязательные лекции, есть приезжающие лекторы, есть воркшопы, есть самостоятельная работа над проектом. Самое интересное происходитпосле отбоя на переменах и между мероприятиями. Вот там-то я и веду свою партизанскую деятельность.
Начал я с самого простого: чтобы в чем-то разобраться, надо это что-то разобрать. В этот раз на растерзание просится радар-детектор (не путать с антирадаром). Вслед за мной ребята разобрали два ноутбука, типа починить. (И нашли внутри одного из них линейку и таблицу перерасчета разных величин.)
Прошлые распилы: распил лазера, распил электрошокера, распил фонарика

Разберемся, что такое Ка и Кu диапазоны, что такое эффект Допплера, что такое рупорная антенна, как работает полицейский радар и лидар, как глушится радиосигнал и что такое лазерный джаммер.

Написал я письмецо Крису Бурму, чтобы он ответил на пару вопросов и вдохновил на подвиги юных гемдизайнеров. Посмотрим, что он ответит.
В России выпущены несколько игр, но игру с самым интересным геймплеем (на мой взгляд) предали забвению. Мне захотелось реконструировать сей шедевр и подать хоть один конструктивный пример ребятам. (А то все распил, да взломы).

GIPF (1998) – игра смещения, TAMSK (1998) – игра давления, ZÈRTZ (2000) – игра пожертвований, DVONN (2001) – игра мобильности, YINSH (2003) – игра перемен, PÜNCT (2005) – игра соединения, TZAAR (2007) — игра баланса.
Первый прототип

Работа продолжается, а вожатые и дети выстроились в очередь, чтоб поиграть в нее. Надеюсь, до конца смены успею. Жаль, что есть баг: в часах разное количество песка, погрешность по времени до 20%.

В 2004 году немецкие ученые из университета в Оснабрюке во главе с Питером Кёнигом успешно провели эксперимент по внедрению человеку нового чувства. Участники эксперимента полтора месяца носили массивный пояс с электронным компасом, датчики которого вибрировали, будучи направленными на север. Они, подобно птицам, научились чувствовать магнитное поле земли и вот как пытались описать свои ощущения: «Я интуитивно ощущал направление к моему дому или офису. Я мог стоять в очереди в кафе и вдруг подумать: я живу вон там». Или: «В течение первых двух недель мне надо было концентрироваться. Затем все происходило интуитивно. Я мог даже представить расположение мест и помещений, где я когда-то был».

Исходный код для проекта

Пояс немецких коллег

Вот из этого мы будем паять свой пояс всевластия
Видео про встраивание в мозг новых чувств
http://www.youtube.com/watch?v=lmYyhuN0S2c
Есть много мифов о том, как наручники взламывают фантиками и зубочистками, ломают цепь руками.
Попробуем развенчать мифы про взлом наручников и рассмотрим все фичи и баги нормальных наручников, которые есть в любом интернет-магазине.
Хакеры взламывают наручники на DefCon
Сижу, ковыряюсь шпилькой в наручниках и тут в домик постучался вежливый мужчина в галстуке и представился службой безопасности коттеджного поселка. Я немного побледнел. Но оказалось, его интересовал вопрос, не выкорчует ли мой слэклайн его любимую елочку.

Препод рассказал про игрули, Симпсонов и Гриффинов с точки зрения дизайна

Слушали очень внимательно
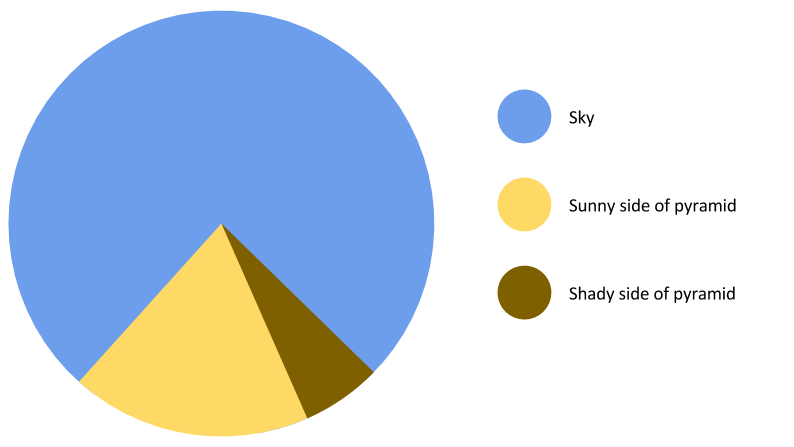
Вот клевая инфографика с лекции, которая мне понравилась
Лекция вызвала ностальгию, вспомнил, как во Владивосток приезжал Шарыгин и делал разбор олимпиадных задач. Савватеев жег не хуже.
Но вернемся к нашим треугольникам.
В ходе простейших выкладок можно прийти к формуле:
а/(в+с)+в/(а+с)=с/(а+в) — необходимое условие, которое выполняется в том случае, если маленький треугольник равнобедренный, где а, в, с, стороны нашего первоначального треугольника.
Магия в том, что такой треугольник, удовлетворяющий условиям, вписан в семигранник

Далее Алексей быстренько ввел проективную прямую, ввел сложение точек, показал, как, зная одно рациональное решение, методом итераций можно получить кучу других решений.

«Мой друг ушел из математики в бизнес. Но так как в бизнесе душа умирает, а в математике душа воскрешает, друг по вечерам воскресал свою душу. Звонит он мне однажды и говорит: «Я нашел»».
Целочисленное решение найдено — 18 800 081, 1 481 089, 19 214 131
Данный целочисленный треугольник — это решение вида 9А+D
«Своей глубочайшей звериной интуицией я чую, что треугольник вида 16A тоже является целочисленным. Кто может запрограммировать это и проверить — вперед.» Сложность в том, что длина чисел увеличивается вдвое при добавлении очередного A.

«За неделю предлагаю вам выучить и разобраться с такими понятиями, как поле, группа, гомоморфизм, кольцо...»
Просыпается один школьник — «Стопэ! Точки ведь нельзя складывать!»
Естественно, я ему сказал: «Старина, ты проснулся не в той реальности».
— Тук-тук, это Яндекс-лагерь?
— Да.
— Хотите я для вас мини-курс прочитаю по 3d-печати?
— Давайте попробуем.
— Тук-тук, это printbox3d? Хотите пропиариться перед сотрудниками Яндекса? Тогда вы можете предоставить ваш 3d-принтер на 3 недели.
— Нас это устраивает.
Это было год назад, тогда мы исследовали книгу Митника «Призрак в сети», в этот раз у нас на очереди книга «Искусство обмана».

Парочка школьников побежали качать книгу себе на планшет.
Попробуем успеть написать с учениками еще одну статью на Хабр (прошлогодняя статья)
UPD Переводим книгу Kingpin
Задача: измерить высоту вот этого сооружения

Идеи:

Остальные задания инженерной олимпиады будут чуть позже.

Основа смены — работа над проектами в команде

За обеспечением мозгов кислородом следит датчик CO2
Программисты тем временем кодят «решателей» головоломок
и поддерживают китайских производителей, помогая им придумывать названия типа «Abibas»

П.С.
Если у вас есть интересные предложения игр, заданий,социальных экспериментов, предлагайте, еще есть время и живые дети, можно бесплатно протестировать свои гипотезы. Ну, или поделитесь опытом, какие задачки вы задавали детям или какие задачки задавали вам, когда вы были в лагере.
П.П.С.


Часть вещей, которые я взял с собой на смену
Я думал, что я самый безбашенный человек в лагере, пока не приехал преподаватель Яндекса. Босиком. Он отпил глоток воды из графина и сказал: «Эээх, раньше я так водку пил». Затем он прочитал искрометную лекцию и «нарисовал» множество эллиптических кривых.
Вот как Алексей Савватеев анонсировал свою лекцию:
В журнале «Квант» номер 8 за 1983 год в статье «Вокруг биссектрисы» на странице 36 И.Ф.Шарыгин формулирует такую задачу:
«Про данный треугольник известно, что треугольник, образованный основаниями его биссектрис — равнобедренный. Можно ли утверждать, что и данный треугольник равнобедренный?»
Ответ отрицательный, но в статье далее сказано:
«К сожалению, автор не сумел построить конкретный пример треугольника (то есть точно указать величины всех его углов или длины сторон) со столь экзотическим свойством. Может быть, это удастся сделать читателям журнала?»
С тех пор построены три примера. Последний пример выводит нас на теорию эллиптических кривых и операцию сложения точек.
В лекции мы построим ЦЕЛОЧИСЛЕННЫЙ треугольник, обладающий требуемым свойством. Вопрос о бесконечности таких треугольников пока ещё остаётся открытым. Школьная задача, таким образом, приведёт нас в самое сердце одной из красивейших ветвей современной математики.
Смена в самом разгаре, кое-что интересное мы уже успели сделать, а что-то еще в планах.
В лагере есть обязательные лекции, есть приезжающие лекторы, есть воркшопы, есть самостоятельная работа над проектом. Самое интересное происходит
Начал я с самого простого: чтобы в чем-то разобраться, надо это что-то разобрать. В этот раз на растерзание просится радар-детектор (не путать с антирадаром). Вслед за мной ребята разобрали два ноутбука, типа починить. (И нашли внутри одного из них линейку и таблицу перерасчета разных величин.)
Прошлые распилы: распил лазера, распил электрошокера, распил фонарика
Радар-детектор

Разберемся, что такое Ка и Кu диапазоны, что такое эффект Допплера, что такое рупорная антенна, как работает полицейский радар и лидар, как глушится радиосигнал и что такое лазерный джаммер.
Запилить игру TAMSK
«Я никогда не думал, что стану профессиональным автором игр. Просто однажды мне в голову пришла идея абстрактной игры, что-то среднее между паззлом и кубик-рубиком. За 4 дня я ее изготовил. А через пару лет, сидя в баре, познакомился с парнем, который уверял, что он придумывает настольные игры. Я рассказал ему о своей игре, он проявил интерес, зашел ко мне в гости и внимательно ее оглядел. А на следующий день пошел и зарегистрировал ее на свое имя. Приятного тут было мало, но вместо того чтобы набить ему морду я решил придумать еще пару игр. Тот парень показал мне, что свои идеи можно как-то воплощать в жизнь. Если б не он, я бы не занимался тем, чем занимаюсь сейчас». Крис Бурм

Написал я письмецо Крису Бурму, чтобы он ответил на пару вопросов и вдохновил на подвиги юных гемдизайнеров. Посмотрим, что он ответит.
В России выпущены несколько игр, но игру с самым интересным геймплеем (на мой взгляд) предали забвению. Мне захотелось реконструировать сей шедевр и подать хоть один конструктивный пример ребятам. (А то все распил, да взломы).

GIPF (1998) – игра смещения, TAMSK (1998) – игра давления, ZÈRTZ (2000) – игра пожертвований, DVONN (2001) – игра мобильности, YINSH (2003) – игра перемен, PÜNCT (2005) – игра соединения, TZAAR (2007) — игра баланса.
Правила на английском
A territorial game with time as a special feature.
The second game of Project GIPF. For 2 players.
Components
— 1 game board
— 3 red and 3 black hour-glasses (3 min.)
— 1 neutral hour-glass (15-second timer)
— 64 ivory rings
— 2 ring holders, each to hold 32 rings
Set-up
1. Starting position: see diagram below. Place the red and black hour-glasses on the 6 corner spaces of the board, so that the hour-glasses of both players alternate: black, red, black, red, black, red. The upper parts must be empty before starting a game.
2. Take a ring holder and fill it with 32 rings.
Aim
You and your opponent start the game with 32 rings each. The player with the fewest rings left at the end of the game is the winner. (This counts for all 3 levels.)
TAMSK is not difficult to learn, but because you'll have to play under constant time pressure, we advise you to get used to the rules in three stages.
Rules to learn the strategy of moving the hour-glasses without turning them over. Use them as normal pieces, not as hour-glasses.
1. Start:
Draw lots to determine who will play with the red hour-glasses. Red begins, then take turns moving your hour-glasses.
2. A move:
Each turn you must move one of your hour-glasses. You may move it to any adjacent vacant space.
3. Dropping a ring:
After moving an hour-glass, you may play one ring: take a ring from your ringholder, put it over the hour-glass you moved and then drop it. (For the remainder of the game, the ring you dropped will serve as an indication that the space has been visited earlier on.)
Note: playing a ring is optional, but since getting rid of rings is the aim of the game, you should do it (or rather: don't forget to do it). If, for any particular reason, you decide not to play a ring and your opponent notices it, then he may play one of his rings where you didn't, and he may still make his regular move.
4. The different spaces:
The spaces (tubes) on the board have different heights. Once the rings around a space are level with the height of the tube, that space may not be visited again for the remainder of the game.
· 18 spaces around the edge of the board may only have 1 ring.
· The next tier of 12 spaces may have a maximum of 2 rings.
· The inner tier of 6 spaces may have a maximum of 3 rings.
· The central space may have 4 rings.
Note: you may never move an hour-glass to a space which already has its maximum number of rings. If you do, you lose the game at once. So, watch the rings on the board carefully.
5. Passing your turn:
When you cannot move any of your hour-glasses (because all three are blocked by your opponent's hour-glasses and/or spaces you may not move to any more), you must pass your turn. You must continue to pass until you are able to move again — or until the game ends.
6. The end:
The game ends when no more moves can be made. The player with the fewest rings left wins the game. Most of the time this means that the first player who has to pass because he cannot move his hour-glasses any more, will lose. So, the aim is to get rid of rings, but it could also be said that the aim is to be the first to block all three of the opponent's hour-glasses.
7. A tie:
If both players have an equal number of rings left, the game ends in a tie.
The second level is played as described under Level 1, but with additional rules for the hour-glasses. The 15-second hour-glass is still left out of the game. The aim of this version is to get used to the time pressure caused by the pieces (i.e. the hour-glasses) and to see how it will influence your strategy.
Note: Level 1 is a game on itself, and so is level 3. Level 2 is an intermediate level; just play it a few times as an introduction to level 3.
1. Start:
The starting position remains the same.
2. The first 3 turns:
You and your opponent are obliged to use your first 3 turns to move each of your 3 hour-glasses. When moving an hour-glass, it must be turned over. Thus, after you and your opponent have made 3 moves each, the time of all 6 hour-glasses on the board will be running.
3. A move:
You must try to keep your hour-glasses alive. Each time you move an hour-glass to a vacant adjacent space (in fact, while you are moving it), it must be turned over. In other words: each turn you must reverse the time of one of your hour-glasses. A move must be made with a fluid motion; you may not keep an hour-glass in a horizontal position. You must let go of the hour-glass as soon as it is moved, i.e. you may not prevent your opponent from starting his move by holding onto your moved hour-glass. (See point 5 below: Timing of a move.)
4. Dropping a ring:
After moving an hour-glass, your turn is over, although you may still play a ring. But you must do it immediately and without hesitation after making your move. If you don't, you lose the opportunity to play a ring that turn. As described under Level 1, your opponent may put a ring where you didn't, before making his move.
5. Timing of a move:
Immediately after you have moved one of your hour-glasses, your opponent may start his move. In other words, he does not need to wait until you have dropped your ring. But as soon as he moves an hour-glass, he may not play an extra ring if you didn't play one.
6. Losing an hour-glass:
When an hour-glass runs out of time, it is lost. A lost hour-glass remains on the board but may not be moved any more.
Note: you may lose an hour-glass on purpose!
7. 15-second rule:
Even though you don't use the 15-second hour-glass, its principle is introduced as a «gentlemen's agreement»: the players have a maximum of 15 seconds to make their move. (Since it is a «gentlemen's agreement» only, there is no penalty when a player takes a bit more time than is strictly allowed. Just play quickly.)
8. The end:
The aim remains the same: getting rid of as many rings as possible.
9. No more tie:
Unlike level 1, this level cannot end in a tie. If both players have an equal number of rings left, then time will determine the winner:
· Remove the hour-glasses that have already run out of time from the board and put them aside.
· Watch the remaining hour-glasses closely. Each hour-glass that runs out of time is to be taken from the board, and lined up in the order removed.
· The player with the last «living» hour-glass on the board wins the game.
· In the rare case that the last hour-glass of both players run out of time at exactly the same time, then the player who had the last-but-one hour-glass on the board wins.
The complete game, played under constant time pressure caused by the hour-glasses and the 15-second timer. It is played as described under Levels 1 and 2, but with additional rules for the use of the 15-second hour-glass.
1. Start:
Red begins; black may decide whether the 15 second timer is to be placed to the left or right of the board.
2. The 15-second rule:
The 15-second hour-glass is available to you during your opponent's turn, but you are not obliged to use it. You may use it (i.e. turn it over) if you want to force your opponent to make his move within 15 seconds. Of course, your opponent may use it too when it is your turn.
3. The use:
To use the 15-second timer, simply turn it over, but you may only do so when the upper part is empty. So, on occasions you may have to wait until it runs out of time before you can use it against your opponent.
Note: when you have used the 15-second timer against your opponent, it is your turn again as soon as he made his move; you do not have to wait until the 15-second timer is empty.
4. Private:
If you start your move but don't finish it in the allowed amount of time (i.e. when you don’t let go of the hour-glass you moved before the 15-second timer runs out of time), you may complete the move, including dropping a ring, but you’ll have to face a penalty. Your opponent may now drop two rings with his next turn. He starts his turn with his regular (i.e. he moves an hour-glass and puts a ring in the newly covered space), and next he may drop a second rings in any space on the board, no matter whether the space is occupied by an hour-glass (of either color) or not. Of course, it is only possible to drop a ring in a space that has not yet its maximum number of rings.
Note: this is an adjusted rule. The original rules said that you had the right to play twice when your opponent didn’t finish his turn in time, but this could cause confusion in the ending stage of the game. That is fixed with this new rule.
5. Timing:
You may start your move as soon as your opponent releases the hour-glass he moved, or, if he hasn't finished his move yet, the moment the 15-second timer runs out of time (i.e. in this case you must not wait until your opponent releases the hour-glass).
6. Passing a turn:
If you have not started to move an hour-glass when the 15-second timer runs out of time, you forfeit that turn. In other words: unlike in Level 1, you may now pass your turn, but the consequence is the same as when you have not finished your turn in time, as explained in point 4. above.
Note: when you cannot make a move, this does not count as passing a turn. So, in this case the opponent may not drop 2 rings.
7. The end:
The game ends as described under level 1 and 2.
Option
It is also possible to start a game of TAMSK with the hour-glasses of the board. If you want to make use of that possibility, then use your first 3 moves to place your hour-glasses in spaces at choice with the time running, and you may immediately start dropping rings.
Enjoy the pressure!
The second game of Project GIPF. For 2 players.
Components
— 1 game board
— 3 red and 3 black hour-glasses (3 min.)
— 1 neutral hour-glass (15-second timer)
— 64 ivory rings
— 2 ring holders, each to hold 32 rings
Set-up
1. Starting position: see diagram below. Place the red and black hour-glasses on the 6 corner spaces of the board, so that the hour-glasses of both players alternate: black, red, black, red, black, red. The upper parts must be empty before starting a game.
2. Take a ring holder and fill it with 32 rings.
Aim
You and your opponent start the game with 32 rings each. The player with the fewest rings left at the end of the game is the winner. (This counts for all 3 levels.)
The game
TAMSK is not difficult to learn, but because you'll have to play under constant time pressure, we advise you to get used to the rules in three stages.
Level 1: without time pressure
Rules to learn the strategy of moving the hour-glasses without turning them over. Use them as normal pieces, not as hour-glasses.
1. Start:
Draw lots to determine who will play with the red hour-glasses. Red begins, then take turns moving your hour-glasses.
2. A move:
Each turn you must move one of your hour-glasses. You may move it to any adjacent vacant space.
3. Dropping a ring:
After moving an hour-glass, you may play one ring: take a ring from your ringholder, put it over the hour-glass you moved and then drop it. (For the remainder of the game, the ring you dropped will serve as an indication that the space has been visited earlier on.)
Note: playing a ring is optional, but since getting rid of rings is the aim of the game, you should do it (or rather: don't forget to do it). If, for any particular reason, you decide not to play a ring and your opponent notices it, then he may play one of his rings where you didn't, and he may still make his regular move.
4. The different spaces:
The spaces (tubes) on the board have different heights. Once the rings around a space are level with the height of the tube, that space may not be visited again for the remainder of the game.
· 18 spaces around the edge of the board may only have 1 ring.
· The next tier of 12 spaces may have a maximum of 2 rings.
· The inner tier of 6 spaces may have a maximum of 3 rings.
· The central space may have 4 rings.
Note: you may never move an hour-glass to a space which already has its maximum number of rings. If you do, you lose the game at once. So, watch the rings on the board carefully.
5. Passing your turn:
When you cannot move any of your hour-glasses (because all three are blocked by your opponent's hour-glasses and/or spaces you may not move to any more), you must pass your turn. You must continue to pass until you are able to move again — or until the game ends.
6. The end:
The game ends when no more moves can be made. The player with the fewest rings left wins the game. Most of the time this means that the first player who has to pass because he cannot move his hour-glasses any more, will lose. So, the aim is to get rid of rings, but it could also be said that the aim is to be the first to block all three of the opponent's hour-glasses.
7. A tie:
If both players have an equal number of rings left, the game ends in a tie.
Level 2: with time pressure
The second level is played as described under Level 1, but with additional rules for the hour-glasses. The 15-second hour-glass is still left out of the game. The aim of this version is to get used to the time pressure caused by the pieces (i.e. the hour-glasses) and to see how it will influence your strategy.
Note: Level 1 is a game on itself, and so is level 3. Level 2 is an intermediate level; just play it a few times as an introduction to level 3.
1. Start:
The starting position remains the same.
2. The first 3 turns:
You and your opponent are obliged to use your first 3 turns to move each of your 3 hour-glasses. When moving an hour-glass, it must be turned over. Thus, after you and your opponent have made 3 moves each, the time of all 6 hour-glasses on the board will be running.
3. A move:
You must try to keep your hour-glasses alive. Each time you move an hour-glass to a vacant adjacent space (in fact, while you are moving it), it must be turned over. In other words: each turn you must reverse the time of one of your hour-glasses. A move must be made with a fluid motion; you may not keep an hour-glass in a horizontal position. You must let go of the hour-glass as soon as it is moved, i.e. you may not prevent your opponent from starting his move by holding onto your moved hour-glass. (See point 5 below: Timing of a move.)
4. Dropping a ring:
After moving an hour-glass, your turn is over, although you may still play a ring. But you must do it immediately and without hesitation after making your move. If you don't, you lose the opportunity to play a ring that turn. As described under Level 1, your opponent may put a ring where you didn't, before making his move.
5. Timing of a move:
Immediately after you have moved one of your hour-glasses, your opponent may start his move. In other words, he does not need to wait until you have dropped your ring. But as soon as he moves an hour-glass, he may not play an extra ring if you didn't play one.
6. Losing an hour-glass:
When an hour-glass runs out of time, it is lost. A lost hour-glass remains on the board but may not be moved any more.
Note: you may lose an hour-glass on purpose!
7. 15-second rule:
Even though you don't use the 15-second hour-glass, its principle is introduced as a «gentlemen's agreement»: the players have a maximum of 15 seconds to make their move. (Since it is a «gentlemen's agreement» only, there is no penalty when a player takes a bit more time than is strictly allowed. Just play quickly.)
8. The end:
The aim remains the same: getting rid of as many rings as possible.
9. No more tie:
Unlike level 1, this level cannot end in a tie. If both players have an equal number of rings left, then time will determine the winner:
· Remove the hour-glasses that have already run out of time from the board and put them aside.
· Watch the remaining hour-glasses closely. Each hour-glass that runs out of time is to be taken from the board, and lined up in the order removed.
· The player with the last «living» hour-glass on the board wins the game.
· In the rare case that the last hour-glass of both players run out of time at exactly the same time, then the player who had the last-but-one hour-glass on the board wins.
Level 3: with the 15-second timer
The complete game, played under constant time pressure caused by the hour-glasses and the 15-second timer. It is played as described under Levels 1 and 2, but with additional rules for the use of the 15-second hour-glass.
1. Start:
Red begins; black may decide whether the 15 second timer is to be placed to the left or right of the board.
2. The 15-second rule:
The 15-second hour-glass is available to you during your opponent's turn, but you are not obliged to use it. You may use it (i.e. turn it over) if you want to force your opponent to make his move within 15 seconds. Of course, your opponent may use it too when it is your turn.
3. The use:
To use the 15-second timer, simply turn it over, but you may only do so when the upper part is empty. So, on occasions you may have to wait until it runs out of time before you can use it against your opponent.
Note: when you have used the 15-second timer against your opponent, it is your turn again as soon as he made his move; you do not have to wait until the 15-second timer is empty.
4. Private:
If you start your move but don't finish it in the allowed amount of time (i.e. when you don’t let go of the hour-glass you moved before the 15-second timer runs out of time), you may complete the move, including dropping a ring, but you’ll have to face a penalty. Your opponent may now drop two rings with his next turn. He starts his turn with his regular (i.e. he moves an hour-glass and puts a ring in the newly covered space), and next he may drop a second rings in any space on the board, no matter whether the space is occupied by an hour-glass (of either color) or not. Of course, it is only possible to drop a ring in a space that has not yet its maximum number of rings.
Note: this is an adjusted rule. The original rules said that you had the right to play twice when your opponent didn’t finish his turn in time, but this could cause confusion in the ending stage of the game. That is fixed with this new rule.
5. Timing:
You may start your move as soon as your opponent releases the hour-glass he moved, or, if he hasn't finished his move yet, the moment the 15-second timer runs out of time (i.e. in this case you must not wait until your opponent releases the hour-glass).
6. Passing a turn:
If you have not started to move an hour-glass when the 15-second timer runs out of time, you forfeit that turn. In other words: unlike in Level 1, you may now pass your turn, but the consequence is the same as when you have not finished your turn in time, as explained in point 4. above.
Note: when you cannot make a move, this does not count as passing a turn. So, in this case the opponent may not drop 2 rings.
7. The end:
The game ends as described under level 1 and 2.
Option
It is also possible to start a game of TAMSK with the hour-glasses of the board. If you want to make use of that possibility, then use your first 3 moves to place your hour-glasses in spaces at choice with the time running, and you may immediately start dropping rings.
Enjoy the pressure!
Первый прототип

Работа продолжается, а вожатые и дети выстроились в очередь, чтоб поиграть в нее. Надеюсь, до конца смены успею. Жаль, что есть баг: в часах разное количество песка, погрешность по времени до 20%.
Сенсорное замещение и нейропластичность

В 2004 году немецкие ученые из университета в Оснабрюке во главе с Питером Кёнигом успешно провели эксперимент по внедрению человеку нового чувства. Участники эксперимента полтора месяца носили массивный пояс с электронным компасом, датчики которого вибрировали, будучи направленными на север. Они, подобно птицам, научились чувствовать магнитное поле земли и вот как пытались описать свои ощущения: «Я интуитивно ощущал направление к моему дому или офису. Я мог стоять в очереди в кафе и вдруг подумать: я живу вон там». Или: «В течение первых двух недель мне надо было концентрироваться. Затем все происходило интуитивно. Я мог даже представить расположение мест и помещений, где я когда-то был».

Исходный код для проекта

Пояс немецких коллег

Вот из этого мы будем паять свой пояс всевластия
Видео про встраивание в мозг новых чувств
http://www.youtube.com/watch?v=lmYyhuN0S2c
Наручники
Есть много мифов о том, как наручники взламывают фантиками и зубочистками, ломают цепь руками.
Попробуем развенчать мифы про взлом наручников и рассмотрим все фичи и баги нормальных наручников, которые есть в любом интернет-магазине.
Хакеры взламывают наручники на DefCon
Сижу, ковыряюсь шпилькой в наручниках и тут в домик постучался вежливый мужчина в галстуке и представился службой безопасности коттеджного поселка. Я немного побледнел. Но оказалось, его интересовал вопрос, не выкорчует ли мой слэклайн его любимую елочку.

Лекция от Рамблера
Препод рассказал про игрули, Симпсонов и Гриффинов с точки зрения дизайна

Слушали очень внимательно
Вот клевая инфографика с лекции, которая мне понравилась
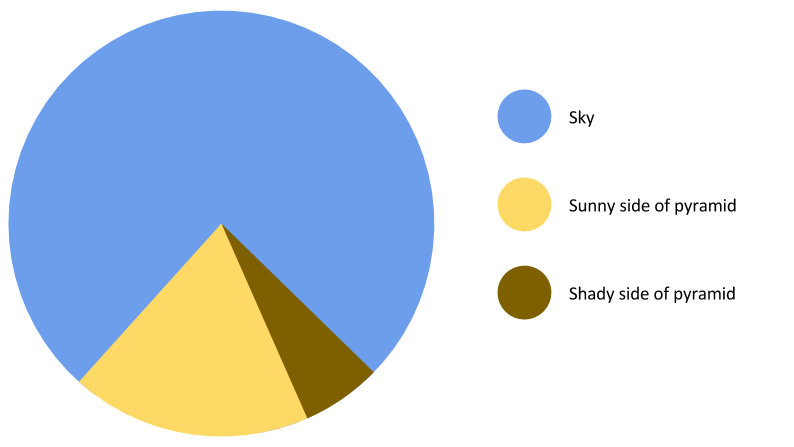
Лекция от Яндекса

Лекция вызвала ностальгию, вспомнил, как во Владивосток приезжал Шарыгин и делал разбор олимпиадных задач. Савватеев жег не хуже.
Но вернемся к нашим треугольникам.
В ходе простейших выкладок можно прийти к формуле:
а/(в+с)+в/(а+с)=с/(а+в) — необходимое условие, которое выполняется в том случае, если маленький треугольник равнобедренный, где а, в, с, стороны нашего первоначального треугольника.
Магия в том, что такой треугольник, удовлетворяющий условиям, вписан в семигранник

Далее Алексей быстренько ввел проективную прямую, ввел сложение точек, показал, как, зная одно рациональное решение, методом итераций можно получить кучу других решений.

«Мой друг ушел из математики в бизнес. Но так как в бизнесе душа умирает, а в математике душа воскрешает, друг по вечерам воскресал свою душу. Звонит он мне однажды и говорит: «Я нашел»».
Целочисленное решение найдено — 18 800 081, 1 481 089, 19 214 131
Данный целочисленный треугольник — это решение вида 9А+D
«Своей глубочайшей звериной интуицией я чую, что треугольник вида 16A тоже является целочисленным. Кто может запрограммировать это и проверить — вперед.» Сложность в том, что длина чисел увеличивается вдвое при добавлении очередного A.

«За неделю предлагаю вам выучить и разобраться с такими понятиями, как поле, группа, гомоморфизм, кольцо...»
Просыпается один школьник — «Стопэ! Точки ведь нельзя складывать!»
Естественно, я ему сказал: «Старина, ты проснулся не в той реальности».
Видео с другими лекциями Алексея Савватеева
Социальная инженерия
— Тук-тук, это Яндекс-лагерь?
— Да.
— Хотите я для вас мини-курс прочитаю по 3d-печати?
— Давайте попробуем.
— Тук-тук, это printbox3d? Хотите пропиариться перед сотрудниками Яндекса? Тогда вы можете предоставить ваш 3d-принтер на 3 недели.
— Нас это устраивает.
Это было год назад, тогда мы исследовали книгу Митника «Призрак в сети», в этот раз у нас на очереди книга «Искусство обмана».

Мой переход от телефонного фрикинга к хакингу произошёл в старших классах, когда я столкнулся с так называемой социальной инженерией и встретил другого студента, также увлечённого фрикингом. Телефонный фрикинг – это разновидность хакинга, когда вы исследуете телефонные сети, эксплуатируя телефонные системы и служащих телефонных компаний. Он показал мне некоторые уловки, которые он мог делать с телефонами, вроде получения любой информации телефонной компании о её клиентах и использования секретных тестовых номеров, чтобы делать бесплатные звонки на дальние расстояния. Бесплатные только для нас – намного позднее я узнал, что это были вовсе не секретные номера: счета приходили какому-нибудь абоненту MCI. Это было моё знакомство с социальной инженерией – мой детский сад, так сказать. Он и другой телефонный фрикер, которого я встретил позднее, давали мне послушать свои звонки в телефонную компанию. Я узнал, как заставить себя звучать убедительно и узнал о различных офисах и процедурах телефонной компании. Но это «обучение» продолжалось недолго. Вскоре я всё это делал сам, даже лучше, чем мои первые учителя. Направление моей жизни на ближайшие 15 лет было определено.
Одной из моих любимейших шуток был захват неавторизованного доступа к телефонному коммутатору и подмена класса телефонной службы моего товарища по фрикингу. Когда он хотел позвонить из дома, то получал сообщение опустить гривенник, потому что коммутатор телефонной компании воспринимал его телефон как общественный телефон-автомат.
Я изучал всё, что касается телефонов: не только электронику, коммутаторы и компьютеры, но также организацию корпорации, процедуры и терминологию. Вскоре я, возможно, знал о телефонной системе больше, чем любой из служащих.
И я развил мои навыки в социальной инженерии настолько, что к 17 годам я мог говорить с большинством из работников Telco почти о чём угодно, лично или по телефону. Моя хакерская карьера началась в старшей школе. Тогда мы использовали термин хакер к человеку, который потратил огромное количество времени, копаясь с софтом и железом, разрабатывал более эффективные программы или исключал всё ненужное, чтобы сделать работу быстрее.
В конце 1979 (Кевину 16 лет) группа хакеров из Los Angeles Unified School District предложила мне взломать The Ark, компьютерную систему Digital Equipment Corporation, использовавшуюся для разработки софта для их операционной системы RSTS/E. Я хотел быть принятым в эту хакерскую группу, чтобы я мог узнать у них больше об операционных системах. Эти новые «друзья» знали номер диал-апа компьютерной системы DEC. Но они не могли войти без имени аккаунта и пароля. Когда вы кого-то недооцениваете, он может вернуться и ударить с фланга. В данном случае это был я, сумевший взломать систему DEC в столь юном возрасте. Представившись Антоном Черновым (Anton Chernoff), одним из ведущих разработчиков проекта, я просто позвонил системному администратору. Я заявил, что не могу войти в один из «моих» аккаунтов, и убедил этого парня достаточно, чтобы он предоставил мне доступ и позволил мне выбрать пароль по своему усмотрению. В защите экстра класса любой пользователь, соединяющийся с системой, должен был ввести диал-ап пароль. Системный администратор дал мне его. Это был пароль «buffoon» (клоун), которым, я думаю, он себя почувствовал, когда стало понятно, что произошло. Менее чем за 10 минут я получил доступ к RSTE/E системе DEC. И я вошёл не как обычный пользователь, у меня были все привилегии системного разработчика. Поначалу мои новые так называемые друзья не поверили, что я получил доступ к The Ark. Один из них отпихнул меня от клавиатуры с лицом, выражающим недоверие. Его рот открылся, когда он увидел, что я в привилегированном аккаунте. Позднее я обнаружил, что они начали копирование исходного кода компонентов к операционной системе DEC. Теперь была моя очередь удивляться. Когда они скопировали софт, они позвонили в отдел безопасности корпорации DEC и сказали, что кое-кто взломал корпоративную сеть компании. И выдали моё имя. Мои так называемые друзья сначала использовали мой доступ к исходному коду высокой секретности, а затем меня подставили.
Это был урок, и ещё не один такой урок мне пришлось выучить. Через несколько лет я неоднократно сталкивался с неприятностями, потому что я доверял людям, которых считал своими друзьями. После школы я изучал компьютеры в Обучающем Компьютерном Центре в Лос-Анджелесе.
Через несколько месяцев мой школьный компьютерный администратор догадался, что я обнаружил уязвимость в их операционной системе и получил полные привилегии администратора на их миникомпьютере IBM. Лучшие компьютерные эксперты из их преподавательского штата не смогли найти, как я это сделал. Это был один из моих ранних опытов «найма на работу». Мне сделали предложение, от которого я не смог отказаться: сделать почётный проект по повышению безопасности школьного компьютера или предстать перед обвинением во взломе системы. Конечно, я выбрал почётный проект и с Почестью окончил Cum Laude.
Парочка школьников побежали качать книгу себе на планшет.
Попробуем успеть написать с учениками еще одну статью на Хабр (прошлогодняя статья)
UPD Переводим книгу Kingpin
Инженерная олимпиада
Задача: измерить высоту вот этого сооружения

Идеи:
- померить скорость звука (не сделали)
- кинуть тапок и измерить время падения (не сделали)
- сфотали с человеком рядом и померили по фотографии в попугаях
- прикинули, что высота равна радиусу, а радиус измерили
- а) в шагах
б) ростом
в) дощечками

Остальные задания инженерной олимпиады будут чуть позже.
Проекты

Основа смены — работа над проектами в команде
Подробнее
Поначалу вот так и выглядели все проекты
Некоторые не выдержали испытаний

Остатки робота-амфибии встретились с остатками робота-барабанщика
Некоторые успешно функционируют

Робот-сканер для картирования помещений

Робот-ездок по палке, в помощь кинооператорам

Поначалу вот так и выглядели все проекты
Некоторые не выдержали испытаний

Остатки робота-амфибии встретились с остатками робота-барабанщика
Некоторые успешно функционируют

Робот-сканер для картирования помещений
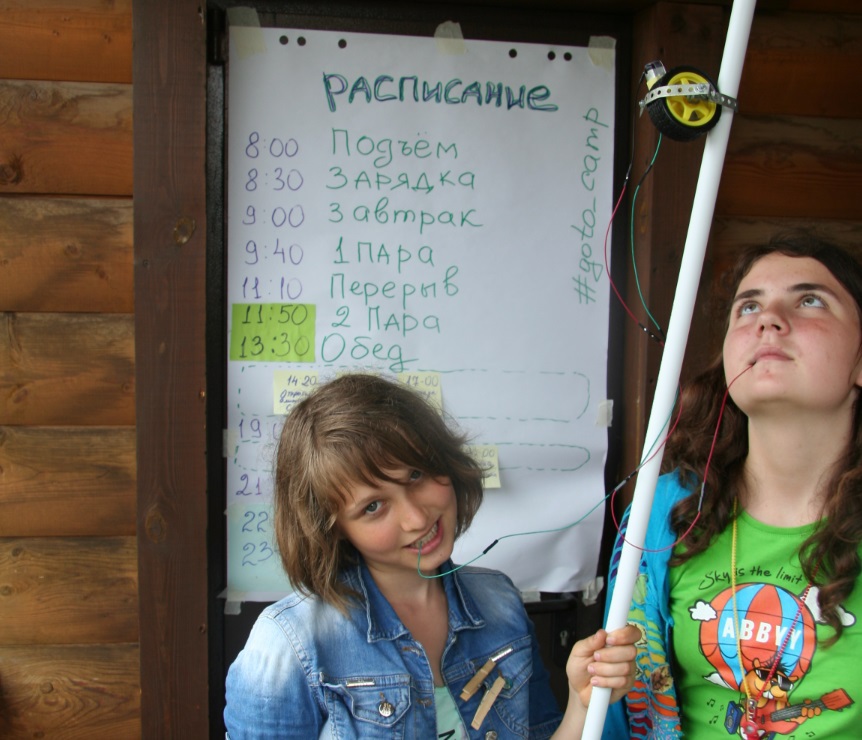
Робот-ездок по палке, в помощь кинооператорам

За обеспечением мозгов кислородом следит датчик CO2
Программисты тем временем кодят «решателей» головоломок
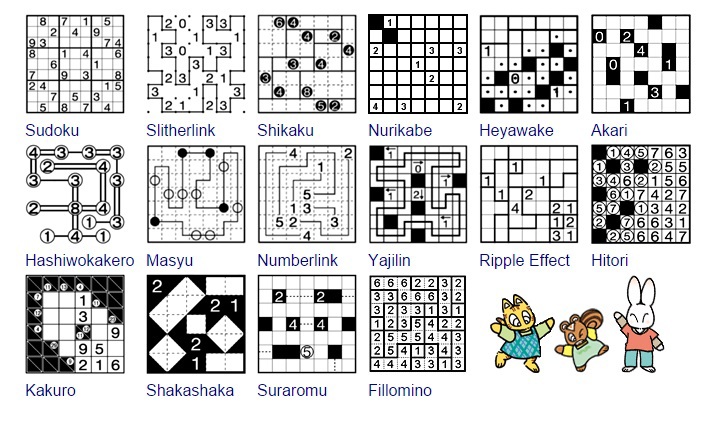
и поддерживают китайских производителей, помогая им придумывать названия типа «Abibas»
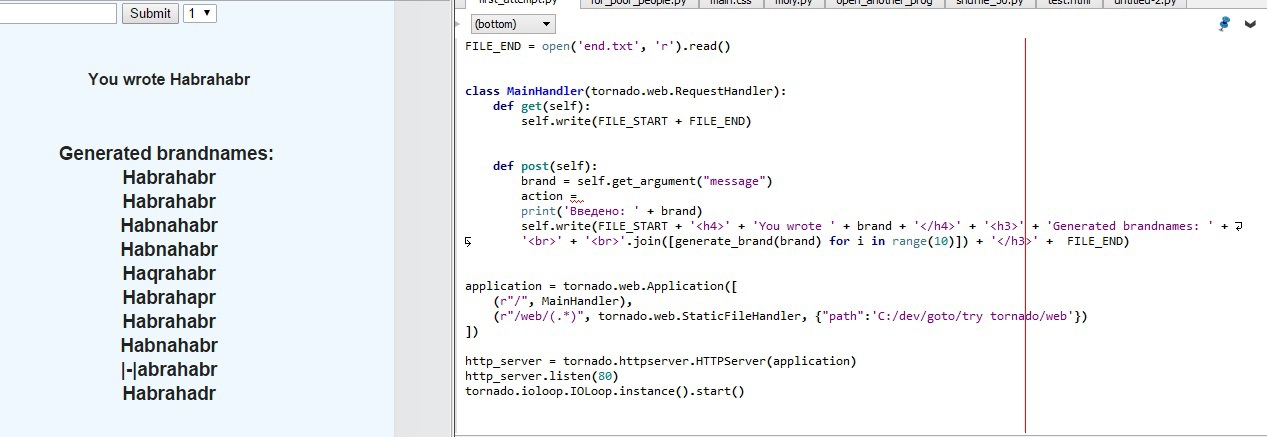
П.С.
Если у вас есть интересные предложения игр, заданий,
П.П.С.
