Генератор случайных чисел во многом подобен сексу: когда он хорош — это прекрасно, когда он плох, все равно приятно (Джордж Марсалья, 1984)
Популярность стохастических алгоритмов все растет. Многие из них базируются на генерации большого количества различных случайных величин. Далеко не всегда равномерно распределенных. Здесь я попытался собрать информацию о быстрых и точных генераторах случайных величин с известными распределениями. Задачи могут быть разными, разными могут быть и критерии. Кому-то важно время генерации, кому-то — точность, кому-то — криптоустойчивость, кому-то — скорость сходимости. Лично я исходил из предположения, что мы имеем некий базовый генератор, возвращающий псевдослучайное целое число, равномерно распределенное от 0 до некого RAND_MAX
unsigned long long BasicRandGenerator() {
unsigned long long randomVariable;
// some magic here
...
return randomVariable;
}
и что этот генератор достаточно быстрый. Я имею ввиду, что дешевле сгенерировать с десяток случайных чисел, нежели чем посчитать логарифм или возвести в степень одно из них. Это могут быть стандартные генераторы: std::rand(), rand в MATLAB, Java.util.Random и т.д. Но имейте ввиду, что подобные генераторы редко подходят для серьезной работы. Зачастую они проваливают разные статистические тесты. А также, помните, что вы полностью зависите от них и лучше использовать свой собственный генератор, чтобы иметь представление о его работе.
В статье я буду рассказывать об алгоритмах, суть которых должна быть понятна каждому, кто хоть иногда сталкивался с теорией вероятностей. Совсем необязательно быть знакомым с теорией меры, как правило, достаточно примерно понимать, что из себя представляют функция распределения и функция плотности распределения:
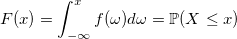
Каждый алгоритм я буду сопровождать кодом, небольшим количеством математики и гистограммой из десятка миллионов сгенерированных случайных величин.
Равномерное распределение
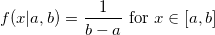
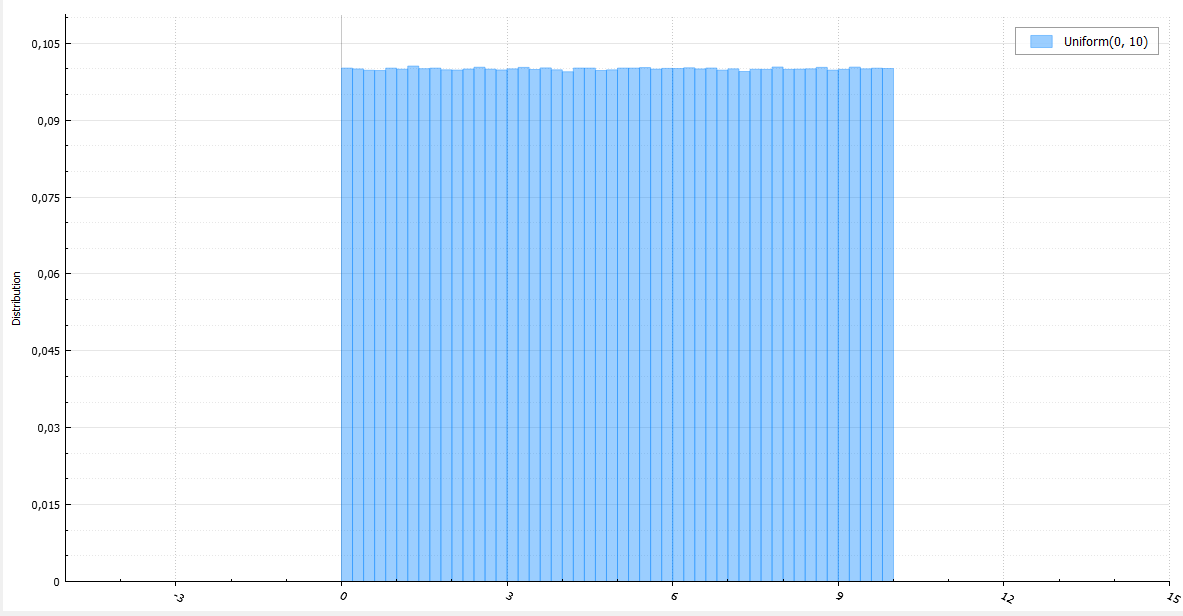
Равномерное распределение может использоваться при генерации почти что любой случайной величины, благо имеется очень простой и универсальный метод инверсии (inverse transform sampling): генерируем случайную величину U, равномерно распределенную от 0 до 1, и возвращаем обратную функцию распределения (квантиль) с параметром U. Действительно:
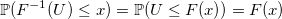
Проблема в том, что подсчет обратной функции распределения может быть долгим, если вообще аналитически возможен.
С генератором равномерного распределения, я надеюсь, мне не нужно долго останавливаться (при большом количестве генерируемых случайных величин лучше посчитать (b — a) / RAND_MAX только один раз):
double Uniform(double a, double b) {
return a + BasicRandGenerator() * (b - a) / RAND_MAX;
}
Разумеется, непрерывность — это лишь абстракция. В реальном мире и в данном случае конкретно под этим подразумевается достаточно малый шаг дискретизации. Стоит заметить важную вещь. Если вы генерируете случайное число, равномерно распределенное от 0 до 1, то 32 бит недостаточно, чтобы покрыть все значения, которые может принимать на этом диапазоне double (хотя, для float этого более чем достаточно). Для лучшего качества нужно либо генерировать 64-битные целые, либо комбинировать два 32-битных.
Нормальное распределение
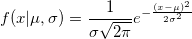
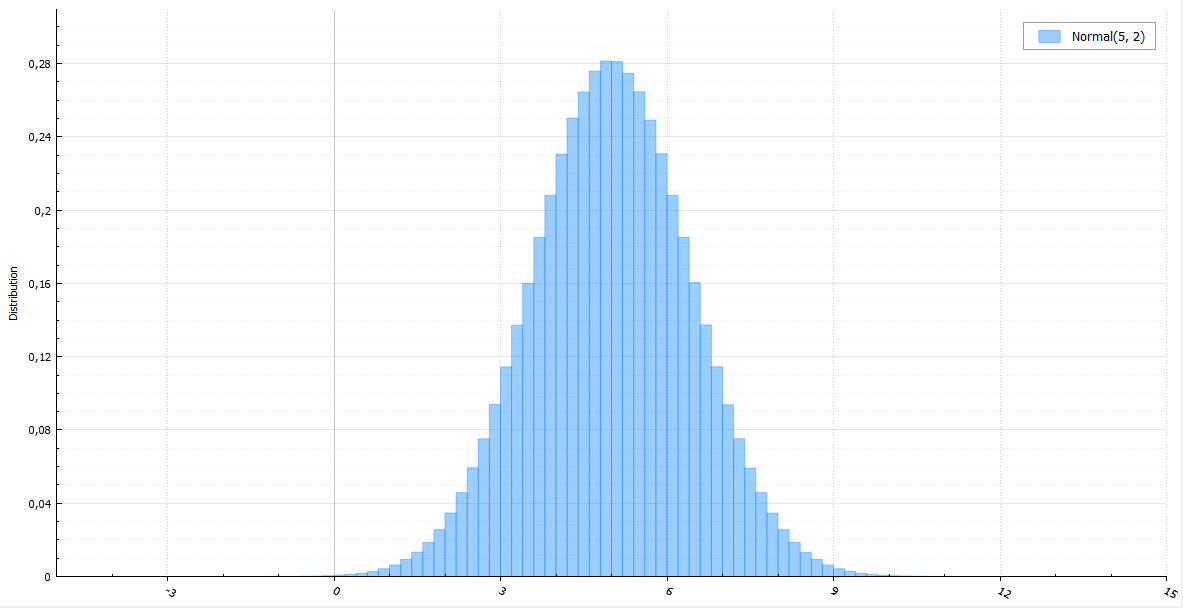
Метод инверсии потребует вычисления обратной функции ошибок. Если не использовать специальные аппроксимирующие функции, сложно и невероятно долго. Для нормальной величины существует метод Бокса-Мюллера. Он довольно прост и широко распространен. Его явный недостаток — это вычисление трансцендентных функций. На Хабре уже упоминался полярный метод, помогающий избежать подсчета синуса и косинуса. Но мы все еще должны считать логарифм и корень из него. Куда быстрее работает красиво названный метод Ziggurat, придуманный Джорджем Марсалья, автором того же полярного метода.
Полярный метод — это пример выборки с отклонением (acceptance-rejection sampling). Буквально, вы генерируете величину и принимаете ее, если она подходит, иначе — отклоняете и генерируете еще раз. Основной пример: нужно сгенерировать случайную величину с плотностью f(x), однако это слишком сложно сделать простым методом инверсии. Зато, вы можете сгенерировать случайную величину с плотностью g(x), не очень сильно отличающейся от f(x). В таком случае вы берете наименьшую константу M, такую что M > 1 и почти всюду f(x) < Mg(x), и выполняете следующий алгоритм:
- Генерируем случайную величину X из распределения g(x) и случайную величину U, равномерно распределенную от 0 до 1.
- Если U < f(X) / Mg(X) — возвращаем X, иначе — повторяем заново.
Вероятность принять случайную величину:
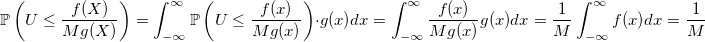
Чем меньше вы выберете M — тем больше эта вероятность — тем быстрее будет работать генератор.
Доказательство работы алгоритма:
Воспользовавшись тем, что вероятность происхождения двух событий А и B равна

вычислим вероятность принятия случайной величины X с функцией плотности распределения g(x) и функцией распределения G(x), но уже при условии, что она меньше некого заданного параметра x:

И тогда по теореме Байеса:
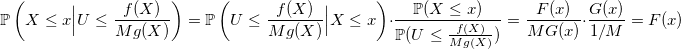

вычислим вероятность принятия случайной величины X с функцией плотности распределения g(x) и функцией распределения G(x), но уже при условии, что она меньше некого заданного параметра x:

И тогда по теореме Байеса:

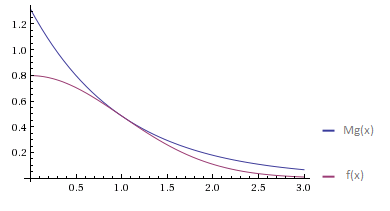
Для примера сгенерируем модуль стандартной нормальной величины. В силу симметрии нормального распределения полученную величину можно умножить на случайную величину, принимающую значения +1 и -1 с равными вероятностями, и таким образом получить стандартную нормально распределенную величину X. Любая нормальная величина получается из стандартной умножением на sigma и сдвигом на mu. Функция плотности распределения |X|:

Попытаемся её приблизить функцией плотности стандартного экспоненциального распределения. Я немного забегаю вперед, так как об экспоненциальном распределении еще не говорил. Оно генерируется просто пресловутым методом инверсии — берем равномерно распределенную на [0, 1] величину U и возвращаем -ln(U).

Минимальное значение М, удовлетворяющее условию f(x) < Mg(x), достигается при x = 1:

Тогда:
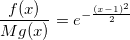
И алгоритм для генерации нормальной случайной величины будет следующим:
- Генерируем U — равномерно распределенную на [0, 1] случайную величину.
- Генерируем экспоненциально распределенную случайную величину E (об алгоритме, более быстром, чем подсчет -ln(U), расскажу далее).
- Если U < exp(-(E — 1)2) — то |X| = E, иначе возвращаемся на первый шаг.
- Генерируем новую U. Если U < 0.5, то возвращаем -|X|, или же |X| в другом случае.
Несложно заметить, что:

А это значит, что вместо U можно сгенерировать еще одну экспоненциально распределенную величину и не считать показательную функцию. Новый алгоритм будет выглядеть следующим образом:
- Генерируем стандартные экспоненциально распределенные случайный величины E1 и E2.
- Если E2 > (E1 — 1)2 / 2, то принимаем |X| = E1, иначе возвращаемся назад.
- Генерируем U. Если U < 0.5, то возвращаем -|X|, или же |X| в другом случае.
Еще один момент: при условии принятия величины E1 разница E2 — (E1 — 1)2 / 2 будет также распределена экспоненциально и независимо от E1. Поэтому её можно запомнить и использовать в следующий раз вместо E1.
Доказательство
Экспоненциальное распределение обладает свойством отсутствия памяти:

А это означает, что функция распределения разницы:
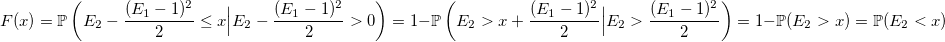

А это означает, что функция распределения разницы:

Общая проблема выборки с отклонением заключается в подборе такой случайной величины с плотностью распределения g(x), чтобы отклонений было как можно меньше. Для решения этой проблемы существует множество расширений. Сам же метод является основой для почти все последующих алгоритмов, включая Ziggurat. Суть последнего все та же: пытаемся покрыть функцию плотности нормального распределения похожей и более простой функцией и возвращаем величины, попавшие под кривую. Функция своеобразная и напоминает многоступенчатое сооружение, откуда, собственно, и такое название у алгоритма.
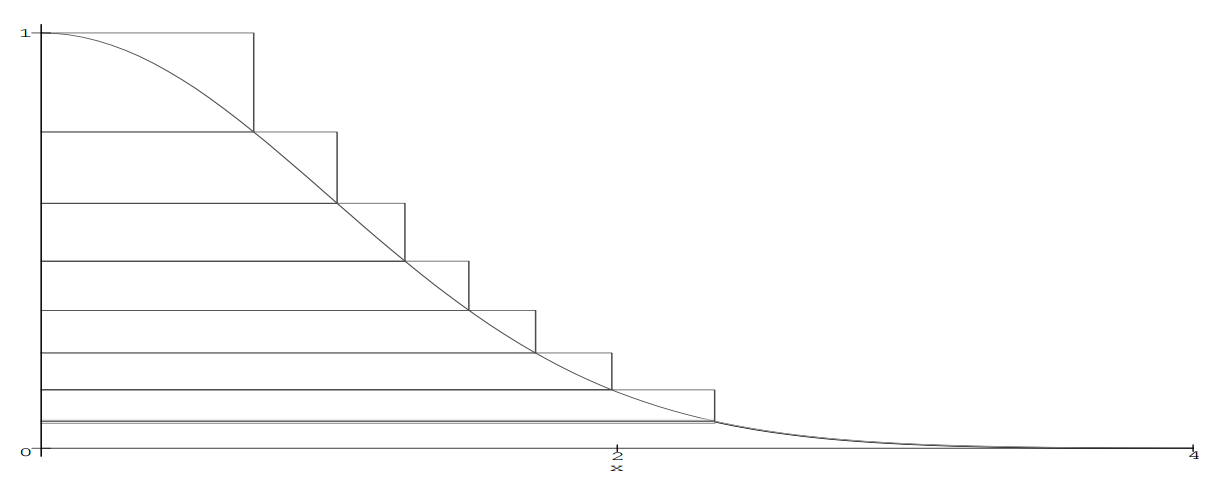
Зиккурат сооружается следующим образом. У подножья функции f(x) выбираются точки x1 и y0 = f(x1). Площадь под прямоугольником от (0,0) до (x1, y0) + площадь под хвостом функции f(x > x1) = А. Так мы построили базовый слой. Поверх него ставится еще один прямоугольник, такой, что его ширина x1, а высота y1 = A/y0 и таким образом его площадь будет равна A. Этот прямоугольник уже включает в себя точки, которые лежат выше функции f(x), например (x1, y1). Функцию f(x) второй прямоугольник пересекает в точке (x2, y1) — это будет координата нижней правой точки третьего прямоугольника, который накладывается таким же образом как и второй, чтобы его площадь была равна А. Так продолжается до тех пор, пока мы не построим Зиккурат до вершины функции. Площадь каждой ступени будет равна А. Дальнейший алгоритм (без обработки попадания в базовый слой):
- Случайно и равномерно выбирается прямоугольник i и генерируется равномерно распределенная величина X от 0 до xi
- Если X < xi+1, то мы точно попали под кривую — возвращаем X.
- Генерируем новую равномерно распределенную величину Y от yi до yi+1. Если точка с координатами (X, Y) лежит под кривой, то есть Y < f(X) — возвращаем X. Иначе возвращаемся на первый шаг.
Что делать если попали в базовый слой? Из него также можно сделать прямоугольник с площадью А, введя мнимую точку x0 = A/y0. Тогда площадь прямоугольника от (0,0) до (x0, y0) будет также равняться А. Разница в базовом слое в том, что если мы не попали под кривую в новом мнимом прямоугольнике, то мы еще не должны отклонять x — мы лишь попали в хвост. Для хвоста Джордж Марсалья предлагает воспользоваться тем же методом, что мы рассматривали до этого — выборкой с отклонением. Только с некоторыми изменениями:
- Генерируем стандартные экспоненциально распределенные случайный величины E1 с плотностью x1 и E2 с единичной плотностью.
- Если E2 > E12 / 2, то принимаем |X| = E1 + x1, иначе возвращаемся назад.
- Генерируем U. Если U < 0.5, то возвращаем -|X|, или же |X| в другом случае.
Доказательство для хвоста
Мы знаем, что случайная величина |X| > x1. Постараемся построить для нее алгоритм выборки с отклонением, используя E1+x1, где E1 — экспоненциально распределенная случайная величина с плотностью x1. Функция плотности распределения E1+x1:

Чтобы знать значение М, нам нужно найти максимум отношения функций:
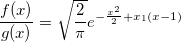
Точка x, соответствующая максимуму дроби, будет доставлять максимум степени экспоненты. Приравняв производную степени к нулю, находим, соответствующий x:
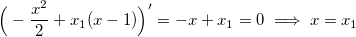
Получаем границу для равномерной случайной величины:

И тогда условие принятия случайной величины будет:
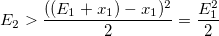

Чтобы знать значение М, нам нужно найти максимум отношения функций:

Точка x, соответствующая максимуму дроби, будет доставлять максимум степени экспоненты. Приравняв производную степени к нулю, находим, соответствующий x:

Получаем границу для равномерной случайной величины:

И тогда условие принятия случайной величины будет:
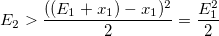
Тогда полностью алгоритм будет выглядеть так:
- Случайно и равномерно выбирается прямоугольник i и генерируется равномерно распределенная величина X от 0 до xi.
- Если X < xi + 1, то мы точно попали под кривую — возвращаем X.
- Если попали в базовый слой, то есть i = 0, то запускаем алгоритм для хвоста и возвращаем его результат.
- Генерируем новую равномерно распределенную величину Y от yI до yi + 1. Если точка с координатами (X, Y) лежит под кривой, то есть Y < f(X) — возвращаем X. Иначе возвращаемся на первый шаг.
Вопрос в том, как найти константы А и x1 в зависимости от числа прямоугольников? Можно их найти обыкновенным численным методом. Берем начальное предположение x1, строим базовый слой, вычисляем А и строим зиккурат пока не построили нужное количество прямоугольников. Если мы оказались выше функции — значит мы взяли слишком маленькое значение x1 и слишком большое значение А — пытаемся построить с новыми значениями заново.
Сам алгоритм можно ускорить различными хитростями работы с 32-битными целыми, убирая ненужные перемножения. Для большей информации можно обратиться к статье George Marsaglia and Wai Wan Tsang «The Ziggurat Method for Generating Random Variables». Здесь я представляю не до конца оптимизированный, но зато понятный код (с учетом, что мы умеем генерировать экспоненциальное распределение).
static double stairWidth[257], stairHeight[256];
const double x1 = 3.6541528853610088;
const double A = 4.92867323399e-3; /// area under rectangle
void setupNormalTables() {
// coordinates of the implicit rectangle in base layer
stairHeight[0] = exp(-.5 * x1 * x1);
stairWidth[0] = A / stairHeight[0];
// implicit value for the top layer
stairWidth[256] = 0;
for (unsigned i = 1; i <= 255; ++i)
{
// such x_i that f(x_i) = y_{i-1}
stairWidth[i] = sqrt(-2 * log(stairHeight[i - 1]));
stairHeight[i] = stairHeight[i - 1] + A / stairWidth[i];
}
}
double NormalZiggurat() {
int iter = 0;
do {
unsigned long long B = BasicRandGenerator();
int stairId = B & 255;
double x = Uniform(0, stairWidth[stairId]); // get horizontal coordinate
if (x < stairWidth[stairId + 1])
return ((signed)B > 0) ? x : -x;
if (stairId == 0) // handle the base layer
{
static double z = -1;
double y;
if (z > 0) // we don't have to generate another exponential variable as we already have one
{
x = Exponential(x1);
z -= 0.5 * x * x;
}
if (z <= 0) // if previous generation wasn't successful
{
do {
x = Exponential(x1);
y = Exponential(1);
z = y - 0.5 * x * x; // we storage this value as after acceptance it becomes exponentially distributed
} while (z <= 0);
}
x += x1;
return ((signed)B > 0) ? x : -x;
}
// handle the wedges of other stairs
if (Uniform(stairHeight[stairId - 1], stairHeight[stairId]) < exp(-.5 * x * x))
return ((signed)B > 0) ? x : -x;
} while (++iter <= 1e9); /// one billion should be enough
return NAN; /// fail due to some error
}
double Normal(double mu, double sigma) {
return mu + NormalZiggurat() * sigma;
}
Экспоненциальное распределение
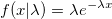
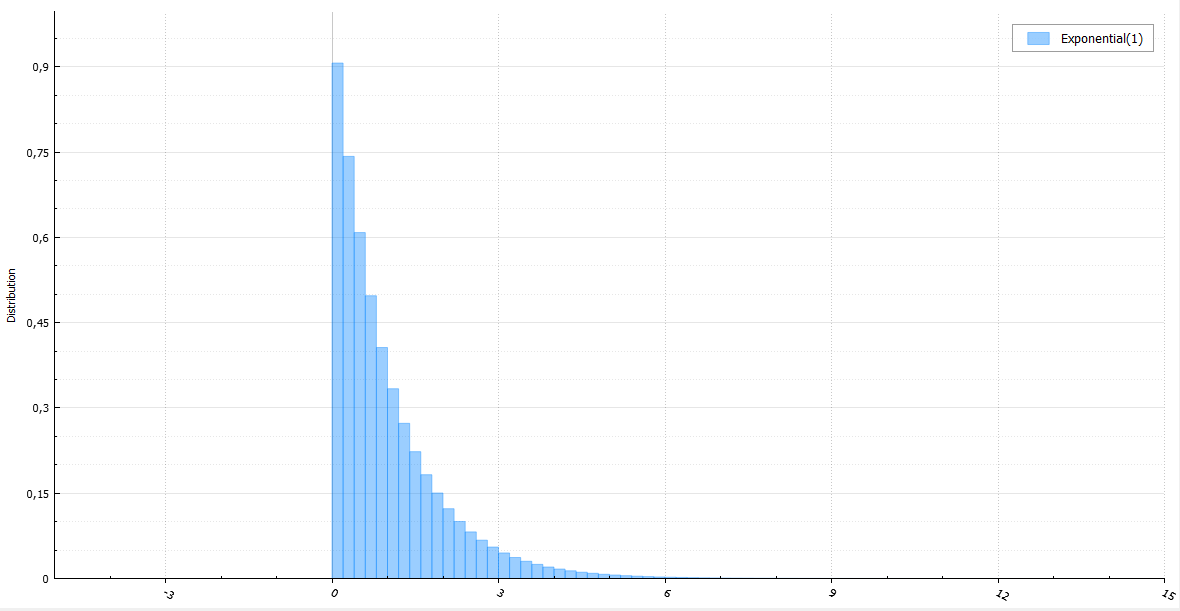
Уже говорилось, что для экспоненциального распределения можно взять логарифм от равномерно распределенной величины и что можно сделать генерацию быстрее. Так как любая экспоненциальная величина получается из стандартной делением на плотность, генерацию можно сделать пресловутым Ziggurat. В случае попадания в хвост можно запустить алгоритм по новой и прибавить к полученной величине x1:
Доказательство
Нужно доказать, что при Е > x1 функция распределения E — x1 будет также распределена экспоненциально. Это возможно благодаря ранее упомянутому отсутствию памяти у экспоненциального распределения:
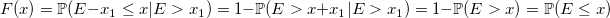

Еще пара фактов: если использовать таблицу с 255 прямоугольниками, то вероятность принятия с первого раза для экспоненциального распределения — 0.989, для нормального — 0.993. В MATLAB с 5 версии для нормального распределения используется Ziggurat (раньше использовался полярный метод). В R для нормальных величин, насколько мне известно, аппроксимируют полиномами обратную функцию ошибок и используют метод инверсии.
static double stairWidth[257], stairHeight[256];
const double x1 = 7.69711747013104972;
const double A = 3.9496598225815571993e-3; /// area under rectangle
void setupExpTables() {
// coordinates of the implicit rectangle in base layer
stairHeight[0] = exp(-x1);
stairWidth[0] = A / stairHeight[0];
// implicit value for the top layer
stairWidth[256] = 0;
for (unsigned i = 1; i <= 255; ++i)
{
// such x_i that f(x_i) = y_{i-1}
stairWidth[i] = -log(stairHeight[i - 1]);
stairHeight[i] = stairHeight[i - 1] + A / stairWidth[i];
}
}
double ExpZiggurat() {
int iter = 0;
do {
int stairId = BasicRandGenerator() & 255;
double x = Uniform(0, stairWidth[stairId]); // get horizontal coordinate
if (x < stairWidth[stairId + 1]) /// if we are under the upper stair - accept
return x;
if (stairId == 0) // if we catch the tail
return x1 + ExpZiggurat();
if (Uniform(stairHeight[stairId - 1], stairHeight[stairId]) < exp(-x)) // if we are under the curve - accept
return x;
// rejection - go back
} while (++iter <= 1e9); // one billion should be enough to be sure there is a bug
return NAN; // fail due to some error
}
double Exponential(double rate) {
return ExpZiggurat() / rate;
}
Гамма-распределение


Алгоритмы для генерации здесь уже сложнее, поэтому я не буду здесь описывать их доказательства, привожу лишь примеры. Для генерации стандартной величины (theta = 1), используются четыре алгоритма, каждый в зависимости от k.
- Если k или 2k — целое и k < 5 — GA алгоритм.
- Если k < 1 — GS алгоритм.
- Если 1 < k < 3 — GF алгоритм.
- Если k > 3 — GO алгоритм.
Нестандартная случайная величина с гамма-распределением, получается из стандартной умножением на theta.
Алгоритм GA
Если сложить две случайные величины с гамма-распределением с параметрами k1 и k2, то получится случайная величина с гамма-распределением и с параметром k1+k2. Еще одно свойство — если theta = k = 1, то легко проверить, что распределение будет экспоненциальным. Поэтому, если k целое — то можно просто просуммировать k случайных величин со стандартным экспоненциальным распределением.
double GA1(int k) {
double x = 0;
for (int i = 0; i < k; ++i)
x += Exponential(1);
return x;
}
Если k не целое, но 2k — целое, то можно вместо одной из экспоненциальных случайных величин в сумме использовать половину квадрата нормальной величины. Почему так возможно, станет ясно позднее.
double GA2(double k) {
double x = Normal(0, 1);
x *= 0.5 * x;
for (int i = 1; i < k; ++i)
x += Exponential(1);
return x;
}
Алгоритм GS
- Генерируем стандартную экспоненциально распределенную величину Е и величину U, равномерно распределенную от 0 до 1 + k / e. Если U <= 1, то переходим к шагу 2. Иначе, к шагу 3.
- Задаем x = U1/k. Если x <= E, то возвращаем x, иначе возвращаемся назад на шаг 1.
- Задаем x = -ln((1 — U) / k + 1 / e). Если (1 — k) * ln(x) <= E, то возвращаем x, иначе возвращаемся на шаг 1.
double GS(double k) {
// Assume that k < 1
double x = 0;
int iter = 0;
do {
// M_E is base of natural logarithm
double U = Uniform(0, 1 + k / M_E)
double W = Exponential(1)
if (U <= 1)
{
x = pow(U, 1.0 / k);
if (x <= W)
return x;
}
else
{
x = -log((1 - U) / k + 1.0 / M_E);
if ((1 - k) * log(x) <= W)
return x;
}
} while (++iter < 1e9); // excessive maximum number of rejections
return NAN; // shouldn't end up here
}
Алгоритм GF
Насколько мне известно, автор этого алгоритма, профессор Университета Северной Каролины Дж. С. Фишман, не стал опубликовывать свое достижение. Сам алгоритм работает для k > 1, однако среднее время его выполнения возрастает пропорционально sqrt(k), поэтому он эффективен только для k < 3. Алгоритм:
- Генерируем две независимых случайных величины E1 и E2 со стандартным экспоненциальным распределением.
- Если E2 < (k — 1) * (E1 — ln(E1) — 1), то возвращаемся назад на шаг 1.
- Возвращаем x = k * E1
Доказательство
Теорема. Пускай U — равномерно распределенная случайная величина на [0, 1] и W — экспоненциально распределенная случайная величина с плотностью 1 / lambda. Пусть:

Если g(W) >= U, то W имеет гамма-распределение с параметром lambda:
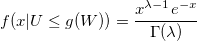
Доказательство. Функция плотности распределения W:

Таким образом,
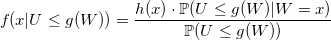
Так как U имеет равномерное распределение, то

если 0 < g(x) < 1. Тогда безусловная вероятность:
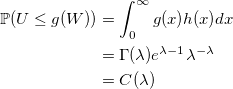
В результате, условная плотность вероятности:
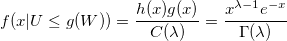
q.e.d.
Эффективность генератора обусловлена вероятностью того, что U <= g(W), которая равняется C(lambda). При больших значениях параметра \lambda, используя аппроксимацию Стирлинга, можно примерно рассчитать вероятность:
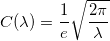
Алгоритм становится неэффективным при растущем lambda.

Если g(W) >= U, то W имеет гамма-распределение с параметром lambda:

Доказательство. Функция плотности распределения W:
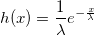
Таким образом,

Так как U имеет равномерное распределение, то

если 0 < g(x) < 1. Тогда безусловная вероятность:

В результате, условная плотность вероятности:
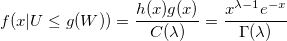
q.e.d.
Эффективность генератора обусловлена вероятностью того, что U <= g(W), которая равняется C(lambda). При больших значениях параметра \lambda, используя аппроксимацию Стирлинга, можно примерно рассчитать вероятность:

Алгоритм становится неэффективным при растущем lambda.
double GF(double k) {
// Assume that 1 < k < 3
double E1, E2;
do {
E1 = Exponential(1);
E2 = Exponential(1);
} while (E2 < (k - 1) * (E1 - log(E1) - 1));
return k * E1;
}
Алгоритм GO
Алгоритм Дитера и Аренса основан на асимптотической нормальности распределения при увеличении параметра, и поэтому более быстр для больших k. Он работает для k > 2.533, однако не столь эффективен как алгоритм Фишера для k < 3. Для начала нужно задать некоторые константы (зависящие только от k).
void setupConstants(double k) {
m = k - 1;
s_2 = sqrt(8.0 * k / 3) + k;
s = sqrt(s_2);
d = M_SQRT2 * M_SQRT3 * s_2;
b = d + m;
w = s_2 / (m - 1);
v = (s_2 + s_2) / (m * sqrt(k));
c = b + log(s * d / b) - m - m - 3.7203285;
}
double GO(double k) {
// Assume that k > 3
double x = 0;
int iter = 0;
do {
double U = Uniform(0, 1);
if (U <= 0.0095722652) {
double E1 = Exponential(1);
double E2 = Exponential(1);
x = b * (1 + E1 / d);
if (m * (x / b - log(x / m)) + c <= E2)
return x;
}
else {
double N;
do {
N = Normal(0, 1);
x = s * N + m; // ~ Normal(m, s)
} while (x < 0 || x > b);
U = Uniform(0, 1);
double S = 0.5 * N * N;
if (N > 0) {
if (U < 1 - w * S)
return x;
}
else if (U < 1 + S * (v * N - w))
return x;
if (log(U) < m * log(x / m) + m - x + S)
return x;
}
} while (++iter < 1e9);
return NAN; // shouldn't end up here;
}
Как и в случае предыдущих распределений — любая величина с гамма-распределением генерируется из стандартной умножением на параметр theta. Умея генерировать равномерное, нормальное, экспоненциальное и гамма-распределения, вы, скорее всего, с легкостью сможете получить большинство других распределений, благо они легко выражаются через вышеупомянутые.
Распределение Коши


Один из способов быстро получить случайную величину с распределением Коши — это взять две нормальные случайные величины и поделить друг на друга. Можно ли быстрее? Можно воспользоваться обычным методом инверсии, но он потребует вычисления тангенса. Это еще медленнее.

Или нет?
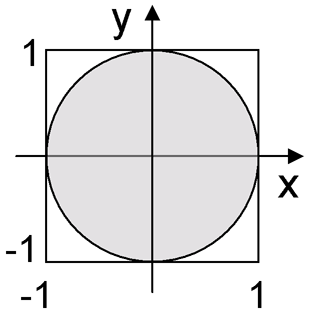
Помните полярный метод Джорджа Марсальи? Он позволял в преобразовании Бокса-Мюллера быстро получать синус или косинус равномерно распределенной случайной величины. Ровно таким же образом можно получить и тангенс. Генерируем две равномерно распределенные случайные координаты x и y на квадрате [-1, 1]x[-1, 1]. Если мы попали в круг с центром в (0, 0) и единичным радиусом — возвращаем x/y, иначе — генерируем x и y еще раз. Вероятность не попасть в круг, скажем, с раза третьего уже меньше чем 0.01.
double Cauchy(double x0, double gamma) {
double x, y;
do {
x = Uniform(-1,1);
y = Uniform(-1,1);
} while (x * x + y * y > 1.0 || y == 0.0);
return x0 + gamma * x / y;
}
Распределение Лапласа

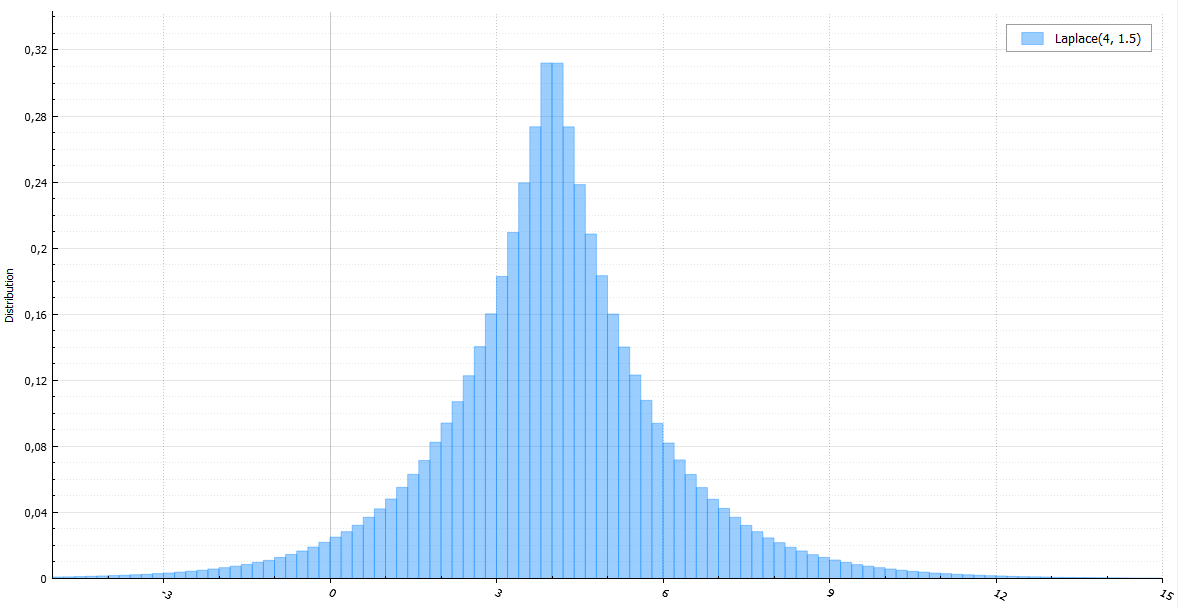
Распределение Лапласа — это то же экспоненциальное, только со случайным знаком.
double Laplace(double mu, double b) {
double E = Exponential(1.0 / b);
return mu + (((signed)BasicRandGenerator() > 0) ? E : -E);
}
Распределение Леви


Несмотря на то, как ужасно выглядит функция плотности распределения, сама случайная величина генерируется крайне просто и быстро:
double Levy(double mu, double c) {
double N = Normal(0, 1);
return mu + c / (N * N);
}
Распределение хи-квадрат

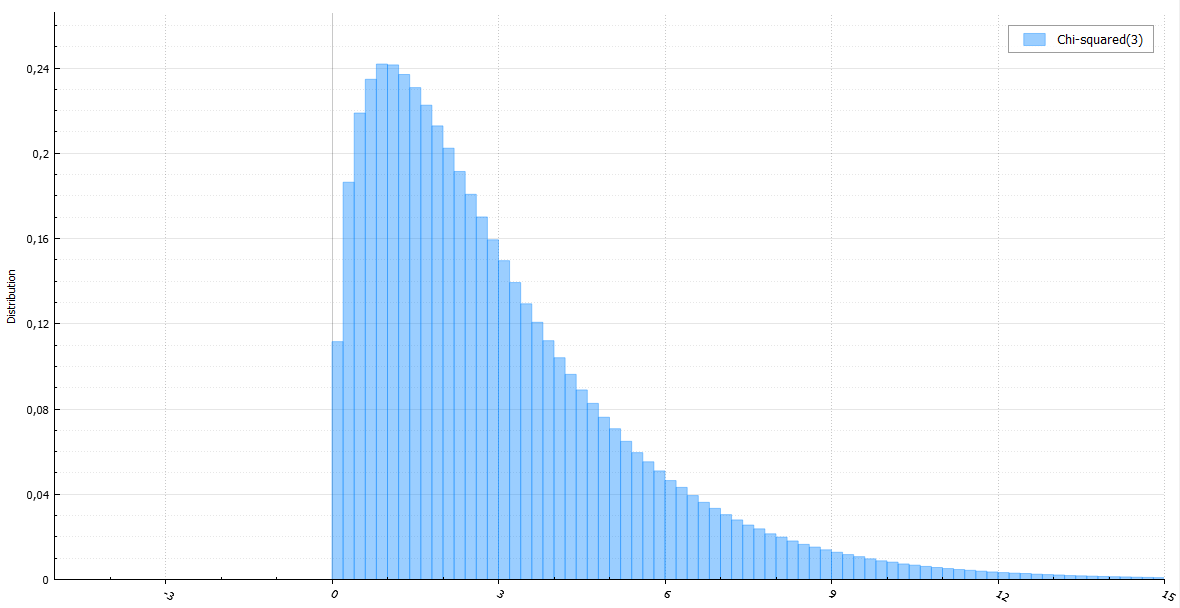
Как известно, случайная величина с распределением хи-квадрат с параметром k — это сумма квадратов k стандартных нормальных случайных величин. Менее известно, что при четном k это же и удвоенная сумма k/2 экспоненциальных случайных величин (или же распределение Эрланга). Из этого соотношения и происходит вышеупомянутый алгоритм GA2:
Доказательство
Этот факт легко доказать, используя характеристическую функцию — обратное преобразование Фурье функции плотности распределения:

У этой функции есть полезное свойство для суммы двух независимых случайных величин:
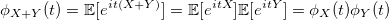
Пусть E — случайная величина с экспоненциальным распределением:

Тогда её характеристическая функция:
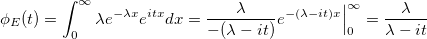
Нам нужно узнать распределение случайной величины равной удвоенной сумме стандартных экспоненциальных величин:
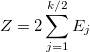
Если оно совпадает с распределением хи-квадрат, то его характеристическая функция:

Докажем это. Ранее было упомянуто также, что для экспоненциального распределения:

Используя это свойство, получаем:

q.e.d.

У этой функции есть полезное свойство для суммы двух независимых случайных величин:
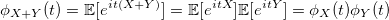
Пусть E — случайная величина с экспоненциальным распределением:

Тогда её характеристическая функция:

Нам нужно узнать распределение случайной величины равной удвоенной сумме стандартных экспоненциальных величин:

Если оно совпадает с распределением хи-квадрат, то его характеристическая функция:
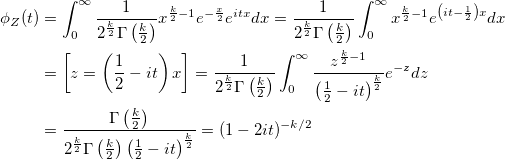
Докажем это. Ранее было упомянуто также, что для экспоненциального распределения:

Используя это свойство, получаем:

q.e.d.
double ChiSquared(int k) {
// ~ Gamma(k / 2, 2)
if (k >= 10) // too big parameter
return GO(0.5 * k);
double x = ((k & 1) ? GA2(0.5 * k) : GA1(k >> 1));
return x + x;
}
Из этого свойства следует примечательный факт: если выбирать точку на плоскости со случайными и нормальными координатами (x, y), то расстояние от (0,0) до этой точки будет распределено экспоненциально.
Логнормальное распределение


Люди, работающие с математическими моделями на финансовых рынках, о логнормальном распределении знают не понаслышке. Для логнормального, лог-Коши, лог-логистического распределений есть один простецкий способ — взять экспоненту. К сожалению, способа быстрее я не знаю, однако, возможно, существует способ генерировать подобные величины с помощью распределения Леви и/или распределения хи-квадрат. Посмотрите, как они похожи. А пока так:
double LogNormal(double mu, double sigma) {
return exp(Normal(mu, sigma));
}
Логистическое распределение

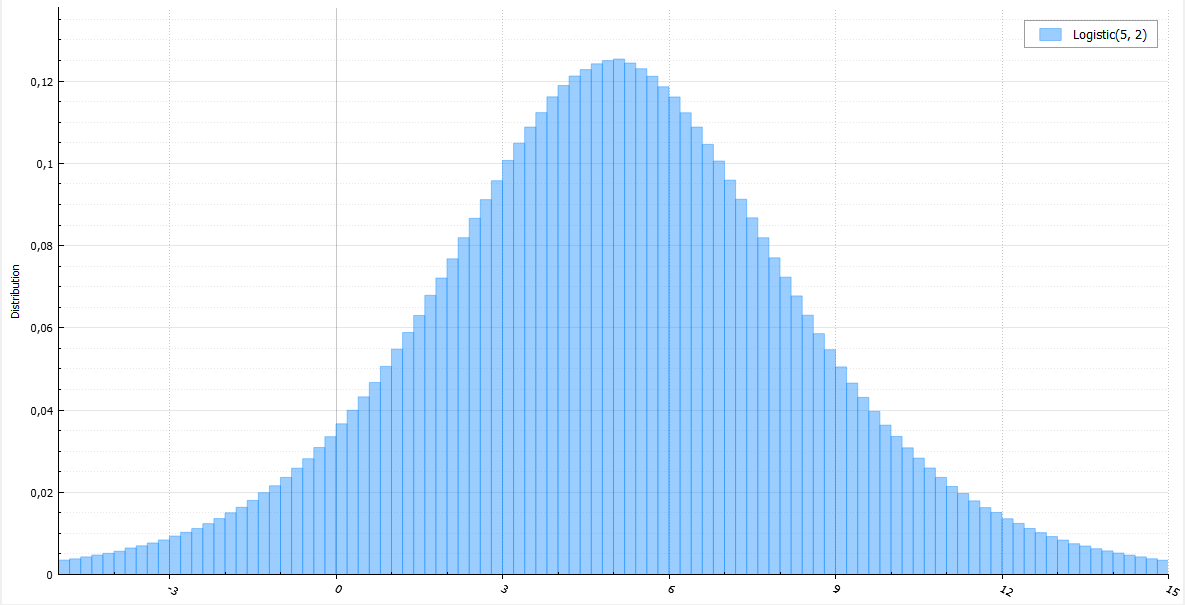
Логистическое распределение очень похоже на нормальное, но имеет более тяжелый хвост, генерируется довольно легко через стандартное равномерное распределение:
double Logistic(double mu, double s) {
return mu + s * log(1.0 / Uniform(0, 1) - 1);
}
Напоследок вкратце о не всегда быстрых, но очень простых алгоритмах для других популярных распределений:
double Erlang(int k, double l) {
return GA1(k) / l;
}
double Weibull(double l, double k) {
return l * pow(Exponential(1), 1.0 / k);
}
double Rayleigh(double sigma) {
return sigma * sqrt(Exponential(0.5));
}
double Pareto(double xm, double alpha) {
return xm / pow(Uniform(0, 1), 1.0 / alpha);
}
double StudentT(int v) {
if (v == 1)
return Cauchy(0, 1);
return Normal(0, 1) / sqrt(ChiSquared(v) / v);
}
double FisherSnedecor(int d1, int d2) {
double numerator = d2 * ChiSquared(d1);
double denominator = d1 * ChiSquared(d2);
return numerator / denominator;
}
double Beta(double a, double b) {
double x = Gamma(a);
return x / (x + Gamma(b));
}
Реализация этих и других генераторов на C++17