В наши дни, МКЭ — это наверное самый распространенный метод для решения широкого спектра прикладных инженерных задач. Исторически, он появился из механики, однако впоследствии был применен к всевозможным не механическим задачам.
Сегодня имеется большое разнообразие программных пакетов, таких как ANSYS, Abaqus, Patran, Cosmos, и т.д. Эти программные пакеты позволяют решать задачи строительной механики, механики жидкости, термодинамики, электродинамики и многие другие. Сама реализация метода, как правило считается достаточно сложной и объемной.
Здесь я хочу показать, что в настоящее время, используя современные инструменты, написание простейшего МКЭ расчетчика с нуля, для двумерной задачи плоско-напряженного состояния не является чем-то очень сложным и громоздким. Я выбрал этот вид задачи потому, что это был первый успешный пример применения метода конечных элементов. Ну и конечно он являются самым простым для реализации. Я собираюсь использовать линейный, трех-узловой элемент, так как это единственный плоский элемент, в случае которого не требуется численное интегрирования, как это будет показано ниже. Для элементов более высокого порядка, за исключением операции интегрирования (которая не совсем тривиальная, но при этом ее реализация достаточно интересная) идея абсолютно такая же.
Картинка для привлечения внимания:
Исторически сложилось так, что первое практическое применение МКЭ было в области механики, что существенно отразилось на терминологии и первых интерпретациях метода. В простейшем случае, суть метода может быть описана следующим образом: сплошная среда заменяется эквивалентной шарнирной системой, а решение статически неопределимых систем является хорошо известной и изученной проблемой механики. Эта упрощенная, инженерная трактовка способствовала широкому распространению метода, однако строго говоря, такое понимание метода является неправильным. Точное математическое обоснование метода было дано намного позже первых успешных применений метода, но это позволило расширить область применения для большего круга задач, не только из области механики.
Я не собираюсь описывать метод подробно, есть много литературы о нем, вместо этого я сосредоточусь на реализации метода. Потребуются минимальные знания механики, или того же сопромата. Также буду рад, отзывам людей не имеющих отношения к механики, была ли понятна хотя бы идея. Реализация метода будет на C++, однако я не буду использовать никакие сильно специфические особенности этого языка и надеюсь, что код будет понятен людям не знающим данный язык.
Так как это всего лишь пример реализации метода, чтобы не усложнять и оставить все в наиболее простом виде для понимания, я буду отдавать предпочтение краткости в ущерб многим принципам программирования. Это не пример по написанию хорошего, сопровождаемого и надежного кода, это пример по реализации МКЭ. Так что будет много упрощений, чтобы сконцентрироваться на основной цели.
Прежде чем приступить к самой методу, давайте выясним, в каком виде мы будет представлять входные данные. Рассматриваемый объект должен быть разделен на большое количество мелких элементов, в нашем случае — треугольников. Таким образом, мы заменяем непрерывную среду на набор узлов и конечных элементов, образующих сетку. На рисунке ниже, показан пример сетки с пронумерованными узлами и элементами.

На рисунке мы видим девять узлов и восемь элементов. Для описания сетки, нужно два списка:
В списке элементов, каждый элемент определяется множеством индексов узлов, которые образует элемент. В нашем случае, у нас есть только треугольные элементы, так что мы будем использовать только три индекса для каждого элемента.
В качестве примера, для сетки показанной выше, мы будет иметь следующие списки:
Список узлов:
Список элементов:
Стоит отметить, что есть несколько способов задать один и тот же элемент. Индексы узлов можно перечислять по часовой стрелке или против часовой стрелки. Обычно используется перечисление против часовой стрелки, поэтому мы будем предполагать, что все элементы заданы именно таким образом.
Давайте создадим некий входной файл с полным описанием задачи. Чтобы избежать путаницы и не усложнять, лучше использовать индексацию, которая начинается с нуля, а не с единицы, так как в C/C ++ массивы индексируются с нуля. Для первого тестового входного файла, мы создадим самую простую сетку из возможных:

Пусть первая строка будет описание свойств материала. Например, для стали, коэффициент Пуассона ν = 0,3 и модуль Юнга Е = 2000 МПа:
Затем следует строка с количеством узлов и затем сам список узлов:
Затем следует строка с количеством элементов, далее список элементов:
Теперь, нам нужно задать закрепления, или как говорят, условия на границе первого рода. В качестве таких граничных условий мы будем фиксировать перемещения узлов. Фиксировать можно перемещения по осям независимо друг от друга, т.е. мы можем запретить перемещения по оси x или по оси y или по обоим сразу. В общем случае, можно задавать некоторое начальное перемещение, однако мы ограничимся лишь нулевым начальным перемещением. Таким образом, у нас будет список узлов с заданным типом ограничений на перемещение. Тип ограничения будут указаны номером:
Первая строка определяет количество ограничений:
Затем, мы должны задать нагрузки. Мы будем работать только с узловыми силами. Строго говоря, узловые силы не должны рассматриваться как силы в общем смысле этого слова, я расскажу об этом позже, но сейчас давайте думать о них просто как о силах действующих на узел. Нам нужен список с индексами узлов и соответствующими векторами сил. Первая строка определяет количество приложенных сил:
Можно легко видеть, что рассматриваемая задача, это тело квадратной формы, низ которого закреплен, а на верхнюю грань действуют растягивающие усилия.

Входной файл целиком:
Перед тем, как приступить к написанию кода, я хотел бы рассказать о математической библиотеке — Eigen. Это зрелая, надежная и эффективная библиотека, которая обладает очень чистым и выразительным API. В ней есть множество compile-time оптимизаций, библиотека способна выполнять явную векторизацию и поддерживает SSE 2/3/4, ARM и NEON инструкции. Как по мне, эта библиотека замечательна хотя бы тем, что позволяет реализовывать сложные математические вычисления кратким и выразительным образом.
Я хотел бы сделать краткое описание части API Eigen, которое мы будем использовать далее. Те читатели, которые знакомы с этой библиотекой, могут пропустить этот раздел.
Есть два типа матриц: плотная и разреженные. Мы будем использовать оба типа. В случае с плотной матрицей, все элементы находятся в памяти, в порядке следования индексов, поддерживаются как column-major (дефолтный) так и raw-major размещение. Этот тип матриц хорош для относительно небольших матриц или матриц с небольшим количеством нулевых элементов. Разреженные матрицы хороши для хранения больших матриц с небольшим количеством ненулевых элементов. Мы будем использовать разреженную матрицу для глобальной матрицы жесткости.
Для использования плотных матриц нам нужно будет включить заголовок <Eigen/Dense>. Есть два основных типа плотных матриц: с фиксированным и с динамическим размером. Матрица с фиксированным размером, это такая матрица, размер которой известен во время компиляции. В случае с матрицей динамического размера, ее размер может быть задан на этапе выполнения кода, более того, размер динамической матрицы можно даже изменять налету. Конечно, нужно отдавать предпочтение матрицам с фиксированным размером везде, где это возможно. Память под динамические матрицы выделяется в куче, также неизвестный размер матрицы ограничивает оптимизации, которые компилятор может сделать. Фиксированные матрицы могут быть выделены в стеке, компилятор может развернуть циклы и многое другое. Стоит отметить, что также возможен смешанный тип, когда у матрицы фиксируется количество строк, но количество столбцов динамично, или наоборот.
Матрицы фиксированного размера могут быть определены следующим образом:
Где m — float матрица c фиксированный размеров 3 × 3. Также можно использовать следующие предопределенные типы:
Есть немного больше предопределенных типов, эти являются основными. Цифра обозначает размерность квадратной матрицы и буква обозначает тип элемента матрицы: i — целое число, f — число с плавающей точкой одинарной точности, d — число с плавающей точкой двойной точности.
Для векторов нету отдельного типа, вектора такие-же матрицы. Вектор-столбец (иногда в литературе встречаются векторы-строки, приходится уточнять), можно объявить следующим образом:
Или можно использовать один из предопределенных типов (обозначения те же, что и для матриц):
Для быстрого ознакомления, я написал следующий пример:
Вывод:
Для более подробной информации лучше обратиться к документации.
Разреженная матрица является немного более сложным, типом матрицы. Основная идея не хранить всю матрицу в памяти как есть, а хранить только ненулевые элементы. Довольно часто в практических задачах встречаются большие матрицы с малым количеством ненулевых элементов. При сборке глобальной матрицы жесткости в МКЭ модели, количество ненулевых элементов может быть меньше, чем 0,1% от общего числа элементов.
Для современных пакетов МКЭ не проблема решить задачу с сотней тысяч узлов, причем на вполне обычном современном PC. Если мы попытаемся выделить место для хранения глобальной матрицы жесткости, мы столкнемся со следующей проблемой:
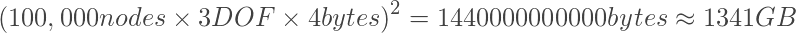
Размер памяти, необходимый для хранения матрицы огромный! Разреженная матрица потребуется в 10000 раз меньшее количество памяти.
Разреженные матрицы используют память более эффективно, так как хранят только ненулевые элементы. Разреженные матрицы могут быть представлены двумя способами: сжатым и несжатым. В несжатом виде легко добавить или удалить элемент из матрицы, но такой вид представления не является оптимальным с точки зрения использования памяти. Eigen, при работе с разреженной матрицей, использует своеобразное сжатое представление, несколько более оптимизированное для динамического добавления/удаления элементов. Eigen также умеет конвертировать такую матрицу в сжатый вид, более того он это делает прозрачно, делать это в явном виде не нужно. Большинство алгоритмов требуют сжатый вид матрицы, и применение любого из этих алгоритмов автоматически преобразует матрицу в сжатый вид. И наоборот, добавление/удаление элемента автоматически конвертирует матрицу в оптимизированное представление.
Как мы можем задать матрицу? Хороший способ это сделать — использовать так называемые Triplets. Это структура данных, причем это шаблонный класс, который представляет собой один элемент матрицы в комбинации с индексами, определяющими его положение в матрице. Мы можем задать разреженную матрицу непосредственно из вектора triplets.
Например, мы имеем следующую разреженную матрицу:
Первое, что мы должны сделать, это включить соответствующий заголовок библиотеки Eigen: <Eigen/Sparse>. Затем, мы объявляем пустую разреженную матрицу размерности 5х5. Далее, мы определяем вектор triplets и заполняем его значениями. Конструктор triplet'а принимает следующие аргументы: i-индекс, j-индекс, значение.
Вывод будет следующим:
Для хранения данных, которые мы собираемся читать из входного файла, а также промежуточных данных, мы должны объявить свои структуры. Простейшая структура данных описывающая конечный элемент показана ниже. Она состоит из массива трех элементов, которые хранят индексы узлов образующих конечный элемент, а также матрицы В. Данная матрица называемый градиентной матрицей и мы вернемся к ней позже. О методе CalculateStiffnessMatrix также будет рассказано далее.
Еще одна простая структура которая нам понадобится — это структура для описания закреплений. Это простая структура состоящая из перечисляемого типа, который определяет тип ограничения, и индекса узла на который накладывается ограничение.
Чтобы не усложнять, давайте определим некоторые глобальные переменные. Создавать какие-либо глобальные объекты — это всегда плохая идея, но для этого примера вполне допустимо. Нам понадобятся следующие глобальные переменные:
В коде, мы определим их следующим образом:
Перед чем как что-то читать, мы должны знать откуда читать и куда писать вывод. В начале main функции проверим количество входных аргументов, обращаю внимание, что первый аргумент всегда путь к исполняемому файлу. Таким образом, у нас должно быть три аргумента, пусть второй будет путь к входному файлу, а третий — путь к файлу с выводом. Для работы с вводом/выводом, для конкретного случая удобнее всего использовать файловые потоки из стандартной библиотеки.
Первое, что мы делаем — создаем потоки для ввода/вывода:
В первой строке входного файла находятся свойства материала, прочитаем их:
Этого достаточно, чтобы построить матрицу упругости изотропного материала для плоско-напряженного состояния, которая определена следующим образом:


Откуда взялись эти выражения? Они легко получаются из закона Гука в общем виде, действительно, мы можем найти выражение для матрицы D из следующих соотношений:
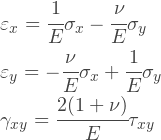
Стоит отметить, что плоско-напряженное состояние означает, что σZ равно нулю, но не εZ. Плоско-напряженная модель хорошо подходит для решения ряда инженерных задач, где рассматриваются плоские структуры и все силы действуют в плоскости. Во времена, когда расчеты объемных задач были слишком дорогими, множество задач удавалось свести к плоским, жертвуя при этом точностью.
При плоско-напряженном состоянии, ничто не мешает телу деформироваться в направлении нормали к его плоскости, поэтому деформация εZ в общем случае не равна нулю. Она не появляется в уравнениях выше, но может быть легко получена из следующего соотношения, учитывая что напряжение σZ равно нулю:
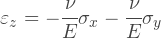
У нас есть все исходные данные чтобы задать матрицу упругости, давайте сделаем это:
Далее, мы читаем список с координатами узлов. Сначала читаем количество узлов, затем задаем размер динамических векторов х и у. Далее, мы просто читать координаты узлов в цикле, строка за строкой.
Затем, мы читаем список элементов. Все то-же самое, читаем количество элементов, а затем индексы узлов для каждого элемента:
Далее, читаем список закреплений. Все то же самое:
Вы могли заметить static_cast, он нужен чтобы преобразовать int тип, в объявленный нами ранее перечисляемый тип для закреплений.
Наконец, нужно прочитать список нагрузок. Есть одна особенность связанная с нагрузкой, из-за которой мы будем представлять действующие нагрузки в виде вектора размерности двойного количества узлов. Причина, почему мы делаем так, будет объяснена чуть позже. Рисунок ниже, иллюстрирует этот вектор нагрузки:

Таким образом, для каждого узла, у нас есть два элемента в векторе нагрузки, которые представляют х и у компоненты усилия. Таким образом, х-компонента усилия в определенном узле будет храниться в элементе с индексом id = 2 * node_id + 0, а у-составляющая усилия для этого узла будет храниться в элементе с индексом id = 2 * node_id + 1.
Сначала зададим размер вектора приложенных усилий вдвое больший, чем количество узлов, затем обнулим вектор. Читаем количество внешних сил и читаем их значения строка за строкой:
Мы рассматриваем геометрически линейную систему с бесконечно малыми перемещениями. Более того, мы предполагаем, что деформирование происходит упруго, т.е. деформации являются линейной функцией напряжений (закон Гука). Из основ строительной механики можно показать, что перемещение каждого узла является линейной функцией приложенных сил. Таким образом, мы можем говорить, что у нас есть следующая система линейных уравнений:

Где: К — матрица жесткости; δ — вектор перемещений; R — вектор нагрузок, то есть вектор внешних сил. Эту систему линейных уравнений часто называют ансамблем, так как она представляет суперпозицию матриц жесткости каждого элемента, как это будет показано ниже.
Вектор перемещений, для двумерных проблем может быть задан следующим образом:

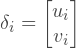
Где: ui и vi — u-компонента и v-компонента перемещения i-го узла.
Вектор внешних сил:


Где: Rxi и Ryi — х-компонента и y-компонента внешнего усилия приложенного к i-му узлу.
Как мы видим, каждый элемент вектора перемещения и вектора нагрузок является двумерным вектором. Вместо этого, мы можем определить эти векторы следующим образом:

То есть фактически то же самое, но это упрощает представление этих векторов в коде. Это объяснение, почему мы ранее задали вектор нагрузки таким своеобразным способом.
Как построить матрицу жесткости? Суть глобальной матрицы жесткости есть суперпозиция матриц жесткости каждого элемента. Если мы рассмотрим один элемент отдельно от остальных, то мы можем определить такую-же матрицу жесткости, но только для данного элемента. Эта матрица определяет соотношения между перемещениями узлов и узловыми силами. Например для 3-узлового элемента:

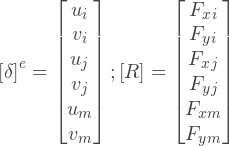
Где: [k]е — матрица жесткости e-го элемента; [δ]е — вектор перемещений узлов е-го элемента; [F]е — вектор узловых сил е-го элемента; i, j, m — индексы узлов элемента.
Что произойдет, если один узел будет разделен между двумя элементами? Прежде всего, поскольку это все тот-же узел, перемещение соответственно не будет зависеть от того в составе какого элемента мы рассматриваем этот узел. Вторым важным следствием является то, что если суммировать все узловые силы от каждого элемента в этом узле, то результат будет равен внешней силе, иными словами — нагрузке.
Сумма всех узловых сил в каждом узле равна сумме внешних сил в этом узле, это следует из принципа равновесия. Несмотря на то, что данное утверждение может показаться вполне логичным и справедливым, на самом деле все немного сложнее. Такая формулировка не является точной, потому что узловые силы не являются силами в общем смысле этого слова, и выполнение условий равновесия для них вовсе не очевидное условие. Несмотря на то, что утверждение все же верное, оно использует механический принцип, чем ограничевает применение метода. Существует более строгое, математическое обоснование МКЭ с позиций минимизации потенциальной энергии, что позволяет распространить метод на более широкий спектр задач.
На мой взгляд, об узловых силах лучше думать как о неких обобщенных силах, в представлении Лагранжевой механики. Дело в том, что перемещение узла, на самом деле является обобщенным перемещением, так как оно однозначно характеризует поле перемещений внутри элемента. Каждую компоненту перемещения узла можно трактовать как обобщенную координату, следовательно и силы, действуют не в точке узла, а по границе элемента (или по объему для объемных сил), причем действуют именно на том перемещении, которое характеризует данный узел.
Если просуммировать все уравнения для каждого узла, меж-элементные узловые силы уйдут. С правой стороны уравнения останутся только внешние силы — нагрузки. Таким образом, учитывая этот факт, мы можем написать:

Рисунок ниже иллюстрирует вышеприведенное выражение:

Для построения глобальной матрицы жесткости, нам понадобится вектор triplets. В цикле, мы пройдемся по каждому элементу и заполним этот вектор значениями матриц жесткости полученными от каждого элемента:
Где std::vector<Eigen::Triplet<float> > — вектор triplets; CalculateStiffnessMatrix — метод класса элемента, который заполняет вектор triplets.
Как уже упоминалось ранее, мы можем построить глобальную разреженную матрицу прямо из вектора triplets:
Мы выяснили, как собрать глобальную матрицу жесткости (ансамбль) из матриц элементов, Осталось выяснить как получить матрицу жесткости элемента.
Давайте начнем с интерполяции перемещений внутри элемента основываясь на перемещениях его узлов. Если перемещения узлов заданы, то перемещение в любой точке элемента можно представить как:

Где [N] представляет собой матрицу функций координат (х, у). Эти функции называются функциями формы. Каждую компоненту перемещения, u и v можно интерполировать независимо, тогда уравнение выше, можно переписать в следующем виде:
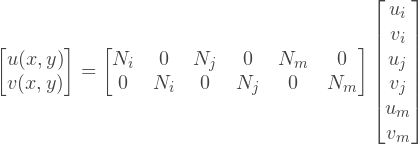
Или можно записать в раздельной форме:
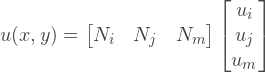

Как получить инерполирующую функцию? Для простоты, давайте рассмотрим скалярное поле. В случае трех-узлового, линейного элемента, функция интерполяции является линейной. Интерполяционное выражение мы будем искать в следующем виде:

Если значения f в узлах известны, то мы можем задать систему из трех уравнений:
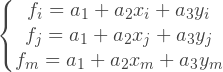
Или в матричной форме:

Из этой системы уравнений, мы можем найти неизвестный вектор коэффициентов для интерполирующего выражения:

Введем обозначение

Наконец, получим интерполяционное выражение:

Возвращаясь к перемещениям, мы можем сказать, что:


Тогда, функции формы будут иметь вид:

Зная поле перемещений, мы можем найти поле деформаций, по соотношениям из теории упругости:

Теперь мы можем заменить u и v, на функции формы:
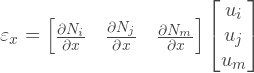
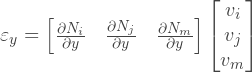

Или мы можем написать то же самое в комбинированной форме:

Матрица с правой стороны, обычно обозначается как матрица В, так называемая градиентная матрица.

Чтобы найти матрицу В, мы должны найти все частные производные функций формы:


В случае с линейным элементом, мы видим, что частные производные функций формы на самом деле являются константами, что сэкономит нам множество усилий, как это будет показано далее. Умножив вектор-строку с константами на обратную матрицу C получим:

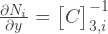
Теперь мы можем рассчитать B матрицу. Чтобы построить матрицу C, сначала зададим векторы координат узлов:
Затем, мы можем построить матрицу С из трех строк:
Затем мы вычисляем обратную матрицу С и собираем матрицу B:
Как мы уже упоминали ранее, соотношение между напряжением и деформацией можно записать с помощью матрицы упругости D:

Таким образом, подставляя выражение выше в соотношение для деформаций, получим:

Здесь мы видим, что напряжения, как и деформации являются константами внутри элемента. Это особенность линейных элементов. Однако, для элементов более высоких порядков, неразрывность напряжений также не выполняется. При увеличении числа элементов, эти разрывы должны уменьшаться что является критерием сходимости. На практике, обычно вычисляют среднее значение деформаций для каждого узла, однако в нашем случае мы оставим все как есть.
Для того, чтобы перейти к матрице жесткости, мы должны обратиться к виртуальной работе. Скажем, у нас есть некие виртуальные перемещения в узлах элемента: d[δ]e
Виртуальные перемещения должны пониматься как любые бесконечно малые перемещения, которые могут произойти. Мы знаем, что в случае с нашей задачей, существует только одно решение и только один набор перемещений будет иметь место, но здесь мы рассматриваем все немного под другим углом. Другими словами, мы берем все бесконечно малые перемещения которые разрешены кинематически, а затем находим те единственные, которые удовлетворяют физический закон.
Для этих виртуальных перемещений, виртуальная работа узловых сил будет:

Виртуальная работа внутренних напряжений в единице объема для тех-же виртуальный перемещений:
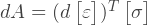
Или:

Подставляя уравнение для напряжений, мы получим:

Из закона сохранения энергии, виртуальная работа внешних сил должна быть равна сумме работы внутренних напряжений по объему элемента:
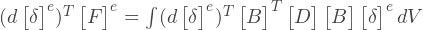
Так, как это соотношение должно быть справедливо для любого виртуального перемещения, мы можем разделить обе части уравнения на виртуальное перемещение:

Узловые перемещения можно вынести за интеграл, так как они постоянны внутри элемента. Теперь мы видим, что интеграл является коэффициентом пропорциональности между узловыми перемещениями и узловыми силами, это означает, что интеграл представляет собой матрицу жесткости:
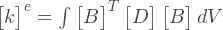
Для линейного элемента, как мы получили ранее, матрица В является константой. Если свойства материала также постоянны, то интеграл становится тривиальным:
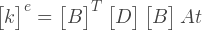
Где A — площадь элемента, t — толщина элемента. Из свойств треугольника, его площадь может быть получена как половина детерминанта матрицы С:

В конце концов, мы можем записать следующий код для вычисления матрицы жесткости:
Здесь я опустил толщину, будем считать что она у нас единична. Обычно, на практике используют следующую систему единиц: МПа, мм2. В этом случае, если мы задаем модуль упругости в мегапаскалях, а размеры в миллиметрах, то толщина будет один миллиметр. Если нужна другая толщина, то ее легко можно внести в модуль упругости. В более общем случае, лучше всего задавать толщину поэлементно или даже для каждого узла.
Метод CalculateStiffnessMatrix целиком:
В конце метода, после вычисления матрицы жесткости, заполняется вектор Triplets. Каждый Triplet создается используя массив индексов узлов элемента, чтобы определить его положение в глобальной матрице жесткости. На всякий случай, подчеркну, что у нас есть два набора индексов, один локальный — для матрицы элемента, другой глобальный — для ансамбля.
Полученная система линейных уравнений не может быть решена до тех пор, пока мы не зададим закрепления. Чисто с механической точки зрения, незакрепленная система может совершать любые большие перемещения, а под действием внешних сил и вовсе перейдет в движение. Математически, это приведет к тому, что полученная СЛАУ не является линейно независимой, а следовательно не имеет единственного решения.
Перемещения некоторых узлов должны быть установлены в ноль или в некоторую заранее заданную величину. В простейшем случае, давайте рассмотрим только закрепления узлов, без начальных смещений. На самом деле это означает, что мы удаляем некоторые уравнения из системы. Но изменение количества уравнения системы на лету, не тривиальная задача. Вместо этого можно воспользоваться следующим трюком.
Скажем, мы имеем следующую систему уравнений:

Чтобы закрепить узел, соответствующий элемент матрицы должен быть установлен в 1, и все элементы в строке и столбце содержащие этот элемент должны быть установлены в ноль. Так же не должно быть никаких внешних сил, действующих на закрепленный узел в направлении в котором действует ограничение. Уравнение с этим узлом, явно даст нулевое смещение для этого узла, а нули в соответствующем столбце исключат это смещение из других уравнений. Скажем, мы хотим закрепить нулевой узел в направлении оси х, и закрепить первый узел в направлении оси у:

Чтобы выполнить эту операцию, сначала определим индексы уравнений, которые мы собираемся исключать из СЛАУ. Чтобы это сделать, мы в цикле пройдемся по списку закреплений и соберем вектор индексов. Затем, перебирая все ненулевые элементы матрицы жесткости вызываем функцию SetConstraints. Ниже приведена функция ApplyConstraints:
Функция SetConstraints проверяет, является ли элемент матрицы жесткости частью исключенного уравнения, и если это так, то он устанавливает его равным нулю или единице в зависимости от того, находится ли элемент на диагонали или нет:
Далее, мы просто вызываем ApplyConstraints и передаем ей в качестве аргументов глобальную матрицу жесткости и вектор закреплений:
Библиотека Eigen имеет в наличии различные решатели разреженных линейных уравнений, мы будем использовать SimplicialLDLT, который является быстрым прямым решателем. Для демонстрационных целей, мы будем выводить исходную матрицу жесткости и вектор нагрузки, а затем выводить результат решения — вектор перемещений.
Разумеется, вывод матрицы имеет смысл только для нашего тестового примера, содержащего всего два элемента.
Как мы уже видели раньше, мы можем перейти от перемещений к деформациям а далее к напряжениям:

Однако, мы получаем вектор напряжений, который в теории упругости вообще говоря представляет собой симметричный тензор второго ранга:

Как известно, непосредственно элементы тензора зависят от системы координат, однако само физическое состояние конечно не зависит. Поэтому для анализа лучше перейти как какой либо инвариантной величине, лучше всего к скалярной. Таким инвариантом являются напряжения по Мизесу:
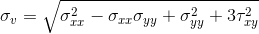
Эта скалярная величина, позволяет оценить напряжения при сложно-напряженном состоянии, так как если бы мы имели дело с одноосным напряженным состоянием. Данный критерий не идеален, но в большинстве случаем, для статического анализа дает более менее правдоподобную картину, поэтому он чаще всего используется на практике.
Теперь мы в цикле пройдемся по всем элементам, и расчитаем напряжения по Мизесу для каждого элемента:
На этом написание нашего простейшего МКЭ расчетчика можно считать законченным. Посмотрим, какой вывод мы получим для нашей тестовой задачи:
Мы видим, что закрепления мы задали верно, деформации закрепленных узлов в соответствующих направлениях равны нулю. Деформации верхних узлов направлены вверх, в соответствии с растягивающим усилием. Деформации в x-направлении, для правой пары узлов составляют величину 0.0003, что есть 0.3 часть от деформаций верхних узлов в y-направлении, что является эффектом Пуассона. Результат расчета полностью согласуется с ожиданиями, поэтому можно переходить к задачам поинтереснее.
Запустим утилиту cloc:
Как видим, всего ничего — 171 строчка кода.
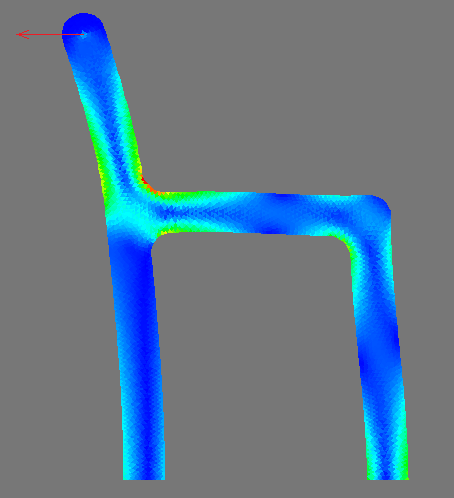
Для визуализации результатов расчета, был написан скрипт на python, который рисует недеформированный и деформированный меш с полем напряжений. К сожалению, я не знаю как сделать градиентную заливку с помощью PIL, поэтому напряжения внутри элемента отображаются как сплошная константная заливка. Abaqus умеет делать визуализацию и в таком виде, что хоть и выглядит менее красиво, за то ближе к правде.
Тестовая задача:

Для получения сеток посложнее, была использована бесплатная студенческая версия Abaqus. Для конвертации входного файла Abaqus'а был написан еще один скрипт. Правда задавать закрепления и внешние нагрузки все равно придется вручную.
Здесь мы видим полосу с отверстием, низ которой закреплен, а к верхней кромке приложено растягивающее усилие:

Абстрактный элемент конструкции, просто для красоты. Низ конструкции закреплен, а на верхнюю выступающую часть приложена сконцентрированая сила, которую я нарисовал уже поверх картинки:

Еще один пример с полосой с отверстием, на этот раз рассмотрена только четверть конструкции в силу симметрии. Левая граница закреплена по оси x, нижняя — по оси y. Максимальное полученное напряжение: 3.05152. Данная величина, несмотря на грубость сетки (а может и благодаря ей), достаточно близка к теоретическому значению — 3.

Та-же задача, но решенная в Abaqus. Как видим максимальное напряжение — 3.052, что полностью совпадает с нашим результатом. Такое точное совпадение в принципе не мудрено, так как практически, для треугольного элемента трудно сделать что-то каким-то своим способом, так чтобы результат отличался. Для элементов более высокого порядка у меня к сожалению такого 100%-го совпадения не получилось, что может быть объяснено разной реализацией численного интегрирования.

Весь исходный код, включая примеры доступен на github'е.
Честно говоря, за кадром осталось достаточно много. Но статья оказалась и так раздута, поэтому думаю на этом можно остановиться.
Не вошло (а хотелось):
Я думаю, что многие могут справедливо заметить, что в современных математических пакетах, таких как MATLAB есть инструменты для работы с МКЭ, и в принципе нет необходимости что либо писать на С++. Однако, здесь я все же хотел показать минимальную реализацию, с минимумом зависимостей, т.е. без использования сторонних инструментов. За исключением математической библиотеки конечно, но думаю, что все использованные функции для читателей должны быть предельно прозрачны.
P.S. Статья большая, уверен опечаток много, пожалуйста в личку.
Сегодня имеется большое разнообразие программных пакетов, таких как ANSYS, Abaqus, Patran, Cosmos, и т.д. Эти программные пакеты позволяют решать задачи строительной механики, механики жидкости, термодинамики, электродинамики и многие другие. Сама реализация метода, как правило считается достаточно сложной и объемной.
Здесь я хочу показать, что в настоящее время, используя современные инструменты, написание простейшего МКЭ расчетчика с нуля, для двумерной задачи плоско-напряженного состояния не является чем-то очень сложным и громоздким. Я выбрал этот вид задачи потому, что это был первый успешный пример применения метода конечных элементов. Ну и конечно он являются самым простым для реализации. Я собираюсь использовать линейный, трех-узловой элемент, так как это единственный плоский элемент, в случае которого не требуется численное интегрирования, как это будет показано ниже. Для элементов более высокого порядка, за исключением операции интегрирования (которая не совсем тривиальная, но при этом ее реализация достаточно интересная) идея абсолютно такая же.
Картинка для привлечения внимания:
Исторически сложилось так, что первое практическое применение МКЭ было в области механики, что существенно отразилось на терминологии и первых интерпретациях метода. В простейшем случае, суть метода может быть описана следующим образом: сплошная среда заменяется эквивалентной шарнирной системой, а решение статически неопределимых систем является хорошо известной и изученной проблемой механики. Эта упрощенная, инженерная трактовка способствовала широкому распространению метода, однако строго говоря, такое понимание метода является неправильным. Точное математическое обоснование метода было дано намного позже первых успешных применений метода, но это позволило расширить область применения для большего круга задач, не только из области механики.
Я не собираюсь описывать метод подробно, есть много литературы о нем, вместо этого я сосредоточусь на реализации метода. Потребуются минимальные знания механики, или того же сопромата. Также буду рад, отзывам людей не имеющих отношения к механики, была ли понятна хотя бы идея. Реализация метода будет на C++, однако я не буду использовать никакие сильно специфические особенности этого языка и надеюсь, что код будет понятен людям не знающим данный язык.
Так как это всего лишь пример реализации метода, чтобы не усложнять и оставить все в наиболее простом виде для понимания, я буду отдавать предпочтение краткости в ущерб многим принципам программирования. Это не пример по написанию хорошего, сопровождаемого и надежного кода, это пример по реализации МКЭ. Так что будет много упрощений, чтобы сконцентрироваться на основной цели.
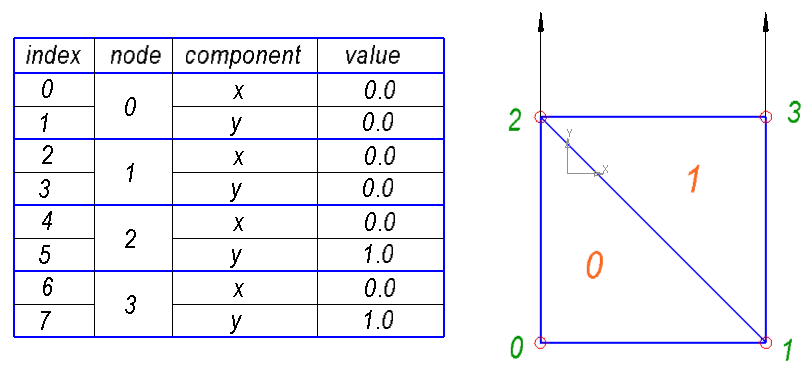
Входные данные
Прежде чем приступить к самой методу, давайте выясним, в каком виде мы будет представлять входные данные. Рассматриваемый объект должен быть разделен на большое количество мелких элементов, в нашем случае — треугольников. Таким образом, мы заменяем непрерывную среду на набор узлов и конечных элементов, образующих сетку. На рисунке ниже, показан пример сетки с пронумерованными узлами и элементами.
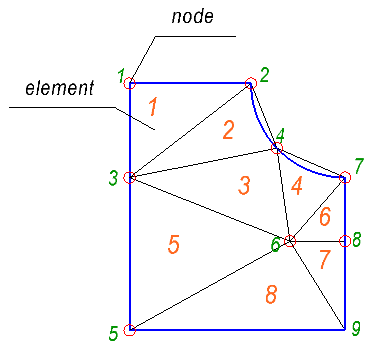
На рисунке мы видим девять узлов и восемь элементов. Для описания сетки, нужно два списка:
- Список узлов, который определяет координаты каждого узла.
- Список элементов.
В списке элементов, каждый элемент определяется множеством индексов узлов, которые образует элемент. В нашем случае, у нас есть только треугольные элементы, так что мы будем использовать только три индекса для каждого элемента.
В качестве примера, для сетки показанной выше, мы будет иметь следующие списки:
Список узлов:
0.000000 31.500000
15.516667 31.500000
0.000000 19.489759
18.804134 23.248226
0.000000 0.000000
20.479981 11.365822
27.516667 19.500000
27.516667 11.365822
27.516667 0.000000
Список элементов:
1 3 2
2 3 4
4 6 7
4 3 6
7 6 8
3 5 6
6 5 9
6 9 8
Стоит отметить, что есть несколько способов задать один и тот же элемент. Индексы узлов можно перечислять по часовой стрелке или против часовой стрелки. Обычно используется перечисление против часовой стрелки, поэтому мы будем предполагать, что все элементы заданы именно таким образом.
Давайте создадим некий входной файл с полным описанием задачи. Чтобы избежать путаницы и не усложнять, лучше использовать индексацию, которая начинается с нуля, а не с единицы, так как в C/C ++ массивы индексируются с нуля. Для первого тестового входного файла, мы создадим самую простую сетку из возможных:
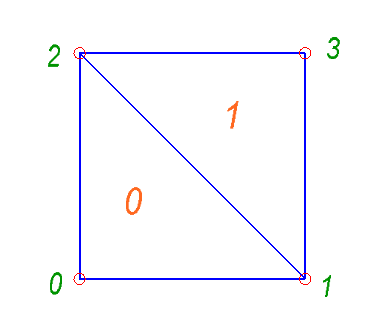
Пусть первая строка будет описание свойств материала. Например, для стали, коэффициент Пуассона ν = 0,3 и модуль Юнга Е = 2000 МПа:
0.3 2000Затем следует строка с количеством узлов и затем сам список узлов:
4
0.0 0.0
1.0 0.0
0.0 1.0
1.0 1.0
Затем следует строка с количеством элементов, далее список элементов:
2
0 1 2
1 3 2
Теперь, нам нужно задать закрепления, или как говорят, условия на границе первого рода. В качестве таких граничных условий мы будем фиксировать перемещения узлов. Фиксировать можно перемещения по осям независимо друг от друга, т.е. мы можем запретить перемещения по оси x или по оси y или по обоим сразу. В общем случае, можно задавать некоторое начальное перемещение, однако мы ограничимся лишь нулевым начальным перемещением. Таким образом, у нас будет список узлов с заданным типом ограничений на перемещение. Тип ограничения будут указаны номером:
- 1 — запрещено перемещение в направлении оси x
- 2 — запрещено перемещение в направлении оси y
- 3 — запрещено перемещение в обоих, х и у направлениях
Первая строка определяет количество ограничений:
2
0 3
1 2
Затем, мы должны задать нагрузки. Мы будем работать только с узловыми силами. Строго говоря, узловые силы не должны рассматриваться как силы в общем смысле этого слова, я расскажу об этом позже, но сейчас давайте думать о них просто как о силах действующих на узел. Нам нужен список с индексами узлов и соответствующими векторами сил. Первая строка определяет количество приложенных сил:
2
2 0.0 1.0
3 0.0 1.0
Можно легко видеть, что рассматриваемая задача, это тело квадратной формы, низ которого закреплен, а на верхнюю грань действуют растягивающие усилия.

Входной файл целиком:
0.3 2000
4
0.0 0.0
1.0 0.0
0.0 1.0
1.0 1.0
2
0 1 2
1 3 2
2
0 3
1 2
2
2 0.0 1.0
3 0.0 1.0
Eigen — математическая библиотека
Перед тем, как приступить к написанию кода, я хотел бы рассказать о математической библиотеке — Eigen. Это зрелая, надежная и эффективная библиотека, которая обладает очень чистым и выразительным API. В ней есть множество compile-time оптимизаций, библиотека способна выполнять явную векторизацию и поддерживает SSE 2/3/4, ARM и NEON инструкции. Как по мне, эта библиотека замечательна хотя бы тем, что позволяет реализовывать сложные математические вычисления кратким и выразительным образом.
Я хотел бы сделать краткое описание части API Eigen, которое мы будем использовать далее. Те читатели, которые знакомы с этой библиотекой, могут пропустить этот раздел.
Есть два типа матриц: плотная и разреженные. Мы будем использовать оба типа. В случае с плотной матрицей, все элементы находятся в памяти, в порядке следования индексов, поддерживаются как column-major (дефолтный) так и raw-major размещение. Этот тип матриц хорош для относительно небольших матриц или матриц с небольшим количеством нулевых элементов. Разреженные матрицы хороши для хранения больших матриц с небольшим количеством ненулевых элементов. Мы будем использовать разреженную матрицу для глобальной матрицы жесткости.
Плотные матрицы
Для использования плотных матриц нам нужно будет включить заголовок <Eigen/Dense>. Есть два основных типа плотных матриц: с фиксированным и с динамическим размером. Матрица с фиксированным размером, это такая матрица, размер которой известен во время компиляции. В случае с матрицей динамического размера, ее размер может быть задан на этапе выполнения кода, более того, размер динамической матрицы можно даже изменять налету. Конечно, нужно отдавать предпочтение матрицам с фиксированным размером везде, где это возможно. Память под динамические матрицы выделяется в куче, также неизвестный размер матрицы ограничивает оптимизации, которые компилятор может сделать. Фиксированные матрицы могут быть выделены в стеке, компилятор может развернуть циклы и многое другое. Стоит отметить, что также возможен смешанный тип, когда у матрицы фиксируется количество строк, но количество столбцов динамично, или наоборот.
Матрицы фиксированного размера могут быть определены следующим образом:
Eigen::Matrix<float, 3, 3> m;Где m — float матрица c фиксированный размеров 3 × 3. Также можно использовать следующие предопределенные типы:
Eigen::Matrix2i
Eigen::Matrix3i
Eigen::Matrix4i
Eigen::Matrix2f
Eigen::Matrix3f
Eigen::Matrix4f
Eigen::Matrix2d
Eigen::Matrix3d
Eigen::Matrix4d
Есть немного больше предопределенных типов, эти являются основными. Цифра обозначает размерность квадратной матрицы и буква обозначает тип элемента матрицы: i — целое число, f — число с плавающей точкой одинарной точности, d — число с плавающей точкой двойной точности.
Для векторов нету отдельного типа, вектора такие-же матрицы. Вектор-столбец (иногда в литературе встречаются векторы-строки, приходится уточнять), можно объявить следующим образом:
Eigen::Matrix<float, 3, 1> v;Или можно использовать один из предопределенных типов (обозначения те же, что и для матриц):
Eigen::Vector2i
Eigen::Vector3i
Eigen::Vector4i
Eigen::Vector2f
Eigen::Vector3f
Eigen::Vector4f
Eigen::Vector2d
Eigen::Vector3d
Eigen::Vector4d
Для быстрого ознакомления, я написал следующий пример:
#include <iostream>
int main()
{
//Fixed size 3x3 matrix of floats
Eigen::Matrix3f A;
A << 1, 0, 1,
2, 5, 0,
1, 1, 2;
std::cout << "Matrix A:"
<< std::endl
<< A
<< std::endl;
//Access to matrix element [1, 1]:
std::cout << "A[1, 1]:"
<< std::endl
<< A(1, 1)
<< std::endl;
//Fixed size 3 vector of floats
Eigen::Vector3f B;
B << 1, 0, 1;
std::cout << "Vector B:"
<< std::endl
<< B
<< std::endl;
//Access to vector element [1]:
std::cout << "B[1]:"
<< std::endl
<< B(1)
<< std::endl;
//Multiplication of vector and matrix
Eigen::Vector3f C = A * B;
std::cout << "C = A * B:"
<< std::endl
<< C
<< std::endl;
//Dynamic size matrix of floats
Eigen::MatrixXf D;
D.resize(3, 3);
//Let matrix D be an identity matrix:
D.setIdentity();
std::cout << "Matrix D:"
<< std::endl
<< D
<< std::endl;
//Multiplication of matrix and matrix
Eigen::MatrixXf E = A * D;
std::cout << "E = A * D:"
<< std::endl
<< E
<< std::endl;
return 0;
}
Вывод:
Matrix A:
1 0 1
2 5 0
1 1 2
A[1, 1]:
5
Vector B:
1
0
1
B[1]:
0
C = A * B:
2
2
3
Matrix D:
1 0 0
0 1 0
0 0 1
E = A * D:
1 0 1
2 5 0
1 1 2
Для более подробной информации лучше обратиться к документации.
Разреженные матрицы
Разреженная матрица является немного более сложным, типом матрицы. Основная идея не хранить всю матрицу в памяти как есть, а хранить только ненулевые элементы. Довольно часто в практических задачах встречаются большие матрицы с малым количеством ненулевых элементов. При сборке глобальной матрицы жесткости в МКЭ модели, количество ненулевых элементов может быть меньше, чем 0,1% от общего числа элементов.
Для современных пакетов МКЭ не проблема решить задачу с сотней тысяч узлов, причем на вполне обычном современном PC. Если мы попытаемся выделить место для хранения глобальной матрицы жесткости, мы столкнемся со следующей проблемой:
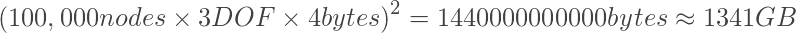
Размер памяти, необходимый для хранения матрицы огромный! Разреженная матрица потребуется в 10000 раз меньшее количество памяти.
Разреженные матрицы используют память более эффективно, так как хранят только ненулевые элементы. Разреженные матрицы могут быть представлены двумя способами: сжатым и несжатым. В несжатом виде легко добавить или удалить элемент из матрицы, но такой вид представления не является оптимальным с точки зрения использования памяти. Eigen, при работе с разреженной матрицей, использует своеобразное сжатое представление, несколько более оптимизированное для динамического добавления/удаления элементов. Eigen также умеет конвертировать такую матрицу в сжатый вид, более того он это делает прозрачно, делать это в явном виде не нужно. Большинство алгоритмов требуют сжатый вид матрицы, и применение любого из этих алгоритмов автоматически преобразует матрицу в сжатый вид. И наоборот, добавление/удаление элемента автоматически конвертирует матрицу в оптимизированное представление.
Как мы можем задать матрицу? Хороший способ это сделать — использовать так называемые Triplets. Это структура данных, причем это шаблонный класс, который представляет собой один элемент матрицы в комбинации с индексами, определяющими его положение в матрице. Мы можем задать разреженную матрицу непосредственно из вектора triplets.
Например, мы имеем следующую разреженную матрицу:
0 3 0 0 0
22 0 0 0 0
0 5 0 1 0
0 0 0 0 0
0 0 14 0 8
Первое, что мы должны сделать, это включить соответствующий заголовок библиотеки Eigen: <Eigen/Sparse>. Затем, мы объявляем пустую разреженную матрицу размерности 5х5. Далее, мы определяем вектор triplets и заполняем его значениями. Конструктор triplet'а принимает следующие аргументы: i-индекс, j-индекс, значение.
#include <Eigen/Sparse>
#include <iostream>
int main()
{
Eigen::SparseMatrix<int> A(5, 5);
std::vector< Eigen::Triplet<int> > triplets;
triplets.push_back(Eigen::Triplet<int>(0, 1, 3));
triplets.push_back(Eigen::Triplet<int>(1, 0, 22));
triplets.push_back(Eigen::Triplet<int>(2, 1, 5));
triplets.push_back(Eigen::Triplet<int>(2, 3, 1));
triplets.push_back(Eigen::Triplet<int>(4, 2, 14));
triplets.push_back(Eigen::Triplet<int>(4, 4, 8));
A.setFromTriplets(triplets.begin(), triplets.end());
A.insert(0, 0);
std::cout << A;
A.makeCompressed();
std::cout << std::endl << A;
}
Вывод будет следующим:
Nonzero entries:
(0,0) (22,1) (_,_) (3,0) (5,2) (_,_) (_,_) (14,4) (_,_) (_,_) (1,2) (_,_) (_,_) (8,4) (_,_) (_,_)
Outer pointers:
0 3 7 10 13 $
Inner non zeros:
2 2 1 1 1 $
0 3 0 0 0
22 0 0 0 0
0 5 0 1 0
0 0 0 0 0
0 0 14 0 8
Nonzero entries:
(0,0) (22,1) (3,0) (5,2) (14,4) (1,2) (8,4)
Outer pointers:
0 2 4 5 6 $
0 3 0 0 0
22 0 0 0 0
0 5 0 1 0
0 0 0 0 0
0 0 14 0 8
Структуры данных
Для хранения данных, которые мы собираемся читать из входного файла, а также промежуточных данных, мы должны объявить свои структуры. Простейшая структура данных описывающая конечный элемент показана ниже. Она состоит из массива трех элементов, которые хранят индексы узлов образующих конечный элемент, а также матрицы В. Данная матрица называемый градиентной матрицей и мы вернемся к ней позже. О методе CalculateStiffnessMatrix также будет рассказано далее.
struct Element
{
void CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets);
Eigen::Matrix<float, 3, 6> B;
int nodesIds[3];
};
Еще одна простая структура которая нам понадобится — это структура для описания закреплений. Это простая структура состоящая из перечисляемого типа, который определяет тип ограничения, и индекса узла на который накладывается ограничение.
struct Constraint
{
enum Type
{
UX = 1 << 0,
UY = 1 << 1,
UXY = UX | UY
};
int node;
Type type;
};
Чтобы не усложнять, давайте определим некоторые глобальные переменные. Создавать какие-либо глобальные объекты — это всегда плохая идея, но для этого примера вполне допустимо. Нам понадобятся следующие глобальные переменные:
- Количество узлов
- Вектор с х-координатой узлов
- Вектор с y-координатой узлов
- Вектор элементов
- Вектор закреплений
- Вектор нагрузок
В коде, мы определим их следующим образом:
int nodesCount;
int noadsCount;
Eigen::VectorXf nodesX;
Eigen::VectorXf nodesY;
Eigen::VectorXf loads;
std::vector< Element > elements;
std::vector< Constraint > constraints;
Чтение входного файла
Перед чем как что-то читать, мы должны знать откуда читать и куда писать вывод. В начале main функции проверим количество входных аргументов, обращаю внимание, что первый аргумент всегда путь к исполняемому файлу. Таким образом, у нас должно быть три аргумента, пусть второй будет путь к входному файлу, а третий — путь к файлу с выводом. Для работы с вводом/выводом, для конкретного случая удобнее всего использовать файловые потоки из стандартной библиотеки.
Первое, что мы делаем — создаем потоки для ввода/вывода:
int main(int argc, char *argv[])
{
if ( argc != 3 )
{
std::cout << "usage: " << argv[0] << " <input file> <output file>\n";
return 1;
}
std::ifstream infile(argv[1]);
std::ofstream outfile(argv[2]);
В первой строке входного файла находятся свойства материала, прочитаем их:
float poissonRatio, youngModulus;
infile >> poissonRatio >> youngModulus;
Этого достаточно, чтобы построить матрицу упругости изотропного материала для плоско-напряженного состояния, которая определена следующим образом:

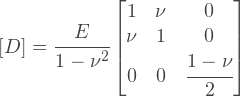
Откуда взялись эти выражения? Они легко получаются из закона Гука в общем виде, действительно, мы можем найти выражение для матрицы D из следующих соотношений:
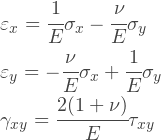
Стоит отметить, что плоско-напряженное состояние означает, что σZ равно нулю, но не εZ. Плоско-напряженная модель хорошо подходит для решения ряда инженерных задач, где рассматриваются плоские структуры и все силы действуют в плоскости. Во времена, когда расчеты объемных задач были слишком дорогими, множество задач удавалось свести к плоским, жертвуя при этом точностью.
При плоско-напряженном состоянии, ничто не мешает телу деформироваться в направлении нормали к его плоскости, поэтому деформация εZ в общем случае не равна нулю. Она не появляется в уравнениях выше, но может быть легко получена из следующего соотношения, учитывая что напряжение σZ равно нулю:
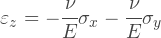
У нас есть все исходные данные чтобы задать матрицу упругости, давайте сделаем это:
Eigen::Matrix3f D;
D <<
1.0f, poissonRatio, 0.0f,
poissonRatio, 1.0, 0.0f,
0.0f, 0.0f, (1.0f - poissonRatio) / 2.0f;
D *= youngModulus / (1.0f - pow(poissonRatio, 2.0f));
Далее, мы читаем список с координатами узлов. Сначала читаем количество узлов, затем задаем размер динамических векторов х и у. Далее, мы просто читать координаты узлов в цикле, строка за строкой.
infile >> nodesCount;
nodesX.resize(nodesCount);
nodesY.resize(nodesCount);
for (int i = 0; i < nodesCount; ++i)
{
infile >> nodesX[i] >> nodesY[i];
}
Затем, мы читаем список элементов. Все то-же самое, читаем количество элементов, а затем индексы узлов для каждого элемента:
int elementCount;
infile >> elementCount;
for (int i = 0; i < elementCount; ++i)
{
Element element;
infile >> element.nodesIds[0] >> element.nodesIds[1] >> element.nodesIds[2];
elements.push_back(element);
}
Далее, читаем список закреплений. Все то же самое:
int constraintCount;
infile >> constraintCount;
for (int i = 0; i < constraintCount; ++i)
{
Constraint constraint;
int type;
infile >> constraint.node >> type;
constraint.type = static_cast<Constraint::Type>(type);
constraints.push_back(constraint);
}
Вы могли заметить static_cast, он нужен чтобы преобразовать int тип, в объявленный нами ранее перечисляемый тип для закреплений.
Наконец, нужно прочитать список нагрузок. Есть одна особенность связанная с нагрузкой, из-за которой мы будем представлять действующие нагрузки в виде вектора размерности двойного количества узлов. Причина, почему мы делаем так, будет объяснена чуть позже. Рисунок ниже, иллюстрирует этот вектор нагрузки:
Таким образом, для каждого узла, у нас есть два элемента в векторе нагрузки, которые представляют х и у компоненты усилия. Таким образом, х-компонента усилия в определенном узле будет храниться в элементе с индексом id = 2 * node_id + 0, а у-составляющая усилия для этого узла будет храниться в элементе с индексом id = 2 * node_id + 1.
Сначала зададим размер вектора приложенных усилий вдвое больший, чем количество узлов, затем обнулим вектор. Читаем количество внешних сил и читаем их значения строка за строкой:
int loadsCount;
loads.resize(2 * nodesCount);
loads.setZero();
infile >> loadsCount;
for (int i = 0; i < loadsCount; ++i)
{
int node;
float x, y;
infile >> node >> x >> y;
loads[2 * node + 0] = x;
loads[2 * node + 1] = y;
}
Расчет глобальной матрицы жесткости
Мы рассматриваем геометрически линейную систему с бесконечно малыми перемещениями. Более того, мы предполагаем, что деформирование происходит упруго, т.е. деформации являются линейной функцией напряжений (закон Гука). Из основ строительной механики можно показать, что перемещение каждого узла является линейной функцией приложенных сил. Таким образом, мы можем говорить, что у нас есть следующая система линейных уравнений:

Где: К — матрица жесткости; δ — вектор перемещений; R — вектор нагрузок, то есть вектор внешних сил. Эту систему линейных уравнений часто называют ансамблем, так как она представляет суперпозицию матриц жесткости каждого элемента, как это будет показано ниже.
Вектор перемещений, для двумерных проблем может быть задан следующим образом:
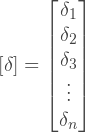
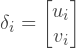
Где: ui и vi — u-компонента и v-компонента перемещения i-го узла.
Вектор внешних сил:
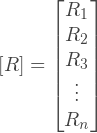
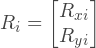
Где: Rxi и Ryi — х-компонента и y-компонента внешнего усилия приложенного к i-му узлу.
Как мы видим, каждый элемент вектора перемещения и вектора нагрузок является двумерным вектором. Вместо этого, мы можем определить эти векторы следующим образом:

То есть фактически то же самое, но это упрощает представление этих векторов в коде. Это объяснение, почему мы ранее задали вектор нагрузки таким своеобразным способом.
Как построить матрицу жесткости? Суть глобальной матрицы жесткости есть суперпозиция матриц жесткости каждого элемента. Если мы рассмотрим один элемент отдельно от остальных, то мы можем определить такую-же матрицу жесткости, но только для данного элемента. Эта матрица определяет соотношения между перемещениями узлов и узловыми силами. Например для 3-узлового элемента:

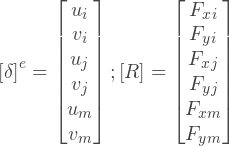
Где: [k]е — матрица жесткости e-го элемента; [δ]е — вектор перемещений узлов е-го элемента; [F]е — вектор узловых сил е-го элемента; i, j, m — индексы узлов элемента.
Что произойдет, если один узел будет разделен между двумя элементами? Прежде всего, поскольку это все тот-же узел, перемещение соответственно не будет зависеть от того в составе какого элемента мы рассматриваем этот узел. Вторым важным следствием является то, что если суммировать все узловые силы от каждого элемента в этом узле, то результат будет равен внешней силе, иными словами — нагрузке.
Сумма всех узловых сил в каждом узле равна сумме внешних сил в этом узле, это следует из принципа равновесия. Несмотря на то, что данное утверждение может показаться вполне логичным и справедливым, на самом деле все немного сложнее. Такая формулировка не является точной, потому что узловые силы не являются силами в общем смысле этого слова, и выполнение условий равновесия для них вовсе не очевидное условие. Несмотря на то, что утверждение все же верное, оно использует механический принцип, чем ограничевает применение метода. Существует более строгое, математическое обоснование МКЭ с позиций минимизации потенциальной энергии, что позволяет распространить метод на более широкий спектр задач.
На мой взгляд, об узловых силах лучше думать как о неких обобщенных силах, в представлении Лагранжевой механики. Дело в том, что перемещение узла, на самом деле является обобщенным перемещением, так как оно однозначно характеризует поле перемещений внутри элемента. Каждую компоненту перемещения узла можно трактовать как обобщенную координату, следовательно и силы, действуют не в точке узла, а по границе элемента (или по объему для объемных сил), причем действуют именно на том перемещении, которое характеризует данный узел.
Если просуммировать все уравнения для каждого узла, меж-элементные узловые силы уйдут. С правой стороны уравнения останутся только внешние силы — нагрузки. Таким образом, учитывая этот факт, мы можем написать:

Рисунок ниже иллюстрирует вышеприведенное выражение:

Для построения глобальной матрицы жесткости, нам понадобится вектор triplets. В цикле, мы пройдемся по каждому элементу и заполним этот вектор значениями матриц жесткости полученными от каждого элемента:
std::vector<Eigen::Triplet<float> > triplets;
for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it)
{
it->CalculateStiffnessMatrix(D, triplets);
}
Где std::vector<Eigen::Triplet<float> > — вектор triplets; CalculateStiffnessMatrix — метод класса элемента, который заполняет вектор triplets.
Как уже упоминалось ранее, мы можем построить глобальную разреженную матрицу прямо из вектора triplets:
Eigen::SparseMatrix<float> globalK(2 * nodesCount, 2 * nodesCount);
globalK.setFromTriplets(triplets.begin(), triplets.end());
Расчет матрицы жесткости отдельных элементов
Мы выяснили, как собрать глобальную матрицу жесткости (ансамбль) из матриц элементов, Осталось выяснить как получить матрицу жесткости элемента.
Функции формы
Давайте начнем с интерполяции перемещений внутри элемента основываясь на перемещениях его узлов. Если перемещения узлов заданы, то перемещение в любой точке элемента можно представить как:
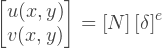
Где [N] представляет собой матрицу функций координат (х, у). Эти функции называются функциями формы. Каждую компоненту перемещения, u и v можно интерполировать независимо, тогда уравнение выше, можно переписать в следующем виде:
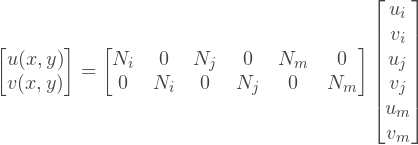
Или можно записать в раздельной форме:


Как получить инерполирующую функцию? Для простоты, давайте рассмотрим скалярное поле. В случае трех-узлового, линейного элемента, функция интерполяции является линейной. Интерполяционное выражение мы будем искать в следующем виде:

Если значения f в узлах известны, то мы можем задать систему из трех уравнений:
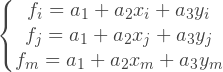
Или в матричной форме:

Из этой системы уравнений, мы можем найти неизвестный вектор коэффициентов для интерполирующего выражения:
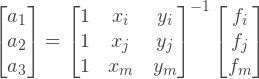
Введем обозначение
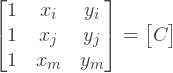
Наконец, получим интерполяционное выражение:
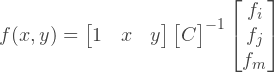
Возвращаясь к перемещениям, мы можем сказать, что:

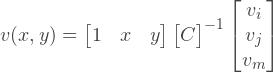
Тогда, функции формы будут иметь вид:

Деформации и градиентная матрица
Зная поле перемещений, мы можем найти поле деформаций, по соотношениям из теории упругости:
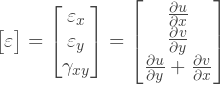
Теперь мы можем заменить u и v, на функции формы:
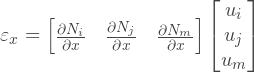

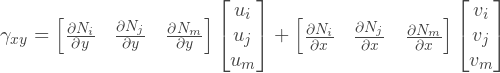
Или мы можем написать то же самое в комбинированной форме:

Матрица с правой стороны, обычно обозначается как матрица В, так называемая градиентная матрица.

Чтобы найти матрицу В, мы должны найти все частные производные функций формы:


В случае с линейным элементом, мы видим, что частные производные функций формы на самом деле являются константами, что сэкономит нам множество усилий, как это будет показано далее. Умножив вектор-строку с константами на обратную матрицу C получим:


Теперь мы можем рассчитать B матрицу. Чтобы построить матрицу C, сначала зададим векторы координат узлов:
Eigen::Vector3f x, y;
x << nodesX[nodesIds[0]], nodesX[nodesIds[1]], nodesX[nodesIds[2]];
y << nodesY[nodesIds[0]], nodesY[nodesIds[1]], nodesY[nodesIds[2]];
Затем, мы можем построить матрицу С из трех строк:
Eigen::Matrix3f C;
C << Eigen::Vector3f(1.0f, 1.0f, 1.0f), x, y;
Затем мы вычисляем обратную матрицу С и собираем матрицу B:
Eigen::Matrix3f IC = C.inverse();
for (int i = 0; i < 3; i++)
{
B(0, 2 * i + 0) = IC(1, i);
B(0, 2 * i + 1) = 0.0f;
B(1, 2 * i + 0) = 0.0f;
B(1, 2 * i + 1) = IC(2, i);
B(2, 2 * i + 0) = IC(2, i);
B(2, 2 * i + 1) = IC(1, i);
}
Переход к напряжениям
Как мы уже упоминали ранее, соотношение между напряжением и деформацией можно записать с помощью матрицы упругости D:

Таким образом, подставляя выражение выше в соотношение для деформаций, получим:

Здесь мы видим, что напряжения, как и деформации являются константами внутри элемента. Это особенность линейных элементов. Однако, для элементов более высоких порядков, неразрывность напряжений также не выполняется. При увеличении числа элементов, эти разрывы должны уменьшаться что является критерием сходимости. На практике, обычно вычисляют среднее значение деформаций для каждого узла, однако в нашем случае мы оставим все как есть.
Принцип виртуальной работы
Для того, чтобы перейти к матрице жесткости, мы должны обратиться к виртуальной работе. Скажем, у нас есть некие виртуальные перемещения в узлах элемента: d[δ]e
Виртуальные перемещения должны пониматься как любые бесконечно малые перемещения, которые могут произойти. Мы знаем, что в случае с нашей задачей, существует только одно решение и только один набор перемещений будет иметь место, но здесь мы рассматриваем все немного под другим углом. Другими словами, мы берем все бесконечно малые перемещения которые разрешены кинематически, а затем находим те единственные, которые удовлетворяют физический закон.
Для этих виртуальных перемещений, виртуальная работа узловых сил будет:

Виртуальная работа внутренних напряжений в единице объема для тех-же виртуальный перемещений:

Или:
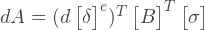
Подставляя уравнение для напряжений, мы получим:

Из закона сохранения энергии, виртуальная работа внешних сил должна быть равна сумме работы внутренних напряжений по объему элемента:
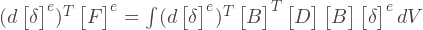
Так, как это соотношение должно быть справедливо для любого виртуального перемещения, мы можем разделить обе части уравнения на виртуальное перемещение:

Узловые перемещения можно вынести за интеграл, так как они постоянны внутри элемента. Теперь мы видим, что интеграл является коэффициентом пропорциональности между узловыми перемещениями и узловыми силами, это означает, что интеграл представляет собой матрицу жесткости:
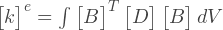
Для линейного элемента, как мы получили ранее, матрица В является константой. Если свойства материала также постоянны, то интеграл становится тривиальным:

Где A — площадь элемента, t — толщина элемента. Из свойств треугольника, его площадь может быть получена как половина детерминанта матрицы С:

В конце концов, мы можем записать следующий код для вычисления матрицы жесткости:
Eigen::Matrix<float, 6, 6> K = B.transpose() * D * B * C.determinant() / 2.0f;Здесь я опустил толщину, будем считать что она у нас единична. Обычно, на практике используют следующую систему единиц: МПа, мм2. В этом случае, если мы задаем модуль упругости в мегапаскалях, а размеры в миллиметрах, то толщина будет один миллиметр. Если нужна другая толщина, то ее легко можно внести в модуль упругости. В более общем случае, лучше всего задавать толщину поэлементно или даже для каждого узла.
Метод CalculateStiffnessMatrix целиком:
void Element::CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets)
{
Eigen::Vector3f x, y;
x << nodesX[nodesIds[0]], nodesX[nodesIds[1]], nodesX[nodesIds[2]];
y << nodesY[nodesIds[0]], nodesY[nodesIds[1]], nodesY[nodesIds[2]];
Eigen::Matrix3f C;
C << Eigen::Vector3f(1.0f, 1.0f, 1.0f), x, y;
Eigen::Matrix3f IC = C.inverse();
for (int i = 0; i < 3; i++)
{
B(0, 2 * i + 0) = IC(1, i);
B(0, 2 * i + 1) = 0.0f;
B(1, 2 * i + 0) = 0.0f;
B(1, 2 * i + 1) = IC(2, i);
B(2, 2 * i + 0) = IC(2, i);
B(2, 2 * i + 1) = IC(1, i);
}
Eigen::Matrix<float, 6, 6> K = B.transpose() * D * B * C.determinant() / 2.0f;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
Eigen::Triplet<float> trplt11(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 0, K(2 * i + 0, 2 * j + 0));
Eigen::Triplet<float> trplt12(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 1, K(2 * i + 0, 2 * j + 1));
Eigen::Triplet<float> trplt21(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 0, K(2 * i + 1, 2 * j + 0));
Eigen::Triplet<float> trplt22(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 1, K(2 * i + 1, 2 * j + 1));
triplets.push_back(trplt11);
triplets.push_back(trplt12);
triplets.push_back(trplt21);
triplets.push_back(trplt22);
}
}
}В конце метода, после вычисления матрицы жесткости, заполняется вектор Triplets. Каждый Triplet создается используя массив индексов узлов элемента, чтобы определить его положение в глобальной матрице жесткости. На всякий случай, подчеркну, что у нас есть два набора индексов, один локальный — для матрицы элемента, другой глобальный — для ансамбля.
Задание закреплений
Полученная система линейных уравнений не может быть решена до тех пор, пока мы не зададим закрепления. Чисто с механической точки зрения, незакрепленная система может совершать любые большие перемещения, а под действием внешних сил и вовсе перейдет в движение. Математически, это приведет к тому, что полученная СЛАУ не является линейно независимой, а следовательно не имеет единственного решения.
Перемещения некоторых узлов должны быть установлены в ноль или в некоторую заранее заданную величину. В простейшем случае, давайте рассмотрим только закрепления узлов, без начальных смещений. На самом деле это означает, что мы удаляем некоторые уравнения из системы. Но изменение количества уравнения системы на лету, не тривиальная задача. Вместо этого можно воспользоваться следующим трюком.
Скажем, мы имеем следующую систему уравнений:
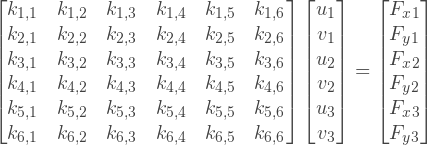
Чтобы закрепить узел, соответствующий элемент матрицы должен быть установлен в 1, и все элементы в строке и столбце содержащие этот элемент должны быть установлены в ноль. Так же не должно быть никаких внешних сил, действующих на закрепленный узел в направлении в котором действует ограничение. Уравнение с этим узлом, явно даст нулевое смещение для этого узла, а нули в соответствующем столбце исключат это смещение из других уравнений. Скажем, мы хотим закрепить нулевой узел в направлении оси х, и закрепить первый узел в направлении оси у:

Чтобы выполнить эту операцию, сначала определим индексы уравнений, которые мы собираемся исключать из СЛАУ. Чтобы это сделать, мы в цикле пройдемся по списку закреплений и соберем вектор индексов. Затем, перебирая все ненулевые элементы матрицы жесткости вызываем функцию SetConstraints. Ниже приведена функция ApplyConstraints:
void ApplyConstraints(Eigen::SparseMatrix<float>& K, const std::vector<Constraint>& constraints)
{
std::vector<int> indicesToConstraint;
for (std::vector<Constraint>::const_iterator it = constraints.begin(); it != constraints.end(); ++it)
{
if (it->type & Constraint::UX)
{
indicesToConstraint.push_back(2 * it->node + 0);
}
if (it->type & Constraint::UY)
{
indicesToConstraint.push_back(2 * it->node + 1);
}
}
for (int k = 0; k < K.outerSize(); ++k)
{
for (Eigen::SparseMatrix<float>::InnerIterator it(K, k); it; ++it)
{
for (std::vector<int>::iterator idit = indicesToConstraint.begin(); idit != indicesToConstraint.end(); ++idit)
{
SetConstraints(it, *idit);
}
}
}
}
Функция SetConstraints проверяет, является ли элемент матрицы жесткости частью исключенного уравнения, и если это так, то он устанавливает его равным нулю или единице в зависимости от того, находится ли элемент на диагонали или нет:
void SetConstraints(Eigen::SparseMatrix<float>::InnerIterator& it, int index)
{
if (it.row() == index || it.col() == index)
{
it.valueRef() = it.row() == it.col() ? 1.0f : 0.0f;
}
}
Далее, мы просто вызываем ApplyConstraints и передаем ей в качестве аргументов глобальную матрицу жесткости и вектор закреплений:
ApplyConstraints(globalK, constraints);Решение СЛАУ и вывод результата
Библиотека Eigen имеет в наличии различные решатели разреженных линейных уравнений, мы будем использовать SimplicialLDLT, который является быстрым прямым решателем. Для демонстрационных целей, мы будем выводить исходную матрицу жесткости и вектор нагрузки, а затем выводить результат решения — вектор перемещений.
std::cout << "Global stiffness matrix:\n";
std::cout << static_cast<const Eigen::SparseMatrixBase<Eigen::SparseMatrix<float> >& > (globalK) << std::endl;
std::cout << "Loads vector:" << std::endl << loads << std::endl << std::endl;
Eigen::SimplicialLDLT<Eigen::SparseMatrix<float> > solver(globalK);
Eigen::VectorXf displacements = solver.solve(loads);
std::cout << "Displacements vector:" << std::endl << displacements << std::endl;
outfile << displacements << std::endl;
Разумеется, вывод матрицы имеет смысл только для нашего тестового примера, содержащего всего два элемента.
Анализ полученного результата
Как мы уже видели раньше, мы можем перейти от перемещений к деформациям а далее к напряжениям:

Однако, мы получаем вектор напряжений, который в теории упругости вообще говоря представляет собой симметричный тензор второго ранга:
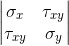
Как известно, непосредственно элементы тензора зависят от системы координат, однако само физическое состояние конечно не зависит. Поэтому для анализа лучше перейти как какой либо инвариантной величине, лучше всего к скалярной. Таким инвариантом являются напряжения по Мизесу:
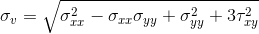
Эта скалярная величина, позволяет оценить напряжения при сложно-напряженном состоянии, так как если бы мы имели дело с одноосным напряженным состоянием. Данный критерий не идеален, но в большинстве случаем, для статического анализа дает более менее правдоподобную картину, поэтому он чаще всего используется на практике.
Теперь мы в цикле пройдемся по всем элементам, и расчитаем напряжения по Мизесу для каждого элемента:
std::cout << "Stresses:" << std::endl;
for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it)
{
Eigen::Matrix<float, 6, 1> delta;
delta << displacements.segment<2>(2 * it->nodesIds[0]),
displacements.segment<2>(2 * it->nodesIds[1]),
displacements.segment<2>(2 * it->nodesIds[2]);
Eigen::Vector3f sigma = D * it->B * delta;
float sigma_mises = sqrt(sigma[0] * sigma[0] - sigma[0] * sigma[1] + sigma[1] * sigma[1] + 3.0f * sigma[2] * sigma[2]);
std::cout << sigma_mises << std::endl;
outfile << sigma_mises << std::endl;
}
На этом написание нашего простейшего МКЭ расчетчика можно считать законченным. Посмотрим, какой вывод мы получим для нашей тестовой задачи:
Global stiffness matrix:
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1483.52 0 0 714.286 -384.615 -384.615
0 0 0 1 0 0 0 0
0 0 0 0 1483.52 0 -1098.9 -329.67
0 0 714.286 0 0 1483.52 -384.615 -384.615
0 0 -384.615 0 -1098.9 -384.615 1483.52 714.286
0 0 -384.615 0 -329.67 -384.615 714.286 1483.52
Loads vector:
0
0
0
0
0
1
0
1
Deformations vector:
0
0
-0.0003
0
-5.27106e-011
0.001
-0.0003
0.001
Stresses:
2
2
Мы видим, что закрепления мы задали верно, деформации закрепленных узлов в соответствующих направлениях равны нулю. Деформации верхних узлов направлены вверх, в соответствии с растягивающим усилием. Деформации в x-направлении, для правой пары узлов составляют величину 0.0003, что есть 0.3 часть от деформаций верхних узлов в y-направлении, что является эффектом Пуассона. Результат расчета полностью согласуется с ожиданиями, поэтому можно переходить к задачам поинтереснее.
Весь код целиком
#include <Eigen/Dense>
#include <Eigen/Sparse>
#include <string>
#include <vector>
#include <iostream>
#include <fstream>
struct Element
{
void CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets);
Eigen::Matrix<float, 3, 6> B;
int nodesIds[3];
};
struct Constraint
{
enum Type
{
UX = 1 << 0,
UY = 1 << 1,
UXY = UX | UY
};
int node;
Type type;
};
int nodesCount;
Eigen::VectorXf nodesX;
Eigen::VectorXf nodesY;
Eigen::VectorXf loads;
std::vector< Element > elements;
std::vector< Constraint > constraints;
void Element::CalculateStiffnessMatrix(const Eigen::Matrix3f& D, std::vector<Eigen::Triplet<float> >& triplets)
{
Eigen::Vector3f x, y;
x << nodesX[nodesIds[0]], nodesX[nodesIds[1]], nodesX[nodesIds[2]];
y << nodesY[nodesIds[0]], nodesY[nodesIds[1]], nodesY[nodesIds[2]];
Eigen::Matrix3f C;
C << Eigen::Vector3f(1.0f, 1.0f, 1.0f), x, y;
Eigen::Matrix3f IC = C.inverse();
for (int i = 0; i < 3; i++)
{
B(0, 2 * i + 0) = IC(1, i);
B(0, 2 * i + 1) = 0.0f;
B(1, 2 * i + 0) = 0.0f;
B(1, 2 * i + 1) = IC(2, i);
B(2, 2 * i + 0) = IC(2, i);
B(2, 2 * i + 1) = IC(1, i);
}
Eigen::Matrix<float, 6, 6> K = B.transpose() * D * B * C.determinant() / 2.0f;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
Eigen::Triplet<float> trplt11(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 0, K(2 * i + 0, 2 * j + 0));
Eigen::Triplet<float> trplt12(2 * nodesIds[i] + 0, 2 * nodesIds[j] + 1, K(2 * i + 0, 2 * j + 1));
Eigen::Triplet<float> trplt21(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 0, K(2 * i + 1, 2 * j + 0));
Eigen::Triplet<float> trplt22(2 * nodesIds[i] + 1, 2 * nodesIds[j] + 1, K(2 * i + 1, 2 * j + 1));
triplets.push_back(trplt11);
triplets.push_back(trplt12);
triplets.push_back(trplt21);
triplets.push_back(trplt22);
}
}
}
void SetConstraints(Eigen::SparseMatrix<float>::InnerIterator& it, int index)
{
if (it.row() == index || it.col() == index)
{
it.valueRef() = it.row() == it.col() ? 1.0f : 0.0f;
}
}
void ApplyConstraints(Eigen::SparseMatrix<float>& K, const std::vector<Constraint>& constraints)
{
std::vector<int> indicesToConstraint;
for (std::vector<Constraint>::const_iterator it = constraints.begin(); it != constraints.end(); ++it)
{
if (it->type & Constraint::UX)
{
indicesToConstraint.push_back(2 * it->node + 0);
}
if (it->type & Constraint::UY)
{
indicesToConstraint.push_back(2 * it->node + 1);
}
}
for (int k = 0; k < K.outerSize(); ++k)
{
for (Eigen::SparseMatrix<float>::InnerIterator it(K, k); it; ++it)
{
for (std::vector<int>::iterator idit = indicesToConstraint.begin(); idit != indicesToConstraint.end(); ++idit)
{
SetConstraints(it, *idit);
}
}
}
}
int main(int argc, char *argv[])
{
if ( argc != 3 )
{
std::cout<<"usage: "<< argv[0] <<" <input file> <output file>\n";
return 1;
}
std::ifstream infile(argv[1]);
std::ofstream outfile(argv[2]);
float poissonRatio, youngModulus;
infile >> poissonRatio >> youngModulus;
Eigen::Matrix3f D;
D <<
1.0f, poissonRatio, 0.0f,
poissonRatio, 1.0, 0.0f,
0.0f, 0.0f, (1.0f - poissonRatio) / 2.0f;
D *= youngModulus / (1.0f - pow(poissonRatio, 2.0f));
infile >> nodesCount;
nodesX.resize(nodesCount);
nodesY.resize(nodesCount);
for (int i = 0; i < nodesCount; ++i)
{
infile >> nodesX[i] >> nodesY[i];
}
int elementCount;
infile >> elementCount;
for (int i = 0; i < elementCount; ++i)
{
Element element;
infile >> element.nodesIds[0] >> element.nodesIds[1] >> element.nodesIds[2];
elements.push_back(element);
}
int constraintCount;
infile >> constraintCount;
for (int i = 0; i < constraintCount; ++i)
{
Constraint constraint;
int type;
infile >> constraint.node >> type;
constraint.type = static_cast<Constraint::Type>(type);
constraints.push_back(constraint);
}
loads.resize(2 * nodesCount);
loads.setZero();
infile >> loadsCount;
int loadsCount;
for (int i = 0; i < loadsCount; ++i)
{
int node;
float x, y;
infile >> node >> x >> y;
loads[2 * node + 0] = x;
loads[2 * node + 1] = y;
}
std::vector<Eigen::Triplet<float> > triplets;
for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it)
{
it->CalculateStiffnessMatrix(D, triplets);
}
Eigen::SparseMatrix<float> globalK(2 * nodesCount, 2 * nodesCount);
globalK.setFromTriplets(triplets.begin(), triplets.end());
ApplyConstraints(globalK, constraints);
Eigen::SimplicialLDLT<Eigen::SparseMatrix<float> > solver(globalK);
Eigen::VectorXf displacements = solver.solve(loads);
outfile << displacements << std::endl;
for (std::vector<Element>::iterator it = elements.begin(); it != elements.end(); ++it)
{
Eigen::Matrix<float, 6, 1> delta;
delta << displacements.segment<2>(2 * it->nodesIds[0]),
displacements.segment<2>(2 * it->nodesIds[1]),
displacements.segment<2>(2 * it->nodesIds[2]);
Eigen::Vector3f sigma = D * it->B * delta;
float sigma_mises = sqrt(sigma[0] * sigma[0] - sigma[0] * sigma[1] + sigma[1] * sigma[1] + 3.0f * sigma[2] * sigma[2]);
outfile << sigma_mises << std::endl;
}
return 0;
}Запустим утилиту cloc:
-------------------------------------------------------------------------------
Language files blank comment code
-------------------------------------------------------------------------------
C++ 1 37 0 171
-------------------------------------------------------------------------------Как видим, всего ничего — 171 строчка кода.
Немного картинок
Для визуализации результатов расчета, был написан скрипт на python, который рисует недеформированный и деформированный меш с полем напряжений. К сожалению, я не знаю как сделать градиентную заливку с помощью PIL, поэтому напряжения внутри элемента отображаются как сплошная константная заливка. Abaqus умеет делать визуализацию и в таком виде, что хоть и выглядит менее красиво, за то ближе к правде.
Тестовая задача:

Для получения сеток посложнее, была использована бесплатная студенческая версия Abaqus. Для конвертации входного файла Abaqus'а был написан еще один скрипт. Правда задавать закрепления и внешние нагрузки все равно придется вручную.
Здесь мы видим полосу с отверстием, низ которой закреплен, а к верхней кромке приложено растягивающее усилие:

Абстрактный элемент конструкции, просто для красоты. Низ конструкции закреплен, а на верхнюю выступающую часть приложена сконцентрированая сила, которую я нарисовал уже поверх картинки:
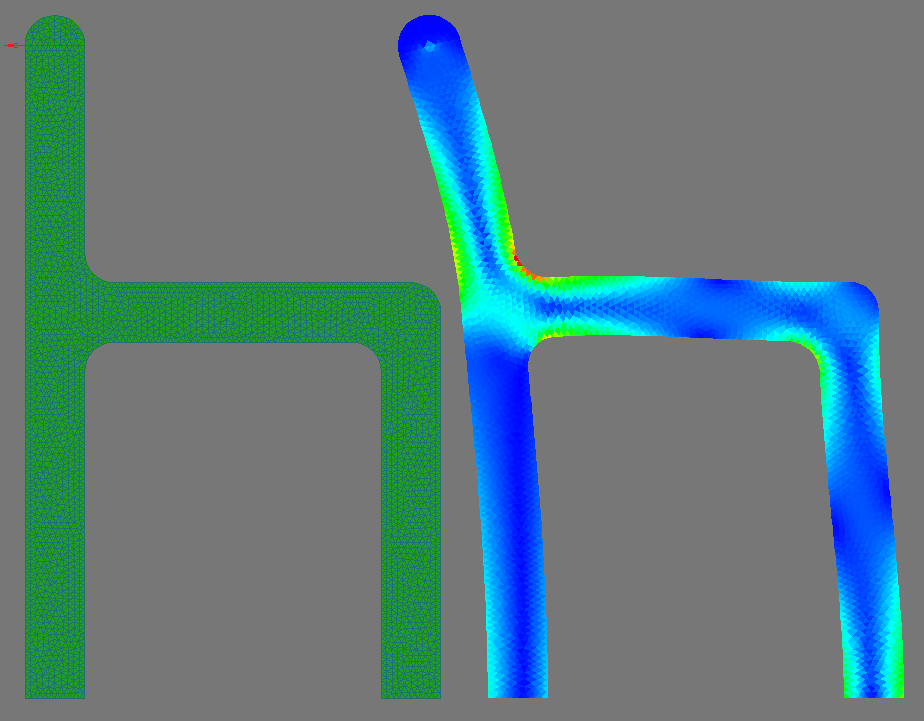
Еще один пример с полосой с отверстием, на этот раз рассмотрена только четверть конструкции в силу симметрии. Левая граница закреплена по оси x, нижняя — по оси y. Максимальное полученное напряжение: 3.05152. Данная величина, несмотря на грубость сетки (а может и благодаря ей), достаточно близка к теоретическому значению — 3.
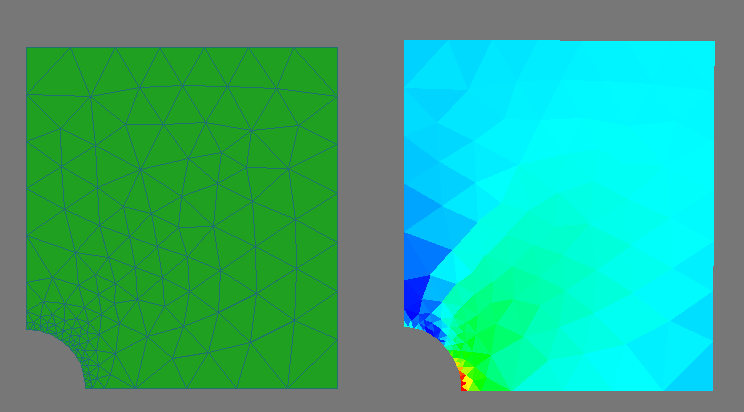
Та-же задача, но решенная в Abaqus. Как видим максимальное напряжение — 3.052, что полностью совпадает с нашим результатом. Такое точное совпадение в принципе не мудрено, так как практически, для треугольного элемента трудно сделать что-то каким-то своим способом, так чтобы результат отличался. Для элементов более высокого порядка у меня к сожалению такого 100%-го совпадения не получилось, что может быть объяснено разной реализацией численного интегрирования.
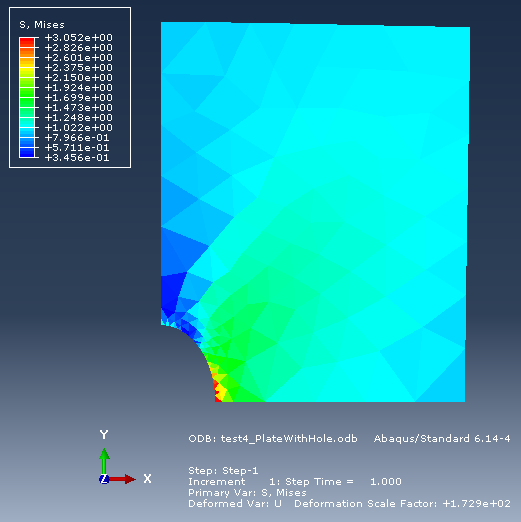
Весь исходный код, включая примеры доступен на github'е.
Что осталось за кадром
Честно говоря, за кадром осталось достаточно много. Но статья оказалась и так раздута, поэтому думаю на этом можно остановиться.
Не вошло (а хотелось):
- Задание внешних нагрузок. Как было сказано, в исходном файле мы задаем узловые силы. Но к ним еще нужно перейти от внешних нагрузок. В случае сконцентрированной силы тут все тривиально, но в случае приложения давления (как в 2-м и 4-м примере), здесь все не так просто. В случае элементов более высоких порядков, результат даже немного неожиданный (с точки зрения инженерной интуиции).
- Не коснулся я важных свойств функций формы.
- Хотелось поговорить о элементах более высоких порядков, на примере изопараметрических элементов.
- Хотелось так-же показать, как выполнить численное интегрирование для элементов более высоких порядков. Это отдельная, весьма любопытная тема.
- С минимальными изменениями в коде, можно выполнить динамический анализ, когда учитываются силы инерции и система приходит в движение.
- Можно было, наряду с рассмотрением равновесия узловых сил, привести более общее обоснование метода, исключающее эти узловые силы вообще.
Я думаю, что многие могут справедливо заметить, что в современных математических пакетах, таких как MATLAB есть инструменты для работы с МКЭ, и в принципе нет необходимости что либо писать на С++. Однако, здесь я все же хотел показать минимальную реализацию, с минимумом зависимостей, т.е. без использования сторонних инструментов. За исключением математической библиотеки конечно, но думаю, что все использованные функции для читателей должны быть предельно прозрачны.
P.S. Статья большая, уверен опечаток много, пожалуйста в личку.