На прошлой неделе Phys.org разразился новостью: стартап LightOn предложил альтернативу центральным процессорам (CPU) и графическим процессорам (GPU) для решения задач анализа больших данных. Авторский коллектив базируется в университете Пьера и Марии Кюри, Сорбонне и всех прочих правильных местах во Франции. Решение основано на оптической аналоговой обработке данных «со скоростью света». Звучит интересно. Поскольку в пресс-релизе не было никаких научно-технических подробностей, пришлось поискать информацию в патентных базах данных и на сайтах университетов. Результаты расследования под катом.
Решение LightOn основано на сравнительно новом классе алгоритмов, основанном на случайных проекциях данных. Перемешивание данных воспроизводимым и контролируемым образом позволяет извлекать полезную информацию, например для решения задач классификации или compressive sensing (русского термина не знаю). При работе с большими объёмами данных лимитирующим фактором является именно вычисление случайных проекций. LightOn разработал оптическую схему расчёта случайных проекций и сейчас получает финансирование на разработку сопроцессора, который способен при минимальных затратах энергии выполнять всю тяжёлую работу по извлечению существенных признаков из сырых данных в потоковом режиме.
Это позволит, например, заменить графические процессоры при обработке видео- и аудиоданных в мобильных устройствах. Оптический сопроцессор потребляет единицы Ватт, и поэтому может работать в непрерывном режиме, например чтобы распознать сакраментальную фразу «OK GOOGLE» без дополнительных действий со стороны пользователя. В области больших данных оптический сопроцессор поможет справиться с экспоненциально растущими объёмами информации в таких областях, как интернет вещей, исследования генома, распознавание видео.
Как это работает?
В статье рассматривается постановка задачи гребневой регрессии (ridge regression) с простенькой функцией ядра (kernel function), где эпсилон — это эллиптические интегралы.

Несмотря на устрашающий вид, эта функция имеет колоколообразный вид, описывает меру близости между векторами признаков и получена экспериментально из анализа оптической системы.
Гребневая регрессия является одним из простейших линейных классификаторов, её решение в аналитической форме зависит от внутреннего произведения матрицы векторов признаков XXT размерностью n x n:
Y' = X'XT(XXT + λI)-1Y
Здесь X — матрица обучающих признаков, Y — матрица классификации обучающих данных, X' — матрица тестовых признаков, Y' — искомая матрица классификации тестовых данных, I — единичная матрица, λ — коэффициент регуляризации.
Например, авторы статьи обучили линейный ридж-регрессионный классификатор MNIST в стандартном разбиении n=60000 обучающих и 10000 тестовых образцов; ошибка классификации составила 12%. При этом потребовалось инвертирование матрицы размерностью 60000х60000. Конечно, при работе с большими данными количество образцов может исчисляться миллиардами, и инвертирование (и даже просто хранение) матриц таких размеров невозможно.
Заменим теперь X на нелинейное отображение случайных проекций исходных признаков в пространство размерности N < n:
Kij = φ((WXi)j + bj) i=1..n, j=1..N
Здесь W — матрица случайных весов, b — вектор смещения, φ — нелинейная функция. Тогда, отобразив тестовые признаки X' в K', получим
Y' = K'KT(KKT + λI)-1Y
При обучении классификатора MNIST взяли N=10000 случайных проекций, W содержала случайные комплексные веса с вещественной и мнимой частью, распределенных по Гауссу, в качестве нелинейной функции использовали модуль. При этом ошибка классификации составила 2% (против 12% в линейном классификаторе), размерность обращаемой матрицы 10000 х 10000, более того, размерность не зависела от n2. Использование эллиптической функции ядра позволяет снизить ошибку до 1.3%. Конечно, применение более совершенных классификаторов типа сверточных нейронных сетей позволяет получить более высокую точность на MNIST, но в задачах больших данных или мобильных приложениях не всегда возможно использовать нейронные сети.
Описанный математический аппарат требует хранения и умножения исходных признаков на потенциально огромную случайную матрицу, и применения нелинейной функции к результату умножения. Авторы разработали экспериментальную установку, которая производит эти вычисления в аналоговой форме «со скоростью света».
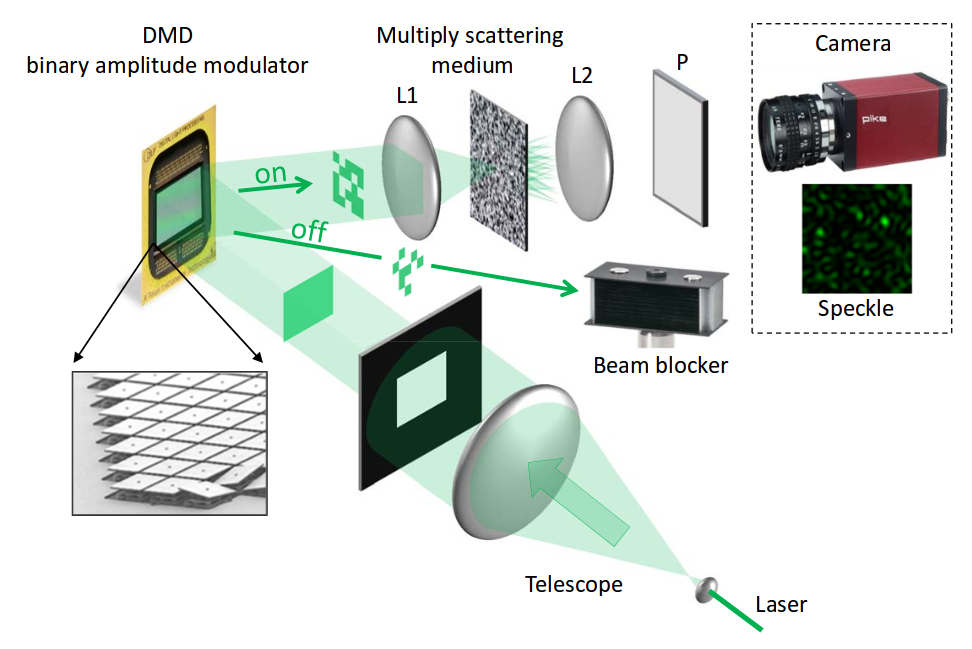
Монохромный лазерный луч 532 нм расширяют с помощью «телескопа», и полученным квадратным пучком освещают цифровую матрицу микрозеркал DMD. DMD пространственно кодирует световой пучок входными данными — признаками. Например, в случае задачи распознавания рукописных цифр MNIST коммерчески доступная матрица DMD размерностью 1920 х 1080 кодирует пикселы полутоновых изображений MNIST размерностью 28 х 28 таким образом, что каждому пикселу MNIST соответствует участок 4 х 4 микрозеркала, т. е. 16 уровней яркости.
Далее световой пучок, содержащий амплитудно-модулированный сигнал входного изображения, направляют на вещество, выполняющее роль случайной весовой матрицы проекции. Это толстый слой (десятки микрон) наночастиц диоксида титана, т. е. белый пигмент. Огромное количество непрозрачных частиц так перемешивают световой луч, что его свойства можно считать вполне случайными, но при этом детерминированными и повторяемыми (т. е. матрица W неизменна).
Поскольку световой пучок получен от лазера, он когерентный, и порождает интерференционную картину на матрице обычной видеокамеры. Эта интерференционная картина представляет собой набор случайных проекций высокой размерности (порядка 104 — 106), и следовательно его можно использовать для построения линейного классификатора, например SVM. За счёт высокой размерности и нелинейности шансы на линейную разделимость данных повышаются, и линейные классификаторы на основе таких интерференционных картин могут достигать точности, сравнимой с нейросетевыми. При этом скорость расчётов и энергозатраты несопоставимы. Скорость работы ограничена только быстродействием микрозеркал DMD и считывания интерференционной картины с видеокамеры. Современные матрицы достигают скорости работы 20 кГц. Реализация такой оптической системы в едином кристалле позволит действительно создать универсальный сопроцессор для эффективного извлечения признаков из разнообразных данных окружающего мира.
Оптическую схему авторы запатентовали для использования в задаче compressive sensing (публикация WO2013068783) и, возможно, для задачи классификации (публикации патентной заявки пока нет). Тем не менее, надеюсь, описанная методика породит новые идеи в хабраголовах.
Если вы хотите заниматься всякими такими штуками, приглашаю на стажировку или на постоянную работу в НИКФИ — научно-исследовательский кинофотоинститут.