Предисловие
Данный пост — краткий пересказ этого видео на английском.
Если нет времени читать — живой пример тут. В поле factor можно подставлять любые неотрицательные значения. Мои любимые — 51, 99, 106, 134, 150.
Если нет времени читать — живой пример тут. В поле factor можно подставлять любые неотрицательные значения. Мои любимые — 51, 99, 106, 134, 150.
Математика никогда не перестает удивлять своей красотой. Данный пост о том, как превратить такую простую операцию, как умножение в нечто удивительное.Теперь ответьте на вопрос — что общего между этим картинками?
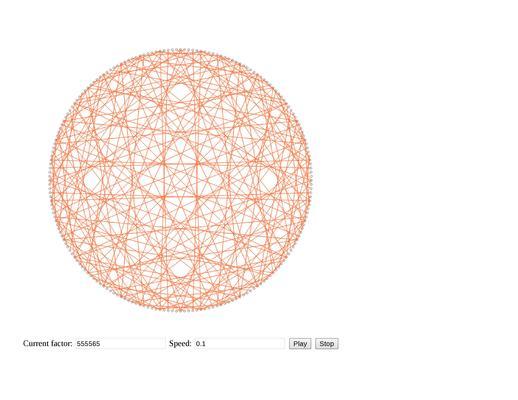
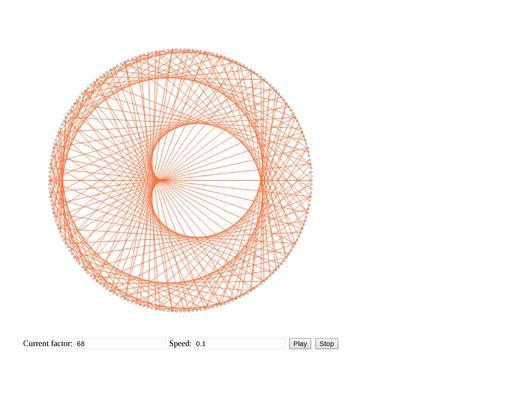

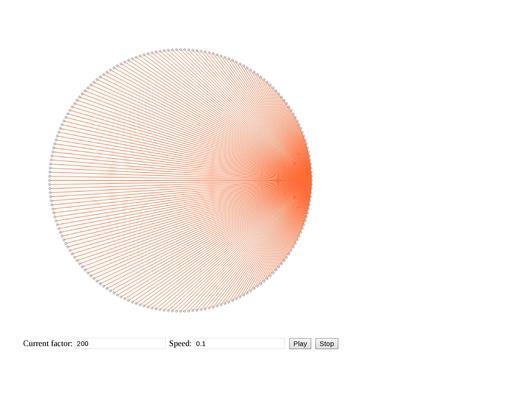
Все они созданы при помощи лишь одной операции — умножения (на самом деле, еще взятия остатка). Как же так, ведь они выглядят такими сложными и различными?
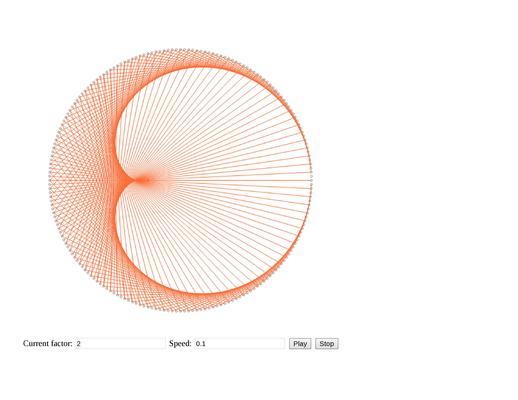
Алгоритм же довольно прост — нарисуем по кругу N точек на одинаковом расстоянии друг от друга. Чем больше точек, тем богаче и ярче будет конечный результат. В примерах N = 200. Все их обозначим числами от 0 до N-1. Дальше выберем любое неотрицательное число (сейчас для простоты возьмем натуральное). Пускай это будет 2. Теперь для каждой точки сделаем так — возьмем число, которым мы ее обозначили и умножим на 2. Получится новое число от 0 до 2(N-1). Это число будет обозначать другую точку, с которой мы соединим линией данную. Точка 0 будет соединена сама с собой, точка 1 с точкой 2, точка 2 с 4, 3 с 6 и т.д. Так мы дойдем до точки с номером 100. Умножив 100 на 2 получим 200 — а точки с таким номером-то у нас и нет. Самое логичное, что можно сделать — взять получившееся число по модулю N, т.е. в нашем случае 200, и получить 0. Значит 100 точку соединяем с 0.
В итоге у нас получится такая фигура, еще называемая кардиоидой из-за ее схожести с изображением сердца.
Теперь можно выбирать любые числа от 0 до N (после N фигуры начинают повторяться) и смотреть на результат. Что же делать, если мы выбрали дробное число? Ответ тоже прост — после умножения округлить результат вниз. Вследствие этого при выборе чисел 2.1 и 2.2 фигуры почти не будут отличаться, однако при дальнейшем увеличении (2.3, 2.4, 2.5… 2.9) все больше будут походить на фигуру, полученную при выборе числа 3. Благодаря этому создается эффект анимации, который вы можете понаблюдать в интерактивном примере, выставив factor на 2 (число, на которое мы умножаем) и speed на 0.02 (величина, которая прибавляется к factor каждый кадр).
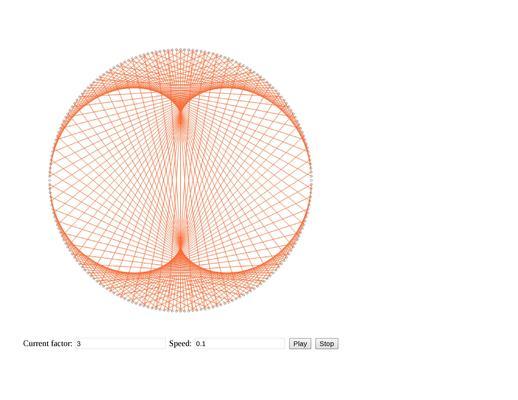
При выборе factor = 3
Делитесь вашими интересными factor'ами. Спасибо!