Часть 2 — градиентный спуск начало
В предыдущей части я начал разбор алгоритма оптимизации под названием градиентный спуск. Предыдущая статья оборвалась на писании варианта алгоритма под названием пакетный градиентный спуск.
Существует и другая версия алгоритма — стохастический градиентный спуск. Стохастический = случайный.
Также напомню как выглядит пакетный:
Формулы похожи, но, как видно, пакетный градиентный спуск вычисляет один шаг, используя сразу весь набор данных, тогда как стохастический за шаг использует только 1 элемент. Можно два этих варианта скрестить, получив мини-пакетный (mini-batch) спуск, который за раз обрабатывает, к примеру, 100 элементов, а не все или один.
Два этих варианта ведут себя похоже, но не одинаково. Пакетный спуск действительно следует в направлении наискорейшего спуска, тогда как стохастический, используя только один элемент из обучающей выборки, не может верно вычислить градиент для всей выборки. Это различие проще пояснить графически. Для этого я модифицирую код из первой части, в котором вычислялись коэффициенты линейной регрессии. Функция стоимости для нее выглядит следующим образом:
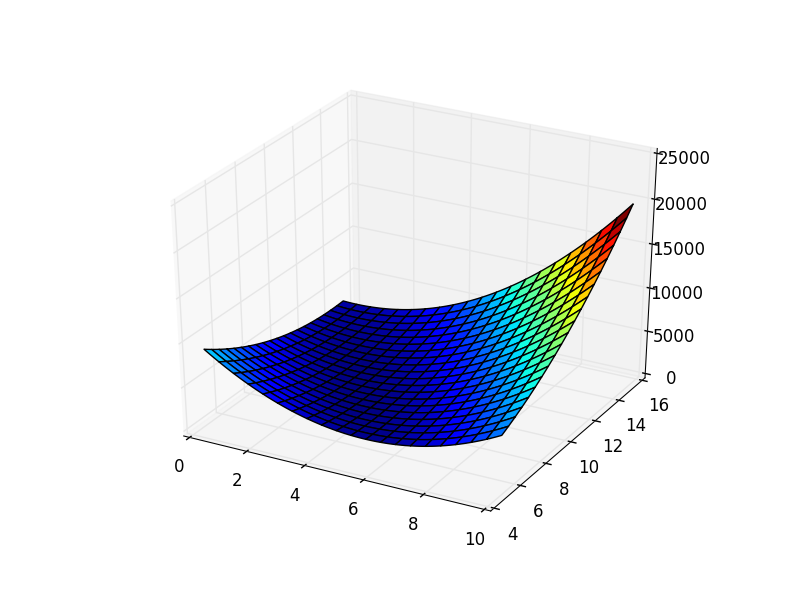
Как видно, это немного вытянутый параболоид. И также его «вид сверху», где крестом отмечен истинный минимум, найденный аналитически.
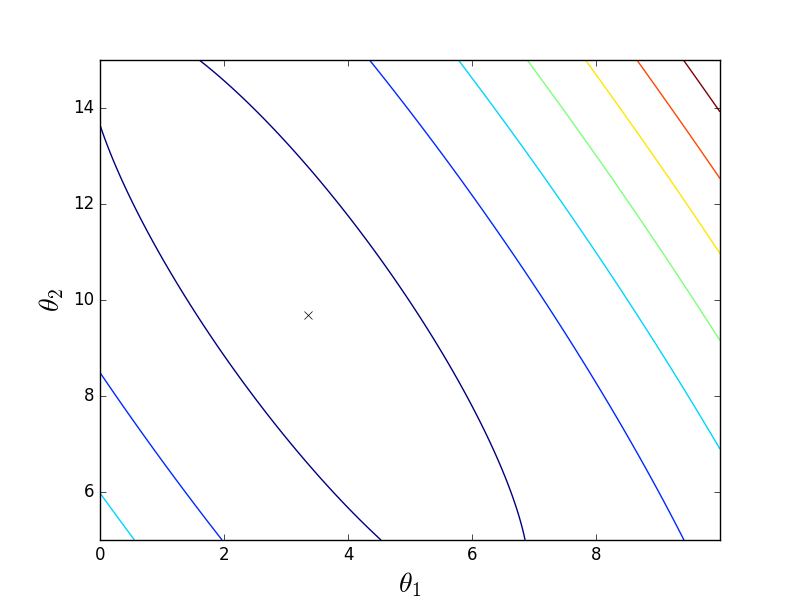
Сперва рассмотрим, как ведет себя пакетный спуск:
Из-за того, что параболоид вытянутый, по его «дну» проходит «овраг», в который мы попадаем. Из-за этого последние шаги вдоль этого оврага очень маленькие, но тем не менее рано или поздно градиентный спуск доберется до минимума. Спуск происходит по линии антиградиента, каждый шаг приближаясь к минимуму.
Теперь та же самая функция, но для стохастического спуска:
В определении сказано, что выбирается только один элемент — в этом коде каждый последующий элемент выбирается случайным образом.
Как видно, в случае стохастического варианта, спуск идет не по линии антиградиента, а вообще непонятно как — каждый шаг отклоняясь в случайную сторону. Может показаться, что такими случайными дергаными движениями к минимуму можно прийти только случайно, однако было доказано, что стохастический градиентный спуск сходится почти наверное. Пару ссылок, например.
На 200 элементах разницы в скорости почти никакой нет, однако, увеличив количество элементов до 2000 (что тоже очень мало) и подкорректировав скорость обучения, стохастический вариант бьет пакетный, как хочет. Однако, в силу стохастической природы, иногда метод промахивается, осциллируя возле минимума без возможности остановиться. Как-то так:
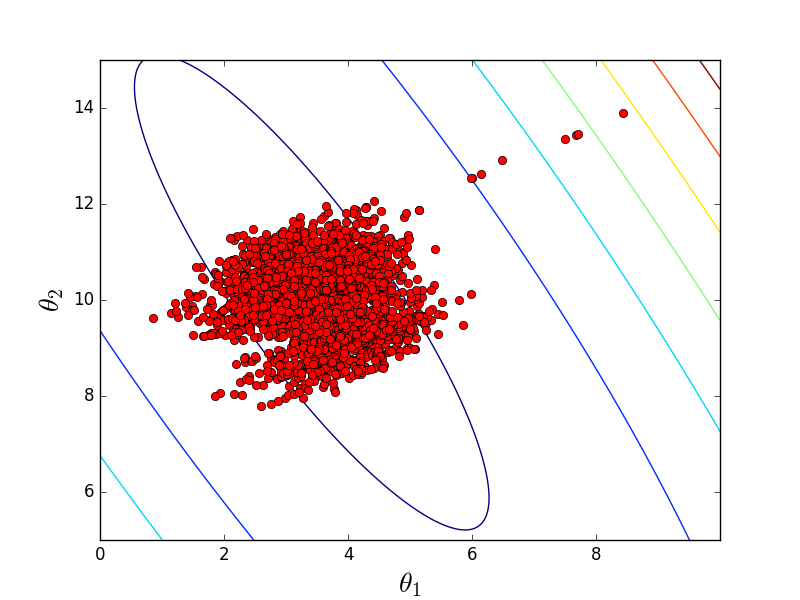
Этот факт делает неприменимой чистую реализацию. Чтобы как-то призвать к порядку и снизить «случайность» можно снизить скорость обучения. На практике применяют mini-batch вариацию — от стохастической она отличается тем, что вместо одного случайно выбранного элемента выбирают больше одного.
О разнице, плюсах и минусах данных двух подходов написано достаточно много, вкратце подведу итог:
— Пакетный спуск хорош для строго выпуклых функций, потому что уверенно стремится к минимуму глобальному или локальному.
— Стохастический в свою очередь лучше работает на функциях с большим количеством локальных минимумов — каждый шаг есть шанс, что очередное значение «выбьет» из локальной ямы и конечное решение будет более оптимальным, нежели для пакетного спуска.
— Стохастический вычисляется быстрее — на каждом шаге нужны не все элементы из выборки. Вся выборка целиком может не влезть в память. Но требуется больше шагов.
— Для стохастического легко добавить новые элементы во время работы («онлайн» обучение).
— В случае mini-batch, можно также векторизовать код, что значительно ускорит его выполнение.
Также у градиентного спуска существует множество модификаций — momentum, наискорейшего спуска, усреднение, Adagrad, AdaDelta, RMSProp и другие. Здесь можно посмотреть короткий обзор некоторых. Частенько они используют значения градиента с предыдущих шагов или автоматически вычисляют наилучшее значение скорости для данного шага. Использование этих методов для простой гладкой функции МНК не имеет особого смысла, но в случае нейронных сетей и сетей с большим количеством слоев\нейронов, функция стоимости становится совсем грустной и градиентный спуск может застрять в локальной яме, так и не достигнув оптимального решения. Для таких проблем подходят методы на стероидах. Вот пример функции простой для минимизации (двумерная линейная регрессия с МНК):
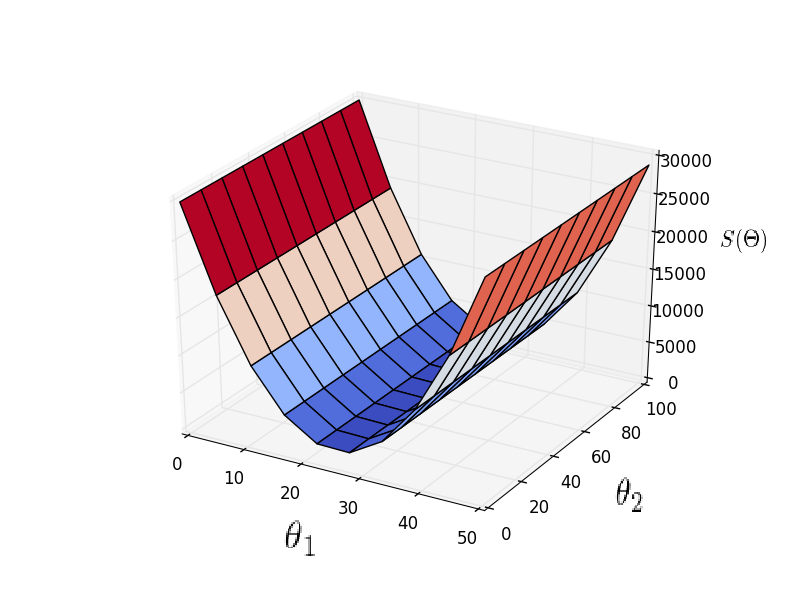
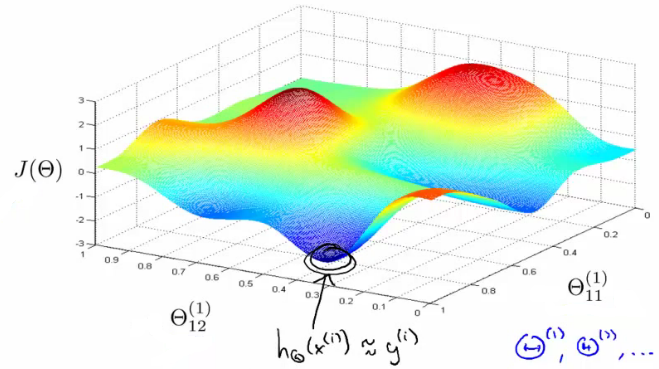
И пример нелинейной функции:
Градиентный спуск — метод оптимизации первого порядка (первая производная). Также существует много методов второго порядка — для них необходимо вычислять вторую производную и строить гессиан (довольно затратная операция —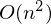 ). Например, градиентный спуск второго порядка (скорость обучения заменили на гессиан), BFGS, сопряженные градиенты, метод Ньютона и еще огромное количество других методов. В общем, оптимизация — это отдельный и очень широкий пласт проблем. Впрочем, вот пример (правда, всего лишь презентация) работы + видео Яна Лекуна, в который он говорит, что можно не парится и просто использовать градиентные методы. Даже учитывая, что презентация 2007 года, многие последние эксперименты с большими ИНС использовали градиентные методы. Например.
). Например, градиентный спуск второго порядка (скорость обучения заменили на гессиан), BFGS, сопряженные градиенты, метод Ньютона и еще огромное количество других методов. В общем, оптимизация — это отдельный и очень широкий пласт проблем. Впрочем, вот пример (правда, всего лишь презентация) работы + видео Яна Лекуна, в который он говорит, что можно не парится и просто использовать градиентные методы. Даже учитывая, что презентация 2007 года, многие последние эксперименты с большими ИНС использовали градиентные методы. Например.
На голых циклах далеко не уедешь — код нуждается в векторизации. Основной алгоритм для векторизации — пакетный градиентный спуск, с оговоркой, что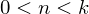 , где k — количество элементов в тестовой выборке. Таким образом векторизация подходит для mini-batch метода. Как и в прошлый раз я выпишу все в раскрытых векторах. Обратите внимание что первая матрица транспонирована —
, где k — количество элементов в тестовой выборке. Таким образом векторизация подходит для mini-batch метода. Как и в прошлый раз я выпишу все в раскрытых векторах. Обратите внимание что первая матрица транспонирована — 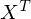
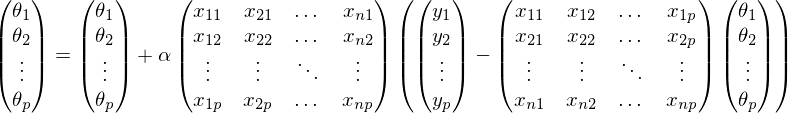
Для доказательства, пройдем пару шагов в обратную сторону:
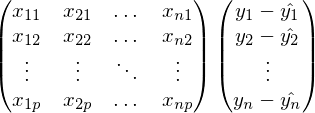
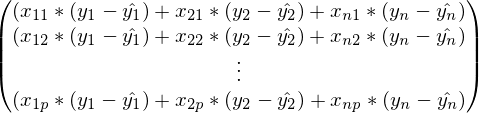
В предыдущей формуле, в каждой строке индекс j зафиксирован, а i — изменяется от 1 до n. Свернув сумму:
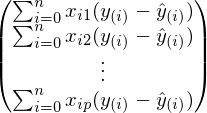
Это выражение точно такое же, что и в определении градиентного спуска. Наконец, завершающий шаг — сворачивание векторов и матриц:
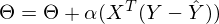
Стоимость одного такого шага —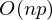 , где n — количество элементов, p — количество признаков. Много лучше
, где n — количество элементов, p — количество признаков. Много лучше 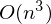 . Также встречается выражение, тождественное этому:
. Также встречается выражение, тождественное этому:

Обратите внимание, что поменялись местами предсказанное значение и реальное, что привело к изменению знака перед скоростью обучения.
» Для запуска примеров необходимы: numpy, matplotlib.
» Материалы, использованные в статье — github.com/m9psy/neural_network_habr_guide
В предыдущей части я начал разбор алгоритма оптимизации под названием градиентный спуск. Предыдущая статья оборвалась на писании варианта алгоритма под названием пакетный градиентный спуск.
Существует и другая версия алгоритма — стохастический градиентный спуск. Стохастический = случайный.
Повторять, пока не сойдется
{
for i in train_set
{
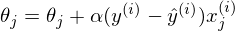
}
}
Также напомню как выглядит пакетный:
Повторять, пока не сойдется
{
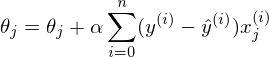
}
Формулы похожи, но, как видно, пакетный градиентный спуск вычисляет один шаг, используя сразу весь набор данных, тогда как стохастический за шаг использует только 1 элемент. Можно два этих варианта скрестить, получив мини-пакетный (mini-batch) спуск, который за раз обрабатывает, к примеру, 100 элементов, а не все или один.
Два этих варианта ведут себя похоже, но не одинаково. Пакетный спуск действительно следует в направлении наискорейшего спуска, тогда как стохастический, используя только один элемент из обучающей выборки, не может верно вычислить градиент для всей выборки. Это различие проще пояснить графически. Для этого я модифицирую код из первой части, в котором вычислялись коэффициенты линейной регрессии. Функция стоимости для нее выглядит следующим образом:

Как видно, это немного вытянутый параболоид. И также его «вид сверху», где крестом отмечен истинный минимум, найденный аналитически.

Сперва рассмотрим, как ведет себя пакетный спуск:
Код
def batch_descent(A, Y, speed=0.001):
theta = np.array(INITIAL_THETA.copy(), dtype=np.float32)
theta.reshape((len(theta), 1))
previous_cost = 10 ** 6
current_cost = cost_function(A, Y, theta)
while np.abs(previous_cost - current_cost) > EPS:
previous_cost = current_cost
derivatives = [0] * len(theta)
# ---------------------------------------------
for j in range(len(theta)):
summ = 0
for i in range(len(Y)):
summ += (Y[i] - A[i]@theta) * A[i][j]
derivatives[j] = summ
# Выполнение требования одновремменности
theta[0] += speed * derivatives[0]
theta[1] += speed * derivatives[1]
# ---------------------------------------------
current_cost = cost_function(A, Y, theta)
print("Batch cost:", current_cost)
plt.plot(theta[0], theta[1], 'ro')
return theta
Пакетный-анимация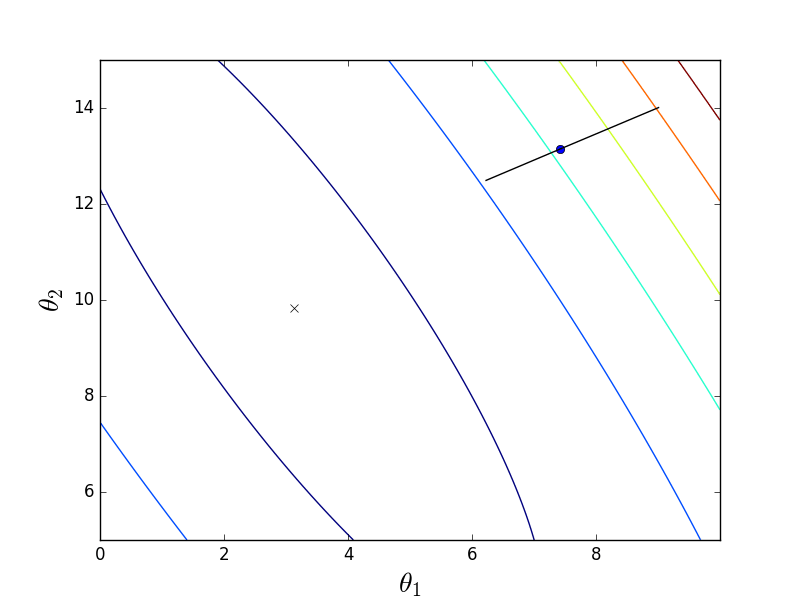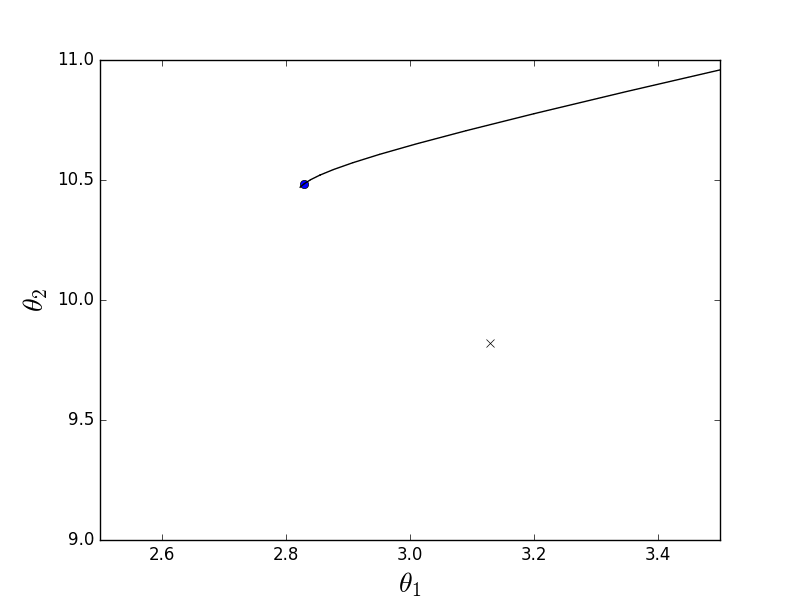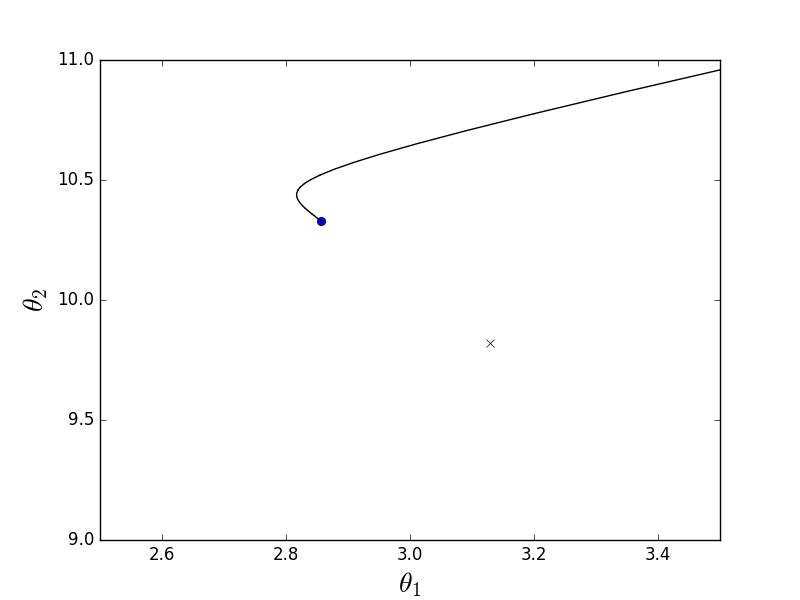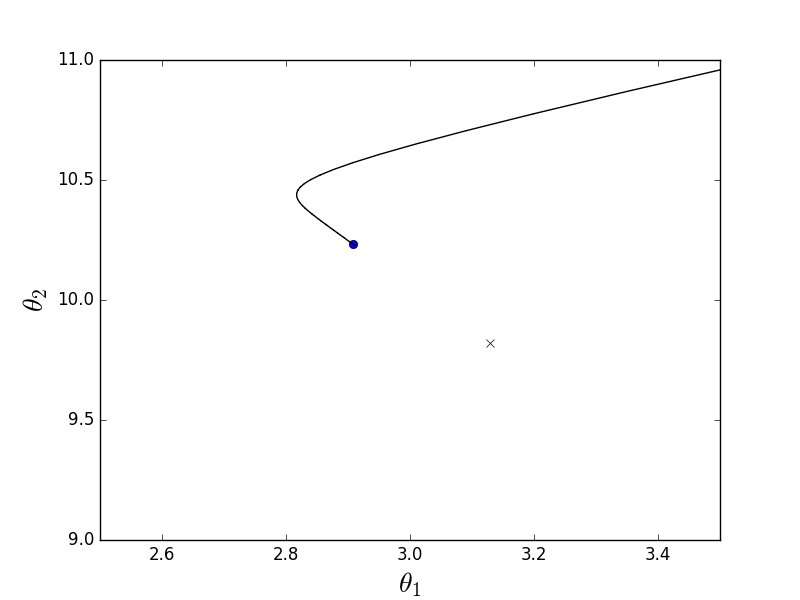

Из-за того, что параболоид вытянутый, по его «дну» проходит «овраг», в который мы попадаем. Из-за этого последние шаги вдоль этого оврага очень маленькие, но тем не менее рано или поздно градиентный спуск доберется до минимума. Спуск происходит по линии антиградиента, каждый шаг приближаясь к минимуму.
Теперь та же самая функция, но для стохастического спуска:
Код
def stochastic_descent(A, Y, speed=0.1):
theta = np.array(INITIAL_THETA.copy(), dtype=np.float32)
previous_cost = 10 ** 6
current_cost = cost_function(A, Y, theta)
while np.abs(previous_cost - current_cost) > EPS:
previous_cost = current_cost
# --------------------------------------
# for i in range(len(Y)):
i = np.random.randint(0, len(Y))
derivatives = [0] * len(theta)
for j in range(len(theta)):
derivatives[j] = (Y[i] - A[i]@theta) * A[i][j]
theta[0] += speed * derivatives[0]
theta[1] += speed * derivatives[1]
current_cost = cost_function(A, Y, theta)
print("Stochastic cost:", current_cost)
plt.plot(theta[0], theta[1], 'ro')
# --------------------------------------
current_cost = cost_function(A, Y, theta)
return theta
В определении сказано, что выбирается только один элемент — в этом коде каждый последующий элемент выбирается случайным образом.
Стохастический-анимация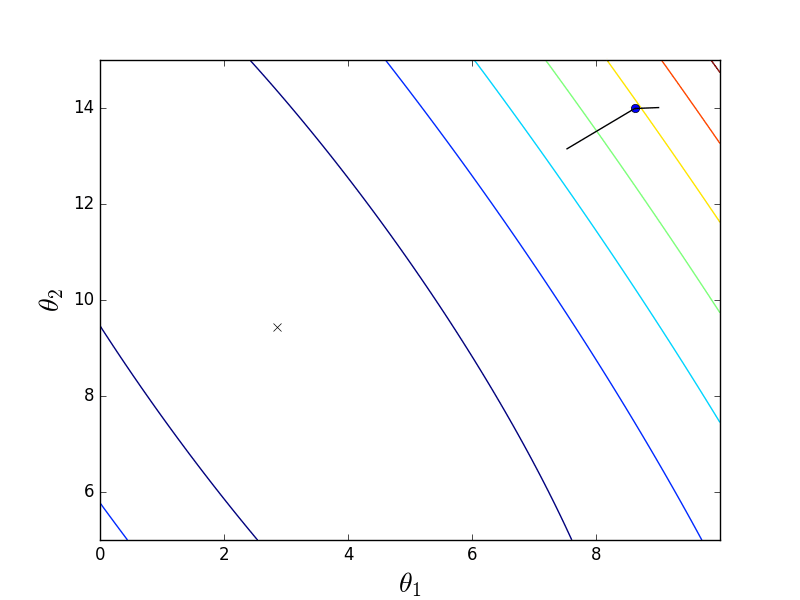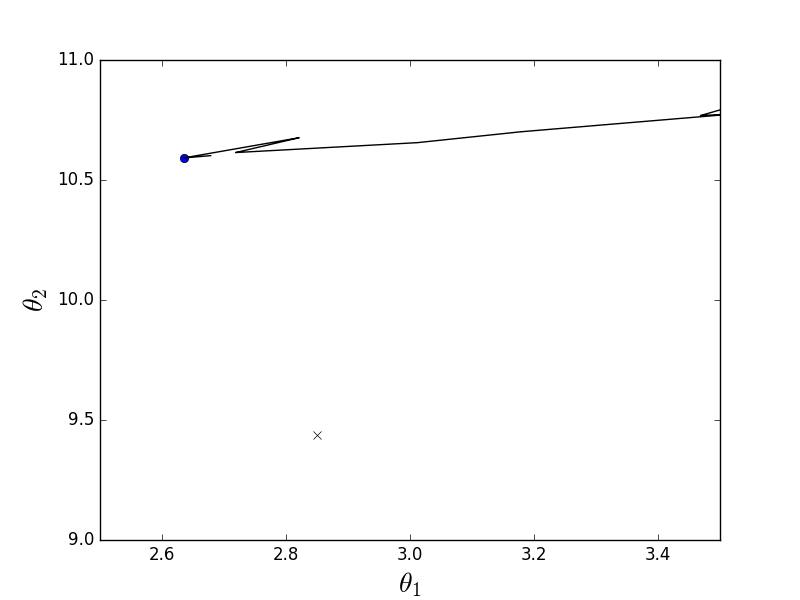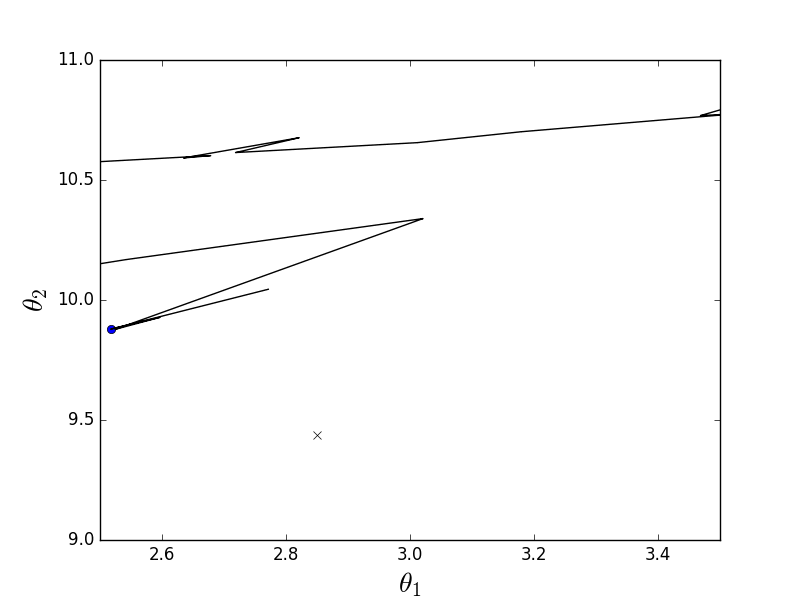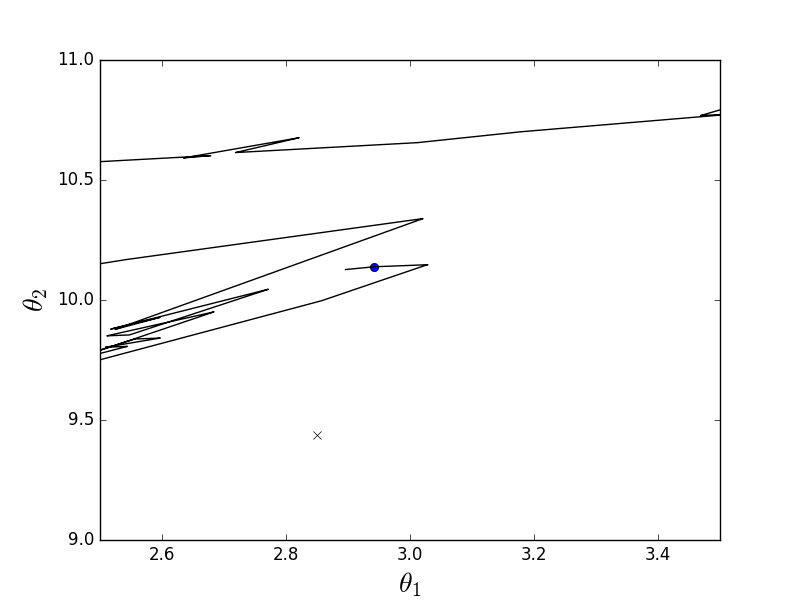

Как видно, в случае стохастического варианта, спуск идет не по линии антиградиента, а вообще непонятно как — каждый шаг отклоняясь в случайную сторону. Может показаться, что такими случайными дергаными движениями к минимуму можно прийти только случайно, однако было доказано, что стохастический градиентный спуск сходится почти наверное. Пару ссылок, например.
Весь код целиком
import numpy as np
import matplotlib.pyplot as plt
TOTAL = 200
STEP = 0.25
EPS = 0.1
INITIAL_THETA = [9, 14]
def func(x):
return 0.2 * x + 3
def generate_sample(total=TOTAL):
x = 0
while x < total * STEP:
yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)
x += STEP
def cost_function(A, Y, theta):
return (Y - A@theta).T@(Y - A@theta)
def batch_descent(A, Y, speed=0.001):
theta = np.array(INITIAL_THETA.copy(), dtype=np.float32)
theta.reshape((len(theta), 1))
previous_cost = 10 ** 6
current_cost = cost_function(A, Y, theta)
while np.abs(previous_cost - current_cost) > EPS:
previous_cost = current_cost
derivatives = [0] * len(theta)
# ---------------------------------------------
for j in range(len(theta)):
summ = 0
for i in range(len(Y)):
summ += (Y[i] - A[i]@theta) * A[i][j]
derivatives[j] = summ
# Выполнение требования одновремменности
theta[0] += speed * derivatives[0]
theta[1] += speed * derivatives[1]
# ---------------------------------------------
current_cost = cost_function(A, Y, theta)
print("Batch cost:", current_cost)
plt.plot(theta[0], theta[1], 'ro')
return theta
def stochastic_descent(A, Y, speed=0.1):
theta = np.array(INITIAL_THETA.copy(), dtype=np.float32)
previous_cost = 10 ** 6
current_cost = cost_function(A, Y, theta)
while np.abs(previous_cost - current_cost) > EPS:
previous_cost = current_cost
# --------------------------------------
# for i in range(len(Y)):
i = np.random.randint(0, len(Y))
derivatives = [0] * len(theta)
for j in range(len(theta)):
derivatives[j] = (Y[i] - A[i]@theta) * A[i][j]
theta[0] += speed * derivatives[0]
theta[1] += speed * derivatives[1]
# --------------------------------------
current_cost = cost_function(A, Y, theta)
print("Stochastic cost:", current_cost)
plt.plot(theta[0], theta[1], 'ro')
return theta
X = np.arange(0, TOTAL * STEP, STEP)
Y = np.array([y for y in generate_sample(TOTAL)])
# Нормализацию вкрячил, чтобы парабалоид красивый был
X = (X - X.min()) / (X.max() - X.min())
A = np.empty((TOTAL, 2))
A[:, 0] = 1
A[:, 1] = X
theta = np.linalg.pinv(A).dot(Y)
print(theta, cost_function(A, Y, theta))
import time
start = time.clock()
theta_stochastic = stochastic_descent(A, Y, 0.001)
print("St:", time.clock() - start, theta_stochastic)
start = time.clock()
theta_batch = batch_descent(A, Y, 0.001)
print("Btch:", time.clock() - start, theta_batch)
На 200 элементах разницы в скорости почти никакой нет, однако, увеличив количество элементов до 2000 (что тоже очень мало) и подкорректировав скорость обучения, стохастический вариант бьет пакетный, как хочет. Однако, в силу стохастической природы, иногда метод промахивается, осциллируя возле минимума без возможности остановиться. Как-то так:

Этот факт делает неприменимой чистую реализацию. Чтобы как-то призвать к порядку и снизить «случайность» можно снизить скорость обучения. На практике применяют mini-batch вариацию — от стохастической она отличается тем, что вместо одного случайно выбранного элемента выбирают больше одного.
О разнице, плюсах и минусах данных двух подходов написано достаточно много, вкратце подведу итог:
— Пакетный спуск хорош для строго выпуклых функций, потому что уверенно стремится к минимуму глобальному или локальному.
— Стохастический в свою очередь лучше работает на функциях с большим количеством локальных минимумов — каждый шаг есть шанс, что очередное значение «выбьет» из локальной ямы и конечное решение будет более оптимальным, нежели для пакетного спуска.
— Стохастический вычисляется быстрее — на каждом шаге нужны не все элементы из выборки. Вся выборка целиком может не влезть в память. Но требуется больше шагов.
— Для стохастического легко добавить новые элементы во время работы («онлайн» обучение).
— В случае mini-batch, можно также векторизовать код, что значительно ускорит его выполнение.
Также у градиентного спуска существует множество модификаций — momentum, наискорейшего спуска, усреднение, Adagrad, AdaDelta, RMSProp и другие. Здесь можно посмотреть короткий обзор некоторых. Частенько они используют значения градиента с предыдущих шагов или автоматически вычисляют наилучшее значение скорости для данного шага. Использование этих методов для простой гладкой функции МНК не имеет особого смысла, но в случае нейронных сетей и сетей с большим количеством слоев\нейронов, функция стоимости становится совсем грустной и градиентный спуск может застрять в локальной яме, так и не достигнув оптимального решения. Для таких проблем подходят методы на стероидах. Вот пример функции простой для минимизации (двумерная линейная регрессия с МНК):

И пример нелинейной функции:

Градиентный спуск — метод оптимизации первого порядка (первая производная). Также существует много методов второго порядка — для них необходимо вычислять вторую производную и строить гессиан (довольно затратная операция —
 ). Например, градиентный спуск второго порядка (скорость обучения заменили на гессиан), BFGS, сопряженные градиенты, метод Ньютона и еще огромное количество других методов. В общем, оптимизация — это отдельный и очень широкий пласт проблем. Впрочем, вот пример (правда, всего лишь презентация) работы + видео Яна Лекуна, в который он говорит, что можно не парится и просто использовать градиентные методы. Даже учитывая, что презентация 2007 года, многие последние эксперименты с большими ИНС использовали градиентные методы. Например.
). Например, градиентный спуск второго порядка (скорость обучения заменили на гессиан), BFGS, сопряженные градиенты, метод Ньютона и еще огромное количество других методов. В общем, оптимизация — это отдельный и очень широкий пласт проблем. Впрочем, вот пример (правда, всего лишь презентация) работы + видео Яна Лекуна, в который он говорит, что можно не парится и просто использовать градиентные методы. Даже учитывая, что презентация 2007 года, многие последние эксперименты с большими ИНС использовали градиентные методы. Например.На голых циклах далеко не уедешь — код нуждается в векторизации. Основной алгоритм для векторизации — пакетный градиентный спуск, с оговоркой, что
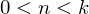 , где k — количество элементов в тестовой выборке. Таким образом векторизация подходит для mini-batch метода. Как и в прошлый раз я выпишу все в раскрытых векторах. Обратите внимание что первая матрица транспонирована —
, где k — количество элементов в тестовой выборке. Таким образом векторизация подходит для mini-batch метода. Как и в прошлый раз я выпишу все в раскрытых векторах. Обратите внимание что первая матрица транспонирована — 
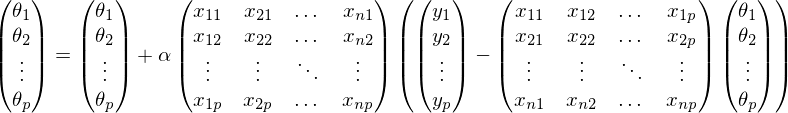
Для доказательства, пройдем пару шагов в обратную сторону:

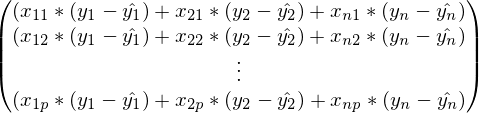
В предыдущей формуле, в каждой строке индекс j зафиксирован, а i — изменяется от 1 до n. Свернув сумму:
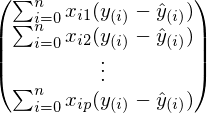
Это выражение точно такое же, что и в определении градиентного спуска. Наконец, завершающий шаг — сворачивание векторов и матриц:

Стоимость одного такого шага —
 , где n — количество элементов, p — количество признаков. Много лучше
, где n — количество элементов, p — количество признаков. Много лучше 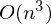 . Также встречается выражение, тождественное этому:
. Также встречается выражение, тождественное этому:
Обратите внимание, что поменялись местами предсказанное значение и реальное, что привело к изменению знака перед скоростью обучения.
» Для запуска примеров необходимы: numpy, matplotlib.
» Материалы, использованные в статье — github.com/m9psy/neural_network_habr_guide

