Введение
Готовясь к редизайну и пересмотру сайта wufoo.com, я посвятил некоторое время повторному изучению основ взаимодействия человека и компьютера, в надежде вобрать что-то новое, что накопилось за десятилетия исследований в области создания простых интерфейсов. Первое, что меня удивило на этом пути — это то, что материал по данной теме был крайне сжат и явно ориентировался на математиков, поскольку был написан на языке академической элиты. Можно предположить, что если бы они хотели произвести впечатление (особенно на дизайнеров), они могли бы написать документы, более лёгкие для восприятия.
Вспоминая школу, я отметил, что лишь во время изучения физики математика приобрела для меня некий смысл. Вместо абстрактных функций мне были нужны графики. Размышляя в таком ключе я подумал, что было бы неплохо дать наглядную интерпретацию закону Фиттса — краеугольному камню проектирования человеко-машинных интерфейсов, и объяснить как его концепцию, так и то, почему эти идеи чуть более сложны, чем многим бы того хотелось
Математика очевидного
Опубликованный в 1954 году закон Фиттса — это эффективный метод моделирования специфичной, и вместе с тем очень распространённой ситуации, возникающей при разработке интерфейсов. Эта ситуация включает в себя объект, управляемый человеком (будь то физический, в виде пальца, или виртуальный, как курсор мыши) и цели, расположенной где-то ещё. Именно эту ситуацию иллюстрирует первая диаграмма:

Математически закон Фиттса можно записать так:
T = a + b log2(D/W + 1),
где T — среднее время, затрачиваемое на совершение действия, a — время запуска/остановки устройства, b — величина, зависящая от типичной скорости устройства, D — дистанция от точки старта до центра объекта, W — ширина объекта, измеренная вдоль оси движения.
Главным образом это означает, что время, затрачиваемое на достижение цели, является функцией расстояния и размера цели. На первый взгляд это кажется очевидным: чем дальше мы от цели и чем меньше она по размеру, тем больше времени потребуется для позиционирования. Том Стэффорд развивает эту мысль:
«Хотя основной посыл и очевиден (большие вещи легче выбрать), точная математическая характеристика впечатляет, так как включает в себя логарифмическую функцию, а это означает, что взаимосвязь между размером и временем реакции такова, что небольшое увеличение размеров малых объектов позволяет их легче выделять (тогда как небольшое изменение размеров больших объектов уже не имеет значения). То же самое касается и дистанции до цели»
Переходя к реальному миру, можно сказать, что гораздо легче указать на монету, чем на веснушку, а вот показать на дом или на жилой комплекс — уже практически без разницы. Таким образом, когда вы в очередной раз будете оптимизировать свой веб сайт по закону Фиттса, запомните, что если ссылка уже немаленькая, то дальнейшее её увеличение скорость доступа к ней не увеличит. Вместе с тем, даже небольшое увеличение размера маленьких ссылок уже имеет значение.
Закон Фиттса касается линий!
Желая извлечь практический урок из уравнения Фиттса, дизайнеры интерфейсов вывели несколько правил практического применения одного из немногих законов взаимодействия человека и компьютера. Одно из правил называется
Правило размера цели
Оно сочетает в себе идеи, приводящие закон Фиттса и закон Хика (о котором речь пойдёт в другой раз) к утверждению, что размер кнопки должен быть пропорционален частоте её использования. Брюс Тогнаццини, гуру интерфейсов из Apple, даже разработал великолепную викторину, чтобы объяснить, как закон Фиттса может быть использован для разработки правил, радикально улучшающих интерфейсы операционных систем.
Перед тем, как вы пойдёте и станете слепо применять эти правила в своих приложениях, мне бы хотелось напомнить, что закон Фиттса описывает очень специфическую ситуацию. Он отталкивается от предположения, что движение из стартовой точки является четким и направленным, а это подразумевает строго заданную и прямую траекторию (начинающуюся с высокой начальной скоростью, как если бы другие цели отсутствовали, и вы точно знали, куда вам нужно). Также я видел, что многие люди, думают, что закон Фиттса описывает следующую ситуацию:

Однако в вышеприведённом уравнении нет величины, соответствующей высоте цели, в него входит лишь ширина! Таким образом, раз уж мы завели речь об ограничениях закона Фиттса применительно к интерфейсам, можно сказать, что он описывает одномерную ситуацию. В оригинальных экспериментах Фиттса изучалась производительность человека при выполнении горизонтальных движений к цели. И амплитуда движений, и ширина окончательной области измерялись вдоль одних и тех же осей, что означает, что модель, описывающая закон, скорее выглядит так:

Таким образом, строя оптимизацию размера по закону Фиттса, можно предположить, что вертикальные и диагональные движения описываются теми же самыми уравнениями. При этом получится, что лёгкость, с которой можно указать на отдельную цель, на самом деле зависит от взаимного расположения точки старта и цели.
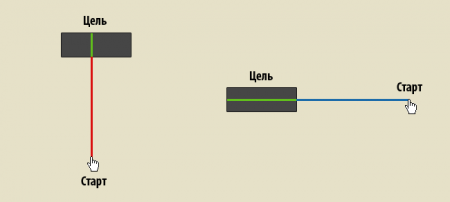
В вышеприведённом примере курсор справа, благодаря большей ширине, технически находится в более благоприятной ситуации для попадания в цель, нежели в ситуации слева. Заметьте, что закон Фиттса будет также хорошо работать и для круглых целей, поскольку расстояние до центра будет одинаковым для любых углов. Однако закон становится менее точным для прямоугольных и более сложных объектов. В следующем примере мы сделаем две попытки оптимизировать область ссылки путём увеличения размеров прямоугольника.
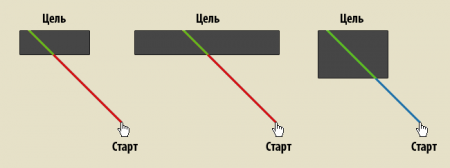
В первом случая мы увеличили ширину целевого прямоугольника, а во втором — высоту. Как можно заметить, для данной точки старта не все увеличения размера возымели эффект в виде более лёгкого попадания в цель, что может быть существенным для веб дизайнеров, работающих с использованием CSS и Box Model.
Позиционирование физическое и виртуальное
С момента публикации работы Фиттса были выполнены сотни производных экспериментов. Одна интересная работа была проведена в 1996 Эваном Грэмом и Кристин МакКензи, в которой анализировалось различие между позиционированием объектов в реальном и виртуальном мире. В ней показано, что движение из стартовой точки в целевую область может быть разделено на две части: начальную высокоскоростную фазу, и фазу замедления.

В данном исследовании авторы пришли к выводу, что на первую фазу влияет преимущественно расстояние до цели. Ни масштаб изображения, ни размер объекта не ускорят приближение к цели (ссылки большего размера не увеличат скорость движения). Единственная фаза, которая влияет на время выбора небольших объектов при одинаковых расстояниях — это фаза замедления. А вот теперь интересное:
«Различие между виртуальным и физическим отображением проявляется только на второй фазе движения, когда визуальное управление замедлением к небольшим целям — это виртуальная задача, занимающая больше времени, чем физическая»
Проще говоря, на ссылки и кнопки на экране проще нажать пальцем, а не мышью. И проблема с мышью упирается не в её способности попасть в цель, а в нашу способность точно замедлиться. Apple, на твои мониторы с мультитачем вся надежда.
Правило бесконечной границы
Из него следует, что мониторы компьютеров дают очень интересный побочный эффект из модели выбора цели по Фиттсу, поскольку у них есть нечто, называемое «краями». Джефф Атвуд, автор книги Ужас кодирования, действительно объяснил это практически великолепно в своей прошлогодней статье Закон Фиттса и бесконечная ширина.
Поскольку указательное устройство может уходить сколь угодно далеко в любом направлении, цели по краям экрана на деле являются целями с бесконечной шириной, как это показано ниже.
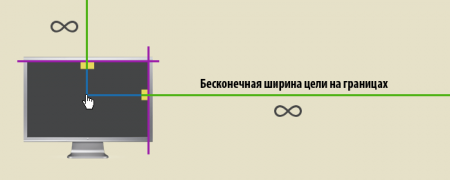
Для операционной системы и любого полноэкранного приложения эти границы обычно рассматриваются как наиболее ценное место, поскольку технически они наиболее доступны. Не только потому, что у них бесконечная ширина, но также и потому, что они не требуют от пользователя фазы торможения при их достижении. Вот почему так невероятно просто и интуитивно назначить действия вроде навигации между окнами на углы экрана (как это сделано в Compiz Fusion — прим. пер.)
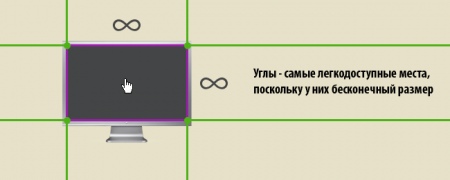
К сожалению, веб-приложения лишены преимуществ, которые даёт Правило бесконечных границ. Имея ограничение в виде необходимости запуска в окне браузера с границами, расположение кнопок и ссылок по краям и углам не представляет особого интереса с точки зрения закона Фиттса, если только браузер не запущен в полноэкранном режиме, что более характерно, пожалуй, лишь для веб-киосков.

Это также объясняет, почему интерфейсы операционных систем на базе веб-технологий никогда не будут так же хороши как те, что используют преимущества всей площади монитора.
Фиттс по-прежнему рулит!
Несколько вышеупомянутых ограничений закона Фиттса совершенно не повод, чтобы выбросить его в окно. Я лишь хотел показать, что дискуссии вокруг него не утихают и по сей день, как и 50 лет назад. И коль скоро он не может технически точно описать большинство ситуаций в области интерфейсов — люди не всегда уверенно движутся к цели, мы не используем прямых траекторий, обычно есть несколько целей, что может приводить к замешательству и так далее — не похоже, чтобы значительно более точные модели, учитывающие многие другие факторы, могли изменить фундаментальные истины, лежащие в основе закона Фиттса.
«Было показано, что закон Фиттса применим ко множеству случаев, включая различные конечности (руки, ноги, детекторы взгляда), манипуляторы, физические среды (включая подводную) и группы пользователей (молодые, старые, люди с замедленной реакцией и даже под воздействием наркотиков)»
В заключение, главная идея, которую мне бы хотелось, чтобы вынесли дизайнеры — это то, что задача разработки дизайна приложений столь сложна и насыщенна, включает в себя такое большое количество переменных, что следует с осторожностью относиться к всеобъемлющему применению закона Фиттса. С увеличением размеров мониторов, ростом популярности способов увеличить ускорение мыши, а также технологий пролистывания на больших экранах, интересно будет увидеть, как разработчики программного обеспечения смогут извлечь из этого пользу и увеличить возможность быстро преодолевать большие дистанции.