Эта история началась с того что я застрял в пробке на хайвее, не особенно большой, но полчаса простоял практически на месте. И, как это часто бывает, пробка рассосалась сама по себе — не было впереди ни аварии, ни ремонта, просто машины в какой-то момент начали двигаться быстрее, еще быстрее, и все — свободная дорога впереди.
Чем обычно занимаются в пробках? Ну кто-чем и когда-как, а я в тот день был в мирном философском настроении — просто сидел и размышлял. Вспомнил в частности пост на Гиктаймс о робомобилях где в комментариях бурно сравнивали манеру вождения людей и роботов и в конце кажется пришли к выводу что будущее на дорогах за AI, при нем и движение станет безопаснее и средняя скорость возрастет. Интересно, а пробки тогда будут? Другими словами, насколько пробки обусловлены внешними (обьективными) обстоятельствами, и насколько эффектом толпы, агрессивной или наоборот тормозной манерой вождения? Заодно вспомнилась прочитанная когда-то книга где утверждалось что моделирование дорожного трафика — одна из самых сложных математических задач, которая до сих пор не решена. Ну это наверное давно уже неправда, читал я это давно и книга уже тогда была не новой, сейчас уже наверняка и теории правильные написали, и на компьютерах своих все посчитали. Хотя… пробки же остались? В общем, полет фантазии было уже не остановить.
Итак, под катом мы попытаемся построить более-менее осмысленную модель движения транспорта на дороге и, если повезет, постараемся смоделировать разницу в вождении водителя-человека и AI. Я разумеется отдаю себе отчет что этой проблемой профессионально занимаются целые организации и вообще очень умные люди, но тем интереснее. И вообще, ставьте себе нереальные цели.
И еще одно — я убежденный сторонник думанья головой, поэтому в этом посте компьютерного моделирования не будет, вообще совсем не будет, только хардкорный карандаш и бумага.
Для начала надо сказать что существует два похода — микроскопическая модель и статистическая. Первая рассматривает отдельно движение каждой машины в потоке как отдельный набор независимых переменных в одной огромной системе уравнений и, по понятным причинам, пользуется наибольшей популярностью у теоретиков. Вторая рассматривает всю совокупность как непрерывную среду где каждая отдельная машина описывается лишь вероятностно. Из чувства противоречия с этого второго случая и начнем.
Простейшая статистическая модель
Пусть имеется одна полоса с равномерно распределенными машинами с линейной плотностью ρ. Однако скорости у всех машин разные, будем считать что вероятность иметь скорость v описывается плотностью вероятности P(v,t) зависящей естественно от времени и равной в момент t=0 некоторой известной функции P(v,0). Можно без ограничения общности считать что вероятность P(v,t) определена на интервале от нуля до (да простят меня дорожные полиции всех стран) бесконечности. Определены также понятия нормировки и средней (групповой) скорости:
(1.1)
За время dt каждая имеющая скорость v проходит расстояние vdt и может как "исчезнуть" догнав более медленную и потеряв скорость, так и "увеличить массу", будучи догнанной более быстрой. Легко сообразить что за интервал времени dt вероятность машине со скоростью v догнать более медленную машину со скоростью u (и затормозиться) будет P(u,t)(v-u)dtdu и симметричноe выражение для вероятности быть догнанной более быстрой машиной (и затормозить ее). Таким образом изменение плотности вероятности со временем:
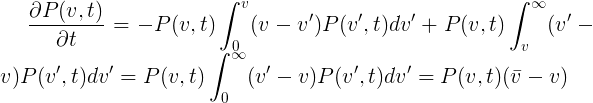(1.2)
Немного подумав достаточно легко понять что решение должно иметь вид A(v)B(t)exp(-ρvt) и отсюда полное решение:
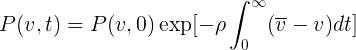(1.3)
Уравнение получилось изящное, но незамкнутое, поскольку средняя скорость сама зависит от времени. Однако нас не интересуют детали изменения плотности вероятности P(v,t) со временем, тем более что они зависят от произвольной начальной функции P(v,0), поэтому мы можем воспользоваться (1.1) чтобы замкнуть уравнение относительно ̅v
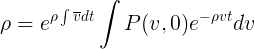и отсюда 
(1.4)
вот с этим уравнением уже можно работать, давайте рассмотрим пару частных случаев для иллюстрации.
Пусть изначально все машины движутся строго с одной скоростью:
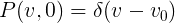отсюда
как и должно быть.
Пусть теперь изначально скорость распределена равномерно в некотором интервале:
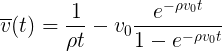
При этом средняя скорость падает как 1/t a среднее пройденное расстояние растет логарифмически:
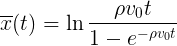— и это хорошая новость для тех кто читает этот пост стоя в пробке — до места вы все таки доберетесь, правда за экспоненциальное время.
Тут есть однако одно кажущееся противоречие — если в потоке присутствуют машины со сколь угодно малой скоростью, как может среднее пройденное расстояние увеличиваться со временем? Ответ в том что число машин со строго нулевой скоростью тоже равно нулю. Если мы возьмем начальное распределение в виде:
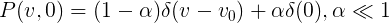
То есть почти все машины движутся с одинаковой скоростью, а некоторая очень малая часть просто стоит, то групповая скорость будет падать экспоненциально
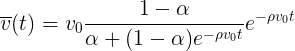
И среднее пройденное расстояние стремится к фиксированному пределу.
Таким образом мы потратили пару листов бумаги и показали что на однополосной дороге все рано или поздно уткнутся в хвост самой медленной машине и будут тащиться с ее скоростью — блестящий результат. Попробуем теперь немного более реальный вариант.
Шаг навстречу реальности
Если вы читали внимательно, к этому месту у вас должно было возникнуть чувство законного недоумения — а где же пробки? С какой стати мы полагаем линейную плотность ρ константой не зависящей ни от времени ни от координаты? В конце концов пробка и есть по сути скопление машин. Все правильно, в рамках нашей текущей модели мы рассматриваем профиль движения усредненный по очень большому интервалу, настолько большому что усредненная по нему плотность постоянна. Внутри него машины сбиваются в колонны между которыми совершенно пустые промежутки, но в характерном масштабе нашей модели все это несущественно. Характерный размер неоднородности, колонны или промежутка, растет со временем и вот, когда он наконец сравняется с характерным масштабом, пробка… могла бы возникнуть, но не возникает, потому что модель больше неприменима. Надо искать более детализированную модель. Обратите также внимание, что для отдельной машины движущейся в потоке нет никакого распределения по скоростям P(v,t) с которым мы работали раньше, существует только скорость v(x,t) и локальная плотность ρ(x,t). Вот с ней и поработаем.
Прежде всего, для плотности должно выполнятся уравнение непрерывности:
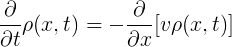(2.1)
абсолютно фундаментальный закон по сути означающий что сколько в трубу втекло, столько должно и вытечь. Заметьте что ρv — это просто число машин пересекающих сечение дороги за единицу времени.
Разумеется у этого уравнения существует бесконечное множество решений, например это может быть произвольная функция f(x-vt) описывающая движение произвольного профиля плотности с произвольной скоростью v. Если перейти в систему координат движущуюся вместе с машиной, то это выражение принимает еще более простой вид: ρv=const. Если скажем плотность меняется по закону ρf(x -vt) и впереди участок дороги с пониженной скоростью u, u < v, то там профиль плотности будет выглядеть как Pf(x-ut), где ρv=Pu. Такая модель подобна идеальному газу и описывает идеальное поведение трафика на дороге — при уменьшении скорости происходит пропорциональное увеличение плотности а число машин пересекающих сечение дороги в единицу времени постоянно (с точностью до флуктуаций f(x)), вы всегда можете рассчитать время за которое вы проедете определенное расстояние и оно не будет зависеть от других машин на дороге.
Так все-таки, где же пробки?
Модель идеального газа описывает состояние невзаимодействующих частиц, неидеальность начинается при учете взаимодействия. Аналогично получается и у нас — придется учитывать притормаживание когда машины оказываются слишком близко. Тормозной путь можно описать выражением v2/2a+vτ+d, где а — ускорение комфортного торможения оцененное (грубо) константой; τ — величина размерности времени и порядка времени реакции водителя; d — величина порядка длины автомобиля.
Пространственная плотность ρ должна быть обратной величиной. Получается? Нет, очевидно что в пределе больших скоростей плотность должна падать как 1/v а не 1/v2, а у нас получилось что даже поток машин через сечение дороги ρv падает с ростом скорости. Ошибка в том что водители вовсе не держат интервал обратно пропорциональный тормозному пути, это было бы так если бы впереди идущая машина могла бы остановиться мгновенно — слишком сильное предположение, на самом деле она тормозит с тем же самым ускорением a. Тогда у нас исчезает квадратичный член и получается разумное выражение:
ρmax=1/(vτ+d) (2.2)
при увеличении плотности до 1/d (то есть бампер в бампер) машины могут только стоять, а при росте скорости поток стремится к пределу: ρv=1/τ. Это выражение для предельной плотности при данной скорости, если автомобили сойдутся еще теснее, они начнут притормаживать. Может быть я слишком подробно на этом остановился, но хотелось показать как правильно заложенная модель начинает корректировать сама себя, через рассмотрение частных и предельных случаев выявляет ошибки.
Пусть по дороге движется колонна машин со одинаковыми скоростью v и плотностью ρ. Если эта колонна вьезжает на участок с пониженной скоростью u<v, то плотность машин увеличивается, как мы уже видели раньше, ρ*=ρv/u.
Однако, если плотность приближается к критической, может оказаться что новый участок дороги неспособен пропустить такой поток (максимальный поток машин через сечение дороги νmax(u)=uρmax(u)=u/(uτ+d) и монотонно уменьшается с уменьшением скорости)
ρ*=ρv/u > ρmax=1/(uτ+d).
Теперь в игру вступает уравнение (2.1) описывающее изменение скорости и профиля плотности, которое однако имеет бесконечное множество решений, включая нестационарные и колебательные. Давайте для оценки сверху возьмем идеальный случай оптимизирующий пропускную способность дороги, для этого каждую машину должен вести всеведущий демон Максвелла, но тем не менее. Тогда каждая машина будет притормаживать заранее в точно угаданный момент до мистически угаданной скорости u, примерно вот так:
Более того, граница торможения будет двигаться влево с легко вычисляемой скоростью:
[ρv-u/(uτ+d)]/[1/(uτ+d)-ρ]=[ν-νmax(u)]/[ρmax(u)-ρ] (2.3)
А что происходит на переднем фронте? Предположим что ограничение на скорость в некоторый момент исчезло, тогда фронт начнет испаряться — машины начнут ускоряться до начальной скорости v и фронт начнет тоже двигаться влево. Однако скорость испарения заведомо меньше скорости торможения; главным образом потому что водитель тормозит сразу же как только заметит стоп-сигналы впереди идущего, а для разгона ему нужно оценивать расстояние до впереди идущей машины и ее скорость. Оценить скорость испарения фронта достаточно трудно без привлечения эмпирических соображений, однако мы можем предположить что она может быть как больше, так и меньше скорости левой границы (2.3), которая в свою очередь зависит от ограничения скорости u. И, если она окажется меньше, то мы получаем что-то типа солитона на дороге — устойчивое образование, возникающее при случайном кратком торможении одной из машин и существующее конечное время. Важно добавить, что для возникновения такого солитона уже необязательно реального ограничения скорости, достаточно если одна из машин спонтанно замедлится на время больше τ до скорости меньше некоторой критической.
До собственно пробок остался один маленький шаг, достаточно заметить что образовавшийся солитон нестабилен, его плотность равна критической (2.2) и любое случайное достаточно сильное торможение одной из машин в колонне вызовет новый аналогичный процесс и образование нового уплотнения с еще меньшей скоростью. При достаточно большом времени жизни такого образования этот сценарий будет повторяться и лавинно накладываться один на другой вплоть до достижения разреженного участка на дороге или полной остановки машин в конце колонны, что мы собственно и наблюдаем в реальной жизни.
Сейчас можно было бы привлечь теорию вероятностей и прикинуть длину получившегося солитона (которая определяется флуктуациями плотности трафика), а так же время его жизни и вероятность возникновения еще больших уплотнений и шансы полной остановки движения, так же как и среднее уменьшение пропускной способности дороги. Короче, основываясь на этой простой модели возможно построить полное вероятностное описание дорожного трафика. Однако я подозреваю что давно исчерпал лимит на количество формул в посте, кроме того, потребовалось бы привлечение каких то эмпирических и/или количественных данных, чего я старался избегать всеми силами. Лично я уже достиг понимания как случаются пробки и получил от этого некоторое удовольствие. Кроме того я понял какая злая сила вырвала полчаса из моей жизни, и жить мне сразу стало лучше и веселее.
А как же роботы?
А с ними все просто, поскольку я не делал никаких человеко-специфических предположений, базовая модель верна и для них. То есть если заставить робомобили ехать по дороге на пределе ее пропускной способности, в потоке движения могут возникать спонтанные возмущения приводящие к замедлению вплоть до полной остановки. Однако вероятность таких возмущений можно постараться существенно понизить.
- Во-первых, в потоке состоящем исключительно из роботов гораздо реже возникают спонтанные флуктуации, роботы не чихают за рулем, не роняют зажженную сигарету, не отвлекаются на болтовню пассажиров и субьективных причин притормаживать у них практически нет. Однако обьективные причины (скользкий участок дороги например) все-таки остаются.
- Во-вторых, теоретически время реакции τ робота намного меньше, в пределе стремится к нулю. Однако я боюсь что разработчики робомобилей перестраховываясь искусственно его завышают в алгоритмах вождения. Со временем этот резерв тоже будет задействован.
- В-третьих, роботам чужды эмоции, в частности нетерпение, зависть и жадность. Это позволяет им держать дистанцию чуть-чуть больше минимально необходимой, в результате линейно чуть-чуть снижается пропускная способность, однако вероятность возникновения пробок падает нелинейно во много раз. Однако для этого необходимо чтобы на дороге робомобили как минимум преобладали.
- В-четвертых, и это самое существенное что отличает их от человека — роботы гораздо ближе к демонам Максвелла. В частности, если позволить им обмениваться информацией на дороге, можно создать виртуальный распределенный ИИ управляющий движением на каждом участке. Как простой пример — колонна из фур может очевидно выиграть если каждая будет знать скорость первой в колонне фуры в каждый момент. Еще один — если становится известно что где-то впереди (может быть достаточно далеко) начинается уплотнение, машины могут заранее увеличить интервал и таким образом блокировать распространение пробки. Ну и наконец, разгонное время можно кардинально уменьшить если машина получает сигнал об ускорении от впереди идущей, это позволило бы резко сократить время жизни солитона и предотвратить лавинный эффект.
- Ну и наконец для тех кто проектирует и строит дороги — не забывайте что у каждой дороги с ограничением скорости vmax есть максимальная пропускная способность порядка vmax/(τvmax+d) и, если ожидается увеличение потока (город растет) на каком-то участке до этой величины, хорошо бы заранее предусмотреть расширение дороги или увеличение максимальной скорости. Ну это уже из области абсолютных фантазий конечно.
Я не знаю какие модели разрабатываются сейчас производителями робомобилей, и вообще, готовятся ли они морально к тому времени когда они будут преобладать на дорогах; но мне кажется что уже пора. Локальные алгоритмы вождения пора дополнять и расширять до кооперативных и тогда мы будем меньше тратить времени на стояние в пробках, а значит и мир станет немножко лучше.
PS: Изначально я планировал этот пост на Гиктаймс, но с удивлением обнаружил отсутствие подходящих хабов. На мой взгляд, правильным сочетанием было бы Математика+Занимательные задачи+Транспорт будущего, однако оказалось что первые два присутствуют только на Хабре, причем в разделе Разработка. Ну и ладно, пишу туда где хабы соответствуют.