Сразу озвучу задачку, чтобы не было предвкушения, будто тут будет показан какой-то крутой новый метод шифрования.
Нужно доказать, что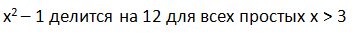
Статья ориентирована на студентов, заинтересованных граждан и просто зевак. У нас защита информации была на пятом курсе в институте. На лекциях по защите информации было много историй о нелегкой судьбе русских программистов в шальные девяностые: как им платили за работу пельменями, которые делались на цокольном этаже предприятия, где они работали, как делается самогон и т.п. А оставшееся время лекции посвящалось собственно аспектам защиты информации. На лекциях давалось очень много теории по темам, хоть как-то связанным с алгоритмами шифрования. На экзамене в каждом билете было пара вопросов по теории и одна задачка.
За день до нашего экзамена ребята с параллельной группы скинули одну задачку(описана в начале статьи), решить которую не смогли. Сидела я на работе, думала, как ее решить, около часа. Какие идеи и первые мысли по решению были у меня в голове на тот момент, я не скажу, уже несколько лет прошло. Кстати мне на экзамене попалась задачка такого же типа. Ниже покажу доказательство двух типовых задачек. Если вы знаете, как доказать по-другому, отпишитесь в комментариях.
Итак, приступим. Доказательство построено с использованием теоремы Эйлера.
Еще раз повторю задание. Нужно доказать, что делится на 12 для всех простых x > 3.
делится на 12 для всех простых x > 3.
x и 12 — взаимно простые, тогда по т.Эйлера, делится на 12, т.е. остаток от деления равен 0 (в теореме единица перенесена в правую часть равенства, сделаем так же):
делится на 12, т.е. остаток от деления равен 0 (в теореме единица перенесена в правую часть равенства, сделаем так же):

Для числа 12 существует четыре меньших него и взаимно простых с ним чисел (1, 5, 7, 11), поэтому функция Эйлера принимает значение четыре:
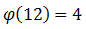

Перенесем единицу из правой части равенства влево и воспользуемся формулой из школы, разложим на множители разность квадратов:
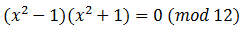
Сокращаем на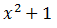 :
:

Что и требовалось доказать.
А теперь вот вам еще одна типовая задачка, которая попалась мне на экзамене. Когда решение было показано преподу, он почему-то был удивлен, поскольку, как он потом сказал, было бы достаточно просто посчитать в лоб, возвести в степень и показать, что одно число делится на другое. А решение, которое я ему показала, он видит впервые. Вот всегда думаешь, что для доказательства нужно применить теоремы, следствия, аксиомы, а оказывается «можно было просто в лоб посчитать».
Доказать, что число делится на 105.
делится на 105.
Если число делится нацело, то остаток 0. Числа 73 и 105 – взаимно простые => по т. Эйлера:
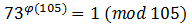
Вычисляем функцию Эйлера. Поскольку перебирать все числа меньше 105 и искать взаимно простые со 105 долго, разложим 105 на множители и найдем функцию Эйлера для каждого из них, а после просто перемножим:
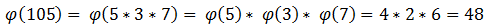

Переносим единицу влево и раскладываем на множители:

Сокращаем на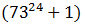 :
:
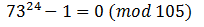
Разложим на множители и сократим еще раз:
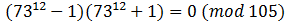

Остаток от деления на 105 — ноль, деление нацело. Ч.т.д.
на 105 — ноль, деление нацело. Ч.т.д.
Возможно, кому-то пригодится это решение, но, надеюсь, что у вас на ЗИ будет что-то поинтереснее.
Нужно доказать, что
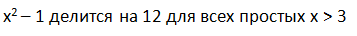
Статья ориентирована на студентов, заинтересованных граждан и просто зевак. У нас защита информации была на пятом курсе в институте. На лекциях по защите информации было много историй о нелегкой судьбе русских программистов в шальные девяностые: как им платили за работу пельменями, которые делались на цокольном этаже предприятия, где они работали, как делается самогон и т.п. А оставшееся время лекции посвящалось собственно аспектам защиты информации. На лекциях давалось очень много теории по темам, хоть как-то связанным с алгоритмами шифрования. На экзамене в каждом билете было пара вопросов по теории и одна задачка.
За день до нашего экзамена ребята с параллельной группы скинули одну задачку(описана в начале статьи), решить которую не смогли. Сидела я на работе, думала, как ее решить, около часа. Какие идеи и первые мысли по решению были у меня в голове на тот момент, я не скажу, уже несколько лет прошло. Кстати мне на экзамене попалась задачка такого же типа. Ниже покажу доказательство двух типовых задачек. Если вы знаете, как доказать по-другому, отпишитесь в комментариях.
Итак, приступим. Доказательство построено с использованием теоремы Эйлера.
Еще раз повторю задание. Нужно доказать, что
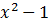 делится на 12 для всех простых x > 3.
делится на 12 для всех простых x > 3.x и 12 — взаимно простые, тогда по т.Эйлера,
 делится на 12, т.е. остаток от деления равен 0 (в теореме единица перенесена в правую часть равенства, сделаем так же):
делится на 12, т.е. остаток от деления равен 0 (в теореме единица перенесена в правую часть равенства, сделаем так же):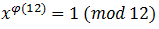
Для числа 12 существует четыре меньших него и взаимно простых с ним чисел (1, 5, 7, 11), поэтому функция Эйлера принимает значение четыре:
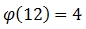

Перенесем единицу из правой части равенства влево и воспользуемся формулой из школы, разложим на множители разность квадратов:
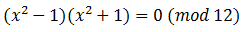
Сокращаем на
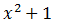 :
: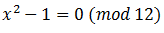
Что и требовалось доказать.
А теперь вот вам еще одна типовая задачка, которая попалась мне на экзамене. Когда решение было показано преподу, он почему-то был удивлен, поскольку, как он потом сказал, было бы достаточно просто посчитать в лоб, возвести в степень и показать, что одно число делится на другое. А решение, которое я ему показала, он видит впервые. Вот всегда думаешь, что для доказательства нужно применить теоремы, следствия, аксиомы, а оказывается «можно было просто в лоб посчитать».
Доказать, что число
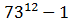 делится на 105.
делится на 105.Если число делится нацело, то остаток 0. Числа 73 и 105 – взаимно простые => по т. Эйлера:

Вычисляем функцию Эйлера. Поскольку перебирать все числа меньше 105 и искать взаимно простые со 105 долго, разложим 105 на множители и найдем функцию Эйлера для каждого из них, а после просто перемножим:
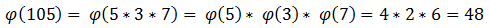
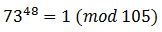
Переносим единицу влево и раскладываем на множители:
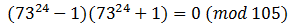
Сокращаем на
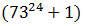 :
: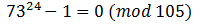
Разложим на множители и сократим еще раз:
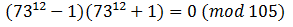
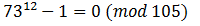
Остаток от деления
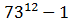 на 105 — ноль, деление нацело. Ч.т.д.
на 105 — ноль, деление нацело. Ч.т.д.Возможно, кому-то пригодится это решение, но, надеюсь, что у вас на ЗИ будет что-то поинтереснее.