Важным условием корректности построенного эскиза является непротиворечивость наложенных ограничений. Если наложено меньше ограничений, чем требуется, некоторые параметры не могут быть однозначно определены, поэтому могут изменяться в некотором диапазоне значений. В таких случаях говорят, что чертеж имеет степени свободы (Degrees Of Freedom; DOF). Анализ степеней свободы позволяет инженеру-конструктору накладывать только необходимое и достаточное количество ограничений, не позволяя системе уравнений быть переопределенной (overconstrained), и не позволяя оставить какую-либо степень свободы без наложенных ограничений.
Часть 1: Введение
Часть 2: Эскиз
Часть 3: Степени свободы и уравнения ограничений
Часть 4: «Неисповедимы пути Решателя» или «Червоточины Ньютона»

Переопределение системы уравнений опасно тем, что решение такой системы может быть найдено, и это не будет вызывать видимых проблем до тех пор, пока инженер не изменит значение одного из конфликтующих ограничений. В таком случае возникает противоречие между ограничениями, и система уравнений становится несовместной (inconsistent), что означает, что она не имеет решений. Без анализа степеней свободы будет сложно найти конфликтующие ограничения, так как чертежи могут содержать сотни ограничений.
Когда количество наложенных ограничений меньше, чем требуется для того, чтобы определить значения всех неизвестных параметров, система называется недоопределенной (underconstraint). При проектировании деталей такой случай опасен и может приводить к проблемам. Например, инженер-конструктор может изменить значение одного ограничения, а затем вернуть это значение обратно. В случае полностью определенного чертежа, эти действия сработают как изменение-отмена, но в случае неполного ограничения, значения свободных параметров могут измениться.
Уравнения (Equations)
Чтобы определить взаимосвязи между параметрами чертежа, необходимо задать их в виде уравнений. Давайте посмотрим, как выглядят основные уравнения, через которые задается большинство ограничений.
POINTS_COINCIDENT
Ограничение совпадения двух точек: просто уравниваем их координаты. Такое уравнение можно решать методом подстановки, исключив из рассмотрения два параметра одной из точек, заменив их упоминания на параметры совпадающей точки, а после решения всей системы сделать обратное замещение. Это ограничение снимает 2 степени свободы.

HORIZONTAL/VERTICAL
Ограничения горизонтальность/вертикальность: здесь достаточно уравнять одну из координат точек. Ограничение снимает одну степень свободы.

PT_PT_DISTANCE
Ограничение расстояния между точками: здесь используется теорема Пифагора. Ограничение снимает одну степень свободы.
 !
!
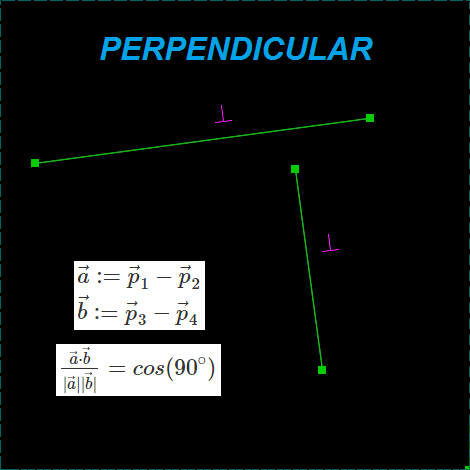
PERPENDICULAR
Перпендикулярность прямых: используется свойство скалярного произведения быть пропорциональным косинусу угла между векторами. Ограничение снимает одну степень свободы.
ANGLE
Ограничение угла между прямыми: используется все то же уравнение. Ограничение снимает одну степень свободы.

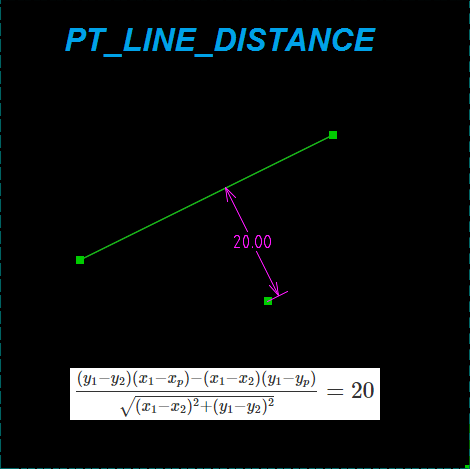
PT_LINE_DISTANCE
Ограничение расстояния от точки до линии записывается через псевдоскалярное (косое) произведение и используется его свойство:
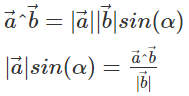
где 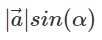 и есть искомая высота.
и есть искомая высота.
Ограничение снимает одну степень свободы.
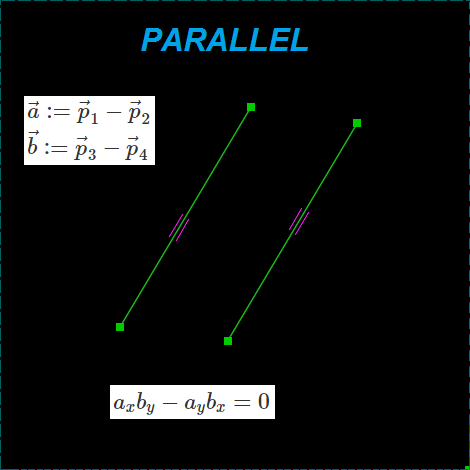
PARALLEL
Ограничение параллельности тоже основано на псевдоскалярном (косом) произведении. Здесь используется тот факт, что sin(0) = 0. По-честному, нужно было бы поделить левую часть уравнения на произведение модулей векторов, но исторически в SolveSpace уравнение записано именно так. Так как к нулевому результату косого произведения приводит и равенство нулю длин векторов, отрезки все время стремятся уменьшиться. Это не сильно мешает, если длину векторов ограничить.
Заключение
Все остальные двумерные ограничения построены на основе вышеизложенных уравнений. В следующей части мы познакомимся с методом численного решения систем уравнений, а именно с методом Ньютона.
Часть 1: Введение
Часть 2: Эскиз
Часть 3: Степени свободы и уравнения ограничений
Часть 4: «Неисповедимы пути Решателя» или «Червоточины Ньютона»