 Ранее в своей статье я рассказывал о том, как устроены фазовые лазерные дальномеры. Теперь пришло время разобраться с тем, как работают бытовые лазерные рулетки. Разобраться — это не просто заглянуть, что же там внутри, а полностью восстановить всю схему и написать собственную программу для микроконтроллера.
Ранее в своей статье я рассказывал о том, как устроены фазовые лазерные дальномеры. Теперь пришло время разобраться с тем, как работают бытовые лазерные рулетки. Разобраться — это не просто заглянуть, что же там внутри, а полностью восстановить всю схему и написать собственную программу для микроконтроллера.Принцип работы лазерных рулеток
Большинство лазерных рулеток используют фазовый, а не импульсный (времяпролетный, TOF) метод измерения расстояния.
Для целостности этой статьи процитирую часть теории из своей предыдущей статьи:
В фазовом методе, в отличие от импульсного, лазер работает постоянно, но его излучение амплитудно модулируется сигналом определенной частоты (обычно это частоты меньше 500МГц). Отмечу, что длина волны лазера при этом остается неизменной (она находится в пределах 500 — 1100 нм).
Отраженное от объекта излучение принимается фотоприемником, и его фаза сравнивается с фазой опорного сигнала — от лазера. Наличие задержки при распространении волны создает сдвиг фаз, который и измеряется дальномером.
Расстояние определяется по формуле:
Где с — скорость света, f — частота модуляции лазера, фи — фазовый сдвиг.
Эта формула справедлива только в том случае, если расстояние до объекта меньше половины длины волны модулирующего сигнала, которая равна с / 2f.
Если частота модуляции равна 10 МГц, то измеряемое расстояние может доходить до 15 метров, и при изменении расстояния от 0 до 15 метров разность фаз будет меняться от 0 до 360 градусов. Изменение сдвига фаз на 1 градус в таком случае соответствует перемещению объекта примерно на 4 см.
При превышении этого расстояния возникает неоднозначность— невозможно определить, сколько периодов волны укладывается в измеряемом расстоянии. Для разрешения неоднозначности частоту модуляции лазера переключают, после чего решают получившуюся систему уравнений.
Самый простой случай — использование двух частот, на низкой приблизительно определяют расстояние до объекта (но максимальное расстояние все равно ограничено), на высокой определяют расстояние с нужной точностью — при одинаковой точности измерения фазового сдвига, при использовании высокой частоты точность измерения расстояния будет заметно выше.
Так как существуют относительно простые способы измерять фазовый сдвиг с высокой точностью, то точность измерения расстояния в таких дальномерах может доходить до 0.5 мм. Именно фазовый принцип используется в дальномерах, требующих большой точности измерения — геодезических дальномерах, лазерных рулетках, сканирующих дальномерах, устанавливаемых на роботах.
Однако у метода есть и недостатки — мощность излучения постоянно работающего лазера заметно меньше, чем у импульсного лазера, что не позволяет использовать фазовые дальномеры для измерения больших расстояний. Кроме того, измерение фазы с нужной точностью может занимать определенное время, что ограничивает быстродействие прибора.
Как я уже упоминал выше, для повышения точности нужно повышать частоту модуляции излучения лазера. Однако измерить разность фаз двух высокочастотных сигналов достаточно сложно. Поэтому в фазовых дальномерах часто применяют гетеродинное преобразование сигналов. Структурная схема такого дальномера показана ниже. Рассматриваемая мной лазерная рулетка устроена именно так.
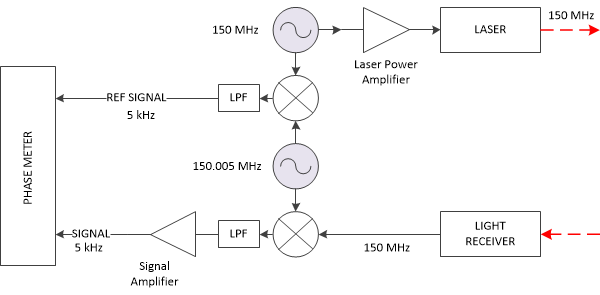
В состав дальномера входят два высокочастотных генератора, формирующие два сигнала, близких по частоте. Сигнал с одного из них подается на лазер, сигнал от другого (гетеродина) перемножается с сигналом, принятым фотоприемником. Получившийся сигнал подается на фильтр, пропускающий только низкие частоты (LPF), так что на выходе фильтра остается только сигнал разностной частоты. Этот сигнал имеет очень маленькую амплитуду, и его приходится усиливать, прежде чем подавать на микроконтроллер. Стоит заметить, что сделать низкочастотный усилитель с большим коэффициентом усиления намного проще, чем высокочастотный, что также является преимуществом гетеродинной схемы.
Поскольку в фазовом дальномере измеряется именно разность фаз сигналов, то в конструкции нужен еще один сигнал — опорный. Его получают перемножением сигналов от обоих генераторов. Оба получившихся низкочастотных сигнала обрабатываются микроконтроллером дальномера, который вычисляет разность фаз между ними.
Отдельно стоит упомянуть, что в большинстве лазерных дальномеров в качестве фотоприемников используются лавинные фотодиоды (APD). Они обладают собственным внутренним усилением сигнала, что уменьшает требования к усилительным узлам дальномера. Коэффициент усиления таких фотодиодов нелинейно зависит от питающего напряжения. Таким образом, если модулировать напряжение питания APD сигналом гетеродина, то смешивание (перемножение) сигналов происходит прямо в самом фотодиоде. Это позволяет упростить конструкцию дальномера, и уменьшить влияние шумов.
В тоже время, у лавинных фотодиодов много недостатков. К ним можно отнести:
- Напряжение питания должно быть достаточно высоким — сотня вольт и выше.
- Сильная зависимость параметров от температуры.
- Достаточно высокая стоимость (по сравнению с другими фотодиодами).
Реверс-инжиниринг лазерной рулетки
 В качестве подопытного образца я использовал набор «50M DIY Rangefinder», найденный на просторах Aliexpress (справа приведена фотография включенной рулетки). Насколько я понял, этот набор — внутренности лазерной рулетки «X-40» (сейчас ее можно найти в продаже за 20$). Этот набор я выбрал только потому, что на его фотографиях было видно электронику устройства. По имеющейся у меня информации, схемотехника этой рулетки очень близка к схемотехнике рулетки U-NIT UT390B+, и другим китайским лазерным рулеткам и модулям лазерных дальномеров.
В качестве подопытного образца я использовал набор «50M DIY Rangefinder», найденный на просторах Aliexpress (справа приведена фотография включенной рулетки). Насколько я понял, этот набор — внутренности лазерной рулетки «X-40» (сейчас ее можно найти в продаже за 20$). Этот набор я выбрал только потому, что на его фотографиях было видно электронику устройства. По имеющейся у меня информации, схемотехника этой рулетки очень близка к схемотехнике рулетки U-NIT UT390B+, и другим китайским лазерным рулеткам и модулям лазерных дальномеров.Во время испытаний я смог проверить работу рулетки только на расстоянии в 10 м. Работала она при этом с большим трудом, время измерения было больше 5 секунд. Подозреваю, что даже расстояние в 20 метров она измерить бы уже не смогла, не говоря о заявленных производителем 50 м.
Что же представляет из себя конструкция такой рулетки?

Как видно из фотографий, она достаточно проста. Конструктивно рулетка состоит из блока лазерного дальномера, индикатора и платы с кнопками. Очевидно, что самое интересное — это блок дальномера. Вот так он выглядит вблизи:

С верхней стороны платы расположены две основные микросхемы дальномера — микроконтроллер STM32F100C8T6 и сдвоенный PLL генератор Si5351. Эта микросхема способна формировать два сигнала с частотами до 200 МГц. Именно она формирует сигнал для модуляции лазера и сигнал гетеродина. Также на этой стороне платы расположен смеситель и фильтр опорного (REF) сигнала и часть деталей узла высоковольтного источника напряжения для APD (вверху фотографии).
Так выглядит нижняя сторона блока дальномера:

Из фотографии может быть не понятно, но на самом деле здесь видно две печатные платы — вторая очень маленькая и закреплена вертикально. На этой фотографии хорошо видно выводы лазерного диода, маленький динамик (он постоянно пищал при работе, так что позже я его выпаял). Кроме того, здесь находятся компоненты, формирующие питающие напряжения рулетки.
На маленькой платке расположен лавинный фотодиод со встроенным интерференционным светофильтром и усилитель принятого сигнала. Вот так выглядит эта плата сбоку:

На фотографии справа показан вид лавинного фотодиода через линзу-объектив рулетки.
Следующий этап — восстановление схемы рулетки. Плата довольно маленькая и не очень сложная, хотя и многослойная, так что процесс восстановления схемы занял не очень много времени.
Фото платы с подписанными компонентами:



В одном из китайских интернет-магазинов мне удалось найти картинку с изображением печатной платы модуля лазерного дальномера (версия 511F), которая была очень близка по конструкции с моей платой (версия 512A). Разрешение картинки довольно низкое, зато на ней видно расположение проводников и переходных отверстий под микросхемами. В дальнейшем я подписал на ней номера компонентов и выделил проводники:
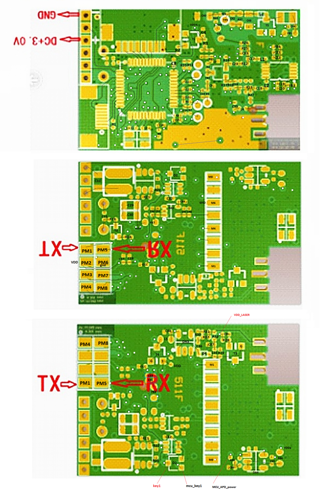
К сожалению, по маркировке части SMD компонентов не удалось определить их названия. Номиналы большинства конденсаторов нельзя определить без выпаивания их из платы. Номиналы резисторов я измерял мультиметром, так что они могут быть определены неточно.
В результате исследования у меня получилась вот такая структурная схема рулетки:

Электрическую схему я разбил на несколько листов:

Схема 1. Микроконтроллер, узел питания и некоторое простые цепи.
Здесь все достаточно просто — тут показаны микроконтроллер STM32, некоторые элементы его обвязки, динамик, клавиатура, некоторые ФНЧ фильтры. Здесь же показан повышающий DC-DC преобразователь напряжения (микросхема DA1), формирующий напряжение питания рулетки.
Рулетка рассчитана на работу от 2 батареек, напряжение которых может меняться в процессе работы. Указанный преобразователь формирует из входного напряжения VBAT постоянное напряжение 3.5 В (несколько необычное значение). Для включения и выключения питания рулетки используется узел, собранный на транзисторной сборке DA2. При нажатии кнопки S1 он включает DC-DC, после чего микроконтроллер сигналом по линии «MCU_power» начинает удерживать DC-DC включенным.
Во время одного из измерений я случайно сжег микросхему этого DC-DC преобразователя (щуп мультиметра соскочил, и замкнул ее ножки). Так как я не смог определить название микросхемы, мне пришлось выпаять ее, и подавать на рулетку напряжение 3.5 В от внешнего источника напряжения.
Снизу на краю платы есть 8 прямоугольных площадок, которые могут использоваться как отладочные или тестовые. Я отметил их на схеме «PMx». Из схемы видно, что все они подключены к выводам микроконтроллера. Среди них есть линии UART. Родная прошивка не ведет никакой активности на этих линиях, линия TX, судя по осциллографу, сконфигурирована на вход.
Также на краю платы есть 6 отверстий-контактов. На схеме они отмечены «Px». На них выведены линии питания рулетки и линии программирования STM32.
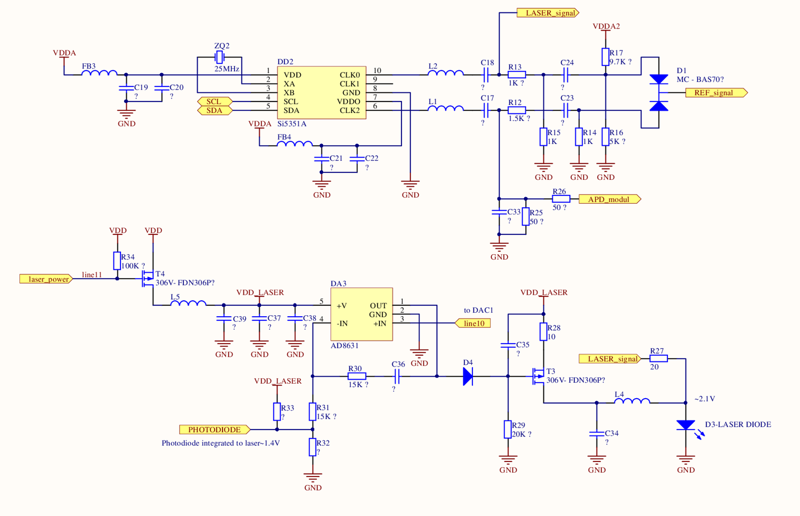
Схема 2. Узел PLL генератора, и узел управления лазерным диодом.
Микросхема PLL генератора Si5351 формирует прямоугольный сигнал, поэтому, чтобы убрать лишние гармоники, сигналы с выхода PLL подаются на два одинаковых полосовых фильтра. Тут же показан смеситель сигналов, собранный на диоде D1 — сигнал с него используется в качестве опорного при измерении разности фаз.
Как можно видеть из схемы, один из сигналов c PLL («LASER_signal») выводится на лазерный диод D3 без каких-либо преобразований. С другой стороны, яркость лазера (которая определяется величиной тока, текущим через него) стабилизируется при помощи аналогового узла, собранного на микросхеме DA3 и окружающих ее компонентах. Реальный уровень яркости лазера этот узел получает от встроенного в лазер фотодиода (он не показан на схеме). При помощи линии «laser_power» микроконтроллер может полностью отключить лазер, а при помощи линии «line10», соединенной с ЦАП микроконтроллера — регулировать яркость лазера. Исследование осциллографом показало, что рулетка постоянно удерживает на этой линии значение 1.4 В, и оно не меняется ни при каких условиях.

Схема 3. Узел питания APD и усилитель сигнала с APD.
Слева здесь показан линейный источник напряжения, формирующий питающее напряжение для усилителя фотодиода (DA5). Эта микросхема формирует напряжение 3.3 В, так что напряжение на ее входе должно быть выше 3.3 В. Насколько я понимаю, именно это служит причиной того, что остальная часть схемы питается от 3.5 В.
Ниже показан повышающий DC-DC преобразователь, собранный на микросхеме DA4, формирующий высокое напряжение (> 80 В) для лавинного фотодиода. Микроконтроллер может изменять величину этого напряжения при помощи линии «MCU_APD_CTRL», соединенной с ЦАП контроллера. Название микросхемы DA4 мне не удалось установить, так что пришлось экспериментально определять, как зависит напряжение на APD от уровня управляющего сигнала. Эта зависимость получается какая-то странная, с ростом величины управляющего сигнала, выходное напряжение падает. В дальнейших экспериментах я использовал несколько константных значений ЦАП, для которых я знал соответствующие им выходные напряжения.
Справа на схеме 3 показана схема маленькой печатной платы. Линиями M1-M8 показаны контактные площадки, соединяющие обе платы. Диод D6 — это лавинный фотодиод (APD). Он никак не промаркирован, так что определить его название и характеристики невозможно. Могу лишь сказать, что он имеет корпус LCC3.
На катод APD по линии M8 подается высокое постоянное напряжение. Также можно видеть, что через конденсатор C41 по линии «APD_modul» к нему подмешивается высокочастотный сигнал от PLL. Таким образом, на APD смешиваются оптический сигнал и сигнал «APD_modul», имеющие разные частоты. В результате этого на выходе APD появляется низкочастотный сигнал, который выделяется полосовым фильтром (компоненты C55, R41, R42, R44, C58, C59).
Далее низкочастотный сигнал усиливается операционным усилителем DA6B (SGM8542). Сигнал с выхода DA6B передается на АЦП микроконтроллера по линии M2. Также этот сигнал дополнительно усиливается транзистором T6 и передается на микроконтроллер по линии M1.
Такое ступенчатое усиление нужно из-за того, что уровень входного сигнала меняется в очень широких пределах.
Кроме того, рядом с APD установлен терморезистор R58, позволяющий определить температуру APD. Как я уже говорил, параметры APD сильно зависят от температуры, и терморезистор нужен для программной компенсации этой зависимости. В процессе работы APD нагревается, и даже это изменяет его характеристики. К примеру, при комнатной температуре из-за собственного нагрева усиление фотодиода падает более чем в 2 раза.
В случае, когда уровня принимаемого сигнала не хватает, микроконтроллер повышает напряжение на APD, таким образом увеличивая усиление. Во время проверки работы рулетки с родной прошивкой я обнаружил, что там есть только два уровня выходного напряжения — 80 и 93 В. Однако в то время я не догадался, что эти уровни могу зависеть от температуры APD, и не проверил, меняются ли в рулетке какие-либо управляющие сигналы при нагреве.
На фотографиях платы видно, что на ней есть контрольные площадки. Я отметил их на схеме и плате: «TPx». Среди них можно выделить:
- TP3, TP4 — низкочастотный сигнал с усилителя фотодиода. Именно этот сигнал несет информацию о расстоянии до объекта. При помощи осциллографа можно увидеть, что сигнал имеет частоту 5 кГц, и содержит постоянную составляющую.
- TP1 — опорный сигнал. Также имеет частоту 5 кГц и содержит постоянную составляющую. Амплитуда этого сигнала довольно мала — около 100 мВ.
- TP5 — высокое напряжение питания лавинного фотодиода.
Программирование
Прежде чем пытаться сделать что-то с родной прошивкой контроллера, я решил снять логическим анализатором обмен между STM32 и PLL, который происходит по I2C шине. Для этого я припаял провода к подтягивающим резисторам шины:

Мне без проблем удалось перехватить обмен между упомянутыми микросхемами и декодировать данные в передаваемых посылках:

Анализ результатов показал, что контроллер всегда только записывает информацию в PLL, и ничего не считывает. При хорошем уровне сигнала один цикл измерений занимает около 0.4 секунд, при плохом уровне сигнала измерения идут значительно дольше.
Видно, что микроконтроллер передает в PLL достаточно крупные посылки с периодом около 5 мс.
Поскольку данных было много, для их анализа я написал специальную программу на Python. Программа определяла и подсчитывала посылки, определяла размер посылок, время между ними. Кроме того, программа выводила названия регистров PLL, в которые производится запись передаваемых байтов.
Как оказалось, каждые 5 мс STM32 полностью перезаписывает основные регистры PLL (длина пакета 51 байт), в результате чего PLL меняет обе частоты. Никакой инициализации PLL рулетка не проводит — то есть пакеты передаваемых данных несут полную конфигурацию PLL. При хорошем уровне сигнала цикл измерений состоит из 64 передач данных.
Далее я добавил в программу расчет частоты по данным, передаваемым в пакетах. Выяснилось, что в процессе измерений рулетка использует четыре частоты модуляции лазера:
- 162.0 MHz
- 189.0 MHz
- 192.75 MHz
- 193.5 MHz
Частота гетеродина (второй выход PLL) при этом всегда имеет частоту, на 5 кГц меньшую, чем частота модуляции лазера.
Судя по всему, 4 цикла переключения частот (по 5 мс каждый) позволяют обеспечить однократное определение расстояния. Таким образом, проведя 64 цикла, рулетка выполняет 16 измерений расстояния, после чего усредняет и фильтрует результаты, за счет чего повышается точность измерения.
Далее я приступил к написанию своей программы для микроконтроллера рулетки.
После подключения программатора к рулетке компьютер не обнаружил ее микроконтроллер. Насколько я понимаю, это значит, что в родной прошивке интерфейс SWD отключен программно. Эту проблему я обошел, подключив к рулетке линию программатора NRST и выбрав в настройках ST-LINK Utility режим «Connect under reset». После этого компьютер обнаружил контроллер, но, как и ожидалось, родная прошивка была защищена от чтения. Для того, чтобы записать в контроллер свою программу, Flash-память контроллера пришлось стереть.
Первым делом в своей программе я реализовал включение питания аналоговой части дальномера, включение лазера и установку его тока, включение напряжения питания APD. После того, как я убедился, что все напряжения в норме, можно было экспериментировать с PLL. Для теста я просто реализовал запись в PLL тех данных, которые я ранее получил с рулетки.
В результате после запуска своей программы я обнаружил, что на контрольных точках появился сигнал с частотой 5 кГц, амплитуда которого явно зависела от типа объекта, на которые светил лазер. Это значило, что вся аналоговая электроника работает правильно.
После этого я добавил в программу захват аналогового сигнала при помощи АЦП. Стоит отметить, что для измерения разности фаз сигналов микроконтроллер должен захватывать уровни основного и опорного сигналов одновременно или с постоянной задержкой. В STM32F100 последний вариант можно реализовать, используя режим сканирования АЦП. Данные от АЦП при этом логично захватывать в память при помощи DMA, а для того, чтобы данные захватывались с заданной частотой дискретизации, запуск преобразования АЦП должен производиться по сигналу от одного из таймеров.
В результате экспериментов я остановился на следующих параметрах захвата:
— Частота дискретизации АЦП — 50 кГц,
— Количество выборок — 250.
— Суммарное время захвата сигнала — 5 мс.
— Захваченные данные программа контроллера передает на ПК по UART.
Для обработки захваченных данных я написал на C# небольшую программу:
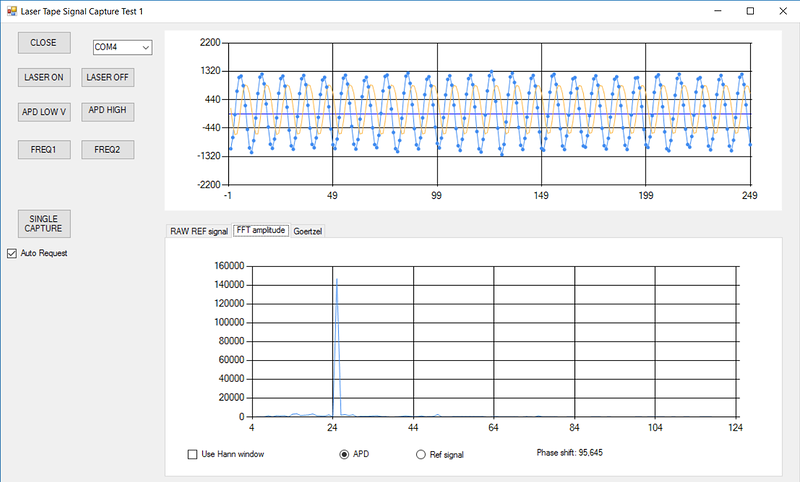
График синего цвета — принятый сигнал, график оранжевого цвета — опорный сигнал (его амплитуда на этом графике увеличена в 20 раз).
На графике снизу показан результат FFT преобразования принятого сигнала.
Используя FFT, можно определить фазу сигнала — нужно рассчитать фазовый спектр сигнала, и выбрать из него значение фазы в точке, соответствующей 5кГц. Отмечу, что я пробовал выводить фазовый спектр на экран, но он выглядит шумоподобным, так что я от этого отказался.
В то же время в действительности на микроконтроллер поступают два сигнала — основной и опорный. Это значит, что нужно вычислить при помощи FFT фазу каждого из сигналов на частоте 5 кГц, а затем вычесть из одного результата другой. Результат — искомая разность фаз, которая и используется для расчета расстояния. Моя программа выводит это значение под графиком спектра.
Очевидно, что использование FFT — не самый подходящий метод определения фазы сигнала на единственной частоте. Вместо его я решил использовать алгоритм Гёрцеля. Процитирую Википедию:
Алгоритм Гёрцеля (англ. Goertzel algorithm) — это специальная реализация дискретного преобразования Фурье (ДПФ) в форме рекурсивного фильтра.… В отличие от быстрого преобразования Фурье, вычисляющего все частотные компоненты ДПФ, алгоритм Гёрцеля позволяет эффективно вычислить значение одного частотного компонента.
Этот алгоритм очень прост в реализации. Как и FFT, он может возвращать комплексный результат, благодаря чему можно рассчитать фазу сигнала. В случае использования этого алгоритма также нужно рассчитать фазы основного и опорного сигналов, после чего вычислить их разность.
Эта же программа для ПК позволяет вычислять разность фаз и амплитуду сигнала при помощи алгоритма Герцеля. Результаты экспериментов показали, что при хорошем уровне сигнала точность измерения разности фаз может доходить до 0.4 градусов (СКЗ по 20 измерениям).
На следующем этапе я написал программу для микроконтроллера, которая сама рассчитывала разность фаз сигналов для трех разных частот модуляции (при помощи алгоритма Герцеля), и передавала результат на ПК. Почему использовались именно три частоты — я объясню позднее. За счет того, что расчеты производятся на самом микроконтроллере, нет необходимости передавать большой объем данных по UART, что значительно увеличивает скорость измерений.
Для ПК была написана программа, которая позволяла захватывать принимаемые данные и логировать их.
Именно на этом этапе я заметил сильное влияние температуры лавинного фотодиода на результаты измерения разности фаз. Кроме того, я заметил, что амплитуда принимаемого светового сигнала также влияет на результат. Кроме того, при изменении напряжения питания APD вышеуказанные зависимости явно изменяются.
Честно говоря, в процессе исследований я понял, что задача определения влияния сразу нескольких факторов (напряжения питания, амплитуды светового сигнала, температуры) на разность фаз достаточно сложна, и, в идеале, требует большого и длительного исследования. Для такого исследования нужна климатическая камера для имитации различных рабочих температур и набор светофильтров для исследования влияния уровня сигнала на результат. Нужно сделать специальный стенд, способный автоматически изменять уровень светового сигнала. Исследования осложняются тем, что при уменьшении температуры растет усиление APD, причем до такой степени, что APD входит в режим насыщения — сигнал на его выходе превращается из синусоидального в прямоугольный или вообще исчезает.
Такого оборудования у меня не было, так что пришлось ограничится более простыми средствами. Я проводил исследования работы дальномера только при двух рабочих напряжениях лавинного фотодиода (Uapd) в 82 В и 98 В. Все исследования шли при частоте модуляции лазера 160 МГц.
В своих исследованиях я считал, что изменения амплитуды светового сигнала и температуры независимо друг от друга влияют на результаты измерения разности фаз.
Для изменения амплитуды принимаемого светового сигнала я использовал специальный подвижный столик с прикрепленной заслонкой, которая могла перекрывать линзу-объектив фотодиода:

С изменением температуры все было сложней. В первую очередь, как я уже упоминал ранее, у APD был заметный эффект саморазогрева, который хорошо отслеживался термодатчиком. Для охлаждения рулетки я накрыл ее коробом из пенопласта с установленным в нем вентилятором, и установил сверху емкость с холодной водой. Кроме того, я пробовал охлаждать рулетку на балконе (там было около 10 °C). Судя по уровню сигнала с термодатчика, оба метода давали примерно одинаковую температуру APD. С нагревом все проще — я нагревал рулетку потоком горячего воздуха. Для этого я использовал резистор, прикрепленный к кулеру — так можно было регулировать температуру воздуха.
У меня не было никакой информации об установленном в рулетке терморезисторе, так что я нигде не пересчитывал результаты преобразования АЦП в градусы. При увеличении температуры уровень напряжения на АЦП падал.
В результате получились такие результаты:
- При увеличении Uapd (то есть с ростом усиления) заметно возрастает чувствительность APD к изменениям температуры и изменению уровня сигнала.
- При уменьшении амплитуды светового сигнала появляется небольшой сдвиг фазы — примерно +2 градуса при изменении амплитуды от максимальной до минимальной.
- При охлаждении APD появляется положительный сдвиг фазы.
Для напряжения 98 В получилась такая зависимость фазового сдвига от температуры (в единицах АЦП):
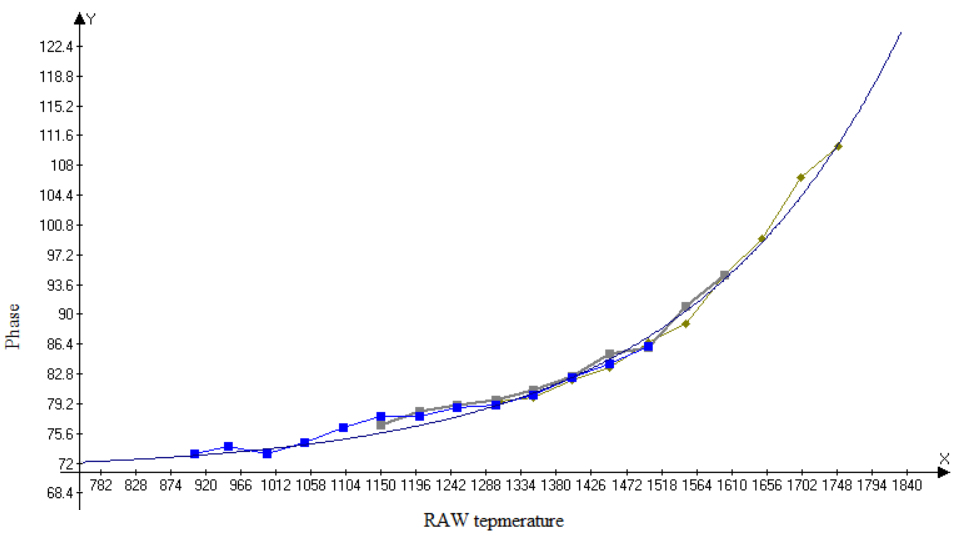
Можно видеть, что при изменении температуры (примерно от 15 до 40 градусов) разность фаз изменяется более чем на 30 градусов.
Для напряжения 82 В эта зависимость получилась практически линейной (по крайней мере, в том диапазоне температур, где я проводил измерения).
В результате, я получил два графика для двух Uapd, которые показывали связь между температурой и фазовым сдвигом. По этим графикам я определил две математические функции, которые использовал в микроконтроллере для коррекции значения разности фаз. Таким образом, я смог избавиться от влияния изменения внешних факторов на правильность измерений.
Следующий этап — определение расстояния до объекта по трем полученным разностям фаз. Для начала, я решил сделать это на ПК.
В чем тут проблема? Как я уже упоминал ранее, если частота модуляции достаточно высокая, то на определенном расстоянии от дальномера при попытке определить расстояние возникает неоднозначность. В таком случае для точного определения расстояния до объекта нужно знать не только разность фаз, но и число целых фаз сигнала (N), которые укладываются в этом расстоянии.
Расстояние в результате определяется формулой:
Из анализа работы заводской программы рулетки видно, что частоты модуляции лежат в диапазоне 160-195 МГц. Вполне вероятно, что схемотехника рулетки не позволит модулировать излучение лазера с меньшей частотой (я это не проверял). Это значит, что метод определения расстояния до объекта по разности фаз в рулетке должен быть сложнее, чем простое переключение между высокой и низкой частотами модуляции.
Стоит заметить, что из-за того, что частоты модуляции разные, то число целых фаз сигнала в одних случаях может иметь общее значение N, а в других — нет (N1, N2 ...).
Мне известны только два варианта решения этой задачи.
Первый вариант — простой перебор значений N и соответствующих им расстояний для каждой используемой частоты модуляции.
В ходе такого перебора ищутся такие значения N, которые дают наиболее совпадающие друг с другом расстояния (полного совпадения можно не получить из-за ошибок при измерении разности фаз).
Недостаток этого метода — он требует производить много операций и достаточно чувствителен к ошибками измерения фаз.
Второй вариант — использование эффекта биений сигналов, имеющих близкие частоты модуляции.
Пусть в дальномере используются две частоты модуляции сигнала с длинами волн
Можно предположить, что на дистанции до объекта количество целых периодов N1 и N2 равны между собой и равны некому значению N.
В таком случае получается такая система уравнений:
Из нее можно вывести значение N:
Получив значение N, можно вычислить расстояние до объекта.
Максимальное расстояние, на котором выполняется вышеупомянутое утверждение, определяется формулой:
Из этой формулы видно, что чем ближе друг к другу длины волн сигналов, тем больше максимальное расстояние.
В то же время, даже на указанной дистанции в некоторых случаях это утверждение (N1=N2) выполнятся не будет.
Приведу простой пример.
Пусть
В таком случае
Но если при этом путь, который проходит свет, равен 1.53м, то получается что для первой длины волны N1 = 0, а для второй N2 = 1.
В результате расчета величина N получается отрицательной.
Бороться c этим эффектом можно, используя знание, что
В таком случае можно модифицировать систему уравнений:
Используя эту систему уравнений, можно найти N1.
Применение этого метода имеет определенную особенность — чем ближе друг друг к другу длины волн сигналов модуляции, тем больше влияние ошибок измерения разности фаз на результат. Из-за наличия таких ошибок значение N может вычисляться недостаточно точно, но, по крайней мере, оно оказывается близким к реальной величине.
При определении реального расстояния до объекта приходится производить калибровку нуля. Делается она достаточно просто — на определенном расстоянии от рулетки, которое будет принято за «0», устанавливается хорошо отражающий свет объект. После этого программа должна сохранить измеренные значения разности фаз для каждой из частот модуляции. В дальнейшей работе нужно вычитать эти значения из соответствующих значений разностей фаз.
В своем алгоритме определения расстояния я решил использовать три частоты модуляции: 162.5 МГц, 191.5 МГц, 193.5 МГц — по результатам экспериментов, это было наиболее подходящее количество частот.
Мой алгоритм определения расстояния состоит из трех этапов:
- Проверка, не попали ли разности фаз в зону «нулевого» расстояния. В области, близкой к нулю калибровки, из-за ошибок измерения значение разности фаз может «прыгать» — от 0 градусов до 359 градусов, что приводит к большим ошибками при измерении расстояния. Поэтому, при обнаружении, что все три разности фаз одновременно получились близкими к нулю, можно считать, что измеряемое расстояние близко к нулевому значению, и за счет этого отказаться от вычисления величин N.
- Предварительное вычисление расстояния по биениям сигналов с частотами 191.5 МГц и 193.5 МГц. Эти частоты выбраны близкими, за счет чего зона определенности получается достаточно большой:
, но и результат вычислений сильно подвержен влиянию ошибок измерений. При низком уровне принимаемого сигнала ошибка может составлять несколько метров (несколько длин волн).
- Вычисление расстояния методом перебора по разностям фаз сигналов с частотами 162.5 МГц и 191.5 МГц.
Поскольку на предыдущем этапе уже определено приблизительное расстояние, то диапазон перебираемых значений N можно ограничить. За счет этого уменьшается сложность перебора и отбрасываются возможные ошибочные результаты.
В результате у меня получилась вот такая программа для ПК:
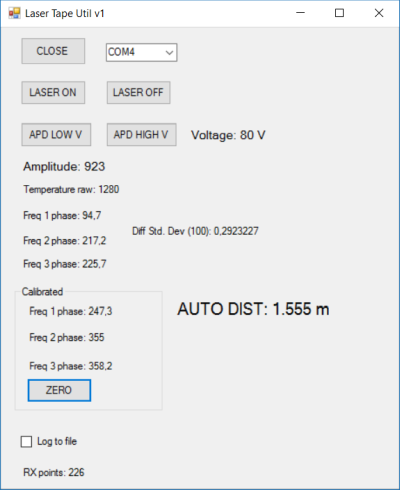
Эта программа позволяет отображать данные, передаваемые рулеткой — амплитуду сигнала, напряжение APD, температуру в единицах АЦП, значения разности фаз сигналов для трех частот и вычисленное по ним расстояние до объекта.
Калибровка нуля производится в самой программе при нажатии кнопки «ZERO».
Для автономно работающего лазерного дальномера важно, чтобы усиление сигнала можно было менять, так как при изменении расстояния и коэффициента отражения уровень сигнала может очень сильно меняться. У себя в программе микроконтроллера я реализовал изменение усиления за счет переключения между двумя напряжениями питания APD — 82 В и 98 В. При переключении напряжения уровень усиления менялся примерно в 10 раз.
Я не стал реализовывать переключение между двумя каналами АЦП — «MCU_signal_high», «MCU_signal_low» — программа микроконтроллера всегда использует сигнал только с канала «MCU_signal_high».
Следующий этап — окончательный, заключается в переносе алгоритма расчета расстояния на микроконтроллер. Благодаря тому, что алгоритм был уже проверен на ПК, это не составило особого труда. Кроме того, в программу микроконтроллера пришлось добавить возможность производить калибровку нуля. Данные этой калибровки микроконтроллер сохраняет во Flash памяти.
Я реализовал два различных варианта прошивки микроконтроллера, отличающихся принципом захвата сигналов. В одной из них, более простой, микроконтроллер во время захвата данных от АЦП ничего не делает. Вторая прошивка — более сложная, в ней данные от АЦП одновременно записываются в один из массивов при помощи DMA, и в то же время при помощи алгоритма Герцеля обрабатываются уже захваченные ранее данные. За счет этого скорость измерений повышается практически в 2 раза по сравнению с простой версией прошивки.
Результат вычислений микроконтроллер отправляет по UART на компьютер.
Для удобства анализа результатов я написал еще одну маленькую программу для ПК:
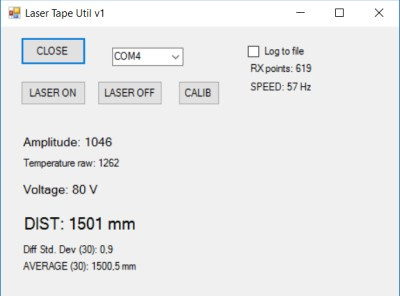
Результаты
В результате мне удалось точно выяснить, как устроена электроника лазерной рулетки, и написать собственную Open source прошивку для нее.
Для меня в процессе написания прошивки наиболее важным было добиться максимальной скорости измерений. К сожалению, повышение скорости измерений заметно сказывается на точности измерений, так что требуется искать компромисс. К примеру, код, приведенный в конце этой статьи, обеспечивает 60 измерений в секунду, и точность при этом составляет около 5-10 мм.
Если уменьшить количество захватываемых значений сигнала, можно повысить скорость измерений. Я получал и 100 измерений в секунду, но при этом влияние шумов значительно увеличивалось.
Конечно же, внешние условия, такие как расстояние до объекта и коэффициент отражения поверхности сильно влияют на отношение сигнал-шум, а следовательно, и на точность измерений. К сожалению, при слишком низком уровне светового сигнал даже увеличение усиления APD не сильно помогает — с ростом усиления растет и уровень шумов.
В ходе экспериментов я заметил, что внешняя засветка лавинного фотодиода тоже значительно увеличивает уровень помех. В модуле, который был у меня, вся электроника открыта, так что для уменьшения помех его приходится накрывать чем-нибудь непрозрачным.
Еще одна замеченная особенность — из-за того, что оптические оси лазера и объектива фотодиода не совпадают, на близких расстояниях (<0.7 м) уровень сигнала значительно падает.
В принципе, уже в таком виде электронику рулетки можно использовать в каком-нибудь проекте, например, в качестве датчика расстояния для робота.
Видео, показывающее работу рулетки:
Напоследок: какие рулетки еще можно встретить?
Здесь я хочу рассказать о конструкциях других лазерных рулеток, о которых можно найти информацию в сети.
- В первую очередь стоит отметить проект реверс-инжиниринга лазерной рулетки BOSCH DLE50.
Особенность этой рулетки — в ней в качестве PLL генератора используется заказная микросхема CF325, на которую в интернете нет никакой документации, что заметно усложняет процесс реверс-инжиниринга. Эта ситуация (заказные микросхемы без документации) очень часто встречается в лазерных рулетках, но, похоже, сейчас ситуация начинает меняться — заказные микросхемы начинают заменятся «универсальными».
Используемый в этой рулетке микроконтроллер — ATmega169P.
Еще одна особенность этой рулетки — использование механического узла, управляемого электромагнитом, который позволяет создавать «оптическое короткое замыкание», то есть перенаправляет свет от лазера к фотодиоду по известному пути. За счет того, что длина пути света и коэффициент отражения при этом известны, микроконтроллер может производить различные калибровки (по амплитуде и фазе). Во время работы этого узла лазерная рулетка достаточно громко щелкает.
Вот здесь можно посмотреть фотографии электроники этой рулетки.
- Достаточно много что известно про лазерную рулетку UT390B.
Некий энтузиаст смог произвести реверс-инжиниринг протокола отладочного UART интерфейса этой рулетки, и научился управлять ее работой. Есть даже библиотека для Arduino.
На русском про устройство этой рулетки можно почитать здесь.
Как видно из фотографий, электроника этой рулетки достаточно проста, и похожа на ту, что описана в этой статье.
Используемый в этой рулетке микроконтроллер — STM32F103C8. Микросхема PLL: CKEL925 (на нее есть документация).
- А вот протокол новой версии рулетки UT390B+ никто пока выяснить не смог. Схемотехника этой рулетки отличается от ее старой версии.
Она еще ближе к схемотехнике моей рулетки — здесь используется микроконтроллер STM32F030CBT6 и PLL Si5351.
Если приглядеться к фотографиям, можно заметить, что в рулетке установлены два лазера.
Судя по всему, два лазера в рулетке сейчас — не редкость. Вот в этом описании устройства еще одной рулетки упоминается, что один из лазеров имеет видимое излучение, и служит только для «целеуказания», а второй лазер — инфракрасный, и используется для измерения расстояния. Интересно, что при этом и лазер, и фотодиод используют одну линзу.
- Еще одна рулетка с неизвестным протоколом — BOSCH PLR 15.
Энтузиасты уже пытались разобраться с ее протоколом, но пока в этом никто не преуспел.
Раньше я тоже пробовал выяснить, как работает эта рулетка, и даже частично восстановил схему этой рулетки.
Используемый в этой рулетке микроконтроллер — STM32F051R6. А вот других микросхем высокой степени интеграции в ней просто нет!
Зато фотоприемник здесь использован очень необычный, я никогда не встречал даже упоминаний таких устройств:

Судя по всему, он представляет собой систему на кристалле, и содержит два фотодиода (измерительный и опорный каналы), усилители фотодиодов, цифровую управляющую электронику и АЦП. Сигнал модуляции лазера идет тоже с него. Сам фотоприемник соединен с микроконтроллером через SPI.
Я пробовал перехватывать данные, которые идут по SPI — там присутствуют команды от контроллера датчику и пакеты информации от датчика контроллеру.
Если обработать эти пакеты в Excel — то явно видны синусоиды (то есть используется фазовый способ измерения расстояния). Это значит, что обработкой сигнала в этой рулетке занимается микроконтроллер.
Однако информации по SPI идет очень много, частоты, на которых идут измерения, установить не удалось, так что даже считать с рулетки расстояние — достаточно проблематичная задача.
Кое-какая информация по аналогичной рулетке Bosch GLM 20 собрана здесь.
- Различные китайские модули.
В последнее время в китайских интернет-магазинах появилось большое количество модулей лазерных дальномеров (из можно найти по запросу «laser ranging module» и аналогичных ему).
Среди них можно найти и модули, которые выглядят абсолютно так же, как и мой, но продаются они в два раза дороже (40$). Похоже, что это все те же внутренности лазерных рулеток, но с модифицированной прошивкой. Интересно, что среди различных конструкций мне несколько раз попадались дальномеры с двумя одинаковыми микросхемами PLL (судя по всему, эти микросхемы — не заказные).
→ Файлы проекта
→ Инструкция по подключению модуля лазерного дальномера к Arduino

