Доброго времени суток, Хабр! Пора вновь вернуться к задачам оптимизации. На этот раз мы займемся линейной регрессией и разберемся, кто же такие коты — только пушистые домашние мерзавцы животные или еще и неплохой инструмент для решения прикладных задач.

За прошедшее время (а его прошло немало) я немного «причесал» репозиторий, написал более-менее несущие смысл ReadMe, а также провел реструктуризацию проектов. Что изменилось с момента прошлой статьи, и каково состояние проекта на данный момент?
Как я и обещал в первой работе, в начале статьи я буду обозначать круг задач, которые будут решаться, и затем останавливаться на каждой более подробно. Ссылки на репозиторий будут приведены в конце.
Итак, в этой работе мы поговорим:
Начнем с формулирования задачи регрессии.
Пусть имеется набор измерений, который удобно представить в виде матрицы: представляется вектором из
представляется вектором из  . Также имеется набор значений зависимой переменной
. Также имеется набор значений зависимой переменной  — вектор параметров модели, т.ч.
— вектор параметров модели, т.ч.  . Очевидно, что задача аппроксимации и регрессии тесно связаны.
. Очевидно, что задача аппроксимации и регрессии тесно связаны.
Таким образом, если вы экспертно зафиксировали форму желаемой модели, то вся задача сводится к определению значений вектора параметров . Следует отметить, что для машинного обучения действует следующий принцип: чем больше у модели степеней свободы (читай параметров), тем более вероятно, что используемая модель переобучится. В случае же если степеней свободы немного, то есть все шансы, что модель не будет достаточно точной.
. Следует отметить, что для машинного обучения действует следующий принцип: чем больше у модели степеней свободы (читай параметров), тем более вероятно, что используемая модель переобучится. В случае же если степеней свободы немного, то есть все шансы, что модель не будет достаточно точной.
В этом плане линейные модели являются, наверное, некоторым переходным звеном. Несмотря на кажущуюся простоту, для многих ситуаций они с достаточно высокой точностью решают задачу регрессии. Тем не менее, при сильной зашумленности данных линейные модели порой нуждаются в искусственном ограничении (регуляризации).
Как это принято, начнем с наиболее простой модели и будем ее по-тихоньку усложнять. Итак, в общем случае линейная регрессия задается следующей формулой: равна размерности вектора измерений плюс один. Нулевая компонента называется смещением (bias term или intercept term). По аналогии с простой функцией
равна размерности вектора измерений плюс один. Нулевая компонента называется смещением (bias term или intercept term). По аналогии с простой функцией  , где константа
, где константа  отвечает за смещение графика относительно оси абсцисс.
отвечает за смещение графика относительно оси абсцисс.
Таким образом, линейную модель можно выразить через скалярное произведение
Удобно поставить задачу поиска оптимального значения вектора параметров с помощью остаточной суммы квадратов (RSS, residual sum of squares)
с помощью остаточной суммы квадратов (RSS, residual sum of squares)  получается из матрицы
получается из матрицы  путем добавления слева столбца, состоящего из единиц.
путем добавления слева столбца, состоящего из единиц.
Как видно из приведенного выше описания, задача оптимизации уже поставлена. Так что в дальнейшем останется лишь применить к ней выбранный алгоритм оптимизации.
В случае если необходимо по тем или иным причинам уменьшить степень вариативности модели без ее структурного изменения, можно использовать регуляризацию, которая накладывает ограничения на параметры модели.
Ridge regression (гребневая регрессия) использует L2 регуляризацию параметров модели: — L2 норма. Параметр
— L2 норма. Параметр  отвечает за сжатие коэффициентов: с увеличением
отвечает за сжатие коэффициентов: с увеличением  параметры модели стремятся к нулю. Наглядно это очень хорошо продемонстрировано на официальном сайте пакета scikit:
параметры модели стремятся к нулю. Наглядно это очень хорошо продемонстрировано на официальном сайте пакета scikit:
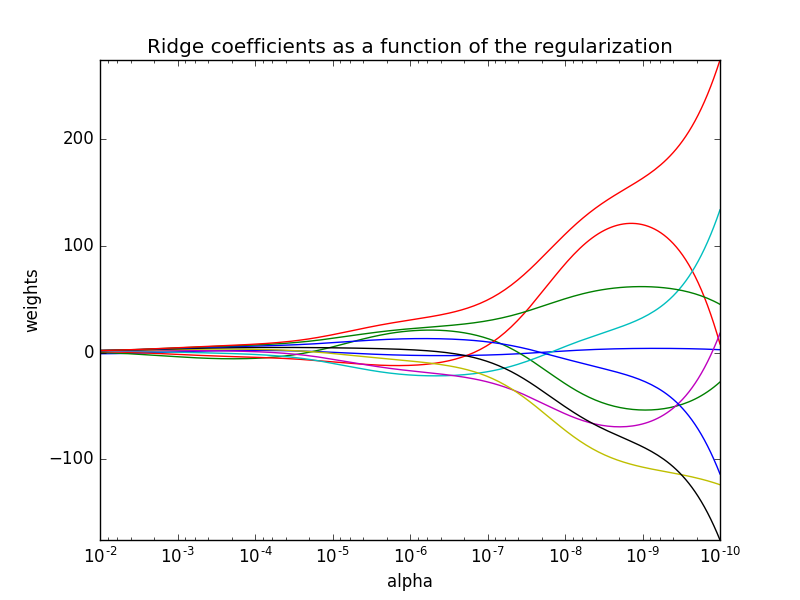
Как и в случае с простой линейной регрессией для гребневой регрессии имеется возможность аналитически выразить решение: — единичная матрица порядка
— единичная матрица порядка  , в левом верхнем углу которой находится ноль.
, в левом верхнем углу которой находится ноль.
Для Lasso Regression постановка задачи похожая, разница заключается в том, что теперь используется L1 регуляризация параметров модели: — L1 норма
— L1 норма
Таким образом, с точки зрения оптимизации, Ridge regression и Lasso Regression отличаются лишь способом постановки задачи минимизации.
Как уже стало ясно из названия, алгоритм имитирует поведение животных семейства кошачьих (в том числе и домашних кошек). Что Вы можете сказать о своем домашнем любимце? Он может отыгрывать роль милого лежебоки (хотя мы на самом деле знаем, какие коварные мысли роятся в его голове), может вообразить себя великим (но осторожным) исследователем, а может просто носиться по квартире за несуществующим (а точнее невидимым вам) соперником. Лежащих и недвижимых словно Великая Китайская стена котов мы оставим в покое, пусть себе отдыхают, а вот на последних двух действиях остановимся подробнее. Для любого алгоритма оптимизации хорошо иметь несколько стадий поиска: глобального, в ходе которого мы должны попасть в область притяжения локального экстремума (а в идеале — глобального), и уточняющего, в ходе которого мы должны придвинуться из окрестности экстремума ближе к его истинному расположению. Ничего не напоминает? В самом деле, коты, гоняющиеся за незримым врагом, — явные кандидаты на реализацию процедуры глобального поиска, а вот аккуратные исследователи помогут вам найти оптимальное место для отдыха. Эти две эвристики лежат в основе алгоритма Cat Swarm Optimization. Для полной картины остается представить, что у вас не один кот, а целая стая. Но так ведь даже лучше, верно?
Псевдокод алгоритма представлен ниже:
Если же постараться формализовать все идеи, то в математическом выражении мы имеем следующие тезисы:
Итак, что же представляют из себя режимы, в которых могут находиться коты? Тут все просто.
Во время режима поиска из текущего положения генерируются новые возможные положения
генерируются новые возможные положения  . Новое положение выбирается выбирается по методу рулетки, где вероятность выборка
. Новое положение выбирается выбирается по методу рулетки, где вероятность выборка  -го положения определяется по формуле
-го положения определяется по формуле
Теперь немного о том, как реализуется погоня. Чтобы не пугать хозяина, все-таки следует гоняться не за вымышленным врагом, а за вполне реальным — котом, который на данный момент нашел себе лучшее место (его позиция будет обозначаться ). Скорость кота меняется по следующему правилу:
). Скорость кота меняется по следующему правилу:  — равномерно распределенная случайная величина, а
— равномерно распределенная случайная величина, а  — константа скорости (та самая, которая отвечает за поворотливость). Новое положение кота рассчитывается следующим образом:
— константа скорости (та самая, которая отвечает за поворотливость). Новое положение кота рассчитывается следующим образом:  .
.
Теперь, когда все основные моменты алгоритма перечислены, пора уже разобраться, смогут ли коты построить регрессию?
Сгенерируем несколько тестовых наборов данных (в тетрадке также есть расчет с моделей регрессий с помощью scikit):
 — равномерно распределенная случайная величина.
— равномерно распределенная случайная величина.
Видно, что найденные значения достаточно близки к результатам, полученными с помощью scikit.
Таким образом, приведенная постановка задачи, несмотря на свою модельность и простоту, позволила познакомиться с метаэвристическим алгоритмом Cat Swarm Optimization. При разработке оптимизационных процедур зачастую полезно позаниматься наблюдением за окружающим миром, ведь, как известно, «природа знает лучше».
Ссылки и литература

За прошедшее время (а его прошло немало) я немного «причесал» репозиторий, написал более-менее несущие смысл ReadMe, а также провел реструктуризацию проектов. Что изменилось с момента прошлой статьи, и каково состояние проекта на данный момент?
- в проекте Algebras находятся реализация trait'а алгебры, в котором перечислены все основные операции, которые должны быть реализованы для объекта, наследующего его; кроме того, в данном проекте на текущий момент реализованы вещественная и интервальная алгебры,
- в проекте Transformations находятся основные типы преобразований с соответствующими связями; в данном проекте было сделано дополнение свойств преобразований (например, численная дифференциуремость), что пригодится в дальнейшем при реализации алгоритмов оптимизации, использующих градиент,
- в проекте Algorithms находятся основные классы алгоритмов; данный проект будет наполняться по мере выделения общих типов алгоритмов (пока здесь есть лишь алгоритм оптимизации вещественнозначных функций),
- в проектах Metaheuristic Optimization и Machine Learning хранятся реализации алгоритмов оптимизации и машинного обучения соответственно,
- в проекте Tools собраны различные процедуры, необходимые для функционирования работы алгоритмов (например, генераторы случайных чисел в соответствии с распределениями).
Как я и обещал в первой работе, в начале статьи я буду обозначать круг задач, которые будут решаться, и затем останавливаться на каждой более подробно. Ссылки на репозиторий будут приведены в конце.
Итак, в этой работе мы поговорим:
- о линейных моделях регрессии,
- о способах сведения задачи поиска линейной регрессии к задаче оптимизации,
- о метаэвристическом алгоритме глобальной условной оптимизации, моделирующем поведение котов.
Линейные модели регрессии и как их свести к задаче оптимизации
Начнем с формулирования задачи регрессии.
Пусть имеется набор измерений, который удобно представить в виде матрицы:
Таким образом, если вы экспертно зафиксировали форму желаемой модели, то вся задача сводится к определению значений вектора параметров
В этом плане линейные модели являются, наверное, некоторым переходным звеном. Несмотря на кажущуюся простоту, для многих ситуаций они с достаточно высокой точностью решают задачу регрессии. Тем не менее, при сильной зашумленности данных линейные модели порой нуждаются в искусственном ограничении (регуляризации).
Код общей модели линейной регрессии
В одноименном объекте имеются
trait GeneralizedLinearModel {
def getWeights(): Vector[Real]
def apply(v: Vector[Real]): Real = getWeights().dot(v + bias)
def apply(vectors: Seq[Vector[Real]]): Seq[Real] = vectors.map(this.apply(_))
def convertToTransformation(): InhomogeneousTransformation[Vector[Real], Real] =
new InhomogeneousTransformation[Vector[Real], Real](v => this.apply(v))
}
object GeneralizedLinearModel {
val bias = Vector("bias" -> Real(1.0))
object Metrics {
def RSS(generalizedLinearModel: GeneralizedLinearModel, input: Seq[Vector[Real]], output: Seq[Real]): Real = {
val predictions = generalizedLinearModel(input)
predictions.zip(output)
.map { case (pred, real) => (pred - real) ^ 2.0 }
.reduce(_ + _) / input.length
}
}
}
- метод, возвращающий веса модели регрессии,
- apply — метод, рассчитывающий значение зависимой переменной на основе полученного входа,
- конвертация к неоднородному преобразованию.
В одноименном объекте имеются
- константа, отвечающая за сдвиг,
- метрика RSS.
Ordinary Least Squares
Как это принято, начнем с наиболее простой модели и будем ее по-тихоньку усложнять. Итак, в общем случае линейная регрессия задается следующей формулой:
Таким образом, линейную модель можно выразить через скалярное произведение
Удобно поставить задачу поиска оптимального значения вектора параметров
Как видно из приведенного выше описания, задача оптимизации уже поставлена. Так что в дальнейшем останется лишь применить к ней выбранный алгоритм оптимизации.
Ordinary Least Squares
case class OrdinaryLeastSquaresRegression(w: Vector[Real]) extends GeneralizedLinearModel {
override def getWeights(): Vector[Real] = w
}
object OrdinaryLeastSquaresRegression {
class Task(input: Seq[Vector[Real]], output: Seq[Real]) extends General.Task {
def toOptimizationTask(searchArea: Map[String, (Double, Double)]): (Optimization.Real.Task, InhomogeneousTransformation[Vector[Real], OrdinaryLeastSquaresRegression]) = {
val vectorToRegressor =
new InhomogeneousTransformation[Vector[Real], OrdinaryLeastSquaresRegression]((w: Vector[Real]) => OrdinaryLeastSquaresRegression(w))
val task = new Optimization.Real.Task(
new Function[Real]((w: Vector[Real]) =>
GeneralizedLinearModel.Metrics.RSS(vectorToRegressor(w), input, output)), searchArea)
(task, vectorToRegressor)
}
}
}Ridge & Lasso Regression
В случае если необходимо по тем или иным причинам уменьшить степень вариативности модели без ее структурного изменения, можно использовать регуляризацию, которая накладывает ограничения на параметры модели.
Ridge regression (гребневая регрессия) использует L2 регуляризацию параметров модели:

Как и в случае с простой линейной регрессией для гребневой регрессии имеется возможность аналитически выразить решение:
Ridge Regression
class RidgeRegression(w: Vector[Real], alpha: Double) extends OrdinaryLeastSquaresRegression(w) { }
object RidgeRegression {
class Task(input: Seq[Vector[Real]], output: Seq[Real]) extends General.Task {
def toOptimizationTask(searchArea: Map[String, (Double, Double)], alpha: Double): (Optimization.Real.Task, InhomogeneousTransformation[Vector[Real], RidgeRegression]) = {
val vectorToRegressor =
new InhomogeneousTransformation[Vector[Real], RidgeRegression]((w: Vector[Real]) => new RidgeRegression(w, alpha))
val task = new Optimization.Real.Task(
new Function[Real]((w: Vector[Real]) =>
GeneralizedLinearModel.Metrics.RSS(vectorToRegressor(w), input, output) +
alpha * w.components.filterKeys(_ != "bias").values.map(_ ^ 2.0).reduce(_ + _)), searchArea)
(task, vectorToRegressor)
}
}
}Для Lasso Regression постановка задачи похожая, разница заключается в том, что теперь используется L1 регуляризация параметров модели:
Lasso Regression
class LassoRegression(w: Vector[Real], alpha: Double) extends OrdinaryLeastSquaresRegression(w) { }
object LassoRegression {
class Task(input: Seq[Vector[Real]], output: Seq[Real]) extends General.Task {
def toOptimizationTask(searchArea: Map[String, (Double, Double)], alpha: Double): (Optimization.Real.Task, InhomogeneousTransformation[Vector[Real], LassoRegression]) = {
val vectorToRegressor =
new InhomogeneousTransformation[Vector[Real], LassoRegression]((w: Vector[Real]) => new LassoRegression(w, alpha))
val task = new Optimization.Real.Task(
new Function[Real]((w: Vector[Real]) =>
GeneralizedLinearModel.Metrics.RSS(vectorToRegressor(w), input, output) / (2.0 * input.length) +
alpha * w.components.filterKeys(_ != "bias").values.map(Algebra.abs(_)).reduce(_ + _)), searchArea)
(task, vectorToRegressor)
}
}
}Таким образом, с точки зрения оптимизации, Ridge regression и Lasso Regression отличаются лишь способом постановки задачи минимизации.
Cat Swarm Optimization
Как уже стало ясно из названия, алгоритм имитирует поведение животных семейства кошачьих (в том числе и домашних кошек). Что Вы можете сказать о своем домашнем любимце? Он может отыгрывать роль милого лежебоки (хотя мы на самом деле знаем, какие коварные мысли роятся в его голове), может вообразить себя великим (но осторожным) исследователем, а может просто носиться по квартире за несуществующим (а точнее невидимым вам) соперником. Лежащих и недвижимых словно Великая Китайская стена котов мы оставим в покое, пусть себе отдыхают, а вот на последних двух действиях остановимся подробнее. Для любого алгоритма оптимизации хорошо иметь несколько стадий поиска: глобального, в ходе которого мы должны попасть в область притяжения локального экстремума (а в идеале — глобального), и уточняющего, в ходе которого мы должны придвинуться из окрестности экстремума ближе к его истинному расположению. Ничего не напоминает? В самом деле, коты, гоняющиеся за незримым врагом, — явные кандидаты на реализацию процедуры глобального поиска, а вот аккуратные исследователи помогут вам найти оптимальное место для отдыха. Эти две эвристики лежат в основе алгоритма Cat Swarm Optimization. Для полной картины остается представить, что у вас не один кот, а целая стая. Но так ведь даже лучше, верно?
Псевдокод алгоритма представлен ниже:
Шаг 1. Инициализировать популяцию из N котов.
Шаг 2. Определить приспособленность каждого кота на основе его позиции в исследуемом пространстве. Запомнить "лучшего" кота (в терминологии задачи минимизации, ему будет соответствовать наименьшее значение функции).
Шаг 3. Переместить котов в соответствии с их процедурой смещения (поиск или погоня).
Шаг 4. Заново присвоить котам режимы перемещения в соответствии с параметром MR.
Шаг 5. Проверить условие окончания работы. В случае его невыполнения перейти к шагу 2.
Если же постараться формализовать все идеи, то в математическом выражении мы имеем следующие тезисы:
- каждый кот ассоциирован с некоторой точкой в исследуемом пространстве,
- приспособленность кота — значение оптимизируемой функции в точке, соответствующей его текущему положению,
- каждый кот может находиться в одном из двух режимов: поиск или погоня.
- итерация алгоритма подразумевает реализацию процесса перемещения в соответствии с тем режимом, в котором находится кот.
Параметры, влияющие на работу алгоритма
class CatSwarmOptimization(numberOfCats: Int, MR: Double,
SMP: Int, SRD: Double, CDC: Int, SPC: Boolean,
velocityConstant: Double, velocityRatio: Double,
generator: DiscreteUniform with ContinuousUniform = Kaimere.Tools.Random.GoRN) extends Algorithm
- количество котов (numberOfCats) — чем больше котов, тем дольше время работы алгоритма (если его ограничивать количеством итераций), но и потенциально большая точность найденного ответа,
- пропорция котов в режиме поиска и погони (MR) — данный параметр позволяет направлять поиск по той стратегии, которую пользователь считает предпочтительной; например, если вы заведомо знаете окрестность, в которой лежит глобальный оптимум, то логично инициализировать популяцию в этой окрестности и поддерживать большее число котов-исследователей в популяции для уточнения первоначального решения,
- количество попыток для режима поиска (SMP) — сколько разных смещений будет производить кот-исследователь; большие значения данного параметра увеличивают время одной итерации, но позволяют увеличить точность определения положения экстремума,
- доля смещения для режима поиска (SRD) — доля, на которую кот-исследователь смещается относительно своего текущего положения, большие значений смещают уточняющий поиск в сторону глобального,
- количество направлений, по которым ведется поиск (CDC) — данный параметр регулирует количество измерений, которые будут изменять у текущего положения кота, находящегося в режиме поиска; меньшие значения делают поиск покоординатным,
- желание остаться на старом месте (SPC) — булева переменная, которая позволяет выбирать, может ли кот-исследователь остаться не текущем месте,
- константа скорости (velocityConstant) — определяет степень поворотливости кота во время погони; большие значения быстрее меняют текущий вектор скорости кота,
- максимальная скорость (velocityRatio) — все-таки вы в доме хозяин, поэтому в случае если кто-то из котов слишком уж разогнался, то вы вполне можете на него прикрикнуть,
чтобы он притормозил, т.о. данный параметр ограничивает максимальную скорость движения котов.
Итак, что же представляют из себя режимы, в которых могут находиться коты? Тут все просто.
Во время режима поиска из текущего положения
Теперь немного о том, как реализуется погоня. Чтобы не пугать хозяина, все-таки следует гоняться не за вымышленным врагом, а за вполне реальным — котом, который на данный момент нашел себе лучшее место (его позиция будет обозначаться
Реализация кота
case class Cat(location: Vector[Real], velocity: Vector[Real])(implicit generator: DiscreteUniform with ContinuousUniform) {
def getFromSeries[T](data: Seq[T], n: Int, withReturn: Boolean): Seq[T] =
withReturn match {
case true => Seq.fill(n)(generator.getUniform(0, data.size - 1)).map(x => data(x))
case false => data.sortBy(_ => generator.getUniform(0.0, 1.0)).take(n)
}
def seek(task: Task, SPC: Boolean, SMP: Int, CDC: Int, SRD: Double): Cat = {
val newLocations = (if (SPC) Seq(location) else Seq()) ++
Seq.fill(SMP - (if (SPC) 1 else 0))(location)
.map { loc =>
val ratio =
getFromSeries(task.searchArea.keys.toSeq, CDC, false)
.map { key => (key, generator.getUniform(1.0 - SRD, 1.0 + SRD)) }.toMap
(loc * ratio).constrain(task.searchArea)
}
val fitnessValues = newLocations.map(task(_)).map(_.value)
val newLocation =
if (fitnessValues.tail.forall(_ == fitnessValues.head)) newLocations(generator.getUniform(0, SMP - 1))
else {
val maxFitness = fitnessValues.max
val minFitness = fitnessValues.min
val probabilities = fitnessValues.map(v => (maxFitness - v) / (maxFitness - minFitness))
val roulette =
0.0 +: probabilities.tail
.foldLeft(Seq(probabilities.head)) { case (prob, curr) => (curr + prob.head) +: prob }
.reverse
val chosen = generator.getUniform(0.0, roulette.last)
val idChosen = roulette.sliding(2).indexWhere{ case Seq(a, b) => a <= chosen && chosen <= b}
newLocations(idChosen)
}
new Cat(newLocation, newLocation - this.location)
}
def updateVelocity(bestCat: Cat, velocityConstant: Double, maxVelocity: Map[String, Double]): Vector[Real] = {
val newVelocity = this.velocity + (bestCat.location - this.location) * velocityConstant * generator.getUniform(0.0, 1.0)
Vector(newVelocity.components
.map { case (key, value) =>
if (value.value > maxVelocity(key)) (value, Real(maxVelocity(key)))
if (value.value < -maxVelocity(key)) (value, Real(-maxVelocity(key)))
(key, value)
})
}
def trace(task: Task, bestCat: Cat, velocityConstant: Double, maxVelocity: Map[String, Double]): Cat = {
val newVelocity = this.updateVelocity(bestCat, velocityConstant, maxVelocity)
val newLocation = (location + newVelocity).constrain(task.searchArea)
new Cat(newLocation, newVelocity)
}
def move(mode: Int, task: Task, bestCat: Cat, SPC: Boolean, SMP: Int, CDC: Int, SRD: Double, velocityConstant: Double, maxVelocity: Map[String, Double]): Cat = mode match {
case 0 => seek(task, SPC, SMP, CDC, SRD)
case 1 => trace(task, bestCat, velocityConstant, maxVelocity)
}
}Теперь, когда все основные моменты алгоритма перечислены, пора уже разобраться, смогут ли коты построить регрессию?
Так умеют ли коты строить регрессию или нет?
Сгенерируем несколько тестовых наборов данных (в тетрадке также есть расчет с моделей регрессий с помощью scikit):
- одномерная линейная зависимость без шума:
,
- параметры модели Ordinary Least Squares:
,
- параметры модели Ridge Regression (
):
,
- параметры модели Lasso Regression (
):
,
- параметры модели Ordinary Least Squares:
- многомерная линейная зависимость без шума:
,
- параметры модели Ordinary Least Squares:
,
- параметры модели Ridge Regression (
):
,
- параметры модели Lasso Regression (
):
,
- параметры модели Ordinary Least Squares:
- одномерная линейная зависимость с шумом:
,
- параметры модели Ordinary Least Squares:
,
- параметры модели Ridge Regression (
):
,
- параметры модели Lasso Regression (
):
,
- параметры модели Ordinary Least Squares:
- многомерная линейная зависимость с шумом:
,
- параметры модели Ordinary Least Squares:
,
- параметры модели Ridge Regression (
):
,
- параметры модели Lasso Regression (
):
,
- параметры модели Ordinary Least Squares:
Результаты, полученные с помощью пакета scikit для данных с шумом
Для одномерной линейной зависимости с шумом:
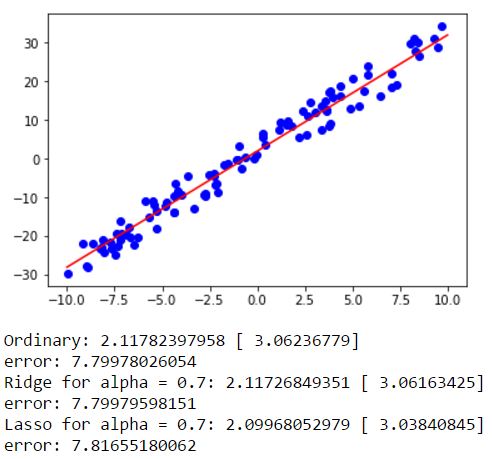
Для многомерной линейной зависимости с шумом:


Для многомерной линейной зависимости с шумом:

Видно, что найденные значения достаточно близки к результатам, полученными с помощью scikit.
Заключение
Таким образом, приведенная постановка задачи, несмотря на свою модельность и простоту, позволила познакомиться с метаэвристическим алгоритмом Cat Swarm Optimization. При разработке оптимизационных процедур зачастую полезно позаниматься наблюдением за окружающим миром, ведь, как известно, «природа знает лучше».
Ссылки и литература
- Код проекта
- Описание линейных моделей регрессии: [1], [2]
- Книжка по машинному обучению
- Статья по Cat Swarm Optimization