Содержание
- Часть 1: Введение
- Часть 2: Manifold learning и скрытые (latent) переменные
- Часть 3: Вариационные автоэнкодеры (VAE)
- Часть 4: Conditional VAE
- Часть 5: GAN (Generative Adversarial Networks) и tensorflow
- Часть 6: VAE + GAN
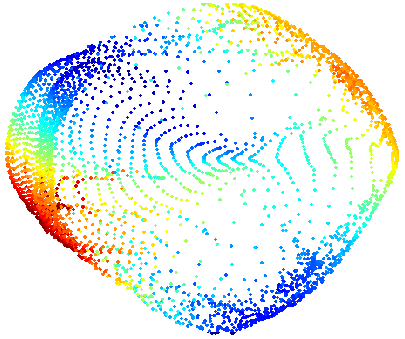
Для того, чтобы лучше понимать, как работают автоэнкодеры, а также чтобы в последствии генерировать из кодов что-то новое, стоит разобраться в том, что такое коды и как их можно интерпретировать.
Manifold learning
Изображения цифр mnist (на которых примеры в прошлой части) — это элементы
Однако среди всех изображений, изображения цифр занимают лишь ничтожную часть, абсолютное же большинство изображений — это просто шум.
С другой стороны, если взять произвольное изображение цифры, то и все изображения из некоторой окрестности также можно считать цифрой.
А если взять два произвольных изображения цифры, то в изначальном 784-мерном пространстве скорее всего, можно найти непрерывную кривую, все точки вдоль которой можно также считать цифрами (хотя бы для изображений цифр одного лейбла), а вкупе с предыдущим замечанием, то и все точки некоторой области вдоль этой кривой.
Таким образом, в пространстве всех изображений есть некоторое подпространство меньшей размерности в области вокруг которого сосредоточились изображения цифр. То есть, если наша генеральная совокупность — это все изображения цифр, которые могут быть нарисованы в принципе, то плотность вероятности встретить такую цифру в пределах области сильно выше, чем вне.
Автоэнкодеры с размерностью кода k ищут k-мерное многообразие в пространстве объектов, которое наиболее полно передает все вариации в выборке. А сам код задает параметризацию этого многообразия. При этом энкодер сопоставляет объекту его параметр на многообразии, а декодер параметру сопоставляет точку в пространстве объектов.
Чем больше размерность кодов, тем больше вариаций в данных автоэнкодер сможет передать. Если размерность кодов слишком мала, автоэнкодер запомнит нечто среднее по недостающим вариациям в заданной метрике (это одна из причин, почему mnist цифры все более размытые при снижении размерности кода в автоэнкодерах).
Для того, чтобы лучше понять, что такое manifold learning, создадим простой двумерный датасет в виде кривой плюс шум и будем обучать на нем автоэнкодер.
Код и визуализация
# Импорт необходимых библиотек
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# Создание датасета
x1 = np.linspace(-2.2, 2.2, 1000)
fx = np.sin(x1)
dots = np.vstack([x1, fx]).T
noise = 0.06 * np.random.randn(*dots.shape)
dots += noise
# Цветные точки для отдельной визуализации позже
from itertools import cycle
size = 25
colors = ["r", "g", "c", "y", "m"]
idxs = range(0, x1.shape[0], x1.shape[0]//size)
vx1 = x1[idxs]
vdots = dots[idxs]
# Визуализация
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1])
plt.plot(x1, fx, color="red", linewidth=4)
plt.grid(False)

На картинке выше: синие точки — данные, а красная кривая – многообразие, определяющее наши данные.
Линейный сжимающий автоэнкодер
Самый простой автоэнкодер — это двухслойный сжимающий автоэнкодер с линейными функциями активации (больше слоев не имеет смысла при линейной активации).
Такой автоэнкодер ищет аффинное (линейное со сдвигом) подпространство в пространстве объектов, которое описывает наибольшую вариацию в объектах, тоже самое делает и PCA (метод главных компонент) и оба они находят одно и тоже подпространство
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
def linear_ae():
input_dots = Input((2,))
code = Dense(1, activation='linear')(input_dots)
out = Dense(2, activation='linear')(code)
ae = Model(input_dots, out)
return ae
ae = linear_ae()
ae.compile(Adam(0.01), 'mse')
ae.fit(dots, dots, epochs=15, batch_size=30, verbose=0)
# Применение линейного автоэнкодера
pdots = ae.predict(dots, batch_size=30)
vpdots = pdots[idxs]
# Применение PCA
from sklearn.decomposition import PCA
pca = PCA(1)
pdots_pca = pca.inverse_transform(pca.fit_transform(dots))
Визуализация
# Визуализация
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(x1, fx, color="red", linewidth=4, zorder=10)
plt.plot(pdots[:,0], pdots[:,1], color='white', linewidth=12, zorder=3)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)
plt.scatter(vpdots[:,0], vpdots[:,1], color=colors*5, marker='*', s=150, zorder=5)
plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6)
plt.grid(False)
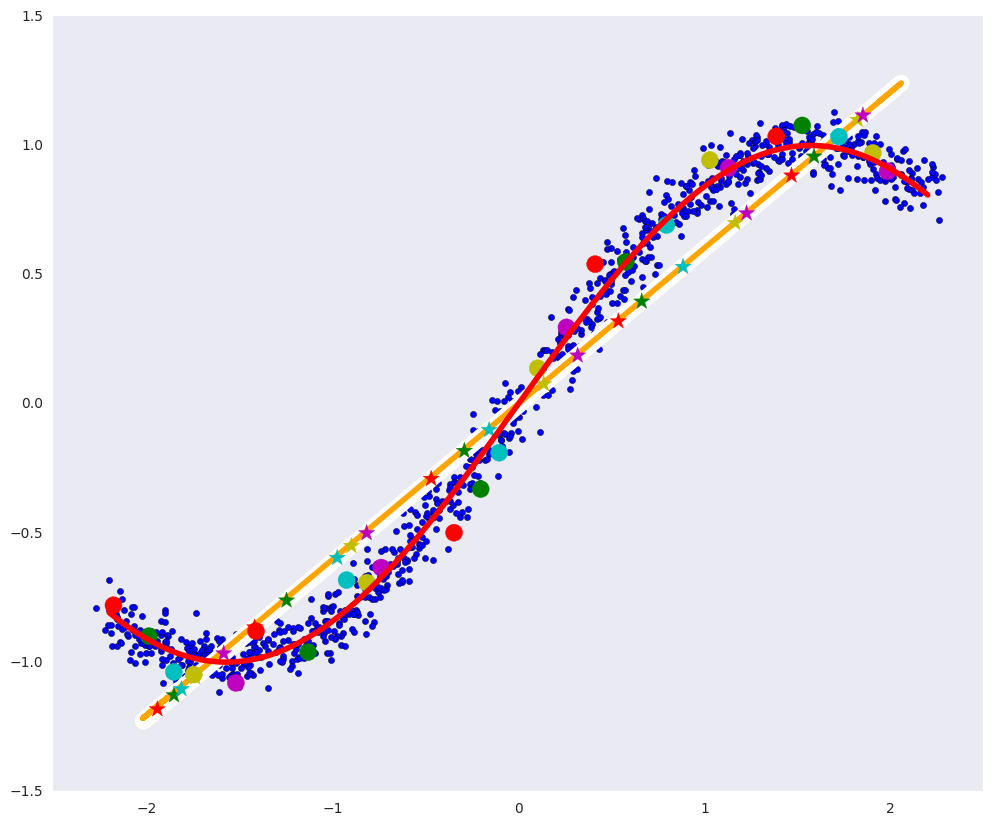
На картинке выше:
- белая линия – многообразие, в которое переходят синие точки данных после автоэнкодера, то есть попытка автоэнкодера построить многообразие, определяющее больше всего вариаций в данных,
- оранжевая линия – многообразие, в которое переходят синие точки данных после PCA,
- разноцветные кружки — точки, которые переходят в звездочки соответствующего цвета после автоэнкодера,
- разноцветные звездочки – соответственно, образы кружков после автоэнкодера.
Автоэнкодер, ищущий линейные зависимости, может быть не так полезен, как автоэнкодер, который может находить произвольные зависимости в данных. Полезно было бы, если бы и энкодер, и декодер могли аппроксимизировать произвольные функции. Если добавить и в энкодер, и в декодер еще хотя бы по одному слою достаточного размера и нелинейную функцию активации между ними, то они смогут находить произвольные зависимости.
Глубокий автоэнкодер
У глубокого автоэнкодера больше число слоев и самое главное — нелинейная функция активации между ними (в нашем случае ELU — Exponential Linear Unit).
def deep_ae():
input_dots = Input((2,))
x = Dense(64, activation='elu')(input_dots)
x = Dense(64, activation='elu')(x)
code = Dense(1, activation='linear')(x)
x = Dense(64, activation='elu')(code)
x = Dense(64, activation='elu')(x)
out = Dense(2, activation='linear')(x)
ae = Model(input_dots, out)
return ae
dae = deep_ae()
dae.compile(Adam(0.003), 'mse')
dae.fit(dots, dots, epochs=200, batch_size=30, verbose=0)
pdots_d = dae.predict(dots, batch_size=30)
vpdots_d = pdots_d[idxs]
Визуализация
# Визуализация
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(x1, fx, color="red", linewidth=4, zorder=10)
plt.plot(pdots_d[:,0], pdots_d[:,1], color='white', linewidth=12, zorder=3)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)
plt.scatter(vpdots_d[:,0], vpdots_d[:,1], color=colors*5, marker='*', s=150, zorder=5)
plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6)
plt.grid(False)
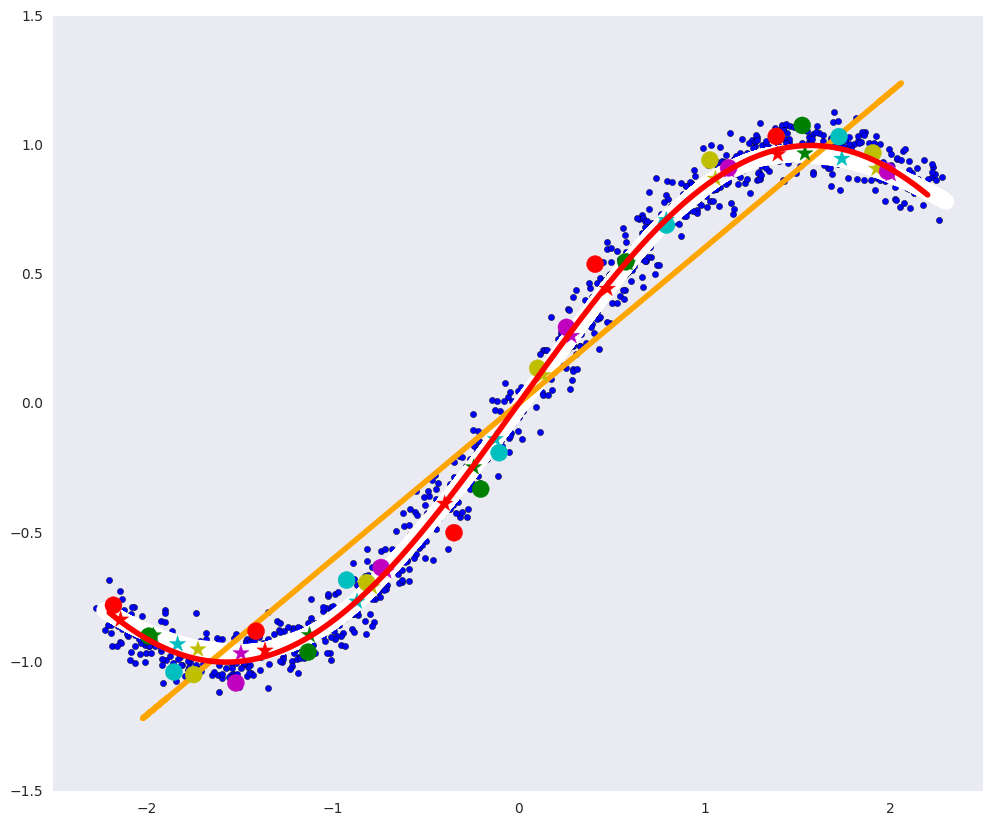
У такого автоэнкодера практически идеально получилось построить определяющее многообразие: белая кривая почти совпадает с красной.
Глубокий автоэнкодер теоретически сможет найти многообразие произвольной сложности, например, такое, около которого лежат цифры в 784-мерном пространстве.
Если взять два объекта и посмотреть на объекты, лежащие на произвольной кривой между ними, то скорее всего промежуточные объекты не будут принадлежать генеральной совокупности, т. к. многообразие на котором лежит генеральная совокупность может быть сильно искривленным и малоразмерным.
Вернемся к датасету рукописных цифр из предыдущей части.
Сначала двигаемся по прямой в пространстве цифр от одной 8-ки к другой:
Код
from keras.layers import Conv2D, MaxPooling2D, UpSampling2D
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
# Сверточный автоэнкодер
def create_deep_conv_ae():
input_img = Input(shape=(28, 28, 1))
x = Conv2D(128, (7, 7), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(32, (2, 2), activation='relu', padding='same')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
encoded = Conv2D(1, (7, 7), activation='relu', padding='same')(x)
# На этом моменте представление (7, 7, 1) т.е. 49-размерное
input_encoded = Input(shape=(7, 7, 1))
x = Conv2D(32, (7, 7), activation='relu', padding='same')(input_encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(128, (2, 2), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (7, 7), activation='sigmoid', padding='same')(x)
# Модели
encoder = Model(input_img, encoded, name="encoder")
decoder = Model(input_encoded, decoded, name="decoder")
autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
return encoder, decoder, autoencoder
c_encoder, c_decoder, c_autoencoder = create_deep_conv_ae()
c_autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
c_autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
def plot_digits(*args):
args = [x.squeeze() for x in args]
n = min([x.shape[0] for x in args])
plt.figure(figsize=(2*n, 2*len(args)))
for j in range(n):
for i in range(len(args)):
ax = plt.subplot(len(args), n, i*n + j + 1)
plt.imshow(args[i][j])
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
# Гомотопия по прямой между объектами или между кодами
def plot_homotopy(frm, to, n=10, decoder=None):
z = np.zeros(([n] + list(frm.shape)))
for i, t in enumerate(np.linspace(0., 1., n)):
z[i] = frm * (1-t) + to * t
if decoder:
plot_digits(decoder.predict(z, batch_size=n))
else:
plot_digits(z)
# Гомотопия между первыми двумя восьмерками
frm, to = x_test[y_test == 8][1:3]
plot_homotopy(frm, to)

Если же двигаться по кривой между кодами (и если многообразие кодов хорошо параметризовано), то декодер переведет эту кривую из пространства кодов, в кривую, не покидающую определяющее многообразие в пространстве объектов. То есть промежуточные объекты на кривой будут принадлежать генеральной совокупности.
codes = c_encoder.predict(x_test[y_test == 8][1:3])
plot_homotopy(codes[0], codes[1], n=10, decoder=c_decoder)

Промежуточные цифры — вполне себе хорошие восьмерки.
Таким образом, можно сказать, что автоэнкодер, по крайней мере локально, выучил форму определяющего многообразия.
Переобучение автоэнкодера
Для того чтобы автоэнкодер мог научиться вычленять какие-то сложные закономерности, обобщающие способности энкодера и декодера должны быть ограничены, иначе даже автоэнкодер с одномерным кодом сможет просто провести одномерную кривую через каждую точку в обучающей выборке, т.е. просто запомнить каждый объект. Но это сложное многообразие, которое построит автоэнкодер, не будет иметь много общего с определяющим генеральную совокупность многообразием.
Возьмем ту же задачу с искусственными данными, обучим тот же глубокий автоэнкодер на очень маленьком подмножестве точек и посмотрим на получившееся многообразие:
Код
dae = deep_ae()
dae.compile(Adam(0.0003), 'mse')
x_train_oft = np.vstack([dots[idxs]]*4000)
dae.fit(x_train_oft, x_train_oft, epochs=200, batch_size=15, verbose=1)
pdots_d = dae.predict(dots, batch_size=30)
vpdots_d = pdots_d[idxs]
plt.figure(figsize=(12, 10))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(x1, fx, color="red", linewidth=4, zorder=10)
plt.plot(pdots_d[:,0], pdots_d[:,1], color='white', linewidth=6, zorder=3)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)
plt.scatter(vpdots_d[:,0], vpdots_d[:,1], color=colors*5, marker='*', s=150, zorder=5)
plt.scatter(vdots[:,0], vdots[:,1], color=colors*5, s=150, zorder=6)
plt.grid(False)

Видно, что белая кривая прошла через каждую точку данных и слабо похожа на определяющую данные красную кривую: на лицо типичное переобучение.
Скрытые переменные
Можно рассмотреть генеральную совокупность как некоторый процесс генерации данных
- желаемой цифры,
- толщины штриха,
- наклона цифры,
- аккуратности,
- и т.д.
Каждый из этих факторов имеет свое априорное распределение, например, вероятность того, что будет нарисована восьмерка — это распределение Бернулли с вероятностью 1/10, толщина штриха тоже имеет некоторое свое распределение и может зависеть как от аккуратности, так и от своих скрытых переменных, таких как толщина ручки или темперамент человека (опять же со своими распределениями).
Автоэнкодер сам в процессе обучения должен прийти к скрытым факторам, например, таким как перечисленные выше, каким-то их сложным комбинациям, или вообще к совсем другим. Однако, то совместное распределение, которое он выучит, вовсе не обязано быть простым, это может быть какая-то сложная кривая область. (Декодеру можно передать и значения извне этой области, вот только результаты уже не будут из определяющего многообразия, а из его случайного непрерывного продолжения).
Именно поэтому мы не можем просто генерировать новые
Для определенности введем некоторые обозначения на примере цифр:
— случайная величина картинки 28х28,
— случайная величина скрытых факторов, определяющих цифру на картинке,
— вероятностное распределение изображений цифр на картинках, т.е. вероятность конкретного изображения цифры в принципе быть нарисованным (если картинка не похожа на цифру, то эта вероятность крайне мала),
— вероятностное распределение скрытых факторов, например, распределение толщины штриха,
— распределение вероятности скрытых факторов при заданной картинке (к одной и той же картинке могут привести различное сочетание скрытых переменных и шума),
— распределение вероятности картинок при заданных скрытых факторах, одни и те же факторы могут привести к разным картинкам (один и тот же человек в одних и тех же условиях не рисует абсолютно одинаковые цифры),
— совместное распределение
и
, наиболее полное понимание данных, необходимое для генерации новых объектов.
Посмотрим, как распределены скрытые переменные в обычном автоэнкодере:
Код
from keras.layers import Flatten, Reshape
from keras.regularizers import L1L2
def create_deep_sparse_ae(lambda_l1):
# Размерность кодированного представления
encoding_dim = 16
# Энкодер
input_img = Input(shape=(28, 28, 1))
flat_img = Flatten()(input_img)
x = Dense(encoding_dim*4, activation='relu')(flat_img)
x = Dense(encoding_dim*3, activation='relu')(x)
x = Dense(encoding_dim*2, activation='relu')(x)
encoded = Dense(encoding_dim, activation='linear', activity_regularizer=L1L2(lambda_l1, 0))(x)
# Декодер
input_encoded = Input(shape=(encoding_dim,))
x = Dense(encoding_dim*2, activation='relu')(input_encoded)
x = Dense(encoding_dim*3, activation='relu')(x)
x = Dense(encoding_dim*4, activation='relu')(x)
flat_decoded = Dense(28*28, activation='sigmoid')(x)
decoded = Reshape((28, 28, 1))(flat_decoded)
# Модели
encoder = Model(input_img, encoded, name="encoder")
decoder = Model(input_encoded, decoded, name="decoder")
autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
return encoder, decoder, autoencoder
encoder, decoder, autoencoder = create_deep_sparse_ae(0.)
autoencoder.compile(optimizer=Adam(0.0003), loss='binary_crossentropy')
autoencoder.fit(x_train, x_train,
epochs=100,
batch_size=64,
shuffle=True,
validation_data=(x_test, x_test))
n = 10
imgs = x_test[:n]
decoded_imgs = autoencoder.predict(imgs, batch_size=n)
plot_digits(imgs, decoded_imgs)
Вот так выглядят восстановленные этим энкодером изображения:
Изображения

Совместное распределение скрытых переменных
codes = encoder.predict(x_test)
sns.jointplot(codes[:,1], codes[:,3])

Видно, что совместное распределение
Есть ли какой-то способ контролировать распределения скрытых переменных
Самый простой способ — добавить регуляризатор
Регуляризатор вынуждает автоэнкодер искать скрытые переменные, которые распределены по нужным законам, получится ли у него — другой вопрос. Однако это никак не заставляет делать их независимыми, т.е.
Посмотрим на совместное распределение скрытых параметров в разреженом автоэнкодере.
Код и визуализация

s_encoder, s_decoder, s_autoencoder = create_deep_sparse_ae(0.00001)
s_autoencoder.compile(optimizer=Adam(0.0003), loss='binary_crossentropy')
s_autoencoder.fit(x_train, x_train, epochs=200, batch_size=256, shuffle=True,
validation_data=(x_test, x_test))
imgs = x_test[:n]
decoded_imgs = s_autoencoder.predict(imgs, batch_size=n)
plot_digits(imgs, decoded_imgs)
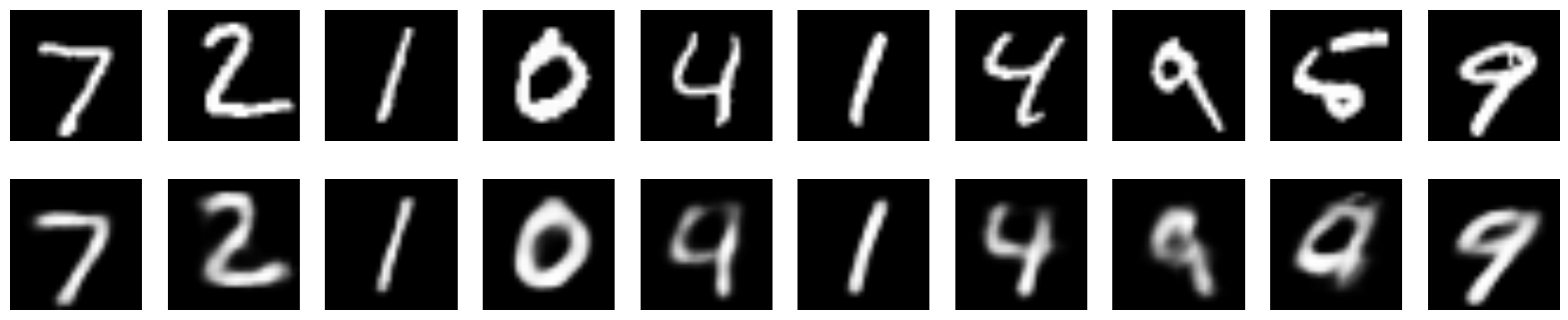
codes = s_encoder.predict(x_test)
snt.jointplot(codes[:,1], codes[:,3])

О том, как контролировать скрытое пространство, так, чтобы из него уже можно было осмысленно генерировать изображения — в следующей части про вариационные автоэнкодеры (VAE).
Полезные ссылки и литература
Этот пост основан на главе про автоэнкодеры (в частности подглавы Learning maifolds with autoencoders) в Deep Learning Book.