
Что такое бинарный поиск?
Когда нужно выполнить поиск в массиве, простейшим способом может быть использование indexOf() или, возможно, цикла for(). Любой из этих способов будет начинать перебирать массив начиная с начала и переходить по каждому элементу массива до тех пор, пока не будет найдено нужное значение.
Теперь сравним это с бинарным поиском.
Бинарный поиск позволяет выполнять поиск в отсортированном массиве путем многократного разбиения массива пополам.
Бинарный поиск выполняется путем проверки того, является ли искомое значение больше, меньше или равно среднему значению в нашем массиве:
- Если оно меньше, мы можем удалить правую половину массива.
- Если оно больше, мы можем удалить левую половину массива.
- Если оно равно, мы возвращаем значение
Но суть в том, что массив должен быть отсортирован, т. е. значения должны быть в правильном порядке чтобы бинарный поиск работал правильно.
При работе с большими объемами данных гораздо эффективнее использовать бинарный поиск, поскольку при каждой итерации удаляется половина ненужных значений массива, а не только одно неподходящее значение.
Проект
Недавно я опубликовал статью о том, как я написал интерактивный 30-дневный график цены bitcoin с API на React.
Одним из наиболее важных аспектов диаграммы является подсказка, отображающая соответствующие данные при наведении курсора на диаграмму. При перемещении мыши на подсказке обновляются данные из ближайшей точки диаграммы. Пример:
Как это работает?
У нас есть массив всех координат и соответствующих им данных. Координаты находятся внутри объекта, и каждый объект имеет svgX ключ. Выглядит это примерно так:
svgData = [
{svgX: 1367.844, data...},
{svgX: 1684.478, data...},
{svgX: 1168.474, data...},
{svgX: 1344.854, data...},
// etc.
]Изначально я использовал простой цикл for, чтобы сравнить текущую координату X курсора мыши со всеми значениями svgX в моем массиве данных.
Цикл
Вот как выглядит код цикла for. Мы перебираем все значения svgX, и объект со значением, которое ближе к координате X курсора мыши — это тот объект, данные которого мы хотим показать.
const {svgWidth} = this.props;
let closestPoint = {};
for(let i = 0, c = svgWidth; i < svgData.length; i++){
if ( Math.abs(svgData[i].svgX — this.state.hoverLoc) <= c ){
c = Math.abs(svgData[i].svgX — this.state.hoverLoc);
closestPoint = svgData[i];
}
}
Сначала мы получаем ширину нашего svg элемента и создаем пустой объект для хранения нашей ближайшей точки.
const {svgWidth} = this.props;
let closestPoint = {};Затем мы перебираем массив данных. Каждое svgX значение объекта в нашем массиве сравнивается с координатой X курсора мыши. Если текущая итерация цикла имеет значение ближе к курсору, чем любая другая итерация, то эта точка устанавливается как наша ближайшая точка.
При небольшом количестве данных этот метод является относительно быстрым. Однако, если у нас есть большой объем данных, этот вариант уже не будет таким эффективным.
Бинарный поиск
Ниже приведен пример кода бинарного поиска для поиска ближайшего значения:
const binarySearch = (data, target, start, end) => {
if(end < 1) return data[0];
const middle = Math.floor((start + (end - start)/2);
if (target == data[middle].svgX) return data[middle];
if (end — 1 === start) return Math.abs(data[start].svgX — target) > Math.abs(data[end].svgX — target) ? data[end] : data[start];
if (target > data[middle].svgX) return binarySearch(data,target,middle,end);
if (target < data[middle].svgX) return binarySearch(data,target,start,middle);
}
let closestPoint = binarySearch(data,target, 0, data.length-1)Нам нужно пять основных составляющих для нашего бинарного поиска:
- data — данные. Массив объектов.
- target — цель. Расположение курсора мыши (координата x).
- start — начало. Начальная позиция в массиве для текущей итерации бинарного поиска.
- еnd — конец. Конечная позиция в массиве для текущей итерации бинарного поиска.
- мiddle — середина. Середина массива для текущей итерации бинарного поиска.
Я знаю, что это немного запутанно, поэтому давайте рассмотрим пример, который упрощает приведенный выше код. В этом примере нашим целевым значением будет 3,7. Мы будем искать в массиве из пяти увеличивающихся чисел от 1 до 5.
Как видно из приведенного выше кода в строке 10, при запуске бинарного поиска мы передаем на вход весь массив данных, объект мыши, начальную позицию 0 и конечную позицию, равную полному размеру массива:
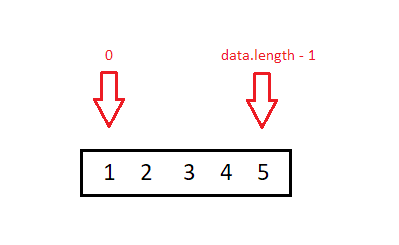
Когда у нас есть наши данные, середину массива найдем путем деления на два, суммы из начальной и конечной позиций. Чтобы не получить дробь, результирующее число округляется вниз:
const middle = Math.floor((start + (end - start)/2);Таким образом, середина 0 + (4-0)/2 округленная вниз = 2:
![Поиск среднего = data[2] Поиск среднего = data[2]](https://habrastorage.org/web/3e4/ce4/a5f/3e4ce4a5f41340389d543f5f8585d40c.png)
Мы помним, что для этого примера наше целевое значение равно 3,7. После того как мы нашли среднюю позицию, мы проверяем, равна ли она нашему целевому значению. Если это так, мы возвращаем объект, и все готово!
if (target == data[middle].svgX) return data[middle];К сожалению, среднее значение массива = 3. А нашей целью является 3,7.
Далее мы проверим, совпадает ли наша конечная позиция — 1, с нашей начальной позицией:
if (end — 1 === start) {
return Math.abs(data[start].svgX — target) > Math.abs(data[end].svgX — target) ? data[end] : data[start];
}
Это условие сработает, когда наш массив уменьшился до двух финальных значений, и наша цель находится между ними. В этом случае мы возвращаем ближнее значение.
На текущей итерации условие вернет false.
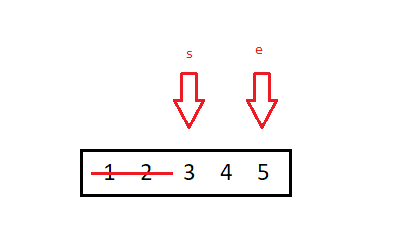
Далее мы проверяем, больше ли наше целевое значение за среднее:
if (target > data[middle].svgX) return binarySearch(data,target,middle,end);Это наш случай! Целевое значение 3,7 больше чем среднее 3. Мы можем избавиться от первых двух значений в нашем массиве:
Используя рекурсию мы возвращаем новый вызов функции binarySearch(). Передаем в функцию наш массив, целевое значение 3,7, среднее значение в качестве начальной позиции и конечное значение в качестве конечной позиции.
Наш новый вызов binarySearch(), будет искать от позиции 2 до data.length-1:

Функция находит новую среднюю позицию data[3]:
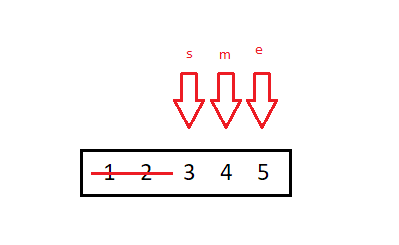
Поскольку наше целевое значение 3,7 меньше среднего значения 4, мы отбрасываем правую сторону массива и возвращаем новый вызов функции binarySearch(). На этот раз наша начальная позиция остается data[2], а конечная позиция меняется на среднюю data[3].
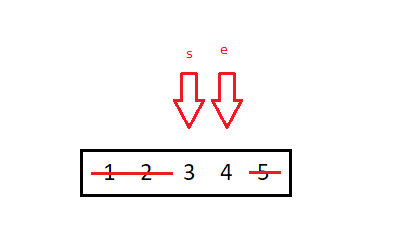
Мы дошли до момента, когда наше условие выполнится:
if (end — 1 === start) {
return Math.abs(data[start].svgX — target) > Math.abs(data[end].svgX — target) ? data[end] : data[start];
}Поскольку наше конечное значение минус единица равняется нашему начальному значению, мы знаем, что целевое значение находится где-то между ними. Мы должны возвратить элемент массива, значение которого ближе к значению 3,7. Поскольку 4 (конечное значение) ближе, то соответственно мы и возвращаем соответствующий элемент: data[3].
Тест скорости
Если объем данных небольшой, рекурсия может быть медленнее, чем цикл for. При тестировании на jsperf с 10 элементами, рекурсивная функция в среднем на 3% медленнее, чем цикл for. Однако при количестве элементов в 10 000, цикл for на 72% медленнее, чем рекурсивная функция. Это означает, что рекурсия практически в два раза быстрее, чем цикл for, и это огромная экономия времени!
Надеюсь, теперь вам понятны основы бинарного поиска в JavaScript!