Привет, Хабр!
Свой первый пост я решил посвятить квантовой информатике и ее приложению к теории игр. Эта идея абсолютна не нова и своими корнями уходит в статью Жиля Брассарда 1999 года [1]. Квантовая механика сама по себе удивительная вещь, а возможность ее использования в играх вдвойне удивляет!

Есть два игрока (назовем их Алиса и Боб), монетка и ящик. Перед началом игры кладем монетку в ящик орлом вверх. Алисе и Бобу завязывают глаза и начинается игра: первый ход за Алисой, второй — Боба, а третий ход снова Алисы. Каждый из игроков в свой ход может перевернуть монетку, либо оставить ее в прежнем состоянии (напоминаю, что игроки не видят какой стороной вверх лежит монетка). Если по окончанию третьего хода монетка лежит орлом вверх, то побеждает Алиса, если решкой — Боб.
Данная игра совсем простенькая, поэтому тут легко рассмотреть все варианты развития событий. Перебирать все исходы удобно в виде таблицы (подобная таблица в теории игр называется матрицей выигрышей).

Буквы «П» и «Н» соответствуют действиям игрока: перевернуть монетку и ничего не делать. В каждой ячейке таблицы указано имя победителя. Отсюда сразу видно, что вероятность выигрыша Алисы равна . К каким бы стратегиям не прибегали игроки, вероятность выигрыша каждого из них остается постоянной. И все бы хорошо, но Алиса оказалась очень азартным игроком: ей хочется выигрывать чаще чем в половине случаев! И квантовая механика способна помочь ей в этом!
. К каким бы стратегиям не прибегали игроки, вероятность выигрыша каждого из них остается постоянной. И все бы хорошо, но Алиса оказалась очень азартным игроком: ей хочется выигрывать чаще чем в половине случаев! И квантовая механика способна помочь ей в этом!
Для дальнейшего чтения желательно быть знакомым с основами квантовой механики и кубитологии. Товарищ devpony опубликовал пост в котором на качественном уровне все это объяснено. Так же можно почитать соответствующую литературу [2].
Давайте теперь представим, что у нас есть все тот же ящик, но внутри него лежит «квантовая монетка». В качестве этой монетки может выступать любая двухуровневая квантовая система (кубит): электрон со спином вверх/вниз, фотон с поляризацией по и против часовой стрелки или сверхпроводниковый кубит, состояние которого определяется направлением протекания тока. Вариантов огромное множество. Но мы будем работать с абстрактной моделью кубита, не зависящей от физической реализации. И тут играет крайне важную роль тот факт, что игроки не видят монетку. Наблюдение за состоянием монетки соответствует процедуре измерения, что убивает всю соль — возможность монетки находиться в состоянии суперпозиции орла и решки.
Введем два состояния для случаев «монета орлом вверх» и «монета решкой вверх»:
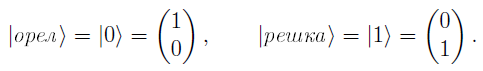
Теперь нужно определить квантовые операции, соответствующие классическим действиям игроков. Ну, тут все просто: переворачиванию монетки соответствует квантовый гейт NOT

который переводит состояние в
в  и наоборот. А действие «ничего не делать» соответствует тождественному преобразованию
и наоборот. А действие «ничего не делать» соответствует тождественному преобразованию
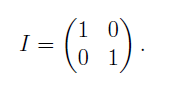
Будем считать, что Алиса внимательно слушала курс квантовой механики в институте и знает, что кроме этих двух преобразований (аналогичных классическим действиям), над кубитом можно выполнить любое преобразование, которое описывается унитарной матрицей. А Боб был тунеядцем, и считает, что квантовая механика ничем не отличается от классической, и над ней можно выполнять только две вышеупомянутые операции.
Алиса выбирает вентиль Адамара. Данный вентиль важен тем, что с его помощью можно создать суперпозицию состояний

На наши «монетные» состояние он действует следующим образом:

Последние обозначения введены для удобства дальнейшего использования.
Боб же с некоторой вероятностью (неизвестной для Алисы) выполняет одно из действий: или
или  . К сожалению подобное преобразование нельзя описать унитарной матрицей. Но теория открытых квантовых систем говорит нам, что подобное преобразование можно описать с помощью так называемых операторов Крауса [3]. Для дальнейшего рассмотрения нам потребуется представить наше состояние в виде матрицы плотности. Это более общая форма представления квантовых состояний, которая имеет очень широкое применение (подробнее почитать можно здесь [4]). Однако сейчас нам достаточно самого простого определения: если есть исходное состояние
. К сожалению подобное преобразование нельзя описать унитарной матрицей. Но теория открытых квантовых систем говорит нам, что подобное преобразование можно описать с помощью так называемых операторов Крауса [3]. Для дальнейшего рассмотрения нам потребуется представить наше состояние в виде матрицы плотности. Это более общая форма представления квантовых состояний, которая имеет очень широкое применение (подробнее почитать можно здесь [4]). Однако сейчас нам достаточно самого простого определения: если есть исходное состояние  , то соответствующая ему матрица плотности будет задаваться как
, то соответствующая ему матрица плотности будет задаваться как  . Это матрица размерности два с единичным следом и действительными неотрицательными собственными значениями (можете попробовать доказать эти два факта). Унитарная эволюция в терминах матриц плотности задается следующим образом
. Это матрица размерности два с единичным следом и действительными неотрицательными собственными значениями (можете попробовать доказать эти два факта). Унитарная эволюция в терминах матриц плотности задается следующим образом

Если же квантовое преобразование представлено операторами Крауса, то формула немного изменяется

где — операторы Крауса, удовлетворяющие условию разложения единицы
— операторы Крауса, удовлетворяющие условию разложения единицы
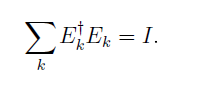 Легко видеть, что унитарная эволюция является частным случаем эволюции в терминах операторов Крауса (когда имеется всего одна компонента в сумме).
Легко видеть, что унитарная эволюция является частным случаем эволюции в терминах операторов Крауса (когда имеется всего одна компонента в сумме).
Возвращаемся к Бобу. Он с вероятностью переворачивает монетку, и соответственно, с вероятностью
переворачивает монетку, и соответственно, с вероятностью  не изменяет ее состояние. Это действие описывается двумя операторами Крауса:
не изменяет ее состояние. Это действие описывается двумя операторами Крауса:
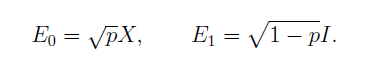
Взятие корня обусловлено необходимостью удовлетворить условию разложения единицы о котором шла речь выше.
Теперь у нас есть все необходимые инструменты для детального анализа этой игры. Давайте же наконец-то поиграем вместе с Алисой и Бобом!
По окончанию всех ходов монетка будет находиться в состоянии с вероятностью 1. Используя данный метод Алиса может побеждать во всех играх (до тех пор пока ей не встретится соперник, который также знает квантовую механику).
с вероятностью 1. Используя данный метод Алиса может побеждать во всех играх (до тех пор пока ей не встретится соперник, который также знает квантовую механику).
[1] G. Brassard, R. Cleve, A. Tapp «The cost of exactly simulating quantum entanglement with classical communication», 1999, arxiv.org/pdf/quant-ph/9901035.pdf.
[2] Дж. Прескилл «Квантовая информация и квантовые вычисления», 2008.
[3] Х.-П. Бройер, Ф. Петруччионе «Теория открытых квантовых систем», 2010.
[4] Нильсен М., Чанг И. «Квантовые вычисления и квантовая информация», 2006.
Свой первый пост я решил посвятить квантовой информатике и ее приложению к теории игр. Эта идея абсолютна не нова и своими корнями уходит в статью Жиля Брассарда 1999 года [1]. Квантовая механика сама по себе удивительная вещь, а возможность ее использования в играх вдвойне удивляет!

«Если квантовая механика вас не потрясла до глубины души, значит, вы ее еще не поняли.» (Нильс Бор)В этом посте речь пойдет о самой примитивной игре — подбрасывании монетки. Хотя вернее будет сказать переворачивании монетки. Суть игры в следующем:
Описание игры
Есть два игрока (назовем их Алиса и Боб), монетка и ящик. Перед началом игры кладем монетку в ящик орлом вверх. Алисе и Бобу завязывают глаза и начинается игра: первый ход за Алисой, второй — Боба, а третий ход снова Алисы. Каждый из игроков в свой ход может перевернуть монетку, либо оставить ее в прежнем состоянии (напоминаю, что игроки не видят какой стороной вверх лежит монетка). Если по окончанию третьего хода монетка лежит орлом вверх, то побеждает Алиса, если решкой — Боб.
Классический вариант
Данная игра совсем простенькая, поэтому тут легко рассмотреть все варианты развития событий. Перебирать все исходы удобно в виде таблицы (подобная таблица в теории игр называется матрицей выигрышей).

Буквы «П» и «Н» соответствуют действиям игрока: перевернуть монетку и ничего не делать. В каждой ячейке таблицы указано имя победителя. Отсюда сразу видно, что вероятность выигрыша Алисы равна
Для дальнейшего чтения желательно быть знакомым с основами квантовой механики и кубитологии. Товарищ devpony опубликовал пост в котором на качественном уровне все это объяснено. Так же можно почитать соответствующую литературу [2].
Квантовый вариант
Давайте теперь представим, что у нас есть все тот же ящик, но внутри него лежит «квантовая монетка». В качестве этой монетки может выступать любая двухуровневая квантовая система (кубит): электрон со спином вверх/вниз, фотон с поляризацией по и против часовой стрелки или сверхпроводниковый кубит, состояние которого определяется направлением протекания тока. Вариантов огромное множество. Но мы будем работать с абстрактной моделью кубита, не зависящей от физической реализации. И тут играет крайне важную роль тот факт, что игроки не видят монетку. Наблюдение за состоянием монетки соответствует процедуре измерения, что убивает всю соль — возможность монетки находиться в состоянии суперпозиции орла и решки.
Введем два состояния для случаев «монета орлом вверх» и «монета решкой вверх»:

Теперь нужно определить квантовые операции, соответствующие классическим действиям игроков. Ну, тут все просто: переворачиванию монетки соответствует квантовый гейт NOT

который переводит состояние

Будем считать, что Алиса внимательно слушала курс квантовой механики в институте и знает, что кроме этих двух преобразований (аналогичных классическим действиям), над кубитом можно выполнить любое преобразование, которое описывается унитарной матрицей. А Боб был тунеядцем, и считает, что квантовая механика ничем не отличается от классической, и над ней можно выполнять только две вышеупомянутые операции.
Алиса выбирает вентиль Адамара. Данный вентиль важен тем, что с его помощью можно создать суперпозицию состояний

На наши «монетные» состояние он действует следующим образом:

Последние обозначения введены для удобства дальнейшего использования.
Боб же с некоторой вероятностью (неизвестной для Алисы) выполняет одно из действий:

Если же квантовое преобразование представлено операторами Крауса, то формула немного изменяется

где

Возвращаемся к Бобу. Он с вероятностью

Взятие корня обусловлено необходимостью удовлетворить условию разложения единицы о котором шла речь выше.
Теперь у нас есть все необходимые инструменты для детального анализа этой игры. Давайте же наконец-то поиграем вместе с Алисой и Бобом!
- Ход 0) Монетка находится в ящике в состоянии
, соответствующая матрица плотности есть
.
- Ход 1) Первой ходит Алиса: она применяет преобразование Адмара

- Ход 2) Теперь очередь Боба, он с вероятностью
переворачивает монетку
Отдельно рассмотрим действие гейта NOT на состояние суперпозиции: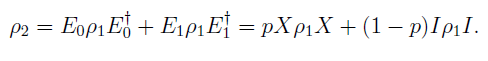
. Оказывается, оно его не изменяет, следовательно:
мы получили состояние, такое же, как после хода Алисы, то есть, ход Боба вообще ни на что не влияет! Именно этот факт позволяет Алисе выиграть в игре.
- Ход 3) Победный ход Алисы: применение оператора Адамара

По окончанию всех ходов монетка будет находиться в состоянии
Литература
[1] G. Brassard, R. Cleve, A. Tapp «The cost of exactly simulating quantum entanglement with classical communication», 1999, arxiv.org/pdf/quant-ph/9901035.pdf.
[2] Дж. Прескилл «Квантовая информация и квантовые вычисления», 2008.
[3] Х.-П. Бройер, Ф. Петруччионе «Теория открытых квантовых систем», 2010.
[4] Нильсен М., Чанг И. «Квантовые вычисления и квантовая информация», 2006.



