Введение
По линейному программированию средствами Python мною в статье [1] было рассмотрено решение задачи оптимизации с функцией цели альтернативной к основной. Как было показано в статье приём с введением новых функций цели при рассмотрении одной общей задачи оптимизации значительно расширяет аналитические возможности метода. Поэтому логично выбрать и рассмотреть такой пример, в котором при решении общей задачи оптимизации можно сформулировать несколько альтернативных функций цели.
Постановка задачи
На примере задачи об оптимальной диете рассмотреть формирование различных альтернативных функций цели с необходимыми начальными условиями. Кроме этого разработать простой и единообразный интерфейс решения подобных задач с выводом результатов понятных конечному пользователю.
Формирование целевой функции и начальных условий для минимизации стоимости диеты
Для поддержания нормальной жизнедеятельности человеку необходимо потреблять в день не менее 118 г белков, 56 г жиров, 500 г углеводов и 28 г минеральных солей. Эти питательные вещества содержатся в разных количествах и разных пищевых продуктах.
В таблице приведено количество питательных веществ в различных продуктах в г/кг и условная цена этих продуктов за 1 кг. Необходимо составить дневной рацион, содержащий минимальную суточную норму питательных веществ при минимальной их стоимости.
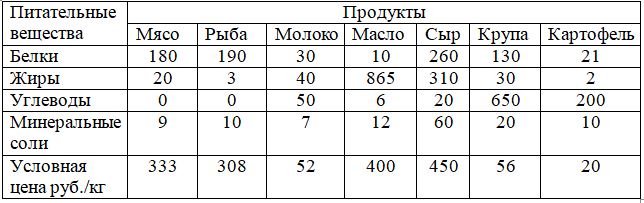
Обозначив через: Х1 –количество мяса; Х2- количество рыбы; Х3- количество молока; Х4- количество масла; Х5- количество сыра; Х6- количество крупы; Х7- количество картофеля, потребляемых человеком в день. Можем составить уравнение общей стоимости F питания в день:
F=333*X1+308*X2+52*X3+400*X4+450*X5+56*X6+25*X7
Нам нужно найти минимум F.
Суммарное количество белков в рационе человека должно быть не меньше 118 г. Отсюда:
180*X1+190*X2+30*X3+10*X4+260*X5+130*X6+21*X7≥118
Такие же неравенства составляем для жиров, углеводов и солей. Имеем:
20*X1+3*X2+40*X3+865*X4+310*X5+30*X6+2*X7≥56
50*X3+6*X4+20*X5+650*X6+200*X7≥500
9*X1+10*X2+7*X3+12*X4+60*X5+20*X6+10*X7≥28
Решим задачу
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(7, 'x')
z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6])
mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118)
mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56)
mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500)
mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative])
problem.solve(solver='glpk')
problem.status
print("Результат:")
print(round(1000*x.value[0],1),'-грамм мяса, затраты -',round(x.value[0]*333,1),'руб.')
print(round(1000*x.value[1],1),'-грамм рыбы, затраты -',round(x.value[1]*308,1),'руб.')
print(round(1000*x.value[2],1),'-миллилитров молока, затраты -',round(x.value[2]*52,1),'руб.')
print(round(1000*x.value[3],1),'-грамм масла, затраты -',round(x.value[3]*400,1),'руб.')
print(round(1000*x.value[4],1),'-грамм сыр, затраты -',round(x.value[4]*450,1),'руб.')
print(round(1000*x.value[5],1),'-грамм крупы, затраты -',round(x.value[5]*56,1),'руб.')
print(round(1000*x.value[6],1),'-грамм картофеля, затраты -',round(x.value[6]*25,1),'руб.')
print(round(problem.objective.value()[0],1),"- стоимость рациона одного человека в день")
stop = time.time()
print ("Время :",round(stop-start,3))
Следует отметить некоторые особенности написания программы с использованием модуля cvxopt. Modeling: все переменные сохраняются в списках, а индексы списков начинаются не с 1, а с 0; в условиях, которые записываются в виде нестрогих неравенств должно быть установлено ограничение сверху, поэтому, для перехода от ограничения снизу, обе части неравенств умножены на -1.
Результат:
0.0 -грамм мяса, затраты — 0.0 руб.
0.0 -грамм рыбы, затраты — 0.0 руб.
0.0 -миллилитров молока, затраты — 0.0 руб.
38.0 -грамм масла, затраты — 15.2 руб.
-0.0 -грамм сыр, затраты — -0.0 руб.
679.3 -грамм крупы, затраты — 38.0 руб.
1395.9 -грамм картофеля, затраты — 34.9 руб.
81.1 — стоимость рациона одного человека в день
Время: 0.09
Формирование целевой функции и начальных условий для минимизации калорийности диеты
Для определённости предположим, что в качестве исходных продуктов рассмотрим хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград – всего семь продуктов. В качестве питательных веществ – белки, жира, углеводы.
Калорийность одной весовой единицы каждого из продуктов следующая: c1=2060, c2=2430, c3=3600, c4=890, c5=140, c6=230, c7=650.
Содержание питательных веществ в продуктах питания поместим в следующую таблицу.
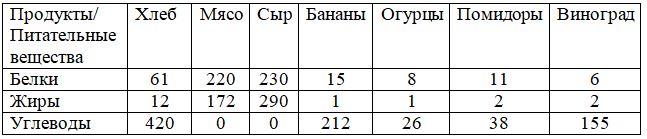
Минимальная суточная потребность человека в питательных веществах следующая: в белках b1=100, в жирах b2=70, в углеводах b3=400.
Не уменьшая общности решаемой задачи, можно считать, что калорийность продуктов измеряется в килокалориях/кг, суточная потребность в питательных веществах – в граммах, а содержание питательных веществ в продуктах– в граммах/кг. В указанных условиях становится возможным выполнить дополнительную проверку сформированных условий задачи на основе рассмотрения физической размерности целевой функции и ограничений.
Обозначив через: x1 –количество хлеба; x2- количество мяса; x3- количество сыра; x4- количество бананов; x5- количество огурцов; x6- количество помидоров; x7- количество винограда, потребляемых человеком в день в килограммах.
Можем составить уравнение общей калорийности F питания в день:
F=2060*x1 + 2430*x2 +3600* x3+890*x4 +140*x5 +230* x6+650*x7
Нам нужно найти минимум F.
Суммарное количество белков в рационе человека должно быть не меньше 100 г. Отсюда:
61*x1+ 220*x2 +230* x3 +15*x4 +8*x5 +11* x6+6*x7 ≥100
Такие же неравенства составляем для жиров и углеводов. Имеем:
12*x1 +172*x2 +290* x3+1*x4 +1*x5 +2* x6+2*x7 ≥70
420*x1 +0*x2 +0* x3 +212*x4+26*x5 +38* x6+155*x7 ≥400
Решим задачу
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(7, 'x')
z=(333*x[0] + 308*x[1] +52* x[2] +400*x[3] +450*x[4] +56* x[5]+20*x[6])
mass1 =(- (180*x[0] + 190*x[1] +30* x[2] +10*x[3] +260*x[4] +130* x[5]+21*x[6]) <= -118)
mass2 =(- (20*x[0] + 3*x[1] +40* x[2] +865*x[3] +310*x[4] +30* x[5]+2*x[6]) <= -56)
mass3 =(- (50* x[2] +6*x[3] +20*x[4] +650* x[5]+200*x[6]) <= -500)
mass4 =(- (9*x[0] + 10*x[1] +7* x[2] +12*x[3] +60*x[4] +20* x[5]+10*x[6]) <= -28)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3,mass4 ,x_non_negative])
problem.solve(solver='glpk')
problem.status
print("Результат:")
print(round(1000*x.value[0],1),'-грамм хлеба')
print(round(1000*x.value[1],1),'-грамм мяса')
print(round(1000*x.value[2],1),'-грамм сыра')
print(round(1000*x.value[3],1),'-грамм бананов')
print(round(1000*x.value[4],1),'-грамм огурцов')
print(round(1000*x.value[5],1),'-грамм помидоров')
print(round(1000*x.value[6],1),'-грамм винограда')
print(round(problem.objective.value()[0],1),"-Калорийность рациона одного человека в день")
stop = time.time()
print ("Время :",round(stop-start,3))Результат:
0.0 -грамм хлеба
211.5 -грамм мяса
109.4 -грамм сыра
1886.8 -грамм бананов
0.0 -грамм огурцов
0.0 -грамм помидоров
0.0 -грамм винограда
2587.1 -килокалорий -калорийность рациона одного человека в день
Время: 0.06
Формирование целевой функции и начальных условий для минимизации калорийности диеты при наборе продуктов по предпочтениям пользователя
Составляем условный набор продуктов, только для примера. Начальные условия для калорийности продуктов берём из решения предыдущей задачи.
Решение задачи
from cvxopt.modeling import variable, op
import time
start = time.time()
x = variable(7, 'x')
z=( x[0] + x[1] +x[2] +x[3] +x[4] +x[5]+x[6])
mass1 =(- (61*x[0] + 220*x[1] +230* x[2] +15*x[3] +8*x[4] +11* x[5]+6*x[6]) <= -100)
mass2 =(- (12*x[0] +172*x[1] +290* x[2] +1*x[3] +1*x[4] +2* x[5]+2*x[6]) <= -70)
mass3 =(- (420*x[0] +0*x[1] +0* x[2] +212*x[3] +26*x[4] +38* x[5]+155*x[6]) <= -400)
mass4 =(-( 2060*x[0] + 2430*x[1] +3600* x[2] +890*x[3] +140*x[4] +230* x[5]+650*x[6]) <= -3000)
x_non_negative = (x >= 0)
problem =op(z,[mass1,mass2,mass3, mass4,x_non_negative])
problem.solve(solver='glpk')
problem.status
print("Результат:")
print(round(1000*x.value[0],1),'-грамм хлеба')
print(round(1000*x.value[1],1),'-грамм мяса')
print(round(1000*x.value[2],1),'-грамм сыра')
print(round(1000*x.value[3],1),'-грамм бананов')
print(round(1000*x.value[4],1),'-грамм огурцов')
print(round(1000*x.value[5],1),'-грамм помидоров')
print(round(1000*x.value[6],1),'-грамм винограда')
print(round(problem.objective.value()[0],1),"-килограмм-общая масса продуктов из \n рациона одного человека в день")
stop = time.time()
print ("Время :",round(stop-start,3))Результат:
952.4 -грамм хлеба
0.0 -грамм мяса
288.4 -грамм сыра
0.0 -грамм бананов
0.0 -грамм огурцов
0.0 -грамм помидоров
0.0 -грамм винограда
1.2 -килограмм-общая масса продуктов из
рациона одного человека в день
Время: 0.051
Результаты решения задач в силу очевидности я не комментирую. Кроме того, исходные данные условны, а в последней задаче индивидуальны.
Практические выводы или зачем это всё нужно
Интерфейс программы настолько простой и наглядный, что не требует каких-либо дополнительных навыков. Достаточно скачать и установить последнюю версию Python, например, с сайта [2], а библиотеку cvxopt с сайта [3]. Затем создать файл с расширением py и поместить в него любую из приведенных в статье программ, предварительно модифицировав её под свою задачу с новой функцией цели и ограничениями.