Введение
Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1].
Постановка задачи
Получение простого, наглядного и общедоступного инструмента для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.
Теория просто и кратко
Анализ устойчивости системы по методу Михайлова сводится к построению характеристического многочлена замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):
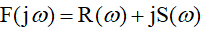 (1)
(1)где
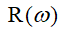 и
и 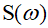 – соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.
– соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.Замкнутая САУ устойчива, если комплексная частотная функция
 , начинаясь на
, начинаясь на стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.
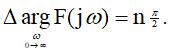 (2)
(2)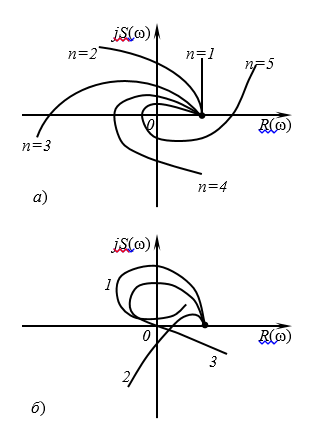
Рисунок 1. Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)
САУ электроприводом манипулятора промышленного робота (МПР)
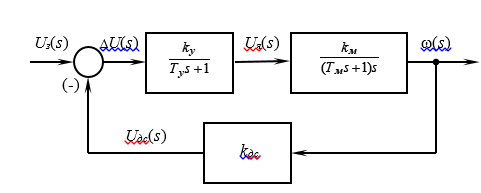
Рисунок 2 – Структурная схема САУ электроприводом МПР
Передаточная функция данной САУ имеет следующее выражение [2]:

где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи:
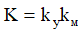 .
.Численные значения в выражение передаточной функции следующие:
K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.
Далее запишем характеристический многочлен замкнутой системы
 заменив s на
заменив s на 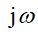 :
: (4)
(4)Решение на Python
Здесь следует отметить, что подобные задачи на Python ещё никто не решал, во всяком случае я не нашёл. Это было связано с ограниченными возможностями работы с комплексными числами. С появлением SymPy можно сделать следующее:
from sympy import *
T1,T2,w =symbols('T1 T2 w',real=True)
z=factor ((T1*w*I+1)*(T2*w*I+1)*w*I+1)
print ("Характеристический многочлен замкнутой системы -\n%s"%z)Где I мнимая единица, w- круговая частота, T1= Tу = 0.01 ,T2= Tм = 0.1
Получим развёрнутое выражение для многочлена:
Характеристический многочлен замкнутой системы –
-I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1
Сразу видим, что многочлен третьей степени. Теперь получим мнимую и действительную части в символьном отображении:
zr=re(z)
zm=im(z)
print("Действительная часть Re= %s"%zr)
print("Мнимая часть Im= %s"%zm)Получим:
Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w
Сразу видим вторую степень действительной части и третью мнимой. Подготовим данные для построения годографа Михайлова. Введём численные значения для T1 и T2, и будем менять частоту от 0 до 100 с шагом 0.1 и построим график:
from numpy import arange
import matplotlib.pyplot as plt
x=[zr.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)]
y=[zm.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)]
plt.plot(x, y)
plt.grid(True)
plt.show()
Из графика не видно, то годограф начинается на действительной положительной оси. Нужно изменить масштабы осей. Приведу полный листинг программы:
from sympy import *
from numpy import arange
import matplotlib.pyplot as plt
T1,T2,w =symbols('T1 T2 w',real=True)
z=factor((T1*w*I+1)*(T2*w*I+1)*w*I+1)
print("Характеристический многочлен замкнутой системы -\n%s"%z)
zr=re(z)
zm=im(z)
print("Действительная часть Re= %s"%zr)
print("Мнимая часть Im= %s"%zm)
x=[zr.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)]
y=[zm.subs({T1:0.01,T2:0.1,w:q}) for q in arange(0,100,0.1)]
plt.axis([-150.0, 10.0, -15.0, 15.0])
plt.plot(x, y)
plt.grid(True)
plt.show()Получим:
Характеристический многочлен замкнутой системы — -I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1
Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w
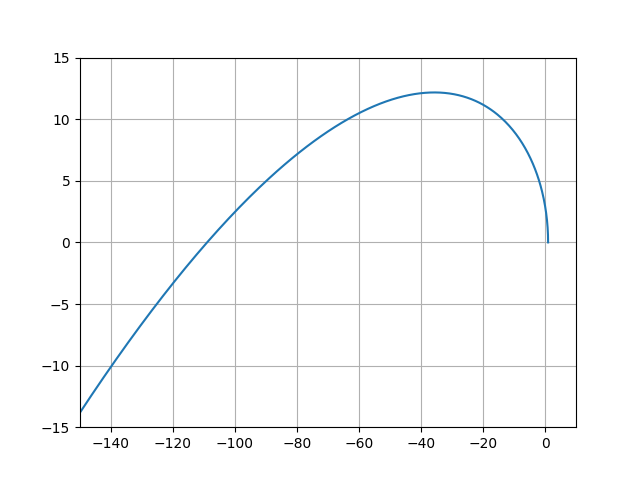
Теперь уже видно, что годограф начинается на действительной положительной оси. САУ устойчива, n=3, годограф совпадает с приведённым на первом рисунке.
Дополнительно убедится в том, что годограф начинается на действительной оси можно дополнив программу следующим кодом для w=0:
print("Начальная точка М(%s,%s)"%(zr.subs({T1:0.01,T2:0.1,w:0}),zm.subs({T1:0.01,T2:0.1,w:0})))Получим:
Начальная точка М(1,0)
САУ сварочного робота
Наконечник сварочного узла (НСУ) подводится к различным местам кузова автомобиля, быстро и точно совершает необходимые действия. Требуется определить устойчивость по критерию Михайлова САУ позиционированием НСУ.
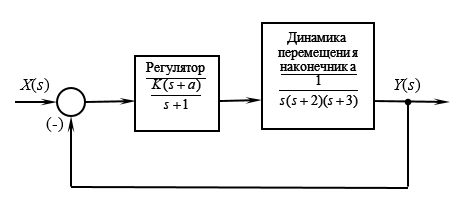
Рисунок 3. Структурная схема САУ позиционированием НСУ
Характеристическое уравнение данной САУ будет иметь вид [1]:
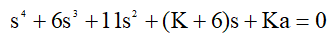
где K – варьируемый коэффициент усиления системы, a – определённая положительная константа. Численные значения: K = 40; a = 0,525.
Далее путём замены s на
 , получим функцию Михайлова:
, получим функцию Михайлова: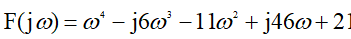 (5)
(5)Решение на Python
rom sympy import *
from numpy import arange
import matplotlib.pyplot as plt
w =symbols(' w',real=True)
z=w**4-I*6*w**3-11*w**2+I*46*w+21
print("Характеристический многочлен замкнутой системы -\n%s"%z)
zr=re(z)
zm=im(z)
print("Начальная точка М(%s,%s)"%(zr.subs({w:0}),zm.subs({w:0})))
print("Действительная часть Re= %s"%zr)
print("Мнимая часть Im= %s"%zm)
x=[zr.subs({w:q}) for q in arange(0,100,0.1)]
y=[zm.subs({w:q}) for q in arange(0,100,0.1)]
plt.axis([-10.0, 10.0, -50.0, 50.0])
plt.plot(x, y)
plt.grid(True)
plt.show()Получим:
Характеристический многочлен замкнутой системы — w**4 — 6*I*w**3 — 11*w**2 + 46*I*w + 21
Начальная точка М(21,0)
Действительная часть Re= w**4 — 11*w**2 + 21
Мнимая часть Im= -6*w**3 + 46*w
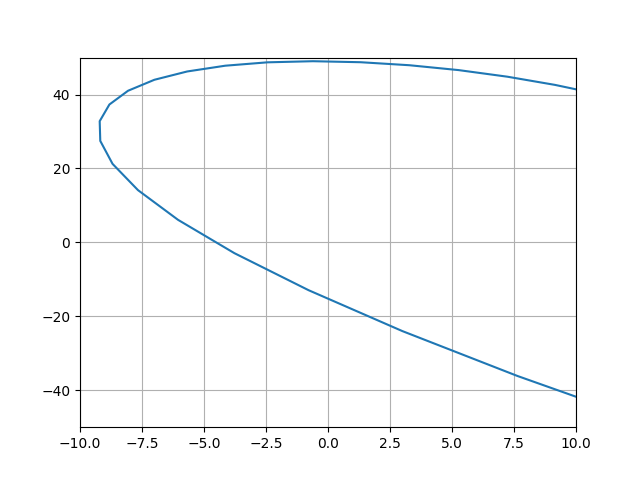
Построенный годограф Михайлова, начинаясь на вещественной положительной оси (М (21,0)), огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.
Выводы
При помощи модуля SymPy Python получен простой и наглядный инструмент для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.
Ссылки
- Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.
- Юревич Е.И. Основы робототехники 2-е издание / Е.И. Юревич. – С-Пб.: БХВ-Петербург, 2005. – 416 с.