Многомерная линейная регрессия — один из основополагающих методов машинного обучения. Несмотря на то, что современный мир интеллектуального анализа данных захвачен нейронными сетями и градиентным бустингом, линейные модели до сих пор занимают в нём своё почётное место.
В предыдущих публикациях на эту тему мы познакомились с тем, как получать точные оценки средних и ковариаций методом Уэлфорда, а затем научились применять эти оценки для решения задачи одномерной линейной регрессии. Конечно, эти же методы можно использовать и в задаче многомерной линейной регрессии.
Линейные модели часто используют благодаря нескольким очевидным преимуществам:
- высокая скорость обучения и применения;
- простота моделей, которая во многих случаях снижает риск переобучения;
- возможность построения композитных моделей с их использованием: скажем, имея много сотен тысяч факторов, можно обучить на них правильным образом несколько линейных моделей, предсказания которых затем использовать в качестве факторов для в более сложных алгоритмов — например, градиентного бустинга деревьев.
Кроме того, есть ещё одно классическое "преимущество" линейных моделей, о котором обычно говорят: интерпретируемость. На мой взгляд, оно несколько переоценено, однако очевидно, что определить, какой знак имеет коэффициент признака в линейной модели существенно проще, чем проследить его использование в огромной нейронной сети.
Содержание
- 1. Многомерная линейная регрессия
- 2. Общее описание решения
- 3. Применение метода Уэлфорда
- 4. Реализация
- 5. Экспериментальное сравнение методов
- Заключение
- Литература
1. Многомерная линейная регрессия
В задаче многомерной линейной регрессии требуется восстановить неизвестную зависимость наблюдаемой вещественной величины (которая является значением неизвестной целевой функции) от набора вещественных же признаков
.
Обычно для каждого отдельного наблюдения записываются значения признаков и целевой функции. Тогда из значений признаков для всех наблюдений можно составить матрицу признаков , а из значений целевой функции — вектор её значений
:
Здесь — некоторое конкретное наблюдение. Таким образом, строчки нашей матрицы соответствуют наблюдениям, а столбцы — признакам, а общее количество наблюдений и, следовательно, строк в матрице, —
.
Например, целевой функцией может быть значение температуры в конкретный день. Признаками — значения температуры в предшествующие дни в географически соседних точках. Другой пример — предсказание курса валюты или цены на акцию, в простейшем случае в качестве факторов опять же могут выступать значения той же величины в прошлом. Множество наблюдений формируется путём вычисления целевых значений и соответствующих им признаков в разные моменты времени.
Найти решение задачи означает построить некоторую решающую функцию . Сейчас мы говорим о задаче линейной регрессии, поэтому мы будем считать, что решающая функция является линейной. На самом деле, это значит, что решающая функция представляет из себя просто скалярное произведение вектора признаков на некоторый вектор весов:
Стало быть, решением нашей задачи является вектор весов признаков .
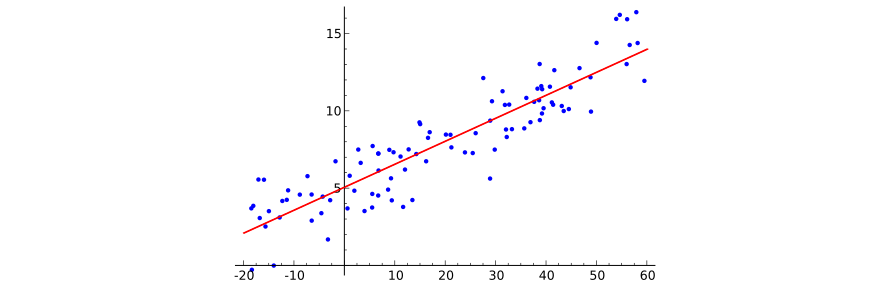
Изобразить многомерную линейную зависимость графически достаточно сложно (для начала, представим себе 100-мерное пространство признаков...), однако иллюстрации для одномерного случая вполне достаточно, чтобы понять происходящее. Позаимствуем эту иллюстрацию из Википедии:
Чтобы закончить формулировку задачи машинного обучения, требуется лишь указать функционал потерь, который отвечает на вопрос, насколько хорошо конкретная решающая функция предсказывает значения целевой функции. Сейчас мы будем использовать традиционный для регрессионного анализа среднеквадратический функционал потерь:
Итак, задачей многомерной линейной регрессии является нахождение набора весов такого, что значение функционала потерь
достигает на нём своего минимума.
Для анализа обычно удобно отказаться от радикала и усреднения в функционале потерь:
Для дальнейшего изложения будет удобно отождествить наблюдения с наборами соответствующих им факторов:
Нетрудно видеть, что функционал потерь теперь записывается просто как скалярный квадрат: вектор предсказаний можно записать как , а вектор отклонений от правильных ответов — как
. Тогда:
2. Общее описание решения
Из регрессионного анализа хорошо известно, что вектор-решение в задаче многомерной линейной регрессии находится как решение системы линейных алгебраических уравнений:
Получить доказательство этому несложно. Действительно, давайте рассмотрим частную производную функционала по весу
-го признака:
Если приравнять эту производную нулю, получим:
Теперь можно поменять порядок суммирования:
Теперь понятно, что коэффициент при слева — это соответствующий элемент матрицы
:
В свою очередь, правая часть построенного уравнения — это элемент вектора :
Соответственно, одновременное приравнивание нулю частных производных по всем компонентам решения приведёт к искомой системе линейных алгебраических уравнений.
3. Применение метода Уэлфорда
При решении СЛАУ возникают различные проблемы, например, мультиколлинеарность признаков, которая приводит к вырожденности матрицы
. Кроме того, необходимо выбрать метод для решения указанной СЛАУ.
Я не буду подробно останавливаться на этих вопросах. Скажу лишь, что в своей реализации я использую гребневую регрессию с адаптивным выбором коэффициента регуляризации, а для решения СЛАУ использую метод LDL-разложения.
Однако сейчас нас будет интересовать намного более приземлённая проблема: как сформировать уравнения для СЛАУ? Если эти уравнения сформированы корректно, а вычислительные погрешности невелики, можно надеяться, что выбранный метод приведёт к хорошему решению. Если же ошибки появились уже на этапе формирования матрицы системы и вектора в правой части, никакой метод решения СЛАУ не достигнет успеха.
Из сказанного выше ясно, что для составления СЛАУ необходимо вычислять коэффициенты двух типов:
Если бы выборка была центрированной, это были бы выражения для ковариаций, о которых говорили в самой первой статье!
С другой стороны, выборку можно центрировать самостоятельно. Пусть — матрица центрированной выборки, а
— вектор ответов для центрированной выборки:
Обозначим через среднее значение
-го признака, а через
— среднее значение целевой функции:
Пусть решением центрированной задачи является вектор коэффициентов . Тогда для
-го события величина предсказания будет вычисляться следующим образом:
При этом приближает центрированную величину. Отсюда можем окончательно записать решение исходной задачи:
Таким образом, коэффициенты линейной регрессии могут быть получены для центрированного случая, используя формулы вычисления средних и ковариаций по методу Уэлфорда. Затем они тривиальным образом преобразуются в решение для нецентрированного случая по выведенной сейчас формуле: коэффициенты всех признаков сохраняют свои значения, а вот свободный коэффициент вычисляется по формуле
4. Реализация
Реализацию методов многомерной линейной регрессии я поместил в ту же программу, о которой рассказывал в прошлый раз.
Когда впервые задумываешься о том, что фактически вся матрица метода многомерной линейной регрессии представляет собой большую ковариационную матрицу, очень хочется сделать каждый её элемент отдельной реализацией класса, реализующего вычисление ковариации. Однако это ведёт к неоправданным потерям в скорости: так, для каждого признака будет раз вычисляться среднее и сумма весов. Поэтому в результате раздумий родилась следующая реализация.
Решатель задачи многомерной линейной регрессии по методу Уэлфорда реализован в виде класса TWelfordLRSolver:
class TWelfordLRSolver {
protected:
double GoalsMean = 0.;
double GoalsDeviation = 0.;
std::vector<double> FeatureMeans;
std::vector<double> FeatureWeightedDeviationFromLastMean;
std::vector<double> FeatureDeviationFromNewMean;
std::vector<double> LinearizedOLSMatrix;
std::vector<double> OLSVector;
TKahanAccumulator SumWeights;
public:
void Add(const std::vector<double>& features, const double goal, const double weight = 1.);
TLinearModel Solve() const;
double SumSquaredErrors() const;
static const std::string Name() {
return "Welford LR";
}
protected:
bool PrepareMeans(const std::vector<double>& features, const double weight);
};Поскольку в процессе обновления величин ковариаций постоянно приходится иметь дело с разностями между текущим значением признака и его текущим средним, а также средним на следующем шаге, логично все эти величины вычислить заранее и сложить в несколько векторов. Поэтому класс содержит такое количество векторов.
При добавлении элемента первым делом вычисляются новый вектор средних значений признаков и величины отклонений.
Уже после этого обновляются элементы основной матрицы и вектора правых частей. От матрицы хранится только главная диагональ и один из треугольников, т.к. она симметрична.
Поскольку разности между текущими значениями факторов и их средними уже посчитаны и сохранены в специальном векторе, арифметически операция обновления матрицы оказывается достаточно простой:
Экономия на арифметических операциях здесь более чем оправдана, т.к. эта процедура обновления матрицы является наиболее затратной с т.з. ресурсов CPU с асимптотикой . Остальные операции, в т.ч. обновление вектора правых частей, асимптотически линейны:
Последний элемент, с реализацией которого надо разобраться — это формирование решающей функции. После того, как получено решение СЛАУ, осуществляется его преобразование к исходным, нецентрированным, признакам:
TLinearModel TWelfordLRSolver::Solve() const {
TLinearModel model;
model.Coefficients = NLinearRegressionInner::Solve(LinearizedOLSMatrix, OLSVector);
model.Intercept = GoalsMean;
const size_t featuresCount = OLSVector.size();
for (size_t featureNumber = 0; featureNumber < featuresCount; ++featureNumber) {
model.Intercept -= FeatureMeans[featureNumber] * model.Coefficients[featureNumber];
}
return model;
}5. Экспериментальное сравнение методов
Так же, как и в прошлый раз, реализации на основе метода Уэлфорда (welford_lr и normalized_welford_lr) сравниваются с "наивным" алгоритмом, в котором матрица и правая часть системы вычисляются по стандартным формулам (fast_lr).
Я использую тот же набор данных из коллекции LIAC, доступный в директории data. Используется такой же способ внесения шума в данные: значения признаков и ответов умножаются на некоторое число, после чего к ним прибавляется некоторое другое число. Таким образом мы можем получить проблемный с точки зрения вычислений случай: большие средние значения по сравнению с величинами разбросов.
В режиме research-lr выборка изменяется несколько раз подряд, и каждый раз на ней запускается процедура скользящего контроля. Результатом проверки является среднее значение коэффициента детерминации для тестовых выборок.
Например, для выборки kin8nm результаты работы получаются следующими:
linear_regression research-lr --features kin8nm.features
injure factor: 1
injure offset: 1
fast_lr time: 0.002304 R^2: 0.41231
welford_lr time: 0.003248 R^2: 0.41231
normalized_welford_lr time: 0.003958 R^2: 0.41231
injure factor: 0.1
injure offset: 10
fast_lr time: 0.00217 R^2: 0.41231
welford_lr time: 0.0032 R^2: 0.41231
normalized_welford_lr time: 0.00398 R^2: 0.41231
injure factor: 0.01
injure offset: 100
fast_lr time: 0.002164 R^2: -0.39518
welford_lr time: 0.003296 R^2: 0.41231
normalized_welford_lr time: 0.003846 R^2: 0.41231
injure factor: 0.001
injure offset: 1000
fast_lr time: 0.002166 R^2: -1.8496
welford_lr time: 0.003114 R^2: 0.41231
normalized_welford_lr time: 0.003978 R^2: 0.058884
injure factor: 0.0001
injure offset: 10000
fast_lr time: 0.002165 R^2: -521.47
welford_lr time: 0.003177 R^2: 0.41231
normalized_welford_lr time: 0.003931 R^2: 0.00013929
full learning time:
fast_lr 0.010969s
welford_lr 0.016035s
normalized_welford_lr 0.019693sТаким образом, даже относительно небольшая модификация выборки (масштабирование в сто раз с соответствующим сдвигом) приводит к неработоспособности стандартного метода.
При этом решение, основанное на методе Уэлфорда, оказывается весьма устойчивым к плохим данным. Среднее время работы методу Уэлфорда благодаря всем оптимизациям оказывается всего на 50% больше среднего времени работы стандартного метода.
Досадно лишь то, что "нормированный" метод Уэлфорда также работает плохо, и, кроме того, оказывается самым медленным.
Заключение
Сегодня мы научились решать задачу многомерной линейной регрессии, применять в ней метод Уэлфорда и убедились в том, что его использование позволяет достигать хорошей точности решений даже на "плохих" наборах данных.
Очевидно, если в вашей задаче требуется автоматически строить огромное количество линейных моделей и у вас нет возможности внимательно следить за качеством каждой из них, а дополнительное время исполнения не является определяющим, стоит использовать метод Уэлфорда как дающий более надёжные результаты.
Литература
- habrahabr.ru: Точное вычисление средних и ковариаций методом Уэлфорда
- habrahabr.ru: Метод Уэлфорда и одномерная линейная регрессия
- github.com: Linear regression problem solvers with different computation methods
- github.com: The collection of ARFF datasets of the Connectionist Artificial Intelligence Laboratory (LIAC)
- machinelearning.ru: Многомерная линейная регрессия