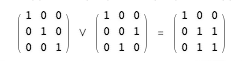Предлагаю вам сыграть в игру. Я даю вам квадратную сетку, на которой некоторые клетки закрашены, а некоторые могут остаться пустыми. Мы назовём её «шаблоном». Например, сетка может быть одним из таких шаблонов:

У вас есть стопка прозрачных пластмассовых листов, по размеру и форме совпадающих с сеткой, на которые нанесены узоры из чёрных точек:

Стоит заметить, что в каждом из этих узоров ровно по три точки, по одной точке в каждой строке и столбце. Шесть показанных комбинаций — это единственные сетки 3×3, обладающие таким свойством.
Ваша задача — собрать подмножество из прозрачных листов и наложить их на шаблон так, чтобы точки закрывали все закрашенные квадраты, но не попадали ни в один из пустых. Вы можете накладывать на любой из закрашенных квадратов несколько точек, но в целом нужно стремиться использовать как можно меньше листов. Чтобы было интереснее, я предлагаю сделать ставки: за правильное покрытие шаблона 3×3 я плачу 3 доллара, но вы должны мне заплатить по 1 доллару за каждый использованный лист. Выгодная ли это для вас ставка?
Прежде чем двинуться дальше, я должен сказать, что не каждый возможный шаблон можно закрыть в соответствии с такими правилами. Возьмём очевидный пример — никакой шаблон 3×3, в котором закрашено менее трёх квадратов, нельзя закрыть ни одной комбинацией из шести прозрачных листов с точками. Но я обещаю, что буду предлагать вам только шаблоны, которые можно закрыть некоторой комбинацией из имеющихся точечных узоров; если я ошибусь в этом, то потеряю поставленные деньги.
Какими будут результаты игры? Если я дам вам шаблон, помеченный выше как “1″, то вы запросто выиграете: достаточно выбрать сочетания a и b, которые закрывают только все закрашенные квадраты. Вы платите 2 доллара, а я даю вам 3. Шаблон 2, в котором закрашены все девять квадратов, может показаться самой сложной задачей. Очевидно, что его невозможно закрыть меньше, чем тремя листами с узорами, потому что в сумме нам нужно девять точек; и оказывается, что требуется ровно три листа. И в самом деле, существует два способа покрытия шаблона тремя листами: a + d + e и b + c + f. Таким образом, этот шаблон даёт нам безубыточное решение: вы зарабатываете 3 доллара и тратите 3 доллара.
Теперь мы перейдём к шаблону 3, в котором закрашенных квадратов и один пустой. Понятно, что если можно закрыть все девять квадратов всего тремя листами, то мы можем закрыть и восемь, правда? Рекомендую вам попробовать. На самом деле для единственного подходящего сочетания необходимо четыре листа: b + d + e + f. Поэтому моё предложение принимать не стоит: я всегда могу давать вам шаблон со всего одной пустым квадратом, а ваш убыток составит в целом 1 доллар.
Через секунду я вернусь к игровому столу, но для начала позвольте мне объяснить вам, откуда взялась эта задача. Когда-то я писал об «интервалах оценок», что привело меня к исследованию темы матриц перестановок. Повторю уже сказанное мной:
В комментариях Барри Ципра задаёт следующий вопрос:
Думаю, теперь вам очевидна связь между орматами и моей небольшой игрой. Шаблон из закрашенных и пустых квадратов является орматом; листы с точками обозначают матрицы перестановок; чтобы максимизировать свой выигрыш в игре (или минимизировать потери), вам нужно ответить на первый вопрос Барри, найдя минимальное количество перестановок, сочетание которых даст нам заданный ормат.
Для матриц 3×3 мы можем решить эту задачу поиском перебором, вычислив OR-суммы всех возможных комбинарий шести матриц перестановок 3×3 1, 2, 3, …, 6 одновременно. В недавнем авиаперелёте мне удалось это сделать с помощью бумаги и карандаша. В итоге я получил такие результаты:

Некоторые из чисел на этой карточке легко объяснить. Шесть орматов со всего тремя единичными элементами — это сами матрицы перестановок. Их шесть, потому что для трёх элементов возможно 3! = 6 перестановок. Орматов с четырьмя единичными элементами нет, и поразмыслив, это можно понять: не может быть перестановок, отличающихся друг от друга всего на один элемент. Если наложить друг на друга любые из шести показанных в начале статьи листов, то вы получите три, пять или шесть точек, но никогда четыре.
С другой стороны, нас не удивляет то, что существует ровно один ормат с девятью единичными элементами, и что для его создания требуется три перестановки. И существует девять орматов с восемью единичными элементами, требующие выполнения OR для четырёх перестановок. Это будут шаблоны с одним пустым квадратом, как показанный выше шаблон 3.
На основании этих результатов я начал размышлять о том, что же я получу при занесении в таблицу всех орматов 4×4.

Должно получиться 4! = 24 шаблонов с четырьмя единичными элементами, и всего один со всеми единицами, созданный из операцией OR над четырьмя перестановками. И должно быть 16 орматов, требующих пяти перестановок, а именно 16 матриц с единственным нулевым элементом. Последний прогноз показался мне менее очевидным, чем остальные.
Я рассуждал о случае с единственным нулём (или единственным пустым квадратом) примерно так: чтобы закрыть 15 квадратов множествами по четыре точек каждое, нам нужно не менее четырёх множеств, иначе нам просто не хватит точек. Поэтому полезной отправной точкой будет одна из оптимальных схем, закрывающая все 16 квадратов без пробелов и наложений. К этому моменту я подустал от рисования миллиардов точек, поэтому начал работать с монетами.

В этой схеме каждый номинал монеты образует перестановку: никакие две монеты в пенни, пять, десять или двадцать пять центов не находятся в одном столбце или в одной строке. Мы успешно закрыли все закрашенные квадраты, но, к сожалению, закрыли и один пустой в нижнем правом углу. Такая схема из монет не является приемлемым решением, но, возможно, мы можем это исправить?

Переместив пенни из пустого квадрата в другой квадрат того же столбца мы решаем одну проблему, но создаём другую: теперь схема расположения пенни больше не является перестановкой — в третьей строке находится два пенни.

То есть теперь мы должны сместить ещё одно пенни, чтобы восстановить свойство «одна монета на один столбец и строку». При этом закрашенный квадрат неизбежно останется открытым. Единственный способ, которым мы можем закрыть этот свободный квадрат — добавить пятую перестановку. У меня кончились номиналы монет, так что я использую популярный бренд тороидов для завтрака. Вуаля:

В перемещениях, сделанных мной для этой схемы, нет ничего необычного. Если попробовать другие шаблоны, то вы можете сами убедиться, что перемещение пенни, закрывающего пустой квадрат, в любой другой квадрат четвёртого столбца (или четвёртой строки) приведёт к точно такой же ситуации. Аналогично, результат игры будет тем же, если один пустой квадрат будет расположен в любом другом месте сетки. И вы можете также начать с другого множества исходных перестановок (при условии, что они закрывают все квадраты).
Это упражнение с перекладыванием монет показывает, что мы можем закрыть любой шаблон 4×4 с единственным пустым квадратом сочетанием не более пяти перестановок, но как мы узнаем, что нужно именно пять? Возможно, существует какая-то совершенно другая схема, которая справится всего с четырьмя перестановками? Давайте предположим, как может выглядеть такая схема. Она должна отличаться ровно в одной позиции от какой-то другой схемы перестановок, полностью закрывающей сетку из 16 квадратов. Но никакие две перестановки не могут отличаться в одной единственной точке. То есть рассуждение о том, что не может быть схемы из четырёх перестановок, закрывающей 15 квадратов, в сущности аналогично соображению о том, что никакой шаблон ормата 4×4 не может закрывать всего пять квадратов.
Этот аргумент можно обобщить до матриц k×k: для любого целого k должно существовать не менее k схем орматов, которые невозможно закрыть меньше, чем k+1 перестановками. Но затем мы можем сделать ещё больший скачок в рассуждениях: возможно, k+1 является верхней границей. Возможно, частью ответа на вопрос Барри является то, что ни для каких схем орматов k×k не требуется больше, чем k+1 перестановок. В какой-то момент у меня даже было «доказательство» этой гипотезы. Затем я написал программу, выполняющую примерно ту же работу, которую я проделывал с точками в самолёте.
Моя программа нашла 16 ожидаемых схем орматов, требующих пяти перестановок, но нашла и множество других. В общем она обнаружила 2 032 орматов 4×4, которые нельзя составить из менее чем пяти перестановок. Затем последовал большой сюрприз: программа также нашла 480 схем, требующих шести перестановок. Слишком много для моей предполагаемой верхней границы.
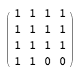
Один из этих 480 проблематичных орматов имеет такой вид:
Посмотрев на этот паттерн, я подумал, что понял причины ошибочности моих предыдущих рассуждений. Эта матрица точно такая же, как шаблон с одним нулём, только с двумя нулями! (Я действительно считаю, что это заявление имеет смысл. Следите за моими рассуждениями.) Допустим, мы начнём заново с множества из четырёх перестановок, полностью покрывающих всю сетку, в том числе и два пустых квадрата.

Затем мы можем открыть каждый пустой квадрат точно так же, как мы делали это с перестановкой монет, однако нам нужно быть аккуратными чтобы эти два множествами перемещений не влияли друг на друга. (Не очень много смысла в том, чтобы убирать с пустого квадрата пенни, а затем сразу класть туда пятицентовик.) Вот стратегия по открытию обоих пустых квадратов, сохраняющая свойство перестановки «один в столбце и строке»:

При открытии двух пустых квадратов мы неизбежно уберём монеты и с двух закрашенных квадратов, которые теперь снова нужно заполнить. Самое важное здесь то, что эту проблему не устранить никакой единственной перестановкой, потому что два открытых закрашенных квадрата находятся в одной строке. Чтобы закрыть оба этих квадрата, нам понадобится две дополнительные перестановки.
Другие способы перемещения монет избегают расположения двух открытых квадратов одном столбце или строке, но они всё равно проваливают все попытки выполнить полное покрытие всего пятью перестановками. Попробуйте добавить в показанную ниже схему четыре колечка. Если вы закроете оба открытых синих квадрата, то вы или закроете один из пустых квадратов, или два колечка окажутся в одной строке.

То есть нам теперь понятно, что для закрытия ормата 4×4 требуется шесть перестановок. Значит ли это, что верхняя граница в общем случае может быть равной k+2, а не k+1? А может быть, правильная формула — 2k–2? В поддержку последней гипотезы я предлагаю рассмотреть два следующих ормата, на которые требуются 8 и 10 перестановок соответственно:

Обманувшись несколько раз с верхней границей минимальных покрытий ормата, прежде чем предлагать ещё одну ставку, я хочу создать небольшое пространство для ошибок. У нас уже есть непосредственное свидетельство того, что на покрытие ормата k×k может потребоваться до 2k–2 перестановок. Поэтому я буду щедр и предложу вам 2k долларов за правильное покрытие, взымая по 1 доллару за каждую перестановку. Если k=3 или k=4, то вы точно можете заработать на этой сделке. Но будет ли она выгодной при бОльших k? (Подсказка: я бы сыграл в игру с такими правилами на живые деньги.)
Никто не согласен принять такую ставку? Жаль — я уже потратил свой выигрыш.
Барри Ципра, задавший вопрос о минимальном покрытии ормата, прислал мне замечательное письмо:
Определённо соответствует.
Во-первых, чтобы ответить на небольшой вопрос, который Барри оставил открытым, я покажу вам множество из 16 перестановок, которые успешно закрывают его «высокомерно-треугольную» матрицу 7×7:
Я обнаружил его простым жадным поиском.
Мои собственные попытки нахождения верхней границы были сосредоточены не на высокомерно-треугольных матрицах, а на матрицах, которые я называл «флагами», как вот этот пример для 7×7:

Для правильного покрытия этой матрицы также требуется 16 перестановок. Чтобы увидеть причины этого, попробуйте проводить перестановки через столбцы матрицы, начиная с левого края, выбирая в каждом столбце элемент 1 (и никогда не 0) из разных строк. Из-за блока нулей в верхнем левом углу первые три элемента каждой перестановки должны находиться в строках 4-7. То есть каждая перестановка «занимает» три из последних четырёх строк в первых трёх столбцах, а оставшаяся часть перестановки может снова попасть в этот интервал строк только один раз. Из этого следует, что каждая перестановка может касаться только одного элемента в блоке 4×4 из единичных элементов в правом нижнем углу матрицы, а для закрытия всех единичных элементов нужно не менее 16 перестановок. Доказать, что 16 перестановок достаточно, не так сложно.
Анализ такого вида работает для любых нечётных k, а поэтому мы знаем, что таким матрицам может потребоваться
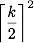
перестановок. (Для чётных k ситуация менее симметрична, и подробно я её не рассматривал.)
Эти результаты дают нам нижнюю границу в верхней границе количества перестановок, которые могут потребоваться для закрытия ормата k×k. Но мы не доказали, что это действительная верхняя граница. Существуют ли другие орматы, которым требуется ещё больше перестановок? Я считаю, что нет, но не забывайте, что почти все мои гипотезы, сделанные в этой статье, оказались неверными.

У вас есть стопка прозрачных пластмассовых листов, по размеру и форме совпадающих с сеткой, на которые нанесены узоры из чёрных точек:

Стоит заметить, что в каждом из этих узоров ровно по три точки, по одной точке в каждой строке и столбце. Шесть показанных комбинаций — это единственные сетки 3×3, обладающие таким свойством.
Ваша задача — собрать подмножество из прозрачных листов и наложить их на шаблон так, чтобы точки закрывали все закрашенные квадраты, но не попадали ни в один из пустых. Вы можете накладывать на любой из закрашенных квадратов несколько точек, но в целом нужно стремиться использовать как можно меньше листов. Чтобы было интереснее, я предлагаю сделать ставки: за правильное покрытие шаблона 3×3 я плачу 3 доллара, но вы должны мне заплатить по 1 доллару за каждый использованный лист. Выгодная ли это для вас ставка?
Прежде чем двинуться дальше, я должен сказать, что не каждый возможный шаблон можно закрыть в соответствии с такими правилами. Возьмём очевидный пример — никакой шаблон 3×3, в котором закрашено менее трёх квадратов, нельзя закрыть ни одной комбинацией из шести прозрачных листов с точками. Но я обещаю, что буду предлагать вам только шаблоны, которые можно закрыть некоторой комбинацией из имеющихся точечных узоров; если я ошибусь в этом, то потеряю поставленные деньги.
Какими будут результаты игры? Если я дам вам шаблон, помеченный выше как “1″, то вы запросто выиграете: достаточно выбрать сочетания a и b, которые закрывают только все закрашенные квадраты. Вы платите 2 доллара, а я даю вам 3. Шаблон 2, в котором закрашены все девять квадратов, может показаться самой сложной задачей. Очевидно, что его невозможно закрыть меньше, чем тремя листами с узорами, потому что в сумме нам нужно девять точек; и оказывается, что требуется ровно три листа. И в самом деле, существует два способа покрытия шаблона тремя листами: a + d + e и b + c + f. Таким образом, этот шаблон даёт нам безубыточное решение: вы зарабатываете 3 доллара и тратите 3 доллара.
Теперь мы перейдём к шаблону 3, в котором закрашенных квадратов и один пустой. Понятно, что если можно закрыть все девять квадратов всего тремя листами, то мы можем закрыть и восемь, правда? Рекомендую вам попробовать. На самом деле для единственного подходящего сочетания необходимо четыре листа: b + d + e + f. Поэтому моё предложение принимать не стоит: я всегда могу давать вам шаблон со всего одной пустым квадратом, а ваш убыток составит в целом 1 доллар.
Немного вводной информации
Через секунду я вернусь к игровому столу, но для начала позвольте мне объяснить вам, откуда взялась эта задача. Когда-то я писал об «интервалах оценок», что привело меня к исследованию темы матриц перестановок. Повторю уже сказанное мной:
- Матрица перестановок — это квадратная матрица с одной 1 в каждом столбце и каждой строке; остальные элементы равны 0.
- Ормат (ormat) — это суперпозиция матриц перестановок, сформированная применением булевой функции OR к соответствующим элементам матриц перестановок. Например:

- Не все квадратные матрицы с элементами (0,1) можно создать операциями OR над матрицами перестановок, но существует эффективный алгоритм определения того, является ли заданная матрица орматом.
- Общее количество путей перестановок в ормате, которые можно пропустить через единичные элементы матрицы, равно перманенту матрицы. Определение перманента считается сложной вычислительной задачей.
В комментариях Барри Ципра задаёт следующий вопрос:
Перманент сообщает нам максимальное количество различных перестановок, которые можно суммировать через OR для получения заданного ормата, но каким будет соответствующее минимальное количество? Кроме того, сколькими различными путями можно достичь минимума?
Думаю, теперь вам очевидна связь между орматами и моей небольшой игрой. Шаблон из закрашенных и пустых квадратов является орматом; листы с точками обозначают матрицы перестановок; чтобы максимизировать свой выигрыш в игре (или минимизировать потери), вам нужно ответить на первый вопрос Барри, найдя минимальное количество перестановок, сочетание которых даст нам заданный ормат.
Для матриц 3×3 мы можем решить эту задачу поиском перебором, вычислив OR-суммы всех возможных комбинарий шести матриц перестановок 3×3 1, 2, 3, …, 6 одновременно. В недавнем авиаперелёте мне удалось это сделать с помощью бумаги и карандаша. В итоге я получил такие результаты:

Некоторые из чисел на этой карточке легко объяснить. Шесть орматов со всего тремя единичными элементами — это сами матрицы перестановок. Их шесть, потому что для трёх элементов возможно 3! = 6 перестановок. Орматов с четырьмя единичными элементами нет, и поразмыслив, это можно понять: не может быть перестановок, отличающихся друг от друга всего на один элемент. Если наложить друг на друга любые из шести показанных в начале статьи листов, то вы получите три, пять или шесть точек, но никогда четыре.
С другой стороны, нас не удивляет то, что существует ровно один ормат с девятью единичными элементами, и что для его создания требуется три перестановки. И существует девять орматов с восемью единичными элементами, требующие выполнения OR для четырёх перестановок. Это будут шаблоны с одним пустым квадратом, как показанный выше шаблон 3.
На основании этих результатов я начал размышлять о том, что же я получу при занесении в таблицу всех орматов 4×4.

Должно получиться 4! = 24 шаблонов с четырьмя единичными элементами, и всего один со всеми единицами, созданный из операцией OR над четырьмя перестановками. И должно быть 16 орматов, требующих пяти перестановок, а именно 16 матриц с единственным нулевым элементом. Последний прогноз показался мне менее очевидным, чем остальные.
Мелочь из карманов и сухие завтраки
Я рассуждал о случае с единственным нулём (или единственным пустым квадратом) примерно так: чтобы закрыть 15 квадратов множествами по четыре точек каждое, нам нужно не менее четырёх множеств, иначе нам просто не хватит точек. Поэтому полезной отправной точкой будет одна из оптимальных схем, закрывающая все 16 квадратов без пробелов и наложений. К этому моменту я подустал от рисования миллиардов точек, поэтому начал работать с монетами.

В этой схеме каждый номинал монеты образует перестановку: никакие две монеты в пенни, пять, десять или двадцать пять центов не находятся в одном столбце или в одной строке. Мы успешно закрыли все закрашенные квадраты, но, к сожалению, закрыли и один пустой в нижнем правом углу. Такая схема из монет не является приемлемым решением, но, возможно, мы можем это исправить?

Переместив пенни из пустого квадрата в другой квадрат того же столбца мы решаем одну проблему, но создаём другую: теперь схема расположения пенни больше не является перестановкой — в третьей строке находится два пенни.

То есть теперь мы должны сместить ещё одно пенни, чтобы восстановить свойство «одна монета на один столбец и строку». При этом закрашенный квадрат неизбежно останется открытым. Единственный способ, которым мы можем закрыть этот свободный квадрат — добавить пятую перестановку. У меня кончились номиналы монет, так что я использую популярный бренд тороидов для завтрака. Вуаля:

В перемещениях, сделанных мной для этой схемы, нет ничего необычного. Если попробовать другие шаблоны, то вы можете сами убедиться, что перемещение пенни, закрывающего пустой квадрат, в любой другой квадрат четвёртого столбца (или четвёртой строки) приведёт к точно такой же ситуации. Аналогично, результат игры будет тем же, если один пустой квадрат будет расположен в любом другом месте сетки. И вы можете также начать с другого множества исходных перестановок (при условии, что они закрывают все квадраты).
Это упражнение с перекладыванием монет показывает, что мы можем закрыть любой шаблон 4×4 с единственным пустым квадратом сочетанием не более пяти перестановок, но как мы узнаем, что нужно именно пять? Возможно, существует какая-то совершенно другая схема, которая справится всего с четырьмя перестановками? Давайте предположим, как может выглядеть такая схема. Она должна отличаться ровно в одной позиции от какой-то другой схемы перестановок, полностью закрывающей сетку из 16 квадратов. Но никакие две перестановки не могут отличаться в одной единственной точке. То есть рассуждение о том, что не может быть схемы из четырёх перестановок, закрывающей 15 квадратов, в сущности аналогично соображению о том, что никакой шаблон ормата 4×4 не может закрывать всего пять квадратов.
Этот аргумент можно обобщить до матриц k×k: для любого целого k должно существовать не менее k схем орматов, которые невозможно закрыть меньше, чем k+1 перестановками. Но затем мы можем сделать ещё больший скачок в рассуждениях: возможно, k+1 является верхней границей. Возможно, частью ответа на вопрос Барри является то, что ни для каких схем орматов k×k не требуется больше, чем k+1 перестановок. В какой-то момент у меня даже было «доказательство» этой гипотезы. Затем я написал программу, выполняющую примерно ту же работу, которую я проделывал с точками в самолёте.
Вышли за границы
Моя программа нашла 16 ожидаемых схем орматов, требующих пяти перестановок, но нашла и множество других. В общем она обнаружила 2 032 орматов 4×4, которые нельзя составить из менее чем пяти перестановок. Затем последовал большой сюрприз: программа также нашла 480 схем, требующих шести перестановок. Слишком много для моей предполагаемой верхней границы.
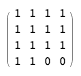
Один из этих 480 проблематичных орматов имеет такой вид:
Посмотрев на этот паттерн, я подумал, что понял причины ошибочности моих предыдущих рассуждений. Эта матрица точно такая же, как шаблон с одним нулём, только с двумя нулями! (Я действительно считаю, что это заявление имеет смысл. Следите за моими рассуждениями.) Допустим, мы начнём заново с множества из четырёх перестановок, полностью покрывающих всю сетку, в том числе и два пустых квадрата.

Затем мы можем открыть каждый пустой квадрат точно так же, как мы делали это с перестановкой монет, однако нам нужно быть аккуратными чтобы эти два множествами перемещений не влияли друг на друга. (Не очень много смысла в том, чтобы убирать с пустого квадрата пенни, а затем сразу класть туда пятицентовик.) Вот стратегия по открытию обоих пустых квадратов, сохраняющая свойство перестановки «один в столбце и строке»:

При открытии двух пустых квадратов мы неизбежно уберём монеты и с двух закрашенных квадратов, которые теперь снова нужно заполнить. Самое важное здесь то, что эту проблему не устранить никакой единственной перестановкой, потому что два открытых закрашенных квадрата находятся в одной строке. Чтобы закрыть оба этих квадрата, нам понадобится две дополнительные перестановки.
Другие способы перемещения монет избегают расположения двух открытых квадратов одном столбце или строке, но они всё равно проваливают все попытки выполнить полное покрытие всего пятью перестановками. Попробуйте добавить в показанную ниже схему четыре колечка. Если вы закроете оба открытых синих квадрата, то вы или закроете один из пустых квадратов, или два колечка окажутся в одной строке.

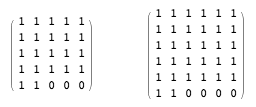
То есть нам теперь понятно, что для закрытия ормата 4×4 требуется шесть перестановок. Значит ли это, что верхняя граница в общем случае может быть равной k+2, а не k+1? А может быть, правильная формула — 2k–2? В поддержку последней гипотезы я предлагаю рассмотреть два следующих ормата, на которые требуются 8 и 10 перестановок соответственно:
Ещё одна ставка
Обманувшись несколько раз с верхней границей минимальных покрытий ормата, прежде чем предлагать ещё одну ставку, я хочу создать небольшое пространство для ошибок. У нас уже есть непосредственное свидетельство того, что на покрытие ормата k×k может потребоваться до 2k–2 перестановок. Поэтому я буду щедр и предложу вам 2k долларов за правильное покрытие, взымая по 1 доллару за каждую перестановку. Если k=3 или k=4, то вы точно можете заработать на этой сделке. Но будет ли она выгодной при бОльших k? (Подсказка: я бы сыграл в игру с такими правилами на живые деньги.)
Никто не согласен принять такую ставку? Жаль — я уже потратил свой выигрыш.
Барри Ципра, задавший вопрос о минимальном покрытии ормата, прислал мне замечательное письмо:
Я дам наметки на краткий путь к гипотезе (на самом деле, всего лишь к догадке), что поведение в «наихудшем случае», с точки зрения минимального количества перестановок, необходимых для получения заданного ормата, возникает для орматов следующего вида, показанного здесь для k=7:
Чтобы не нарушать существующую терминологию матриц, я буду называть любую (квадратную) матрицу такого типа, т.е. такую, все элементы которой ниже основной поддиагонали равны 0, «высокомерно-треугольной». Я могу показать (и сделаю это!), что этот высокомерно-треугольный ормат при k=7 требует (не менее) 16 перестановок, и что начиная с этого значения k количество резко возрастает. Поэтому лично я точно не стал бы принимать вашу ставку в 2k долларов.
Хитрость заключается в том, чтобы рассматривать каждый ормат как «тень» того, что я буду называть «аддматом» (addmat). Пусть P1, P2, …, Pr будут матрицами перестановок k×k; тогда их аддматом будет обычный результат сложения: S = P1 + P2 + … + Pr, элементами которого являются положительные целые числа, где одна или более составляющих перестановок имеют 1, в противном случае они являются нулём. Соответствующий ормат получается заменой каждого из ненулевых элементов на 1 с сохранением нулевых элементов. В этом смысле, единичные элементы ормата являются «тенями» положительных элементов адмата.
Самое важное заключается в том, что у аддматов есть приятное небольшое свойство, которого не имеет его тень: все суммы строки и столбца элементов аддмата равны количеству создавших их перестановок r.
А теперь давайте поразмышляем вместе. Представленный выше пример высокомерно-треугольного ормата (при k=7) должен получаться из аддмата вида
где a, b и все * являются положительными числами. В частности, каждая * имеет значение не меньше 1. Поскольку все суммы строк и столбцов должны быть одинаковыми, то сумма a+b должна быть равна b и всем шести * над ними. Следовательно, a имеет значение не меньше 6. Аналогично, сумма a+b должна равняться сумме a и всех шести * над ней, то есть значение b тоже не меньше 6. Следовательно, a+b не меньше 12, то есть OR-сумма, создающая заданный ормат, требует не менее 12 перестановок.
Эти рассуждения можно обобщить до произвольного k, то есть мы получаем не просто «непосредственное свидетельство» того, что для ормата k×k может потребоваться до 2k–2 перестановок — это строгое доказательство! Но мы можем сразу же улучшить его, по крайней мере, для конкретных случаев. Если мы попробуем обойтись всего 12 перестановками для этого высокомерно-треугольного ормата, то у нас быстро возникнет проблема. Очевидно, что нам потребуется a = b = 6, а, следовательно, все * над ними являются единицами (чтобы получить в этом столбце сумму 12). То есть у нас получился аддмат
в котором я хочу привлечь ваше внимание к элементу, помеченному как "@". Чтобы сделать сумму его строки равной 12, нам нужно, чтобы @ = 10. Но это значит, что сумма его столбца (с пятью * над ним) не меньше 15. Но такого не может быть! Значит, нам приходиться пробовать подобрать бОльшие значения a и/или b, то есть для создания этого аддмата нам нужно больше матриц перестановок.
Оказывается, мы не можем удовлетворить условие сумм строк и столбцов, пока мы не доберёмся до a = b = 8. Я не буду объяснять все этапы, а просто покажу предпоследнее возможное сочетание, a = 7, b = 8. Лучшее, на что можно надеяться в этом случае:
Заметьте, что в последних двух столбцах я придал как можно «веса», чтобы они как можно ближе были к 7 и 8, и можно было использовать наименьшее возможное значение (10) в качестве элемента с пятью положительными элементами над ним. Благодаря этому последние три строки и три правые строки имеют одинаковую сумму (15), но теперь появилась проблема у столбца с элементом 12: его сумма не меньше 16. Так что, повторюсь, мы в тупике. Мы можем избежать противоречия только при следующей попытке:
Наконец-то все суммы строк и столбцов матрицы одинаковы. Стоит учесть, что это может быть, а может и не быть настоящим аддматом множества 16 матриц перестановок. Подозреваю, что это всё-таки аддмат, но не хочу это проверять. Всё, что мы знаем — он удовлетворяет необходимому условию аддмата, а именно — все суммы строк и столбцов одинаковы. (Было бы здорово, если бы это было достаточным условием, но что-то подсказывает мне, что это не так.)
Этот пример, который точно можно воспроизвести при бОльших значениях k, даёт нам понять, что предлагающий игру находится в выигрыше не только при ставке 2k долларов. но и при (2k+2) долларов и выше. Я немного поэкспериментировал с этим и убедился, что количество матриц перестановок будет намного больше 2k при k=10. Если я всё сделал правильно, то вам понадобится 24 перестановок (а возможно и больше, если анализ высокомерно-треугольной матрицы покажет нам, что она не является настоящим аддматом). Я абсолютно убеждён, что после внимательных размышлений можно упростить анализ до удобного и изящного доказательства. Я просто не уверен, не сделал ли я уже ошибки и не построил ли карточный домик из рассуждений.
Соответствует ли всё сказанное тому, к чему пришли вы?
Определённо соответствует.
Во-первых, чтобы ответить на небольшой вопрос, который Барри оставил открытым, я покажу вам множество из 16 перестановок, которые успешно закрывают его «высокомерно-треугольную» матрицу 7×7:
{1,2,3,4,5,6,7} {2,1,4,3,6,7,5} {1,3,2,5,4,7,6} {1,3,4,2,6,5,7}
{2,3,1,5,6,4,7} {1,2,3,5,6,7,4} {1,2,4,5,3,6,7} {1,2,4,5,6,3,7}
{1,2,4,5,6,7,3} {1,3,4,5,2,6,7} {1,3,4,5,6,2,7} {1,3,4,5,6,7,2}
{2,3,4,1,5,6,7} {2,3,4,5,1,6,7} {2,3,4,5,6,1,7} {2,3,4,5,6,7,1}Я обнаружил его простым жадным поиском.
Мои собственные попытки нахождения верхней границы были сосредоточены не на высокомерно-треугольных матрицах, а на матрицах, которые я называл «флагами», как вот этот пример для 7×7:

Для правильного покрытия этой матрицы также требуется 16 перестановок. Чтобы увидеть причины этого, попробуйте проводить перестановки через столбцы матрицы, начиная с левого края, выбирая в каждом столбце элемент 1 (и никогда не 0) из разных строк. Из-за блока нулей в верхнем левом углу первые три элемента каждой перестановки должны находиться в строках 4-7. То есть каждая перестановка «занимает» три из последних четырёх строк в первых трёх столбцах, а оставшаяся часть перестановки может снова попасть в этот интервал строк только один раз. Из этого следует, что каждая перестановка может касаться только одного элемента в блоке 4×4 из единичных элементов в правом нижнем углу матрицы, а для закрытия всех единичных элементов нужно не менее 16 перестановок. Доказать, что 16 перестановок достаточно, не так сложно.
Анализ такого вида работает для любых нечётных k, а поэтому мы знаем, что таким матрицам может потребоваться
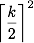
перестановок. (Для чётных k ситуация менее симметрична, и подробно я её не рассматривал.)
Эти результаты дают нам нижнюю границу в верхней границе количества перестановок, которые могут потребоваться для закрытия ормата k×k. Но мы не доказали, что это действительная верхняя граница. Существуют ли другие орматы, которым требуется ещё больше перестановок? Я считаю, что нет, но не забывайте, что почти все мои гипотезы, сделанные в этой статье, оказались неверными.