Темой сегодняшней статьи будут классы типов, некоторые стандартные из них, синтаксический сахар с их использованием и класс монад.
Классы привносят динамический полиморфизм, как и интерфейсы в традиционных императивных языках, а также могут быть использованы как замены отсутствующей в Хаскеле перегрузки функций.
Я расскажу, как определить класс типов, его экземпляры (instance) и как это всё устроено внутри.
Предыдущие статьи:
Типы данных, паттернг матчинг и функции
Основы
Предположим, вы написали свой тип данных и хотите написать для него оператор сравнения. Проблема в том, что перегрузки функций в Хаскеле нет и потому использовать для этих целей (==) простым способом не получится. Более того, придумывать для каждого типа новое имя — не вариант.
Но вы можете определить класс типов «сравниваемый». Тогда, если ваш тип данных принадлежит к этому классу, значения этого типа можно будет сравнивать.
Тип
В классе можно дать определение функции по умолчанию. Например, функции
Теперь напишем экземпляр класса для
Определяем одну функцию
Такие же ограничения можно накладывать и при объявлении самого класса:
Классы чем-то похожи на интерфейсы — мы объявляем фукнции, для которых потом предоставляем реализации. Другие функции могут использовать эти функции только если для некоторого типа есть такая реализация.
Однако есть существенные отличия как в возможностях, так и в реализации самого механизма.
Раз уж упомянул C++, то заодно скажу, что в новом стандарте C++0x concept и concept_map есть суть классы типов, но используемые на этапе компиляции :)
Но есть и недостаток. Как нам завести список объектов, которые, к примеру, принадлежат к классу
Способ есть, но он нестандартен. В начало файла необходимо добавить соответствующие опции GHC:
И заодно определить для него экземляр класса
В функцию, которая накладывает ограничения на тип, передаётся скрытый параметр (на каждый класс и тип — свой) — словарь со всеми необходимыми функциями.
Фактически,
Чтобы было проще это понять, я просто приведу псевдо-реализацию для класса
Enum — перечисление. Определяет функции для получение следующего/предыдущего значения, а также значения по номеру.
Используется в синтаксическом сахаре для списков
Show — преобразование в строку, основная функция
Используется, например, интерпретатором для вывода значений.
Read — преобразование из строки, основная функция
Не знаю, почему выбрали возвращение значения, а не
Eq — сравнение, операторы
Ord — упорядоченные типы, операторы
Более полный список различных классов можно посмотреть здесь.
Functor — функтор, функция
Чтобы было понятно, приведу примеры применения этой функции:
Подробнее про ввод-вывод я напишу далее, сейчас можно просто запомнить, что
Чтобы каждый раз не определять экземпляры для вновь написанных типов данных, Haskell умеет делать это автоматически для некоторых классов.
Класс Monad представляет собой «вычисление», т.е. он позволяет описывать способ комбинирования вычислений и результатов.
Вряд ли я напишу статью лучше, чем есть уже написанные, так что я просто дам ссылки на лучшие (по моему мнению) статьи для понимания, для чего эти монады нужны.
1. Монады — статья с SPbHUG о монадах на русском языке и с аналогиями на привычных императивных языках.
2. IO inside — статья на английском о вводе-выводе с использованием монад
3. Yet Another Haskell Tutorial — книга по Хаскелю, в разделе Monads очень хорошо написано на примере создания класса Computation, который суть и есть монада.
Здесь я напишу очень вкратце, чтобы можно было потом подглядеть.
Допутим, мы хотим описать последовательные вычисления, где каждое следующее зависит от результатов предыдущего (некоторым не заданным наперёд способом). Для этого можно определить соответствующий класс, в котором должны быть как минимум две функции:
Вторая функция принимает 2 аргумента:
1. вычисление, которое при выполнении вернёт значение типа
2. функцию, которое примет значение типа
Результатом будет вычисление, которое вернёт значение типа
Зачем всё это может быть нужно, я покажу на примере опционального значения
Но ведь у нас язык позволяет передавать функции в качестве аргументов и возвращать так же, воспользуемся:
Перепишем функцию
Можно заметит, что тип функции
Кроме того, для монад определён синтаксический сахар, который значительно упрощает их использование:
Специальный синтаксис с обратной стрелкой
1. do {e} -> e
do с одним вычислением есть само это вычисление, комбинировать ничего не нужно
2. do {e; es} -> e >> do {es}
несколько подряд идущих вычислений соединяются оператором
3. do {let decls; es} -> let decls in do {es}
внутри do можно заводить дополнительные декларации наподобие
4. do {p < — e; es} -> let ok p = do {es}; ok _ = fail "..." in e >>= ok
если результат первого вычисления используется в дальнейшем, то для комбинации используется оператор
В последнем случае такая конструкция используется потому, что в качестве
Если он совпадёт, то будет выполнено дальшейшее вычисление, в противном случае будет возвращена ошибка со строковым описанием.
Функция
Какие ещё экземпляры монад есть в стандартной библиотеке?
State — вычисления с состоянием. При помощи функций
Список — тоже монада. Последующие вычисления применяются ко всем результатам предыдущего.
Continuations (продолжения) в Хаскеле — тоже монада — Cont
Про продолжения можно почитать на русской вики и английской вики и далее по ссылкам.
Они заслуживают отдельного внимания, но всё я не умещу, да и к монадам они непосредственного отношения не имеют.
Хорошая статья про продолжения в Scheme есть у пользователя palm_mute в живом журнале.
Ввод-вывод тоже реализован с использованием монады. Например, тип функции
т.е. любая функция ввода-вывода как бы принимает состояние мира, а возвращает некоторый результат и новое состояние мира, которое затем используется последующими функциями.
Разумеется, это всего лишь мысленное представление.
Так как в отличие от списков и Maybe у нас нет конструкторов типа
(«Никогда» — это громко сказано, на самом деле есть
Стоит упомянуть Monad transformers (трансформаторы монад).
Если нам нужно состояние, мы можем использовать
Для этого предназначен трансформер StateT, который соединяет
Посмотрим на примере факториала, который мы изменим так, чтобы он печатал аккумулятор
Кроме StateT есть также ListT (для списка).
Полный список монад и трансформеров монад.
Для удобства над монадами определены обобщённые функции. Их названия говорят за себя, большинство из них дублируют списочные функции, так что я просто перечислю некоторые из их и дам эту ссылку
(Перевести этот термин я не берусь)
List comprehensions позволяет конструировать списки в соответствии с математической нотацией:
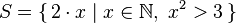
y может зависеть от x:
List comprehensions тоже синтаксический сахар и разворачивается в (последний пример):
В следующий раз я попробую ответить на все вопросы, а потом можно будет приниматься за реализацию чата (или сразу, если вопросов будет мало/не будет), так что спрашивайте, если что непонятно по всем статьям.
Классы привносят динамический полиморфизм, как и интерфейсы в традиционных императивных языках, а также могут быть использованы как замены отсутствующей в Хаскеле перегрузки функций.
Я расскажу, как определить класс типов, его экземпляры (instance) и как это всё устроено внутри.
Предыдущие статьи:
Типы данных, паттернг матчинг и функции
Основы
Классы типов
Предположим, вы написали свой тип данных и хотите написать для него оператор сравнения. Проблема в том, что перегрузки функций в Хаскеле нет и потому использовать для этих целей (==) простым способом не получится. Более того, придумывать для каждого типа новое имя — не вариант.
Но вы можете определить класс типов «сравниваемый». Тогда, если ваш тип данных принадлежит к этому классу, значения этого типа можно будет сравнивать.
class MyEq a where
myEqual :: a -> a -> Bool
myNotEqual :: a -> a -> BoolMyEq — это имя класса типов (как и типы данных, оно должно начинаться с заглавной буквы), a — некий принадлежащий к данному классу тип. Параметров у класса может быть несколько (FooClass a b c), но в данном случае только один.Тип
a принадлежит к классу MyEq, если для него определены соотстветствующие функции.В классе можно дать определение функции по умолчанию. Например, функции
myEqual и myNotEqual могут быть выражены друг через друга: myEqual x y = not (myNotEqual x y)
myNotEqual x y = not (myEqual x y)Теперь напишем экземпляр класса для
Bool:instance MyEq Bool where
myEqual True True = True
myEqual False False = True
myEqual _ _ = Falseinstance, затем вместо переменной типа a в определении самого класса мы пишем тот тип, для которого определяется экзмепляр, т.е. Bool.Определяем одну функцию
myEqual и теперь можно проверить в интерпретаторе результат:ghci> myEqual True True
True
ghci> myNotEqual True False
True
ghci> :t myEqual
myEqual :: (MyEq a) => a -> a -> BoolmyEqual накладывает ограничение (constraints) на тип — он должен принадлежать к классу MyEq.Такие же ограничения можно накладывать и при объявлении самого класса:
class (MyEq a) => SomeClass a where
-- ...Классы чем-то похожи на интерфейсы — мы объявляем фукнции, для которых потом предоставляем реализации. Другие функции могут использовать эти функции только если для некоторого типа есть такая реализация.
Однако есть существенные отличия как в возможностях, так и в реализации самого механизма.
- Как видно по функции
myEqual, она принимает два значения типаa, тогда как виртуальная функция принимает только один скрытый параметрthis.
Даже если у нас естьinstance MyEq Boolиinstance MyEq Int, вызов функцииmyEqual True 5приведёт к неудаче:
Компилятор (интерпретатор) знает, что параметрыghci> myEqual True (5::Int)
<interactive>:1:14:
Couldn't match expected type `Bool' against inferred type `Int'
In the second argument of `myEqual', namely `(5::Int)'
In the expression: myEqual True (5 :: Int)
In the definition of `it': it = myEqual True (5 :: Int)
ghci>myEqualдолжны иметь один тип и потому предотвращает такие попытки. - Экземпляр класса может быть определён в любой момент, что также очень удобно. Наследование от интерфейсов же указывается при определении самого класса.
- Функция может потребовать принадлежность типа данных сразу к нескольким классам:
Как это сделать, например, в С++/C#? Создавать композитныйfoo :: (Eq a, Show a, Read a) => a -> String -> StringIEquableShowableReadable? Но от него не отнаследуешься. Передавать аргумент три раза с приведением к разным интерфейсам и полагать внутри функции, что это один и тот же объект, а ответственность лежит на вызывающей стороне?
Раз уж упомянул C++, то заодно скажу, что в новом стандарте C++0x concept и concept_map есть суть классы типов, но используемые на этапе компиляции :)
Но есть и недостаток. Как нам завести список объектов, которые, к примеру, принадлежат к классу
Show (функция show :: a -> String)?Способ есть, но он нестандартен. В начало файла необходимо добавить соответствующие опции GHC:
{-#
OPTIONS_GHC
-XExistentialQuantification
#-}
-- Не знаю, почему, но при выравнивании TAB'ом GHC опции игнорировалdata ShowObj = forall a. Show a => ShowObj aИ заодно определить для него экземляр класса
Show, чтобы он сам также к нему принадлежал:instance Show ShowObj where
show (ShowObj x) = show xghci> [ShowObj 4, ShowObj True, ShowObj (ShowObj 'x')]
[4,True,'x']show я явно не вызывал, интерпретатор использует именно её, так что можно быть уверенным, что всё работает.Как это всё реализуется?
В функцию, которая накладывает ограничения на тип, передаётся скрытый параметр (на каждый класс и тип — свой) — словарь со всеми необходимыми функциями.
Фактически,
instance — это определение экземпляра словаря для конкретного типа.Чтобы было проще это понять, я просто приведу псевдо-реализацию для класса
Eq на Haskell'е и на C++:-- class MyEq
data MyEq a = MyEq {
myEqual :: a -> a -> Bool,
myNotEqual :: a -> a -> Bool}
-- instance MyEq Bool
myEqBool = MyEq {
myEqual = \x y -> x == y,
myNotEqual = \x y -> not (x == y)}
-- foo :: (MyEq a) => a -> a -> Bool
foo :: MyEq a -> a -> a -> Bool
foo dict x y = (myEqual dict) x y
-- foo True False
fooResult = foo myEqBool True False#include <iostream><br/>
<br/>
// class MyEq a<br/>
class MyEq<br/>
{<br/>
public:<br/>
virtual ~MyEq() throw() {}<br/>
// принимаем void const *, так как сам тип в базовом классе неизвестен<br/>
virtual bool unsafeMyEqual(void const * x, void const * y) const = 0;<br/>
virtual bool unsafeMyNotEqual(void const * x, void const * y) const = 0;<br/>
};<br/>
<br/>
// Шаблонная обёртка, знающая о типе и потому определяющая<br/>
// безопасные виртуальные функции<br/>
template <typename T><br/>
class MyEqDictBase : public MyEq<br/>
{<br/>
virtual bool unsafeMyEqual(void const * x, void const * y) const<br/>
{ return myEqual(*static_cast<T const *>(x), *static_cast<T const *>(y)); }<br/>
virtual bool unsafeMyNotEqual(void const * x, void const * y) const<br/>
{ return myNotEqual(*static_cast<T const *>(x), *static_cast<T const *>(y)); }<br/>
public:<br/>
virtual bool myEqual (T const & x, T const & y) const { return !myNotEqual(x, y); }<br/>
virtual bool myNotEqual (T const & x, T const & y) const { return !myEqual(x, y); }<br/>
};<br/>
<br/>
// Экземпляры классов. Определяться будут через специализацию.<br/>
template <typename T><br/>
class MyEqDict;<br/>
<br/>
// Создать словарь для определённого экземпляра класса<br/>
template <typename T><br/>
MyEqDict<T> makeMyEqDict() { return MyEqDict<T>(); }<br/>
<br/>
// instance MyEq Bool<br/>
// Экземпляр класса MyEq для bool<br/>
template <><br/>
class MyEqDict<bool> : public MyEqDictBase<bool><br/>
{<br/>
public:<br/>
virtual bool myEqual(bool const & l, bool const & r) const { return l == r; }<br/>
};<br/>
<br/>
// Функиця принимает словарь и два параметра<br/>
// То, что эти параметры на самом деле bool, гарантируется компиляторов Haskell'я<br/>
bool fooDict(MyEq const & dict, void const * x, void const * y)<br/>
{<br/>
return dict.unsafeMyNotEqual(x, y); // myNotEqual<br/>
}<br/>
<br/>
// Вспомогательная функция<br/>
// foo :: (MyEq a) => a -> a -> Bool<br/>
template <typename T><br/>
bool foo (T const & x, T const & y)<br/>
{<br/>
return fooDict(makeMyEqDict<T>(), &x, &y);<br/>
}<br/>
<br/>
int main()<br/>
{<br/>
std::cout << foo(true, false) << std::endl; // 1<br/>
std::cout << foo(false, false) << std::endl; // 0<br/>
return 0;<br/>
}Некоторые стандартные классы и синтаксический сахар
Enum — перечисление. Определяет функции для получение следующего/предыдущего значения, а также значения по номеру.
Используется в синтаксическом сахаре для списков
[1 .. 10], фактически, это означает enumFromTo 1 10, [1,3 .. 10] => enumFromThenTo 1 3 10Show — преобразование в строку, основная функция
show :: a -> String.Используется, например, интерпретатором для вывода значений.
Read — преобразование из строки, основная функция
read :: String -> a.Не знаю, почему выбрали возвращение значения, а не
Maybe a (опциональное значение), чтобы сигнализировать об ошибке «чистым» способом, а не «грязным» исключением.Eq — сравнение, операторы
(==) и (/=) (как бы перечёркнутый знак равенства)Ord — упорядоченные типы, операторы
(<) (>) (<=) (>=). Требует принадлежности типа к классу Eq.Более полный список различных классов можно посмотреть здесь.
Functor — функтор, функция
fmap :: (a -> b) -> f a -> f b.Чтобы было понятно, приведу примеры применения этой функции:
ghci> fmap (+1) [1,2,3]
[2,3,4]
ghci> fmap (+1) (Just 6)
Just 7
ghci> fmap (+1) Nothing
Nothing
ghci> fmap reverse getLine
hello
"olleh"map, для опционального значения Maybe a функция (+1) применяется, если само значение есть, а для ввода-вывода функция применяется к результату этого ввода-вывода.Подробнее про ввод-вывод я напишу далее, сейчас можно просто запомнить, что
getLine не возвращает строку, так что применить к нему reverse напрямую не получится.Чтобы каждый раз не определять экземпляры для вновь написанных типов данных, Haskell умеет делать это автоматически для некоторых классов.
data Test a = NoValue | Test a a deriving (Show, Read, Eq, Ord)
data Color = Red | Green | Yellow | Blue | Black | Write deriving (Show, Read, Enum, Eq, Ord)ghci> NoValue == (Test 4 5)
False
ghci> read "Test 5 6" :: Test Int
Test 5 6
ghci> (Test 1 100) < (Test 2 0)
True
ghci> (Test 2 100) < (Test 2 0)
False
ghci> [Red .. Black]
[Red,Green,Yellow,Blue,Black]Великие и ужасные монады
Класс Monad представляет собой «вычисление», т.е. он позволяет описывать способ комбинирования вычислений и результатов.
Вряд ли я напишу статью лучше, чем есть уже написанные, так что я просто дам ссылки на лучшие (по моему мнению) статьи для понимания, для чего эти монады нужны.
1. Монады — статья с SPbHUG о монадах на русском языке и с аналогиями на привычных императивных языках.
2. IO inside — статья на английском о вводе-выводе с использованием монад
3. Yet Another Haskell Tutorial — книга по Хаскелю, в разделе Monads очень хорошо написано на примере создания класса Computation, который суть и есть монада.
Здесь я напишу очень вкратце, чтобы можно было потом подглядеть.
Допутим, мы хотим описать последовательные вычисления, где каждое следующее зависит от результатов предыдущего (некоторым не заданным наперёд способом). Для этого можно определить соответствующий класс, в котором должны быть как минимум две функции:
class Computation c where
return :: a -> c a
bind :: c a -> (a -> c b) -> c bВторая функция принимает 2 аргумента:
1. вычисление, которое при выполнении вернёт значение типа
a2. функцию, которое примет значение типа
a и вернёт новое вычисление, возвращающее значение типа bРезультатом будет вычисление, которое вернёт значение типа
b.Зачем всё это может быть нужно, я покажу на примере опционального значения
data Maybe a = Just a | NothingNothing. Тогда, используя их напрямую, мы рискуем получить такой слабочитаемый код:funOnMaybes x =
case functionMayFail1 x of
Nothing -> Nothing -- первая функция ничего нам не вернула, и мы тоже ничего не вернём
Just x1 -> -- отлично, первая функция вернула некоторое значение, продолжим с ним работу
case functionMayFail2 x1 of
Nothing -> Nothing -- теперь вторая функция ничего не вернула (точнее вернула "ничего")
Just x2 -> -- и так далееНо ведь у нас язык позволяет передавать функции в качестве аргументов и возвращать так же, воспользуемся:
combineMaybe :: Maybe a -> (a -> Maybe b) -> Maybe b
combineMaybe Nothing _ = Nothing
combineMaybe (Just x) f = f xcombineMaybe принимает опциональное значение и функцию, а возвращает результат применения этой функции к опциональному значению, либо неудачу.Перепишем функцию
funOnMaybes:funOnMaybes x = combineMaybe (combineMaybe x functionMayFail1) functionMayFail2 --...funOnMaybes x = x `combineMaybe` functionMayFail1 `combineMaybe` functionMayFail2 --...Можно заметит, что тип функции
combineMaybe в точности повторяет тип bind, только вместо c стоит Maybe.instance Computation Maybe where
return x = Just x
bind Nothing f = Nothing
bind (Just x) f = f xMaybe, только bind там называется (>>=), плюс есть дополнительный оператор (>>), который не использует результат предыдущего вычисления.Кроме того, для монад определён синтаксический сахар, который значительно упрощает их использование:
funOnMaybes x = do
x1 <- functionMayFail1 x
x2 <- functionMayFail2 x1
if x2 == (0)
then return (0)
else do
x3 <- functionMayFail3 x2
return (x1 + x3)do внутри else и на его отсутствие в then. do — это всего лишь синтаксический сахар, который комбинирует несколько вычислений в одно, а так как в ветке then вычисление и так одно (return (0)), то do там не нужен; в ветке else вычисления два подряд, и чтобы их скомбинировать, надо снова использовать do.Специальный синтаксис с обратной стрелкой
(<-) преобразуется очень просто:1. do {e} -> e
do с одним вычислением есть само это вычисление, комбинировать ничего не нужно
2. do {e; es} -> e >> do {es}
несколько подряд идущих вычислений соединяются оператором
(>>)3. do {let decls; es} -> let decls in do {es}
внутри do можно заводить дополнительные декларации наподобие
let ... in4. do {p < — e; es} -> let ok p = do {es}; ok _ = fail "..." in e >>= ok
если результат первого вычисления используется в дальнейшем, то для комбинации используется оператор
(>>=)В последнем случае такая конструкция используется потому, что в качестве
p может выступать образец, который может и не совпасть.Если он совпадёт, то будет выполнено дальшейшее вычисление, в противном случае будет возвращена ошибка со строковым описанием.
Функция
fail — ещё одна дополнительная функция в монаде, которая вообще говоря к концепции монад отношения не имеет.Какие ещё экземпляры монад есть в стандартной библиотеке?
State — вычисления с состоянием. При помощи функций
get/put, которые знают о внутреннем устройстве State, можно получать и устанавливать состояние.import Control.Monad.State
fact' :: Int -> State Int Int -- тип состояния - Int, тип результата - тоже Int
fact' 0 = do
acc <- get -- получаем накопленный результат
return acc -- возвращаем его
fact' n = do
acc <- get -- получаем аккумулятор
put (acc * n) -- домножаем его на n и сохраняем
fact' (n - 1) -- продолжаем вычисление факториала
fact :: Int -> Int
fact n = fst $ runState (fact' n) 1 -- начальное значение состояния - 1runState вычисляет функцию с состоянием, возвращает кортеж с результатом и изменённым состоянием. Нам нужен только результат, поэтому fst.Список — тоже монада. Последующие вычисления применяются ко всем результатам предыдущего.
dummyFun contents = do
l <- lines contents -- получаем все строки
if length l < 3 then fail "" -- строки менее 3 символов игнорируем
else do
w <- words l -- разбиваем строку на слова
return w -- возвращаем словоghci> dummyFun "line1\nword1 word2 word3\n \n \nline5"
["line1","word1","word2","word3","line5"]Continuations (продолжения) в Хаскеле — тоже монада — Cont
Про продолжения можно почитать на русской вики и английской вики и далее по ссылкам.
Они заслуживают отдельного внимания, но всё я не умещу, да и к монадам они непосредственного отношения не имеют.
Хорошая статья про продолжения в Scheme есть у пользователя palm_mute в живом журнале.
Ввод-вывод тоже реализован с использованием монады. Например, тип функции
getLine:getLine :: IO StringIO можно понимать так:getLine :: World -> (String, World)World — состояние мират.е. любая функция ввода-вывода как бы принимает состояние мира, а возвращает некоторый результат и новое состояние мира, которое затем используется последующими функциями.
Разумеется, это всего лишь мысленное представление.
Так как в отличие от списков и Maybe у нас нет конструкторов типа
IO, то мы никогда не сможем результат типа IO String разобрать на составляющие, а обязаны будем только использовать его в других вычислениях, таким образом гарантируется, что использование ввода-вывода будет отражено в типе функции.(«Никогда» — это громко сказано, на самом деле есть
unsafePerformIO :: IO a -> a, но на то и unsafe, чтобы использоваться только с пониманием дела и когда это крайне необходимо. Я лично ни разу не использовал).Стоит упомянуть Monad transformers (трансформаторы монад).
Если нам нужно состояние, мы можем использовать
State, если ввод-вывод — IO. А что если наша функция хочет иметь состояния и при этом осуществлять ввод-вывод?Для этого предназначен трансформер StateT, который соединяет
State и другую монаду. Для выполнения вычислений в этой другой монаде используется функция lift.Посмотрим на примере факториала, который мы изменим так, чтобы он печатал аккумулятор
import Control.Monad.State
fact' :: Int -> StateT Int IO Int -- добавили IO
fact' 0 = do
acc <- get
return acc
fact' n = do
acc <- get
lift $ print acc -- print acc - вычисление типа IO (), поэтому его мы передаём функции lift
put (acc * n)
fact' (n - 1)
fact :: Int -> IO Int -- Пришлось поставить IO и здесь, никуда не деться :)
fact n = do
(r, _) <- runStateT (fact' n) 1
return rghci> fact 5
1
5
20
60
120
120Кроме StateT есть также ListT (для списка).
Полный список монад и трансформеров монад.
Для удобства над монадами определены обобщённые функции. Их названия говорят за себя, большинство из них дублируют списочные функции, так что я просто перечислю некоторые из их и дам эту ссылку
sequence :: Monad m => [m a] -> m [a]
-- выполнить последовательно все вычисления и вернуть список результатов
mapM f = sequence.map f
forM = flip mapM
-- forM [1..10] $ \i -> print i
forever :: Monad m => m a -> m b -- думаю, пояснять не надо
filterM :: Monad m => (a -> m Bool) -> [a] -> m [a] -- filter
foldM :: Monad m => (a -> b -> m a) -> a -> [b] -> m a -- foldl
when :: Monad m => Bool -> m () -> m () -- if без ветки elseList comprehensions
(Перевести этот термин я не берусь)
List comprehensions позволяет конструировать списки в соответствии с математической нотацией:
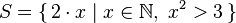
ghci> take 5 $ [2*x | x <- [1..], x^2 > 3]
[4, 6, 8, 10, 12]
ghci> [(x, y) | x <- [1..3], y <- [1..3]]
[(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)]y может зависеть от x:
ghci> [x + y | x <- [1..4], y <- [1..x], even x]
[3,4,5,6,7,8]List comprehensions тоже синтаксический сахар и разворачивается в (последний пример):
do
x <- [1..4]
y <- [1..x]
True <- return (even x)
return (x + y)В следующий раз я попробую ответить на все вопросы, а потом можно будет приниматься за реализацию чата (или сразу, если вопросов будет мало/не будет), так что спрашивайте, если что непонятно по всем статьям.