Так и подмывало озаглавить тему: «Закат компании Гугл близок!», но все-таки слишком уж «желто» было бы.
Теперь к делу. Что такое «гомоморфное шифрование» и причем тут Гугл?
Гомоморфным шифрованием называют такую криптосистему, которая позволяет совершать некоторые математические действия с открытым текстом путем произведения операций с зашифрованным (возможно другое математическое действие или даже ряд операций). Например, RSA гомоморфна для операции умножения (тривиально из самого шифрования).
Удивительно, но до недавних пор не существовало криптосистемы гомоморфной для операций умножения и суммирования одновременно, так называемого полностью гомоморфного шифрования (fully homomorphic encryption), т.к. суммы и умножения хватит, чтобы выразить любую математическую функцию. Главная проблема с предыдущими схемами была в том, что каждая операция добавляет некоторый «шум» в криптотекст (посмотрите на формулу RSA и вспомните определение mod), поэтому через некоторое количество шагов накопленный шум делает расшифровку невозможной. Насколько я помню из презентации, говорилось, что подобные схему все же существуют, но они экспоненциональны по «эффективности».
Крэйг Гэнтри (Craig Gentry, PhD Stanford, IBM Research) опубликовал пример первой такой функции в своей PhD диссертации. Не вдаваясь в подробности (да и не буду делать вид, что на 100% понял все математические выкладки), смысл его решения заключается в том, что он использует двойное шифрование. Т.е. через определенное количество шагов он «снимает верхний слой» (первое шифрование) и «убирает» накопившийся «шум».
Как это работает, я расскажу общими словами и примерами, которые он сам использовал в своей презентации. Кому интересна математика и более формальное объяснение — читать диссертацию.
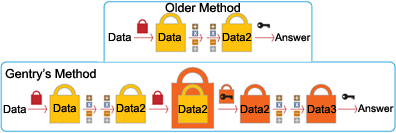
Пример, который он приводил довольно прост. Представьте, что ювелир работает с драгоценностями. Чтобы исключить воровство, эти драгоценности ему даются в прозрачном ящике с перчатками, чтобы он мог работать. Кроме того, к сожалению данные перчатки портятся после определенного промежутка времени (вспомним, про накопление «шума»), поэтому каждый раз когда перчатки вот-вот должны испортиться, этот первоначальный ящик вставляют внутрь идентичного ящика. И так продолжается до тех пор, пока работа не завершена.
Конечно, данный пример не идеален, но он дает некоторое представление о работе полной гомоморфной функции Гэнтри.
Теперь вспомним причем же тут Гугл? А смысл в том, что если этот алгоритм внедрить, например, в Гугл, то они не смогут узнать ваш запрос и даже ответ. Зачем им это делать, это, конечно, уже другой вопрос. Более интересный пример, это налоговые декларации. Представьте, что вы отсылаете зашифрованную вашим закрытым ключом декларацию и получаете также зашифрованный результат от налогового специалиста, который не узнал ни бита информации о ваших доходах.
К сожалению, хоть и текущая реализация полной гомоморфной системы работает за полиномиальное время, константы там «неприлично огромные», поэтому в ближайшее будущее Гугл может спать спокойно.
UPDХотелось бы упомянуть интересный факт из биографии Крэйга. Он получил бакалавра математики в университете Дьюка, потом закончил юридическую школу Гарварда, а потом решил, что для полного счастья ему не хватает PhD в computer science! Решение проблемы, описанной в статье, он нашел будучи на стажировке в IBM Research.
Теперь к делу. Что такое «гомоморфное шифрование» и причем тут Гугл?
Гомоморфным шифрованием называют такую криптосистему, которая позволяет совершать некоторые математические действия с открытым текстом путем произведения операций с зашифрованным (возможно другое математическое действие или даже ряд операций). Например, RSA гомоморфна для операции умножения (тривиально из самого шифрования).
Удивительно, но до недавних пор не существовало криптосистемы гомоморфной для операций умножения и суммирования одновременно, так называемого полностью гомоморфного шифрования (fully homomorphic encryption), т.к. суммы и умножения хватит, чтобы выразить любую математическую функцию. Главная проблема с предыдущими схемами была в том, что каждая операция добавляет некоторый «шум» в криптотекст (
Крэйг Гэнтри (Craig Gentry, PhD Stanford, IBM Research) опубликовал пример первой такой функции в своей PhD диссертации. Не вдаваясь в подробности (да и не буду делать вид, что на 100% понял все математические выкладки), смысл его решения заключается в том, что он использует двойное шифрование. Т.е. через определенное количество шагов он «снимает верхний слой» (первое шифрование) и «убирает» накопившийся «шум».
Как это работает, я расскажу общими словами и примерами, которые он сам использовал в своей презентации. Кому интересна математика и более формальное объяснение — читать диссертацию.

Пример, который он приводил довольно прост. Представьте, что ювелир работает с драгоценностями. Чтобы исключить воровство, эти драгоценности ему даются в прозрачном ящике с перчатками, чтобы он мог работать. Кроме того, к сожалению данные перчатки портятся после определенного промежутка времени (вспомним, про накопление «шума»), поэтому каждый раз когда перчатки вот-вот должны испортиться, этот первоначальный ящик вставляют внутрь идентичного ящика. И так продолжается до тех пор, пока работа не завершена.
Конечно, данный пример не идеален, но он дает некоторое представление о работе полной гомоморфной функции Гэнтри.
Теперь вспомним причем же тут Гугл? А смысл в том, что если этот алгоритм внедрить, например, в Гугл, то они не смогут узнать ваш запрос и даже ответ. Зачем им это делать, это, конечно, уже другой вопрос. Более интересный пример, это налоговые декларации. Представьте, что вы отсылаете зашифрованную вашим закрытым ключом декларацию и получаете также зашифрованный результат от налогового специалиста, который не узнал ни бита информации о ваших доходах.
К сожалению, хоть и текущая реализация полной гомоморфной системы работает за полиномиальное время, константы там «неприлично огромные», поэтому в ближайшее будущее Гугл может спать спокойно.
UPDХотелось бы упомянуть интересный факт из биографии Крэйга. Он получил бакалавра математики в университете Дьюка, потом закончил юридическую школу Гарварда, а потом решил, что для полного счастья ему не хватает PhD в computer science! Решение проблемы, описанной в статье, он нашел будучи на стажировке в IBM Research.