
Сегодня мы снова поговорим про протокол Диффи-Хеллмана, но уже построенный на более необычных конструкциях — изогениях, которые признаны устойчивыми к атакам на будущем квантовом компьютере. Квантовый компьютер, который сможет удержать в связанном состоянии порядка нескольких тысяч кубит, позволит находить закрытые ключи по открытым ключам у всех используемых сейчас асимметричных криптосистем. Число кубит для взлома RSA равно удвоенному числу бит в модуле (т.е. для разложения на множители модуля RSA длиной 2048 бит потребуется 4096 кубит). Для взлома эллиптических кривых необходимы более скромные мощности «квантового железа»: для решения задачи ECDLP для кривых над простым полем (такие кривые есть и в отечественном стандарте подписи ГОСТ Р 34.10-2012 и в американском ECDSS) c модулем кривой длиной n бит требуется 6n кубит (т. е. для модуля в 256 бит надо ~ 1536 кубит, а для 512 бит ~ 3072 кубит). На днях российско-американская группа ученых установила мировой рекорд, удержав в связанном состоянии 51 кубит. Так что у нас есть еще немного времени для изучения изогений (а также решеток, кодов, multivariate и подписей, основанных на хэшах).
Кстати, изогении считаются одним из наиболее вероятных кандидатов на победу на конкурсе NIST постквантовых алгоритмов для замены RSA и эллиптических кривых в ближайшие несколько лет. Предыдущую статью про прошлое и настоящее Диффи-Хеллмана можно почитать тут .
Что такое изогении?
Отображение, которое переводит точки одной кривой E1 в точки другой кривой E2 (либо в саму себя (тогда считаем E2 = E1)) следующим образом: если на кривой E1 мы выберем любые две точки A1 и B1 и отобразим их в точки A2 и B2 на кривой E2, тогда то же самое отображение обязательно переведет их сумму — точку С1 = A1 + B1 именно в точку С2 = A2 + B2 – сумму их отображений. Это замечательное свойство называется сохранением операции, а такое отображение является гомоморфизмом. Изогению можно выразить с помощью рациональной функции: точка (x, y) отображается в точку с координатами
Если существует такого рода отображение между двумя кривыми, то они называются изогенными. Частный случай изогении — это изогения кривой на саму себя (эндоморфизм).
Каким свойством должны обладать две кривые, чтобы быть изогенными?
Теорема Tate:
Две кривые над одним конечным полем изогенны тогда и только тогда, когда порядки их групп равны.
Пример 1 (изогения кривой на саму себя):
Эндоморфизм: скалярное умножение точки на число:
например, для n = 2 и
Для произвольного n аналогичная (но более длинная) формула может быть получена рекуррентно при помощи так называемых полиномов деления (division polynomials)
Пример 2 (изогения между разными кривыми):
Пусть есть кривая
и кривая
Порядки групп (т.е. число точек на кривой) у E1 и E2 равны: #E1 = #E1 = 21
По теореме Тейта равенство #E1 = #E1 означает, что между E1 и E2 существует изогения.
j–инвариант E1 = 6, а j–инвариант E2 = 4. Т.е группы точек кривых не изоморфны.
(изоморфизм — это частный случай гомоморфизма, когда каждому элементу в отображении соответствует только один элемент образа (т.е. несколько элементов не переходят в один: отображение только «один в один»))
Изогения, которая отображает точки с E1 на E2 (откуда она взялась мы покажем в Примере 3) может быть представлена с помощью следующего рационального отображения:
Отображение
Рассмотрим, к примеру, точки A1 (9, 6) и B1 (14, 2) кривой E1. Их сумма — точка С1 с координатами (5, 6). Если подставить их в формулу выше, то получим их отображение на кривую E2, Соответствующие им точки на E2 — A2, B2, C2:
A1 (9, 6) → A2 (14, 1)
B1 (14, 2) → B2 (17, 4)
C1 (5, 6) → C2 (8, 5)
Легко проверить, что С2 = A2 + B2. Т.е. точка С1 = A1 + B1 переходит в точку С2 = A2 +B2. Если не лень, то можно перебрать все комбинации из любых двух точек E1 A и B и их отображений φ(A) и φ(B) и убедиться, что они ведут себя аналогично:
А что будет, если подставить точки (2, 12) или (2, 7)? Знаменатель правой дроби будет равен нулю! Это всего лишь означает, что эти точки переходят в точку на бесконечности для E2.
Осталось рассмотреть точку на бесконечности на E1. Она «по умолчанию» переходит в точку на бесконечности на E2. Это фундаментальное свойство гомоморфизма: нейтральный элемент (в случае эллиптических кривых — это точка на бесконечности) отображается в нейтральный элемент. Иначе “сломается” сохранение операции для случая, когда один двух элементов – нейтральный.
Степенью изогении называется степень полинома
В Примере 2
Вычисление изогений
Как найти такие отображения? Оказывается, что число возможных изогений для конкретной кривой равно количеству подгрупп в группе ее точек. Существует детерминированный алгоритм который придумал математик Велю (Velu') в 1971 году. Он использует много формул, поэтому сначала покажем его общую схему:
Вход:
кривая
Выход:
кривая
Сложность алгоритма:
Обозначение:
На выходе мы получаем коэффициенты
А теперь объясним, зачем мы все это нагромоздили (и будем дальше это делать):
также, как для мультипликативных групп конечного поля и эллиптических кривых, для изогении существует своя сложная задача, которую можно (и нужно) использовать для создания ЭЦП и аналогов Диффи-Хеллмана.
Сложная задача для изогений:
Даны две изогенные кривые
Если мы имеем две кривые, про которые мы знаем, что они изогенные (а это так, если равны порядки их групп), но не знаем при помощи какой подгруппы можно получить эту изогению. Очевидно, что число подгрупп должно быть большим настолько, чтобы было вычислительно сложно найти изогению простым перебором, подставляя подгруппы в алгоритм Velu'.
Алгоритм Velu':
Вход:
кривая
1. Отбрасываем точку на бесконечности
2. Находим
3. Разбиваем
4. Множество
Для каждой точки
Коэффициенты
Итак, изогенную кривую мы знаем. Как вычислить отображение
Выход алгоритма Velu':
Коэффициенты
Пример 3 (Алгоритм Velu'. Как была получена изогения в Примере 2):
Вход :
1. Отбрасываем точку на бесконечности
2. Точек четного порядка нет в
3. Выбираем для
4. Множество
Цикл из одного шага: (т.к. в
Осталось только посчитать рациональное отображение:
Аналогично приводим формулу для β к общему знаменателю:
Выход:
Коэффициенты изогенной кривой:
Отображение
Вычисление изогений большой степени
Легко видеть, что в алгоритме Velu имеются подводные камни: он работает в цикле, пока не пройдется по всем точкам из множества
Обозначение: Кривую
Пусть
Разложим изогению
Пример 4
Мы хотим вычислить изогению для циклической группы порядка
Вместо того, чтобы один раз применить алгоритм Velu' для группы применим его 4 раза, каждый раз считая изогению степени
Итак, теперь мы умеем вычислять изогении для циклических групп очень большого порядка. К примеру, если есть группа порядка
Практика: изогении между суперсингулярными кривыми
Напомним, что у двух изоморфных кривых одинаковый j-инвариант и для кривой
Из за того, что найти преобразование между изоморфными кривыми особой сложности не представляет, задача изогений по сути является задачей про нахождение изогений между различными классами изоморфных кривых (а каждый из этих классов можно представить в виде соответствующего j-инварианта).
Какие кривые представляют интерес для изогений? Ведь мы знаем, что существуют запрещенные семейства кривых для эллиптических Диффи-Хеллмана и ЭЦП: суперсингулярные, аномальные и гладкого порядка и.т.д. — для всех относительно легко решается задача ECDLP. Такие неприятные классы должны существовать и для изогений. Только тут ситуация совершенно иная, ведь трудная задача не ECDLP. Очевидно, что надо использовать кривые гладкого порядка, чтобы было больше подгрупп. Кроме того, в 2010 году исследователи из университета Ватерлоо выяснили, что использование обычных кривых небезопасно с «квантовой» точки зрения: был получен результат, который утверждал, что для криптосистем, использующих изогении безопасно использовать только суперсингулярные кривые. Напомним, что это кривые, у которых след Фробениуса t такой что t mod p = 0, где p — характеристика поля кривой (сам след Фробениуса связан с порядком группы кривой #
Какое поле для кривой оптимальнее было бы использовать? Сразу напрашивается ответ — старое доброе простое поле
У таких кривых есть интересные свойства:
Граф изогений фиксированной степени — правильный. (т.е у каждой вершины имеется одинаковое число ребер)
Для любого простого числа
Пример 5 (пример и изображения графов — Dr. Fre Vercauteren)
Рассмотрим поле
Выберем неприводимый многочлен:
Множество j-инвариантов будет таким:
105, 64, 155w + 3, 74w + 50, 86w + 227, 167w + 31, 175w + 237, 66w + 39, 8, 23w + 193, 218w + 21, 28, 49w + 112, 192w + 18 }
Их число #
Для кривых порядка #
Для изогении степени
Каждая кривая имеет 3 изогении степени 2
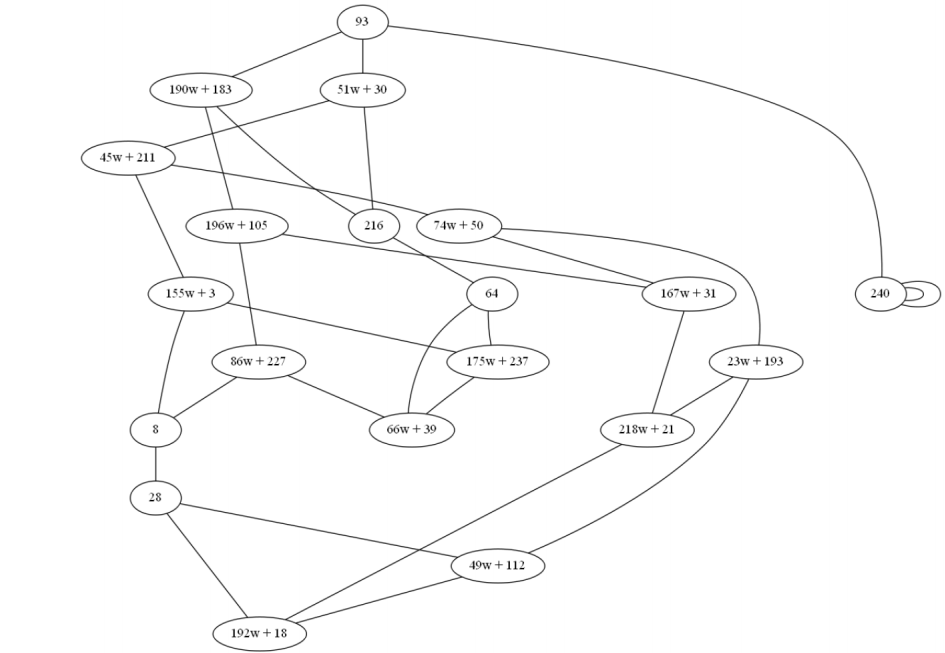
Для изогении степени
Каждая кривая имеет 4 изогении степени 3
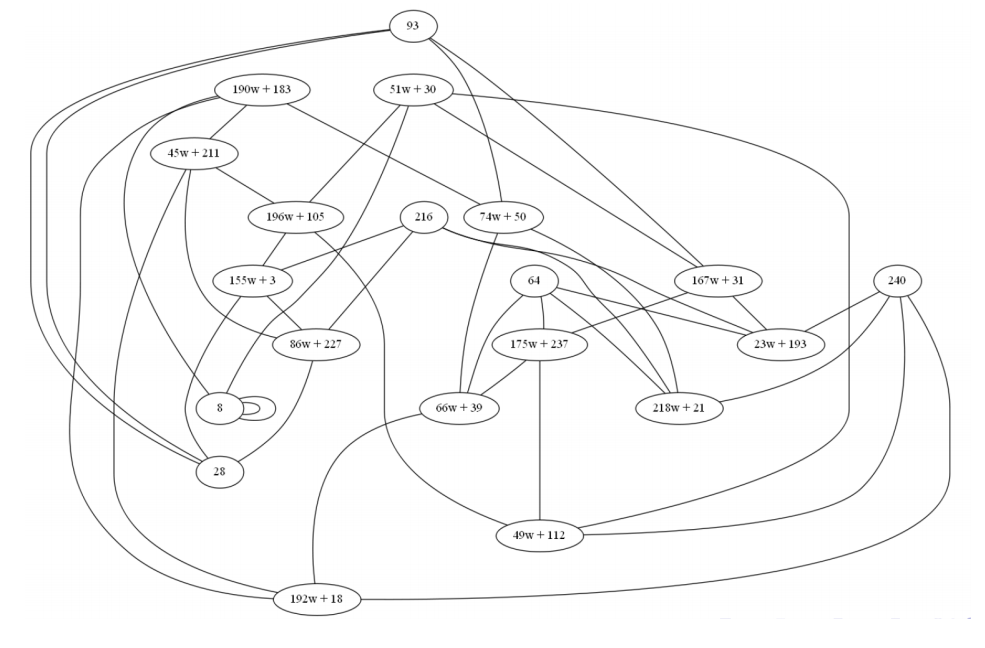
Аналогично для
Каждая кривая имеет 12 изогении степени 11.
Сложную задачу, которую придется решать злоумышленнику, теперь можно сформулировать так: зная две кривые
Supersingular Isogeny Diffie-Hellman (SIDH)
Определение:
Если при умножении точки
Подгруппа n-кручения (n-torsion subgroup)
Эта подгруппа состоит из точки на бесконечности и всех точек n-кручения.
Очевидно, что точкой n-кручения является точка, если ее порядок делит n без остатка.
Выбор поля
Пусть
При характеристике поля
Итак, пусть
характеристика поля
Подгруппы кручения
Выберем точки
Итак доменные параметры для SIDH (аналог доменных параметров для обычных эллиптических кривых):
кривая
(Примечание:
Тот, кто начинает (Алиса) использует для генерации пары базис
Алиса генерирует случайные
Затем она вычисляет вычисляет точку
И вычисляет с ее помощью изогению
после чего преобразует c помощью изогении
Закрытый ключ Алисы:
Открытый ключ Алисы: кривая
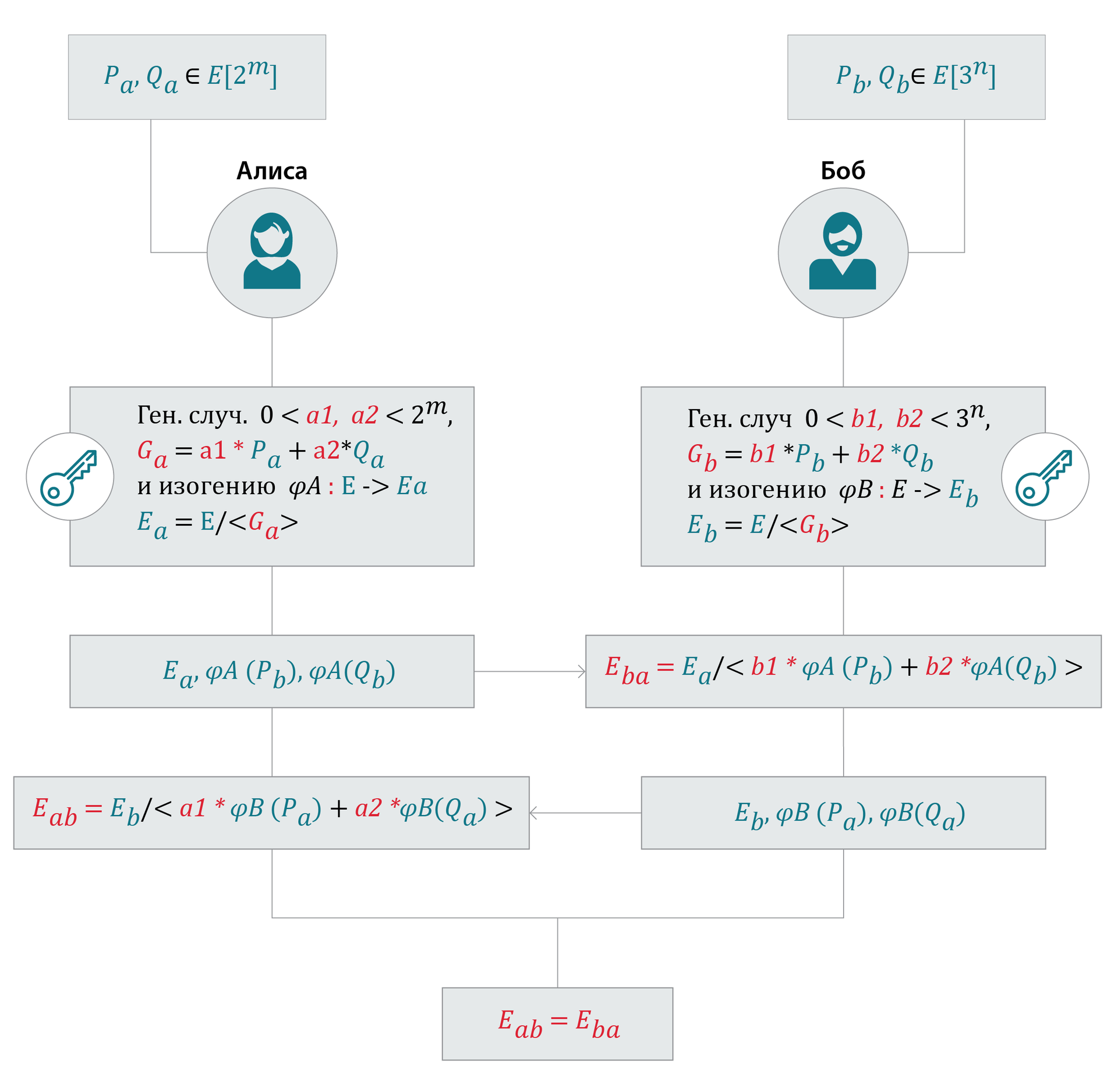
Аналогичные шаги делает Боб (см. диаграмму):
Закрытый ключ Боба:
Открытый ключ Боба: кривая
Алиса отправляет открытый ключ Бобу
Боб вычисляет точку
изогенную кривую
Далее, Боб отправляет Алисе открытый ключ и Алиса подобным образом вычисляет кривую
Для получения общего секрета Алиса вычисляет j-инвариант от
а Боб от
Безопасность и размеры ключей
Для успешной атаки надо найти путь хотя бы на одном из графов (Алисы или Боба). Эта задача имеет разные степени сложности для классического и квантовых компьютеров:
Классическая сложность: Алиса
Квантовая сложность: Алиса
Поэтому:
Классический уровень безопасности =
Квантовый уровень безопасности =
Размеры ключей:
Открытый ключ:
точки P и Q
коэффициенты A и B кривой
~ 8 *
~ 6 *
Длина характеристики поля = 768 бит:
768/6 = 128-битный квантовый уровень безопасности
768/4 = 192-битный классический уровень безопасности
Длина ключа 6
Длина характеристики поля = 1536 бит:
1536/6 = 256-битный квантовый уровень безопасности
1536/4 = 384-битный классический уровень безопасности
Длина ключа 6
Производительность
Лучшие результаты для 128-битного квантового уровня безопасности (характеристика поля
Для Intel Haswell на частоте 3,4 Ггц:
вычисляется за ~100 млн. тактов для одной из сторон (Алисы или Боба)
(используются кривые Монтгомери и проективные координаты)
Для чипа ARM7 Beagle Board Black Cortex-A8 на частоте 1 Ггц:
время выполнения — 1,5 сек. Если задействовать SIMD-инструкции NEON, то 0,2 сек.
Литература:
1. «Public-Key Cryptosystem Based on Isogenies», Alexander Rostovtsev, Anton Stolbunov, 2006
2. «Constructing elliptic curve isogenies in quantum subexponential time» Andrew M. Childs, David Jao, Vladimir Soukharev, 2010
3. «Towards Quantum-Resistant Cryptosystems from Supersingular Elliptic Curve Isogenies» David Jao, Luca De Feo, 2011
4. «Efficient algorithms for supersingular isogeny Diffie-Hellman» Craig Costello and Patrick Longa and Michael Naehrig, 2016
5. «NEON-SIDH: Efficient implementation of supersingular isogeny Diffie-Hellman Key Exchange protocol on ARM» R. Azarderaksh, D. Jao, 2016
6. «Mathematics of Public Key Cryptography» Steven D. Galbraith, Cambridge University Press