На примере парадокса Монти Холла посмотрим, что общего между статистикой и интуицией, и как визуализация данных может помочь принять правильное решение, основанное на статистической оценке.
Сложность парадокса Монти Холла
Парадокс Монти Холла получил свое название от ведущего телевизионного шоу "Let's Make a Deal". Игровая ситуация:
Перед игроком три двери, за одной из которых приз. Игрок выбирает одну из них, не открывая. После этого ведущий, открывает одну из двух оставшихся дверей. Ведущий знает, за какой из дверей приз, и всегда открывает дверь, за которой приза нет. Далее игроку предлагается поменять первоначально выбранную дверь на другую, остающуюся закрытой. Вопрос: повышаются ли шансы игрока при изменении выбранной двери?
Парадокс заключается в том, что интуитивно кажется, что смена двери ничего не дает. Приз либо за одной дверью, либо за другой. Ситуация симметричная, и вероятности одинаковы. Однако, теория вероятностей показывает, что смена двери повышает шансы выигрыша в два раза.
Чтобы прийти к статистически правильному решению, игрок должен:
- Мысленно перейти от выбора одной из двух дверей к выбору одной из двух стратегий: "stay" (оставить изначально выбранную дверь) и "switch" (сменить дверь на другую).
- Построить статистическую модель игровой ситуации и оценить обе стратегии.
- На основании статистических оценок отказаться от первоначально выбранной двери.
Первый шаг ключевой. Если остаться на уровне выбора дверей, то ничего не получится, ведь приз, так или иначе, за одной из двух дверей. А они выглядят одинаково — ситуация как будто симметричная. Можно не менять дверь и выиграть, можно поменять дверь и проиграть. Возможно, смена двери повышает шансы на успех, но не гарантирует его. Делая первый шаг, игрок не должен путать "повышение шансов" и "гарантированный выигрыш".
Второй шаг еще сложнее: построить и применить статистическую модель задачи. Цепочка рассуждений может быть такой.
Сначала игрок делает выбор одной из трех дверей. По условию приз размещен за любой из них с одинаковой вероятностью. На первом шаге вероятность выбора приза равна 1/3. На рисунке ниже изображено дерево решений после первоначального выбора игрока. Дверь, за которой приз, закрашена:

Дальше ведущий открывает одну из дверей, не выбранных игроком. Игроку кажется, что ведущий выбирает дверь, которую открыть. Однако, это не всегда так. Поведение ведущего обусловлено первым выбором игрока:
- Если игрок сразу выбрал дверь с призом, то ведущий может выбрать любую из двух закрытых. Ни за одной из них приза нет.
- Если игрок выбрал дверь без приза, то ведущий всегда открывает одну дверь. Дверь, за которой приз, ведущий открыть не может по условиям игры.
Вероятность того, что приз за дверью, которую ведущий оставил закрытой, рассчитывается по формуле условной вероятности. И эти вероятности различаются для разных исходов, как показывает дерево решений. Закрытые двери, за которыми приз, закрашены:

Игрок суммирует вероятности по каждой стратегии и получает их статистическую оценку. На рисунке видно, что вероятность выигрыша при смене двери (стратегия "switch") в два раза выше:

После того, как стратегии оценены, игрок должен отказаться от первоначального выбора. Это сложно само по себе. Игрок будет стремится сохранить первоначальный выбор, так как это проще. Например, потенциальный покупатель гораздо вероятнее не будет отключать по умолчанию включенную услугу, нежели включит ее. В общем случае это приводит к систематическому отклонению поведения игроков от рационального.
Трудности применения статистического мышления
Проблемы, связанные с применением статистического мышления и рационального мышления вообще рассматриваются в книге Дэвида Канемана "Думай медленно, решай быстро". Исследования Канемана и его коллег показали, что человек склонен ошибаться в ситуациях, если нужно провести даже простые математические расчеты, не говоря уже об оценке вероятности.
Канеман вводит понятие двух систем. Система 1 это "быстрое", интуитивное, эвристическое мышление. Им человек пользуется, например, для определения настроения по выражению лица или при оценке дорожной ситуации, когда ведет автомобиль. Система 1 это автоматическая, почти мгновенная реакция, и работает в большинстве повседневных ситуаций.
Система 2 — "медленное", рациональное, математическое и статистическое мышление. Эта система подключается с усилием. Человек должен осознать, что автоматическое решение неправильное, задуматься и провести расчеты.
Ключевая проблема заключается в том, что в ситуации, где требуется подумать, человек полагается на автоматическое решение, предлагаемое системой 1. А эта система делает выводы, в первую очередь, на основании похожести вариантов. В парадоксе Монти Холла, после того, как ведущий открыл одну из дверей, две оставшихся выглядят одинаково, а обусловленное поведение ведущего старательно замаскировано. Ситуация представляется симметричной, а вероятности одинаковыми. Системе 1 не за что зацепиться, чтобы заметить вероятностную асимметрию. А системе 2 некогда подключиться. Тем более, что ведущий разными способами старается сбить игрока с толку.
Система 1 тренируется на многократном повторении ситуаций, доводя выбор до автоматизма (распознавание лиц, вождение автомобиля). Человек видит похожую ситуацию, что-то, что ему знакомо, и делает выбор, который ранее был успешен в аналогичных ситуациях.
Система 2 подразумевает, что человек начинает анализировать ситуацию, чтобы принять решение. В случае со статистическими задачами правильный ответ не очевиден. Чтобы к нему прийти, человек должен проанализировать данные, произвести расчеты и выбрать наибольшие значения статистических показателей.
Общее между интуицией и статистикой
Основная идея Дэвида Канемана в том, что система 1 (интуитивная) и система 2 (рациональная) различаются. В общем случае так и есть, однако, применительно к статистике между ними есть сходство.
Предположим, что все участники шоу Монти Холла собрались, чтобы обсудить результаты участия в шоу. Собравшиеся разбились на две группы: тех, кто остался с первоначально выбранной дверью и тех, кто поменял дверь. Согласно статистике, подсчет участников и их результатов покажет, что те участники, которые меняли дверь, выигрывали чаще. Если участников в обеих группах много, то доля победителей в группе сменивших дверь, будет примерно в два раза выше, чем в другой.
Достаточное количество участников, при котором будет видна статистическая закономерность, определяется законом больших чисел. Чем больше игроков примет участие в собрании, тем более результаты подсчетов их успехов и неудач будут соответствовать теоретическим. Другими словами, статистика начинает работать, когда игра была повторена разными участниками много раз. Если бы такое сообщество игроков существовало, то со временем они бы пришли к правильной стратегии.
Таким образом, в статистических расчетах система 2 опирается на закон больших чисел — достаточно большое (в идеале бесконечное) количество испытаний. Но и системе 1 большое количество испытаний позволяет принимать правильные решения. Многократное повторение доводит ту или иную способность человека до автоматизма.
Правила для двух систем:
- Система 1: это было правильно для меня много раз в похожих случаях, поэтому будет верно и сейчас.
- Система 2: это было правильно для многих других людей в похожих случаях, поэтому будет верно и сейчас.
Можно сказать, что расчет вероятности отражает коллективный опыт всех реальных и возможных участников игры Монти Холла. Для ситуаций индивидуального выбора стратегий статистика выступает как коллективная интуиция. Остается сделать статистику наглядной при помощи подходящей визуализации.
Диаграмма-шкала для визуализации теоретической и частотной вероятности
На примере парадокса Монти Холла мы смоделировали выбор человеком правильной стратегии с привлечением статистических расчетов. В общем случае:
- Стратегий может быть больше, чем две.
- Теоретические расчеты вероятности могут отсутствовать или требовать проверки. Тогда придется испытывать все стратегии и определять частотную вероятность для каждой.
- Внешне различные варианты могут никак не отличаться (двери в игре Монти Холла выглядят одинаково — визуальная симметрия).
Если поставить задачу помочь выиграть игроку, а не сбить его с толку, как на шоу, то в визуализации данных или пользовательском интерфейсе можно дополнить "двери", между которыми выбирает "игрок", диаграммами-шкалами. На такой диаграмме шкала задает градации изменения величины, и на шкалу накладывается столбик фактического значения по аналогии с термометром.
На диаграмме-шкале удобно совместить теоретическое, ожидаемое количество выигрышей (выделено серым) и фактическое после всех предыдущих игр (узкий черный столбик). Фактическое значение меняется после каждого принятого решения по выбору одной из двух стратегий и сохраняется на протяжении всей серии игр:
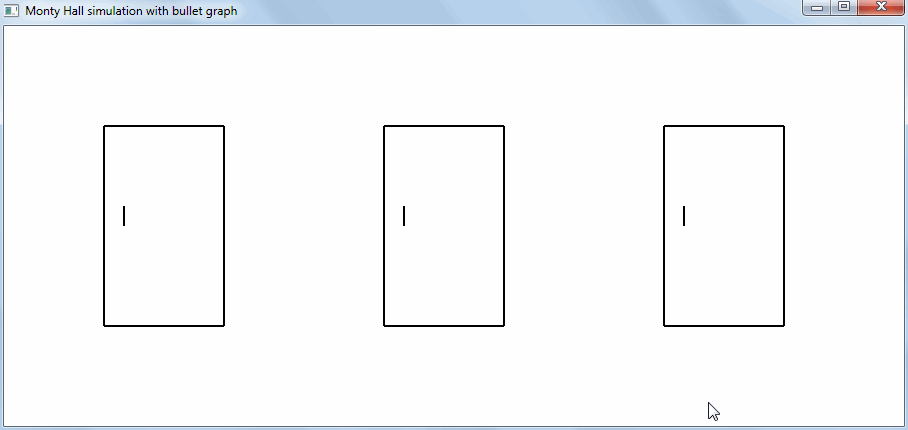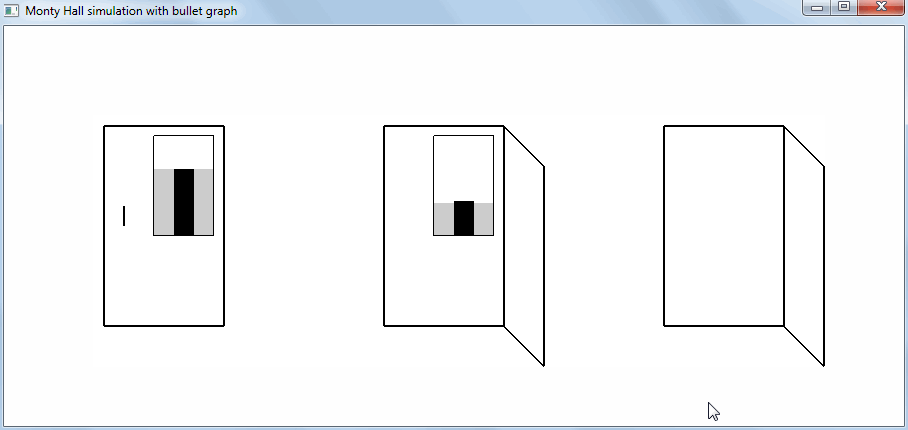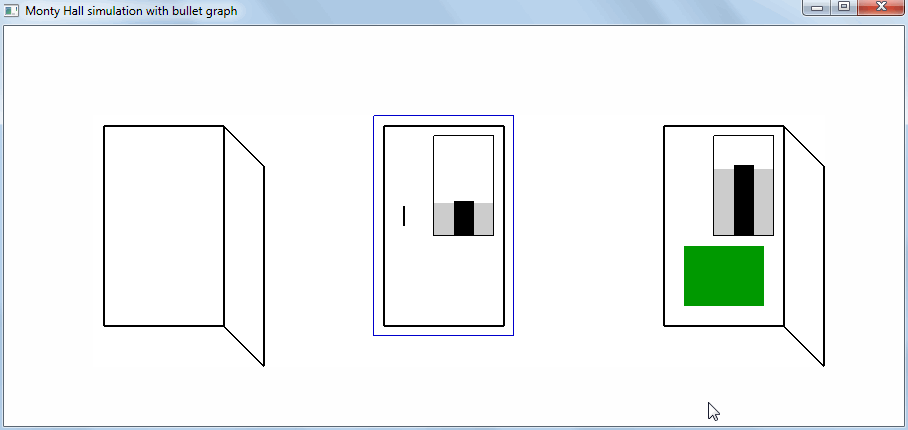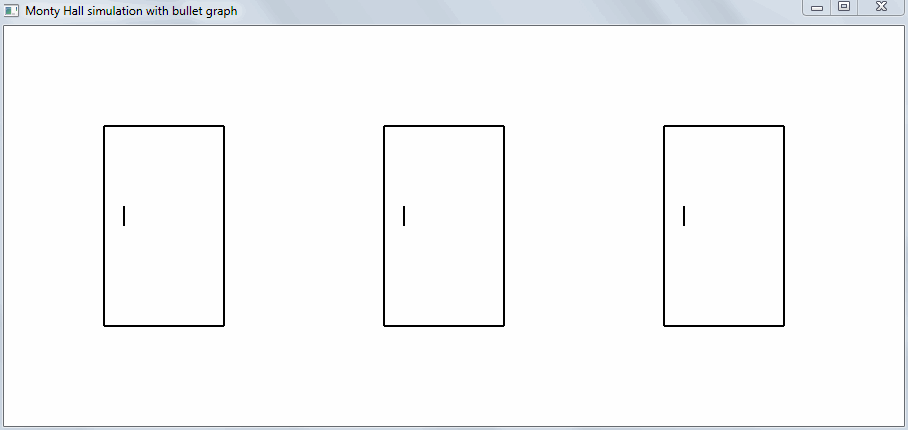
Таким образом, подходящая визуализация статистических данных помогает человеку выбрать правильную стратегию. Например, в интерфейсе, похожем на прототип, элемент интерфейса, соответствующий стратегии, может быть помечен статистическим виджетом, похожим на диаграмму-шкалу. Изображение фактических данных полезно, если пользователь выбирает между примерно одинаково успешными стратегиями. Оно позволяет ему быстро прийти к заключению:
Похоже, чаще успешно
Выводы
- Человек склонен игнорировать или неправильно использовать расчет вероятности и статистику при выборе стратегии.
- Статистику можно рассматривать как коллективную интуицию — многократные успешные исходы испытаний других людей.
- Если статистические данные корректно визуализировать, то это повысит эффективность выбора стратегии человеком.